垂线 课件

(共22张PPT)
我国跳水运动员－－－田亮
1995年世界杯双人、团体、混合团体冠军；　　1998年第13届亚运会男子10米跳台冠军；　　1999年世界杯10米跳台男子单人、双人冠军；　　1999年跳水大奖赛总决赛男子10米跳台冠军；　2000年世界杯男子10米跳台单人、双人冠军；　　2000年第27届奥运会男子10米跳台单人冠军。　　2001年世锦赛男子10米跳台单人、双人冠军；　　2001年九运会男子10米跳台冠军；　　2002年全国跳水冠军赛男子10米跳台冠军；　　2002年世界杯男子10米跳台单人、双人冠军；　　2002年全国锦标赛男子10米跳台冠军。
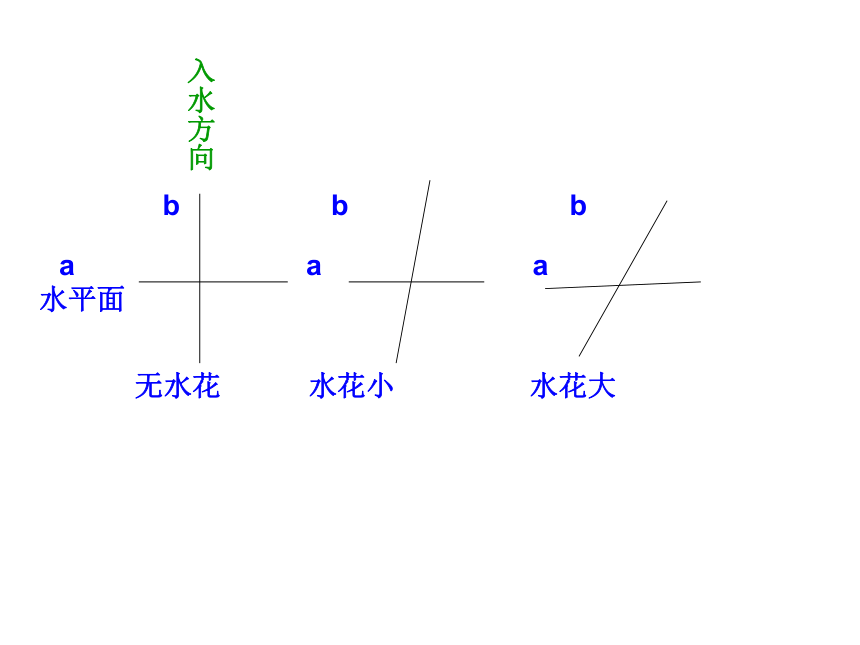
跳水运动员的入水姿势
b b b
a a a
水平面
无水花 水花小 水花大
入水方向
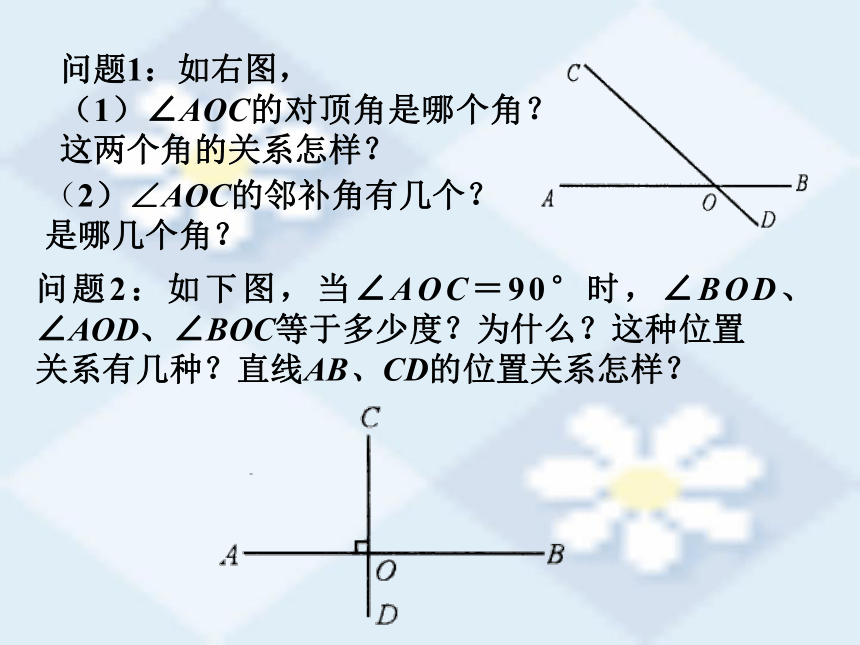
问题1：如右图，
（1）∠AOC的对顶角是哪个角？这两个角的关系怎样？
（2）∠AOC的邻补角有几个？是哪几个角？
问题2：如下图，当∠AOC＝90°时，∠BOD、∠AOD、∠BOC等于多少度？为什么？这种位置
关系有几种？直线AB、CD的位置关系怎样？
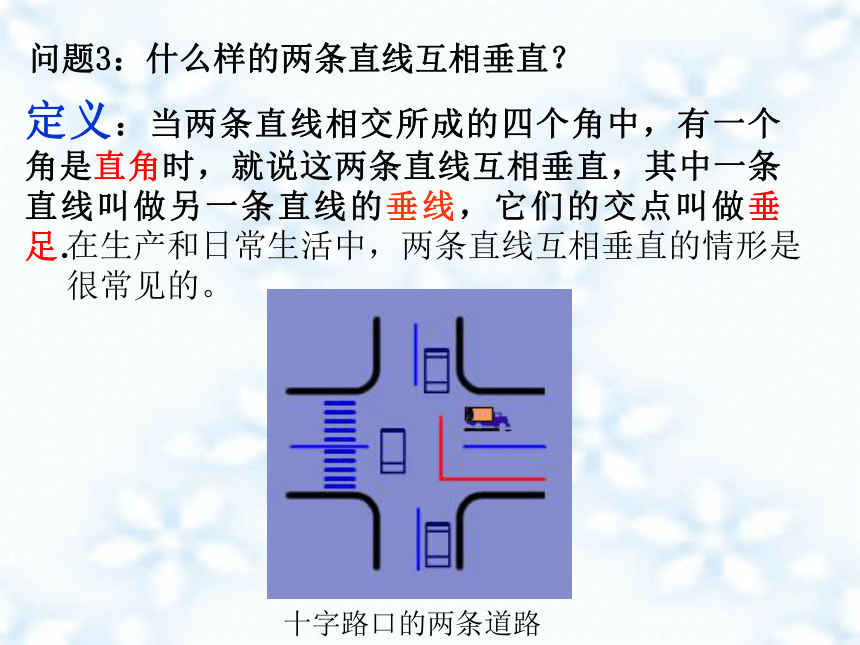
问题3：什么样的两条直线互相垂直？
定义：当两条直线相交所成的四个角中，有一个角是直角时，就说这两条直线互相垂直，其中一条直线叫做另一条直线的垂线，它们的交点叫做垂足．
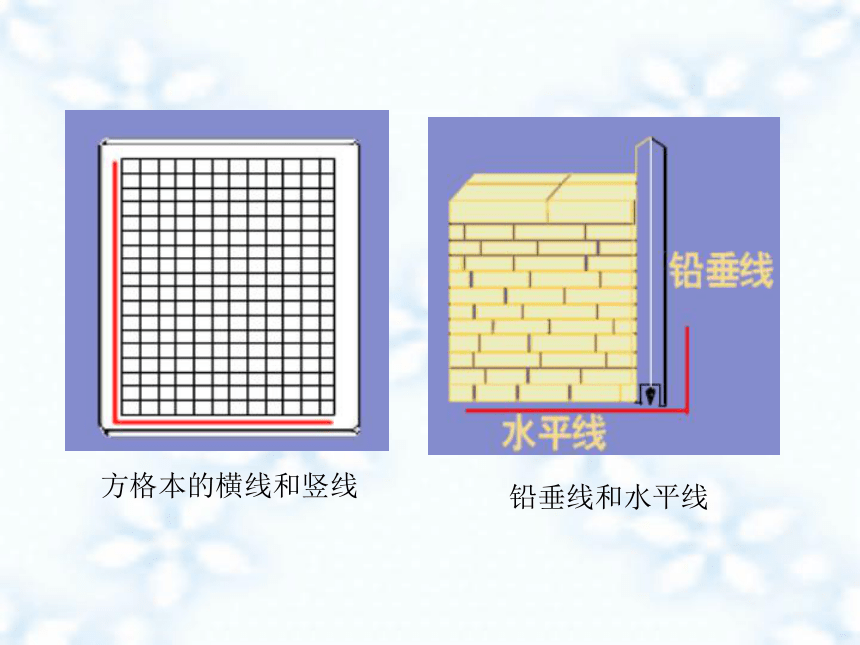
在生产和日常生活中，两条直线互相垂直的情形是很常见的。
十字路口的两条道路
方格本的横线和竖线
铅垂线和水平线
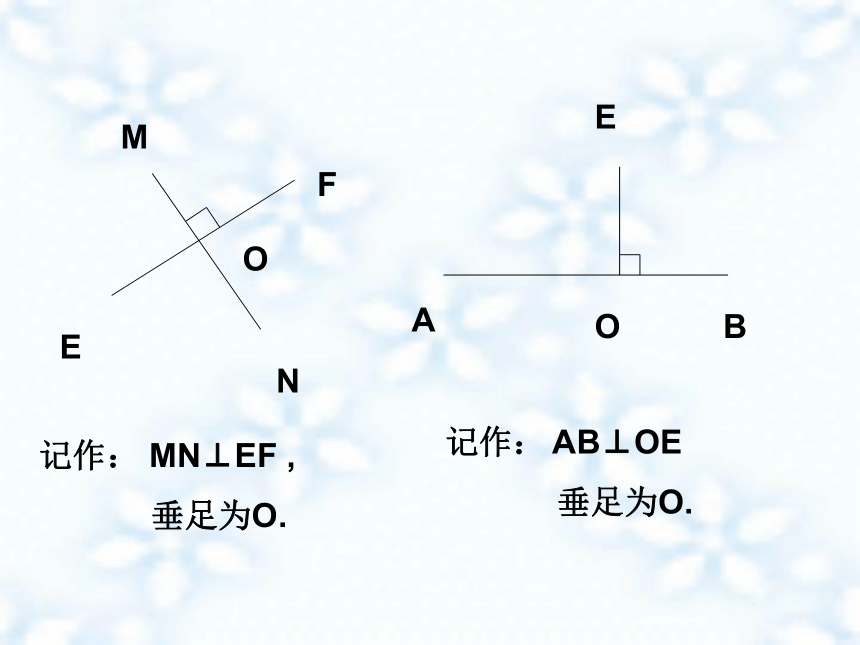
垂直的记法、读法
直线AB、CD互相垂直，记作“AB⊥CD”或
“CD⊥AB”，读作“AB垂直于CD”，如果垂足为O，
记作“AB⊥CD，垂足为O”（如图）．
E
F
M
N
O
记作： MN⊥EF ,
垂足为O.
A
B
O
E
记作： AB⊥OE
垂足为O.
垂直的定义的应用格式
∵∠AOC=90°（已知），
∴AB⊥CD（垂直的定义）．
如果直线AB、CD 相交于点O，∠AOC=90°（或三个角中的一个角等于90°），那么 AB⊥CD.
这个推理过程可以写成：
∵AB⊥CD（已知），
∴∠AOC＝90°（垂直的定义）．
如果AB⊥CD，那么所得的四个角中，必有一个是直角.这个推理过程可以写成:
选择题：
1、 两条直线相交所成的四个角中，下列条件中能判
定两条直线垂直的是
（A） 有两个角相等 （ B）有两对角相等
（C） 有三个角相等 （ D） 有四对邻补角
（C）
2、下面四种判定两条直线的垂直的方法，正确的有（ ）个
（1）两条直线相交所成的四个角中有一个角是直角，则这两条直线互相垂直
（2）两条直线相交，只有一组邻补角相等，则这两条直线互相垂直
（3）两条直线相交，所成的四个角相等，这两条直线互相垂直
（4）两条直线相交，有一组对顶角互补，则这两条直线互相垂直
（ A） 4 （B） 3
（C） 2 （D） 1
A
3、 两个角的平分线互相垂直的有（ ）
A 两角互补 B 两角互为对顶角
C 两角都是直角 D 两角互为邻补角
D
例1、如图，已知直线AB、CD都经过O点，OE为射线，
若∠1＝35° ∠2＝55°，则OE与AB的位置关系是
。
C
2 O
A B
1
E D
解：
∵∠1＝35°，∠2＝55°（已知）
垂直
∴ ∠AOE＝180°－∠1－∠2
＝ 180°－35°－55°
＝90°
∴OE⊥AB (垂直的定义)
例2：如图 ，已知AB. CD相交于O, OE⊥CD
于O,∠AOC=36°，则∠BOE= 。
（A）36° (B) 64°
(C)144° (D) 54°
A
B
O
C
D
E
54°
想一想：
（1）直线a与直线b是互相垂直的两条直
线，若直线a为已知直线，那么直线b的位置确
定吗？ 如何才能确定直线b的位置？
（2）如果过点O再画一条直线c，且直线c与直
线b不重合，能使直线c与直线a垂直吗？
（3）通过画图，你能试着总结出什么结论？
结论： 过直线上的一点有且只有一条直线与已知直线互相垂直。
（4）如果在直线a外取一点P，过点P 能画直
线a的垂线吗？能画几条？你能用量角器（或三角
尺）把它画出来吗？
（5）你能得到什么结论？
a
.
P
结论： 过直线外一点有且只有一条直线与已知
直线垂直.
结论(1)： 过直线上的一点有且只有一条直
线与已知直线互相垂直。
结论(2)： 过直线外一点有且只有一条直线与
已知直线垂直.
课堂练习
1．选择题
(1) 过点 向线段 所在直线引垂线，正确的是（ ）.
A B C D
C
课堂练习：
2. 过点P作线段或射线所在直线的垂线
A
B
.
.
.P
(1)
.
O
.P
.A
(2)
3.过点P分别向角的两边作垂线
.P
.P
.P
.P
.P
.P
两条直线相交
一般情况
垂线
对顶角：相等
邻补角：互补
垂线的存在性和唯一性
特殊情况
相交成直角