合并同类项 课件

(共16张PPT)
五练习
二、
引入
三、定义
二、
问题
一、复习
五、例2
三、练习
四、
合并
四、
练习4
六、小结
六、练习
知识点、重难点
重 点：
难 点：
知识点：
知道什么样的项是同类项
考试点：
理解同类项的概念，
掌握合并同类项的方法
同类项的概念
合并同类项
单项式：
表示数与字母的乘积的代数式叫单项式，单独一个数或一个字母也是单项式。
（注意系数的符号）
多项式：
几个单项式的和叫做多项式。
练习：指出下列单项式的系数和次数：
10x2； －abc； x ； －0.8x2y；0.74m5n
练习：说出下列多项式是几次几项式， 并指出它的每一项。
（1） 4ab－7a2b2－8ab2
（2） 5x2y－y2－x－9
复习
四次三项式
三次四项式
周末，点点一家要外出游玩，爸爸、 妈妈和点点各自选了他们要吃的东西：
买的时候，点点怎么说？
____个汉堡____个苹果____个草莓_____瓶饮料
4 3 8 3

A
B
C
x
2x
2x
2x
x
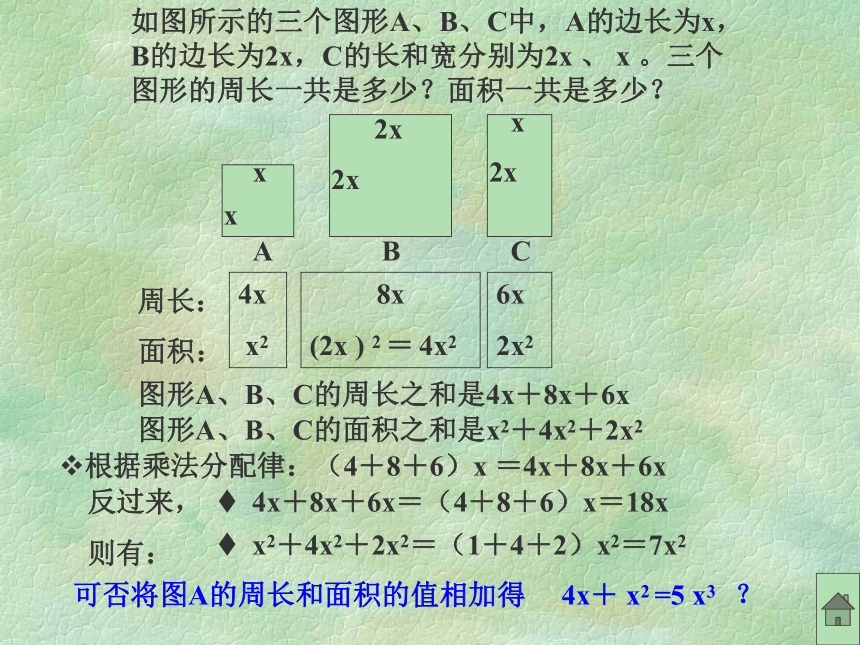
如图所示的三个图形A、B、C中，A的边长为x，B的边长为2x，C的长和宽分别为2x 、 x 。三个图形的周长一共是多少？面积一共是多少？
周长：
4x
x2
8x
(2x ) 2 ＝ 4x2
6x
2x2
图形A、B、C的周长之和是4x＋8x＋6x
图形A、B、C的面积之和是x2＋4x2＋2x2
x
根据乘法分配律：（4＋8＋6）x ＝4x＋8x＋6x
4x＋8x＋6x＝（4＋8＋6）x＝18x
反过来，
则有：
x2＋4x2＋2x2＝（1＋4＋2）x2＝7x2
可否将图A的周长和面积的值相加得 4x＋ x2 =5 x3 ？
面积：
练习1 　判断下列各组中的两项是不是同类项，并说明为什么？
（1）0.2x2y与2x2y (2)4abc与4ac
(3) 2m 2 n与2mn2 （4）－125与12
(5) 4st与5ts
4x＋8x＋6x＝（4＋8＋6）x＝18x
x2＋4x2＋2x2＝（1＋4＋2）x2＝7x2
同类项的定义：所含字母相同，并且相同字母的指数也分别相同的项，叫做同类项。几个常数项也是同类项。





4x＋ x2 ≠ 5 x3
练习2 　说出下列多项式中的同类项。
(1)5x2y－y2－x－1＋x2y＋2x－9；
练习3　　已知单项式－5x2ym与6xny3是同类项，则m＝　　　，n＝　　　，则mn＝_______。
判断同类项：1、字母相同；2、相同字母指数也 分别相同。与系数大小无关，与字母顺序无关。
—— ——
~~~ ~~~
=== ===
-— -——
3 2
===== ===== ====
32 ＝ 9
(2)4ab－7a2b2－8ab2＋5a2b2－9ab＋a2b2
4x＋8x＋6x＝（4＋8＋6）x＝18x
x2＋4x2＋2x2＝（1＋4＋2）x2＝7x2
问题：合并同类项实际上是合并什么？
——系数相加
——不改变
多项式中的几个同类项合并为一项，叫做合并同类项。
合并同类项时，同类项的系数相加的结果作为合并后的系数，字母和字母的指数不变。
例１、合并同类项：
(1)3x3＋x3 (2)xy2－５xy2 (3)－4a3b2＋4b2a3
解：
(1) 3x3＋x3＝
(3＋1)x3
＝4x3
(2) xy2－5xy2
＝(1－5)xy2
＝－4xy2
(3) －4a3b2＋4b2a3
＝(－4＋4)a3b2
＝0
字母和字母的指数有何变化？
练习4：判断对错：
（1）5 x2＋２x３＝７x５
（2）7 x2－３x＝４x
　　 （3）－３x2y＋２x2y＝－５x2y
练习５：合并同类项：
(1)5x＋4x＝　　
(2)－７ab＋6ab＝
(3) －4x ＋4x ＝　　　　
(4) x2y＋yx2＝
合并同类项时，同类项的系数相加的结果作为合并后的系数，字母和字母的指数不变。



9x
－ab
0
2x2y
＝－x2y
例2 先找出下列多项式中的同类项，然后合并同类项：
（1）4x2－8x＋5－3x2＋6x－2
解：4x2－8x＋5－3x2＋6x－2
-— ——
=== ===
~~~ ~~~
＝（4x2－3x2）＋(－8x＋6x)＋(5－2)
＝ x2－2x＋3
（2）xy2 －3y3 －3x2y＋2y3－x2y－ xy2
解： xy2 －3y3 －3x2y＋2y3－x2y－ xy2
— ——
=== ===
~~~~~ ~~~~
＝( xy2 － xy2 )＋(－3y3 ＋2y3)＋(－3x2y －x2y )
＝０－y3 －４x2y
＝ －４x2y －y3
合并同类项的步骤：
1、找出同类项；
2、结合同类项；
3、合并同类项。
练习６：合并同类项
（1）6x－10x2 －5x
（2） －2x2－2x3＋2x3－x2
（3） 0.3 xy2 －3x2y－x2y－ xy2
（4） 5y3 － 7 xy2 －5y3 －4x2y－6 xy2 －3x2y
合并同类项的步骤：
1、找出同类项
2、同类项结合
3、合并同类项。
结果按某一字母的升幂或降幂排列。
用不同的线划出各组同类项，注意每一项的符号。
用括号将同类项结合，括号间用加号连接。
合并同类项——小结：
同类项的定义：所含______，并且______的______ 也相同的项，叫做同类项。几个常数项也是_______。
判断同类项：1、字母_____；2、相同字母指数也分别_____。与______无关，与_______无关。
合并同类项的法则：_______相加，作为结果的系数，字母和字母的指数______。
思考题
如果单项式2axm y与单项式5bx 2m-3 y是关于x、y的单项式，并且它们是同类项。求：
（1）(9m-28) 2003的值；
（2）若2ax m y+5bx 2m-3 y=0,并且xy ≠ 0,求（2a+5b）2002的值。
作业：
第一册第156页习题3.2A组2、3、4题的双数题。
感谢各位老师莅临指导