第十一章 反比例函数 单元测试卷(含解析)
文档属性
| 名称 | 第十一章 反比例函数 单元测试卷(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 11:49:51 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中数学苏科版八年级下册
第十一章
反比例函数
单元测试卷
一、单选题(本题共10题,每题3分,共30分)
1.下列关系式中:①y=2x;②;③y=﹣;④y=5x+1;⑤y=x2﹣1;⑥y=;⑦xy=11,y是x的反比例函数的共有( )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
2.在函数
的图象上有三点,
,
,
,已知
,则下列各式正确的是(??
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
3.如图,点
P
是反比例函数
y
=6/x的图象上的任意一点,过点
P分别作两坐标轴的垂线,与坐标轴构成矩形
OAPB,点
D
是矩形OAPB
内任意一点,连接
DA、DB、DP、DO,则图中阴影
部分的面积(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
4.已知四边形
是矩形,边
在
轴上,边
在
轴上,反比例函数
经过矩形
对角线的交点
.若
的面积为
,则
的值是(??
)
A.?10????????????????????????????????????????B.?5????????????????????????????????????????C.?????????????????????????????????????????D.?
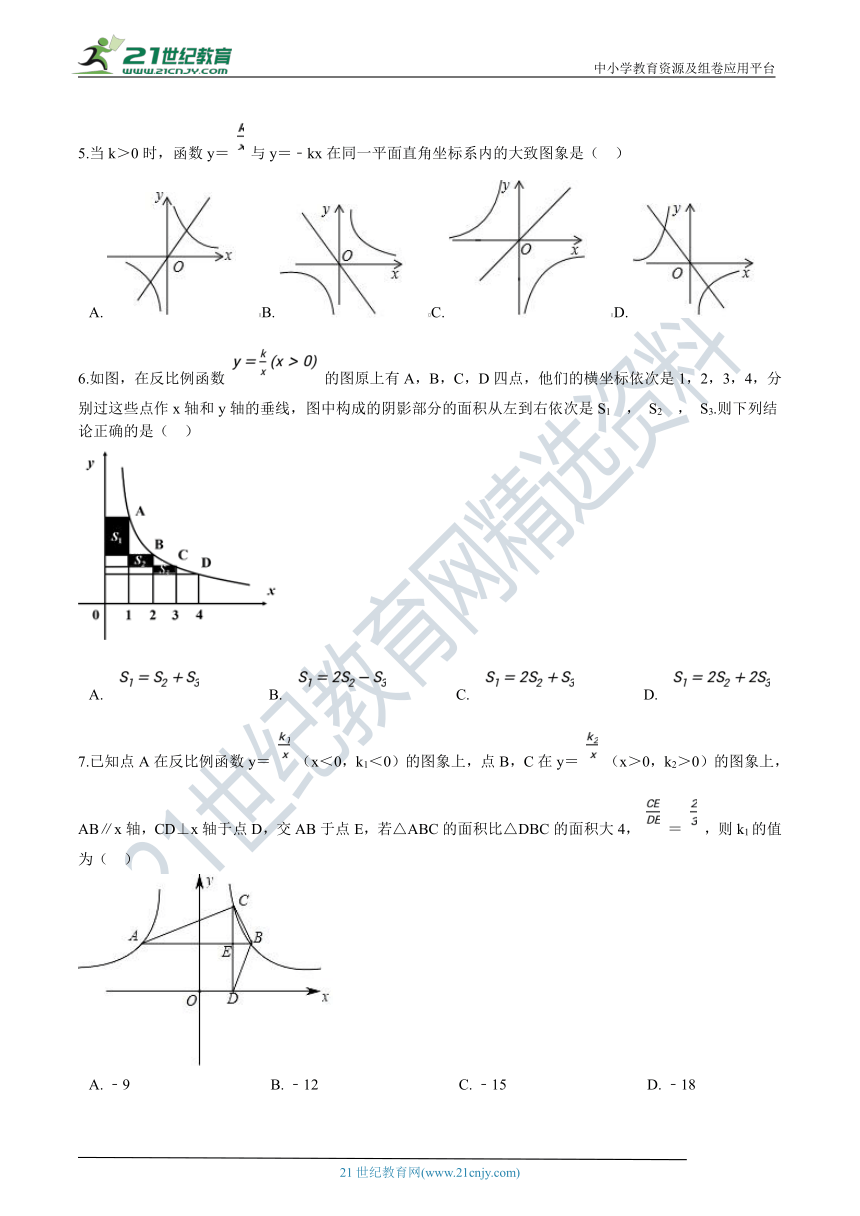
5.当k>0时,函数y=
与y=﹣kx在同一平面直角坐标系内的大致图象是(??
)
A.???????B.???????C.???????D.?
6.如图,在反比例函数
的图原上有A,B,C,D四点,他们的横坐标依次是1,2,3,4,分别过这些点作x轴和y轴的垂线,图中构成的阴影部分的面积从左到右依次是S1
,
S2
,
S3.则下列结论正确的是(??
)
A.???????????????????B.???????????????????C.???????????????????D.?
7.已知点A在反比例函数y=
(x<0,k1<0)的图象上,点B,C在y=
(x>0,k2>0)的图象上,AB∥x轴,CD⊥x轴于点D,交AB于点E,若△ABC的面积比△DBC的面积大4,
=
,则k1的值为(??
)
A.?﹣9?????????????????????????????????????B.?﹣12?????????????????????????????????????C.?﹣15?????????????????????????????????????D.?﹣18
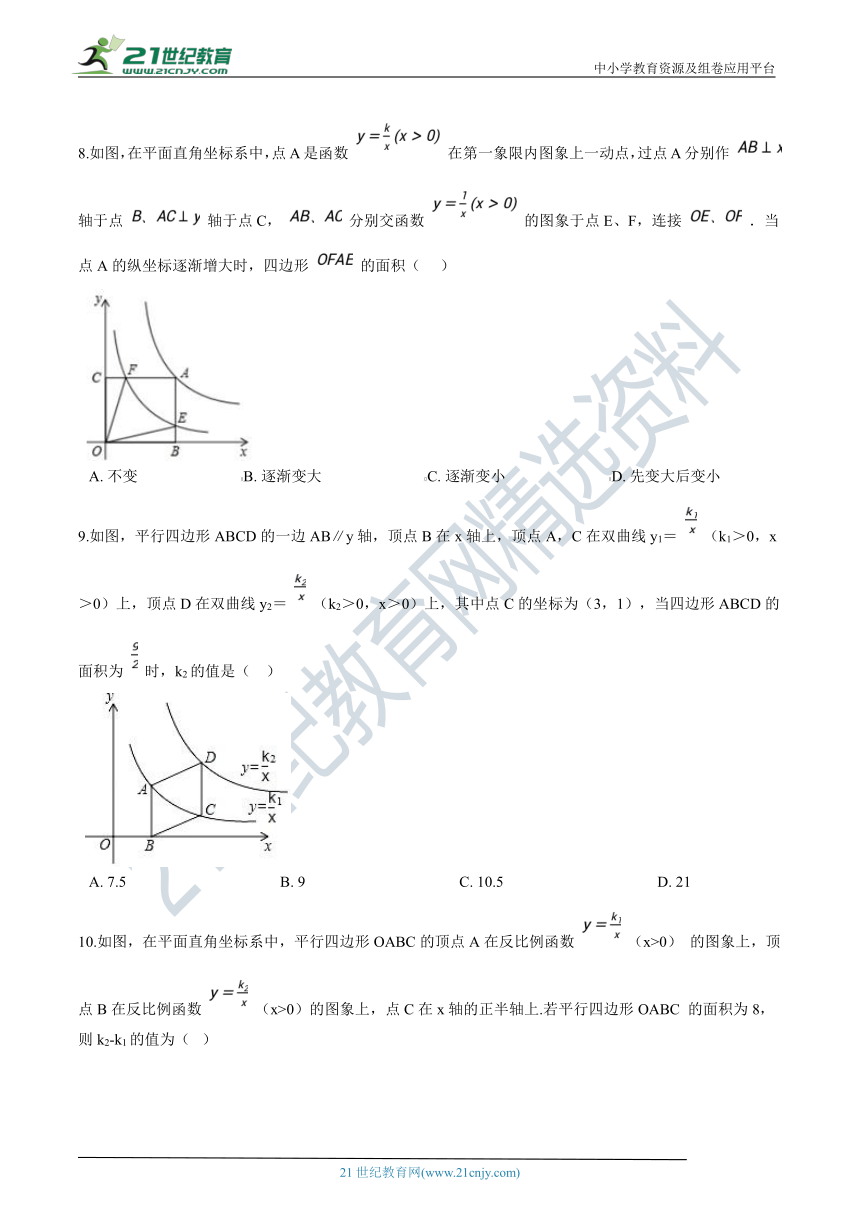
8.如图,在平面直角坐标系中,点A是函数
在第一象限内图象上一动点,过点A分别作
轴于点
轴于点C,
分别交函数
的图象于点E、F,连接
.当点A的纵坐标逐渐增大时,四边形
的面积(???
)
A.?不变???????????????????????????B.?逐渐变大???????????????????????????C.?逐渐变小???????????????????????????D.?先变大后变小
9.如图,平行四边形ABCD的一边AB∥y轴,顶点B在x轴上,顶点A,C在双曲线y1=
(k1>0,x>0)上,顶点D在双曲线y2=
(k2>0,x>0)上,其中点C的坐标为(3,1),当四边形ABCD的面积为
时,k2的值是(??
)
A.?7.5????????????????????????????????????????B.?9????????????????????????????????????????C.?10.5????????????????????????????????????????D.?21
10.如图,在平面直角坐标系中,平行四边形OABC的顶点A在反比例函数
(x>0)
的图象上,顶点B在反比例函数
(x>0)的图象上,点C在x轴的正半轴上.若平行四边形OABC
的面积为8,则k2-k1的值为(?
)
A.?4??????????????????????????????????????????B.?8??????????????????????????????????????????C.?12??????????????????????????????????????????D.?16
二、填空题(本题共8题,每题2分,共16分)
11.如果反比例函数y=
的图象位于第二、四象限,那么满足条件的正整数k的值是________.
12.已知反比例函数
,当
时,x的取值范围是________.
13.已知一次函数y1=k1x+b(k1
,
b为常数)与反比例函数y2=
(k2为常数),函数y1、y2与自变量x的部分对应值分别如表1、表2所示:
则关于x的不等式k1x+b<
的解集是________.
14.如图,在平面直角坐标系中,菱形
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的图象上,点D的坐标为
.将菱形ABCD沿x轴正方向平移________个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
15.如图,在平面直角坐标系中,一次函数
和函数
的图象交于A、B两点.利用函数图象直接写出不等式
的解集是________.
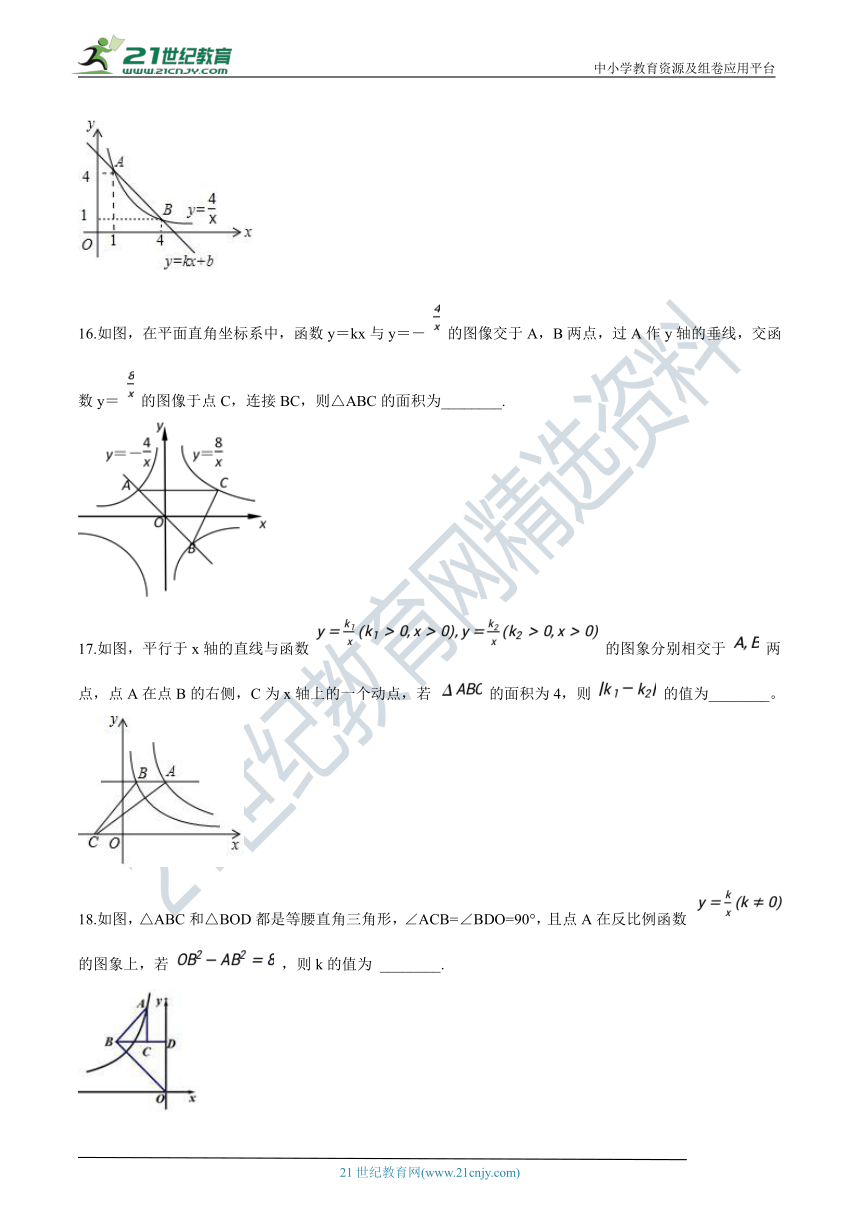
16.如图,在平面直角坐标系中,函数y=kx与y=-
的图像交于A,B两点,过A作y轴的垂线,交函数y=
的图像于点C,连接BC,则△ABC的面积为________.
17.如图,平行于x轴的直线与函数
的图象分别相交于
两点,点A在点B的右侧,C为x轴上的一个动点,若
的面积为4,则
的值为________。
18.如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数
的图象上,若
,则k的值为
________.
三、综合题(本题共10题,共84分)
19.如反比例函数的图像经过点
,点
也在反比例函数图像上.
(1)求反比例函数的解析式;
(2)求
、
两点间的距离.
20.
在直角坐标系内的位置如图所示,
,反比例函数
在第一象限内的图像与
交于点
与
交于点
.
(1)求该反比例函数的解析式及图像为直线
的正比例函数解析式;
(2)求
的长.
21.如图,一次函数y=x+6的图象与反比例函数y
(x<0)的图象交于A(﹣1,a)、B(b,1)两点.
(1)求a、b、k的值;
(2)当一次函数的值大于反比例函数的值时,根据图象写出自变量x的取值范围;
(3)求△ABO的面积.
22.如图,一次函数y1=k1x+b与反比例函数
的图象相交于点A(1,﹣4)和点B(﹣2,m).
(1)分别求这两个函数的表达式;
(2)连接AO,BO.求△AOB的面积;
(3)若y2>y1>0,请直接写出满足条件的自变最x的取值范围.
23.如图,点A是反比例函数y=
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.
24.如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线
在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)
?
(1)求m和n的值;
(2)过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线
交于点P、Q,求△APQ的面积.
(3)直接写出
的解集
(4)直接写出直方程
的解。
25.已知,反比例函数
的图象过第二象限内的点
,
轴于
,
面积为3,若直线
经过点
,并且经过反比例函数
的图象上另一点
.
(1)求反比例函数的解析式;
(2)求直线
解析式
(3)求
的面积;
(4)直接写出不等式
的解集.
26.为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与药物在空气中的持续时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.根据以上信息解答下列问题:
(1)分别求出药物燃烧时及燃烧后y关于x的函数表达式.
(2)当每立方米空气中的含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于3.2mg的持续时间超过20分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
27.已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数
,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式.
28.如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD
,
过点E作双曲线交线段BC于点F
,
作CD中点M
,
连接BE、EF、EM、FM
.
(1)当t=1时,求点F的坐标.
(2)若BE平分∠AEF
,
则t的值为多少?
(3)若∠EMF为直角,则t的值为多少?
答案解析部分
一、单选题
1.【答案】
C
解:①y=2x是正比例函数;
②可化为y=5x,是正比例函数;
③y=﹣符合反比例函数的定义,是反比例函数;
④y=5x+1是一次函数;
⑤y=x2﹣1是二次函数;
⑥y=不是函数;
⑦xy=11可化为y=
,
符合反比例函数的定义,是反比例函数.
故选C.
2.【答案】
A
解:
图象在第一、三象限,在每个象限内,y随x的增大而减小
故答案为:A.
3.【答案】
C
解:P是反比例函数
的图象的任意点,过点P分别做两坐标轴的垂线,∴与坐标轴构成矩形OAPB的面积=6.∴阴影部分的面积=
×矩形OAPB的面积=3.
4.【答案】
A
解:设双曲线
上E点的坐标是(x,y),
∵E是矩形
对角线的交点,
∴CE=OE
∴OC=2y,
中OC上的高=x
∵
的面积为
,
∴
=10,xy=10
所以k=10
故答案为:A
5.【答案】
B
解:∵k>0,
∴函数
的图象在第一、三象限,
函数
的图象在第二、四象限且经过原点,
故答案为:B.
6.【答案】
D
解:∵S1=1×(
)=
;
S2=1×(
)=
;
S3=1×(
)=
;
∴S1=2S2+2S3.
故答案为:D.
7.【答案】
B
解:设CE=2t,则DE=3t,
∵点B,C在y=
(x>0,k2>0)的图象上,AB∥x轴,CD⊥x轴,
∴C(
,5t),B(
,3t),
∴A(
,3t),
∵△ABC与△DBC的面积之差为4,
∴
×(
﹣
)×2t﹣
×5t(
﹣
)=4,
∴k1=﹣12.
故答案为:B.
8.【答案】
A
解:∵点A是函数
)在第一象限内图象上,过点A分别作AB⊥x轴于点B,AC⊥y轴于点C,
∴矩形ACOB的面积为k,
∵点E、F在函数
的图象上,
∴
?
,
∴四边形OFAE的面积
,
故四边形OFAE的面积为定值
,保持不变,
故答案为:A.
9.【答案】
C
解:∵C(3,1)在双曲线y1=
(k1>0,x>0)上,
∴k1=3×1=3,
∴y1=
,
设A(m,
),
∵平行四边形ABCD的面积为
,
∴(3﹣m)?
=
,
解得m=
,
∴A(
,
),
∵平行四边形ABCD的一边AB∥y轴,顶点B在x轴上,
∴D(3,
),
∵点D在双曲线y2=
(k2>0,x>0)上,
∴k2=3×
=10.5,
故答案为:C.
10.【答案】
B
解:∵A,B分别在
和
的图象上,且A,B的纵坐标相同
∴设
∴
化简得:
故答案选:B
二、填空题
11.【答案】
1,2
解:本题考查的是反比例函数的图象的性质
由反比例函数的性质列出不等式,解出k的范围,在这个范围写出k的整数解则可.
由题意得k-3<0,k<3,则满足该条件的正整数k的值是1,2.
12.【答案】
x<0或x>3
解:
反比例函数??
,
当??时
,<2且x≠0,
若x>0,则2x>6,∴x>3,
若x<0,则2x<6,∴x<3,∴x<0,
综上所述:
x<0或x>3
13.【答案】
x<―2或0<x<3
解:把x=-2,y=-3和x=0,y=-1代入一次函数的解析式y1=k1x+b得,
,
解得,
,
∴一次函数的解析式为:y1=x-1;
把x=3,y=2代入反比例函数的解析式y2=
中得,
k=6,
∴反比例函数的解析式为:y2=
,
联立方程组
,
解得:
或
,
∴直线y1=x-1与双曲线y2=
的交点为:
(-2,-3)或(3,2),
作出草图如下:
由函数图象可知,当双曲线在直线上方时,x<-2或0<x<3,
∴关于x的不等式k1x+b<
的解集是:x<-2或0<x<3,
故答案为:x<-2或0<x<3.
14.【答案】
或
解:因为D
,勾股定理知,所以OD
=
=4,
所以A(
,7),所以反比例函数是y=
,
当D点移动到函数上时,纵坐标恰好和D相同,则3=
,x=
,所以移动了
个单位,
当B点移动到函数上时,B(0,4),4=
,x=
,所以移动了
个单位.
故答案为
或
.
15.【答案】
1<x<4
解:不等式
的解集实际上是反比例函数值小于一次函数值的自变量x的取值范围,根据图象得:1<x<4.
故答案为:1<x<4.
16.【答案】
12
解:如图,连接OC设AC交y轴于E.
∵AC⊥y轴于E,
∴S△AOE=2,S△OEC=4,
∴S△AOC=6,
∵A,B关于原点对称,
∴OA=OB,
∴S△ABC=2S△AOC=12,
故答案为:12.
17.【答案】
8
解:设:A、B、C三点的坐标分别是A(
,m)、B(
,m),
则:△ABC的面积=
?AB?yA=
?(
-
)?m=4,
则|k1-k2|=8.
故答案为8.
18.【答案】
-4
解:设A点坐标为(a,b),
∵△ABC和△BOD都是等腰直角三角形,
∴AB=
AC,OB=
BD,BC=AC,OD=BD
∵OB2-AB2=8,
∴2OD2-2AC2=8,即OD2-AC2=4,
∴(OD+AC)(OD-AC)=4,
又∵因为a<0,b>0,
∴a?b=-4
∴k=-4.
三、综合题
19.【答案】
(1)解:设反比例函数为:
∵反比例函数的图像经过点
∴
∴
∴反比例函数为:
;
(2)解:∵点
也在反比例函数图像上
∴
∴
∵
时,
∴
是
的解
∴
∴
、
两点间的距离
.
20.【答案】
(1)解:将点
代入反比例函数解析式中,得
解得:k=8
∴反比例函数解析式为
将点
代入反比例函数解析式中,得
解得:m=2
∴点
设直线OB的正比例函数解析式为y=ax
将点
代入,得
2=4a
解得:a=
∴直线OB的解析式为y=
x;
(2)解:∵
即
轴
∴点B的横坐标等于点C的横坐标8
将x=8代入y=
x中,解得y=4
∴点B的坐标为(8,4)
∴AB=4
∵点
∴AC=1
∴BC=AB-AC=3
21.【答案】
(1)解:把A(﹣1,a)代入y=x+6
得a=﹣1+6=5,
∴A(﹣1,5),
把B(b,1)代入y=x+6
得b+6=1,
解得:b=﹣5,
把A(﹣1,5)代入y
得k=﹣1×5=﹣5;
(2)解:∵A(﹣1,5),B(﹣5,1),
∴当一次函数的值大于反比例函数的值时,自变量x的取值范围为﹣5<x<﹣1;
(3)解:设直线y=x+6与x轴交于点C,连接OA,OB,如图,
则C(﹣6,0),
∴S△OAB=S△OAC﹣S△BOC
6×5
6×1
=12.
22.【答案】
(1)解:把点A(1,﹣4)的坐标代入y=
,得﹣4=
,求得k2=﹣4,
∴反比例函数y2=﹣
;
把点B(﹣2,m)的坐标代入y=﹣
,得m=﹣
=2
∴点B的坐标为(﹣2,2)
把点A(1,﹣4)、B(﹣2,2)分别代入y1=k1x+b,得
,
解得
,
∴一次函数y1=﹣2x﹣2;
(2)解:如图,
在一次函数y1=﹣2x﹣2中,令x=0,则y=﹣2,
∴直线AB与y轴的交点为E(0,﹣2),
∴S△AOB=S△AOE+S△BOE=
=3;
(3)解:由图象可知:y2>y1>0时,自变最x的取值范围是﹣2<x<0.
解:(3)∵点A(1,-4),点B(-2,2)
由题意可知:当﹣2<x<0时,
y2>y1>0
23.【答案】
(1)解:当x=n时,y=
,∴A(n,
),
由题意知BD是AC的中垂线,∴点B的纵坐标为
,
∴把y=
代入y=
得x=2n,∴B(2n,
)
(2)解:由(1)可知AM=CM,BM=MD=
,
∴四边形ABCD是平行四边形,
又∵BD⊥AC,∴平行四边形ABCD是菱形
(3)解:当四边形ABCD是正方形时,△ABM为等腰直角三角形,
∵△ABM的面积为2,∴AM=BM=2,∴A(-2,4),B(-4,2),
由此可得直线AB所对应的函数表达式为y=x+6.
24.【答案】
(1)解:把C点坐标代入反比例函数中得
?
解得m=4
在把C(1,4)代入一次函数中得
?
解得n=2
(2)解:由(1)知一次函数和反比例函数的解析式为
和
则A点坐标为(-1,0)
AD=4
把x=3分别代入得
y=8和y=
则P点坐标为(3,5),Q点坐标为(3,
)
则PQ=
△APQ的面积=
=
=
(3)解:
<0可以看成
函数y=kx+b的图像在
图像的下方时x的取值范围
由图像得Q点的右边和C点的左边时,
y=kx+b的图像在
的下方,
即x<1或者x>3.
(4)x=1或x=3
解:(4)由图像知在C点和Q点时
y=kx+b和
相交,
所以
=0的解为x=1或x=3.
25.【答案】
(1)解:∵
面积为3,
,
∴
,即
,
∴
,
∵反比例函数为
过点
,
∴
,即反比例函数为:
,
∵反比例函数为
,
(2)解:∵点
在反比例函数
上,
∴
∴
.
.
∵直线
经过点
∴
解得:
线
的解析式为:
.
(3)解:连OC,
∴M点的坐标为(2,0),
∴S△AOC=S△AOM+S△COM=
×2×3+
×2×
=
;
(4)解:如图,
∵点A(-2,3),点O(0,0)
当x≤-2时,
,
当-2≤x<0时,;
∵点B(4,),点O(0,0)
∴当0<x≤4时
,
当x>4时,;
∴不等式
的解集是x≤?2或0<x≤4.
26.【答案】
(1)解:y=
x(0≤x≤10)
y=
?(x≥10)
(2)解:把y=1.6代入y=
x可得x=2
把y=1.6
代入y=
可得x=50
根据图象,当y≥1.6时,2≤x≤50
即从消毒开始后的第2分至50分内消毒人员不可以留在教室里.
(3)解:把y=3.2代入y=
x可得x=4
把y=3.2代入y=
可得x=25
∵25-4>20
∴本次消毒有效
27.【答案】
(1)解:如图1,当点A在x轴正半轴,点B在y轴负半轴上时,
∵OC=OD=1,
∴正方形ABCD的边长CD=
;
∵当点A在x轴负半轴、点B在y轴正半轴上时,
∴设正方形的边长为a,
∴3a=CD=
.
∴a=
,
∴正方形边长为
,
∴一次函数y=x+1图象的伴侣正方形的边长为
或
;
(2)解:如图2,作DE,CF分别垂直于x、y轴,
∵AB=AD=BC,∠DAE=∠OBA=∠FCB,
∴△ADE≌△BAO≌△CBF.
∵m<2,
∴DE=OA=BF=m,OB=CF=AE=2﹣m,
∴OF=BF+OB=2,
∴C点坐标为(2﹣m,2),
设反比例函数的解析式为:
,
∵D(2,m),C(2﹣m,2)
∴
,
∴由②得:k=2m③,
∴把k=2m代入①得:2m=2(2﹣m),
∴解得m=1,k=2,
∴反比例函数的解析式为y=
.
28.【答案】
(1)t=1时,E点坐标为(1,2),F点横坐标x=2,
设经过E的双曲线为?
,
把E点坐标代入得:
,
再把F点横坐标x=2代入
,
得y=1,所以F点坐标为(2,1).
(2)因为A点坐标为(1,0),G点坐标为(1,1),
则t秒后,E点坐标可以表示为(1,1+t),
B点坐标可以表示为(1+t,0),
设经过E点双曲线为:
,
把E点坐标代入得:
,
F点也在双曲线上,F点横坐标和B相同,
把x=1+t代入函数
得,
y=1,所以F点坐标为(1+t,1),
因为AE
BC,所以
,
又EB平分
,所以
,
EF=BF,
即
,
解得t=
.
(3)因为D点坐标为(1,3),M为DC中点,则M点坐标为(1,
),
又
是直角,所以
是直角三角形,
由勾股定理
,
得:
,
解得t=
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
初中数学苏科版八年级下册
第十一章
反比例函数
单元测试卷
一、单选题(本题共10题,每题3分,共30分)
1.下列关系式中:①y=2x;②;③y=﹣;④y=5x+1;⑤y=x2﹣1;⑥y=;⑦xy=11,y是x的反比例函数的共有( )
A.?4个???????????????????????????????????????B.?3个???????????????????????????????????????C.?2个???????????????????????????????????????D.?1个
2.在函数
的图象上有三点,
,
,
,已知
,则下列各式正确的是(??
)
A.??????????????????????B.??????????????????????C.??????????????????????D.?
3.如图,点
P
是反比例函数
y
=6/x的图象上的任意一点,过点
P分别作两坐标轴的垂线,与坐标轴构成矩形
OAPB,点
D
是矩形OAPB
内任意一点,连接
DA、DB、DP、DO,则图中阴影
部分的面积(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
4.已知四边形
是矩形,边
在
轴上,边
在
轴上,反比例函数
经过矩形
对角线的交点
.若
的面积为
,则
的值是(??
)
A.?10????????????????????????????????????????B.?5????????????????????????????????????????C.?????????????????????????????????????????D.?
5.当k>0时,函数y=
与y=﹣kx在同一平面直角坐标系内的大致图象是(??
)
A.???????B.???????C.???????D.?
6.如图,在反比例函数
的图原上有A,B,C,D四点,他们的横坐标依次是1,2,3,4,分别过这些点作x轴和y轴的垂线,图中构成的阴影部分的面积从左到右依次是S1
,
S2
,
S3.则下列结论正确的是(??
)
A.???????????????????B.???????????????????C.???????????????????D.?
7.已知点A在反比例函数y=
(x<0,k1<0)的图象上,点B,C在y=
(x>0,k2>0)的图象上,AB∥x轴,CD⊥x轴于点D,交AB于点E,若△ABC的面积比△DBC的面积大4,
=
,则k1的值为(??
)
A.?﹣9?????????????????????????????????????B.?﹣12?????????????????????????????????????C.?﹣15?????????????????????????????????????D.?﹣18
8.如图,在平面直角坐标系中,点A是函数
在第一象限内图象上一动点,过点A分别作
轴于点
轴于点C,
分别交函数
的图象于点E、F,连接
.当点A的纵坐标逐渐增大时,四边形
的面积(???
)
A.?不变???????????????????????????B.?逐渐变大???????????????????????????C.?逐渐变小???????????????????????????D.?先变大后变小
9.如图,平行四边形ABCD的一边AB∥y轴,顶点B在x轴上,顶点A,C在双曲线y1=
(k1>0,x>0)上,顶点D在双曲线y2=
(k2>0,x>0)上,其中点C的坐标为(3,1),当四边形ABCD的面积为
时,k2的值是(??
)
A.?7.5????????????????????????????????????????B.?9????????????????????????????????????????C.?10.5????????????????????????????????????????D.?21
10.如图,在平面直角坐标系中,平行四边形OABC的顶点A在反比例函数
(x>0)
的图象上,顶点B在反比例函数
(x>0)的图象上,点C在x轴的正半轴上.若平行四边形OABC
的面积为8,则k2-k1的值为(?
)
A.?4??????????????????????????????????????????B.?8??????????????????????????????????????????C.?12??????????????????????????????????????????D.?16
二、填空题(本题共8题,每题2分,共16分)
11.如果反比例函数y=
的图象位于第二、四象限,那么满足条件的正整数k的值是________.
12.已知反比例函数
,当
时,x的取值范围是________.
13.已知一次函数y1=k1x+b(k1
,
b为常数)与反比例函数y2=
(k2为常数),函数y1、y2与自变量x的部分对应值分别如表1、表2所示:
则关于x的不等式k1x+b<
的解集是________.
14.如图,在平面直角坐标系中,菱形
的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数
的图象上,点D的坐标为
.将菱形ABCD沿x轴正方向平移________个单位,可以使菱形的另一个顶点恰好落在该函数图象上.
15.如图,在平面直角坐标系中,一次函数
和函数
的图象交于A、B两点.利用函数图象直接写出不等式
的解集是________.
16.如图,在平面直角坐标系中,函数y=kx与y=-
的图像交于A,B两点,过A作y轴的垂线,交函数y=
的图像于点C,连接BC,则△ABC的面积为________.
17.如图,平行于x轴的直线与函数
的图象分别相交于
两点,点A在点B的右侧,C为x轴上的一个动点,若
的面积为4,则
的值为________。
18.如图,△ABC和△BOD都是等腰直角三角形,∠ACB=∠BDO=90°,且点A在反比例函数
的图象上,若
,则k的值为
________.
三、综合题(本题共10题,共84分)
19.如反比例函数的图像经过点
,点
也在反比例函数图像上.
(1)求反比例函数的解析式;
(2)求
、
两点间的距离.
20.
在直角坐标系内的位置如图所示,
,反比例函数
在第一象限内的图像与
交于点
与
交于点
.
(1)求该反比例函数的解析式及图像为直线
的正比例函数解析式;
(2)求
的长.
21.如图,一次函数y=x+6的图象与反比例函数y
(x<0)的图象交于A(﹣1,a)、B(b,1)两点.
(1)求a、b、k的值;
(2)当一次函数的值大于反比例函数的值时,根据图象写出自变量x的取值范围;
(3)求△ABO的面积.
22.如图,一次函数y1=k1x+b与反比例函数
的图象相交于点A(1,﹣4)和点B(﹣2,m).
(1)分别求这两个函数的表达式;
(2)连接AO,BO.求△AOB的面积;
(3)若y2>y1>0,请直接写出满足条件的自变最x的取值范围.
23.如图,点A是反比例函数y=
(m<0)位于第二象限的图像上的一个动点,过点A作AC⊥x
轴于点C;M为是线段AC的中点,过点M作AC的垂线,与反比例函数的图像及y轴分别交于B、
D两点.顺次连接A、B、C、D.设点A的横坐标为n.
(1)求点B的坐标(用含有m、n的代数式表示);
(2)求证:四边形ABCD是菱形;
(3)若△ABM的面积为2,当四边形ABCD是正方形时,求直线AB的函数表达式.
24.如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线
在第一象限内交于点C(1,m),直线CQ的解析式为:y=kx+b(k≠0)
?
(1)求m和n的值;
(2)过x轴上的点D(3,0)作平行于y轴的直线l,分别与直线AB和双曲线
交于点P、Q,求△APQ的面积.
(3)直接写出
的解集
(4)直接写出直方程
的解。
25.已知,反比例函数
的图象过第二象限内的点
,
轴于
,
面积为3,若直线
经过点
,并且经过反比例函数
的图象上另一点
.
(1)求反比例函数的解析式;
(2)求直线
解析式
(3)求
的面积;
(4)直接写出不等式
的解集.
26.为预防传染病,某校定期对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(mg)与药物在空气中的持续时间x(min)成正比例;燃烧后,y与x成反比例(如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8mg.根据以上信息解答下列问题:
(1)分别求出药物燃烧时及燃烧后y关于x的函数表达式.
(2)当每立方米空气中的含药量低于1.6mg时,对人体方能无毒害作用,那么从消毒开始,在哪个时段消毒人员不能停留在教室里?
(3)当室内空气中的含药量每立方米不低于3.2mg的持续时间超过20分钟,才能有效杀灭某种传染病毒.试判断此次消毒是否有效,并说明理由.
27.已知点A、B分别是x轴、y轴上的动点,点C、D是某个函数图象上的点,当四边形ABCD(A、B、C、D各点依次排列)为正方形时,称这个正方形为此函数图象的伴侣正方形.例如:如图,正方形ABCD是一次函数y=x+1图象的其中一个伴侣正方形.
(1)若某函数是一次函数y=x+1,求它的图象的所有伴侣正方形的边长;
(2)若某函数是反比例函数
,它的图象的伴侣正方形为ABCD,点D(2,m)(m<2)在反比例函数图象上,求m的值及反比例函数解析式.
28.如图,在平面直角坐标系第一象限中,已知点A坐标为(1,0),点D坐标为(1,3),点G坐标为(1,1),动点E从点G出发,以每秒1个单位长度的速度匀速向点D方向运动,与此同时,x轴上动点B从点A出发,以相同的速度向右运动,两动点运动时间为t(0<t<2),以AD、AB分别为边作矩形ABCD
,
过点E作双曲线交线段BC于点F
,
作CD中点M
,
连接BE、EF、EM、FM
.
(1)当t=1时,求点F的坐标.
(2)若BE平分∠AEF
,
则t的值为多少?
(3)若∠EMF为直角,则t的值为多少?
答案解析部分
一、单选题
1.【答案】
C
解:①y=2x是正比例函数;
②可化为y=5x,是正比例函数;
③y=﹣符合反比例函数的定义,是反比例函数;
④y=5x+1是一次函数;
⑤y=x2﹣1是二次函数;
⑥y=不是函数;
⑦xy=11可化为y=
,
符合反比例函数的定义,是反比例函数.
故选C.
2.【答案】
A
解:
图象在第一、三象限,在每个象限内,y随x的增大而减小
故答案为:A.
3.【答案】
C
解:P是反比例函数
的图象的任意点,过点P分别做两坐标轴的垂线,∴与坐标轴构成矩形OAPB的面积=6.∴阴影部分的面积=
×矩形OAPB的面积=3.
4.【答案】
A
解:设双曲线
上E点的坐标是(x,y),
∵E是矩形
对角线的交点,
∴CE=OE
∴OC=2y,
中OC上的高=x
∵
的面积为
,
∴
=10,xy=10
所以k=10
故答案为:A
5.【答案】
B
解:∵k>0,
∴函数
的图象在第一、三象限,
函数
的图象在第二、四象限且经过原点,
故答案为:B.
6.【答案】
D
解:∵S1=1×(
)=
;
S2=1×(
)=
;
S3=1×(
)=
;
∴S1=2S2+2S3.
故答案为:D.
7.【答案】
B
解:设CE=2t,则DE=3t,
∵点B,C在y=
(x>0,k2>0)的图象上,AB∥x轴,CD⊥x轴,
∴C(
,5t),B(
,3t),
∴A(
,3t),
∵△ABC与△DBC的面积之差为4,
∴
×(
﹣
)×2t﹣
×5t(
﹣
)=4,
∴k1=﹣12.
故答案为:B.
8.【答案】
A
解:∵点A是函数
)在第一象限内图象上,过点A分别作AB⊥x轴于点B,AC⊥y轴于点C,
∴矩形ACOB的面积为k,
∵点E、F在函数
的图象上,
∴
?
,
∴四边形OFAE的面积
,
故四边形OFAE的面积为定值
,保持不变,
故答案为:A.
9.【答案】
C
解:∵C(3,1)在双曲线y1=
(k1>0,x>0)上,
∴k1=3×1=3,
∴y1=
,
设A(m,
),
∵平行四边形ABCD的面积为
,
∴(3﹣m)?
=
,
解得m=
,
∴A(
,
),
∵平行四边形ABCD的一边AB∥y轴,顶点B在x轴上,
∴D(3,
),
∵点D在双曲线y2=
(k2>0,x>0)上,
∴k2=3×
=10.5,
故答案为:C.
10.【答案】
B
解:∵A,B分别在
和
的图象上,且A,B的纵坐标相同
∴设
∴
化简得:
故答案选:B
二、填空题
11.【答案】
1,2
解:本题考查的是反比例函数的图象的性质
由反比例函数的性质列出不等式,解出k的范围,在这个范围写出k的整数解则可.
由题意得k-3<0,k<3,则满足该条件的正整数k的值是1,2.
12.【答案】
x<0或x>3
解:
反比例函数??
,
当??时
,<2且x≠0,
若x>0,则2x>6,∴x>3,
若x<0,则2x<6,∴x<3,∴x<0,
综上所述:
x<0或x>3
13.【答案】
x<―2或0<x<3
解:把x=-2,y=-3和x=0,y=-1代入一次函数的解析式y1=k1x+b得,
,
解得,
,
∴一次函数的解析式为:y1=x-1;
把x=3,y=2代入反比例函数的解析式y2=
中得,
k=6,
∴反比例函数的解析式为:y2=
,
联立方程组
,
解得:
或
,
∴直线y1=x-1与双曲线y2=
的交点为:
(-2,-3)或(3,2),
作出草图如下:
由函数图象可知,当双曲线在直线上方时,x<-2或0<x<3,
∴关于x的不等式k1x+b<
的解集是:x<-2或0<x<3,
故答案为:x<-2或0<x<3.
14.【答案】
或
解:因为D
,勾股定理知,所以OD
=
=4,
所以A(
,7),所以反比例函数是y=
,
当D点移动到函数上时,纵坐标恰好和D相同,则3=
,x=
,所以移动了
个单位,
当B点移动到函数上时,B(0,4),4=
,x=
,所以移动了
个单位.
故答案为
或
.
15.【答案】
1<x<4
解:不等式
的解集实际上是反比例函数值小于一次函数值的自变量x的取值范围,根据图象得:1<x<4.
故答案为:1<x<4.
16.【答案】
12
解:如图,连接OC设AC交y轴于E.
∵AC⊥y轴于E,
∴S△AOE=2,S△OEC=4,
∴S△AOC=6,
∵A,B关于原点对称,
∴OA=OB,
∴S△ABC=2S△AOC=12,
故答案为:12.
17.【答案】
8
解:设:A、B、C三点的坐标分别是A(
,m)、B(
,m),
则:△ABC的面积=
?AB?yA=
?(
-
)?m=4,
则|k1-k2|=8.
故答案为8.
18.【答案】
-4
解:设A点坐标为(a,b),
∵△ABC和△BOD都是等腰直角三角形,
∴AB=
AC,OB=
BD,BC=AC,OD=BD
∵OB2-AB2=8,
∴2OD2-2AC2=8,即OD2-AC2=4,
∴(OD+AC)(OD-AC)=4,
又∵因为a<0,b>0,
∴a?b=-4
∴k=-4.
三、综合题
19.【答案】
(1)解:设反比例函数为:
∵反比例函数的图像经过点
∴
∴
∴反比例函数为:
;
(2)解:∵点
也在反比例函数图像上
∴
∴
∵
时,
∴
是
的解
∴
∴
、
两点间的距离
.
20.【答案】
(1)解:将点
代入反比例函数解析式中,得
解得:k=8
∴反比例函数解析式为
将点
代入反比例函数解析式中,得
解得:m=2
∴点
设直线OB的正比例函数解析式为y=ax
将点
代入,得
2=4a
解得:a=
∴直线OB的解析式为y=
x;
(2)解:∵
即
轴
∴点B的横坐标等于点C的横坐标8
将x=8代入y=
x中,解得y=4
∴点B的坐标为(8,4)
∴AB=4
∵点
∴AC=1
∴BC=AB-AC=3
21.【答案】
(1)解:把A(﹣1,a)代入y=x+6
得a=﹣1+6=5,
∴A(﹣1,5),
把B(b,1)代入y=x+6
得b+6=1,
解得:b=﹣5,
把A(﹣1,5)代入y
得k=﹣1×5=﹣5;
(2)解:∵A(﹣1,5),B(﹣5,1),
∴当一次函数的值大于反比例函数的值时,自变量x的取值范围为﹣5<x<﹣1;
(3)解:设直线y=x+6与x轴交于点C,连接OA,OB,如图,
则C(﹣6,0),
∴S△OAB=S△OAC﹣S△BOC
6×5
6×1
=12.
22.【答案】
(1)解:把点A(1,﹣4)的坐标代入y=
,得﹣4=
,求得k2=﹣4,
∴反比例函数y2=﹣
;
把点B(﹣2,m)的坐标代入y=﹣
,得m=﹣
=2
∴点B的坐标为(﹣2,2)
把点A(1,﹣4)、B(﹣2,2)分别代入y1=k1x+b,得
,
解得
,
∴一次函数y1=﹣2x﹣2;
(2)解:如图,
在一次函数y1=﹣2x﹣2中,令x=0,则y=﹣2,
∴直线AB与y轴的交点为E(0,﹣2),
∴S△AOB=S△AOE+S△BOE=
=3;
(3)解:由图象可知:y2>y1>0时,自变最x的取值范围是﹣2<x<0.
解:(3)∵点A(1,-4),点B(-2,2)
由题意可知:当﹣2<x<0时,
y2>y1>0
23.【答案】
(1)解:当x=n时,y=
,∴A(n,
),
由题意知BD是AC的中垂线,∴点B的纵坐标为
,
∴把y=
代入y=
得x=2n,∴B(2n,
)
(2)解:由(1)可知AM=CM,BM=MD=
,
∴四边形ABCD是平行四边形,
又∵BD⊥AC,∴平行四边形ABCD是菱形
(3)解:当四边形ABCD是正方形时,△ABM为等腰直角三角形,
∵△ABM的面积为2,∴AM=BM=2,∴A(-2,4),B(-4,2),
由此可得直线AB所对应的函数表达式为y=x+6.
24.【答案】
(1)解:把C点坐标代入反比例函数中得
?
解得m=4
在把C(1,4)代入一次函数中得
?
解得n=2
(2)解:由(1)知一次函数和反比例函数的解析式为
和
则A点坐标为(-1,0)
AD=4
把x=3分别代入得
y=8和y=
则P点坐标为(3,5),Q点坐标为(3,
)
则PQ=
△APQ的面积=
=
=
(3)解:
<0可以看成
函数y=kx+b的图像在
图像的下方时x的取值范围
由图像得Q点的右边和C点的左边时,
y=kx+b的图像在
的下方,
即x<1或者x>3.
(4)x=1或x=3
解:(4)由图像知在C点和Q点时
y=kx+b和
相交,
所以
=0的解为x=1或x=3.
25.【答案】
(1)解:∵
面积为3,
,
∴
,即
,
∴
,
∵反比例函数为
过点
,
∴
,即反比例函数为:
,
∵反比例函数为
,
(2)解:∵点
在反比例函数
上,
∴
∴
.
.
∵直线
经过点
∴
解得:
线
的解析式为:
.
(3)解:连OC,
∴M点的坐标为(2,0),
∴S△AOC=S△AOM+S△COM=
×2×3+
×2×
=
;
(4)解:如图,
∵点A(-2,3),点O(0,0)
当x≤-2时,
,
当-2≤x<0时,;
∵点B(4,),点O(0,0)
∴当0<x≤4时
,
当x>4时,;
∴不等式
的解集是x≤?2或0<x≤4.
26.【答案】
(1)解:y=
x(0≤x≤10)
y=
?(x≥10)
(2)解:把y=1.6代入y=
x可得x=2
把y=1.6
代入y=
可得x=50
根据图象,当y≥1.6时,2≤x≤50
即从消毒开始后的第2分至50分内消毒人员不可以留在教室里.
(3)解:把y=3.2代入y=
x可得x=4
把y=3.2代入y=
可得x=25
∵25-4>20
∴本次消毒有效
27.【答案】
(1)解:如图1,当点A在x轴正半轴,点B在y轴负半轴上时,
∵OC=OD=1,
∴正方形ABCD的边长CD=
;
∵当点A在x轴负半轴、点B在y轴正半轴上时,
∴设正方形的边长为a,
∴3a=CD=
.
∴a=
,
∴正方形边长为
,
∴一次函数y=x+1图象的伴侣正方形的边长为
或
;
(2)解:如图2,作DE,CF分别垂直于x、y轴,
∵AB=AD=BC,∠DAE=∠OBA=∠FCB,
∴△ADE≌△BAO≌△CBF.
∵m<2,
∴DE=OA=BF=m,OB=CF=AE=2﹣m,
∴OF=BF+OB=2,
∴C点坐标为(2﹣m,2),
设反比例函数的解析式为:
,
∵D(2,m),C(2﹣m,2)
∴
,
∴由②得:k=2m③,
∴把k=2m代入①得:2m=2(2﹣m),
∴解得m=1,k=2,
∴反比例函数的解析式为y=
.
28.【答案】
(1)t=1时,E点坐标为(1,2),F点横坐标x=2,
设经过E的双曲线为?
,
把E点坐标代入得:
,
再把F点横坐标x=2代入
,
得y=1,所以F点坐标为(2,1).
(2)因为A点坐标为(1,0),G点坐标为(1,1),
则t秒后,E点坐标可以表示为(1,1+t),
B点坐标可以表示为(1+t,0),
设经过E点双曲线为:
,
把E点坐标代入得:
,
F点也在双曲线上,F点横坐标和B相同,
把x=1+t代入函数
得,
y=1,所以F点坐标为(1+t,1),
因为AE
BC,所以
,
又EB平分
,所以
,
EF=BF,
即
,
解得t=
.
(3)因为D点坐标为(1,3),M为DC中点,则M点坐标为(1,
),
又
是直角,所以
是直角三角形,
由勾股定理
,
得:
,
解得t=
.
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
