相似三角形复习

(共21张PPT)
1.相似三角形的定义：
对应角相等、对应边成比例的三角形叫做相似三角形。
2.相似比：
相似三角形的对应边的比，叫做相似三角形的相似比。
△ABC∽△A/B/C/,如果BC=3,B/C/=1.5,那么△A/B/C/与 △ABC的相似比为( ).
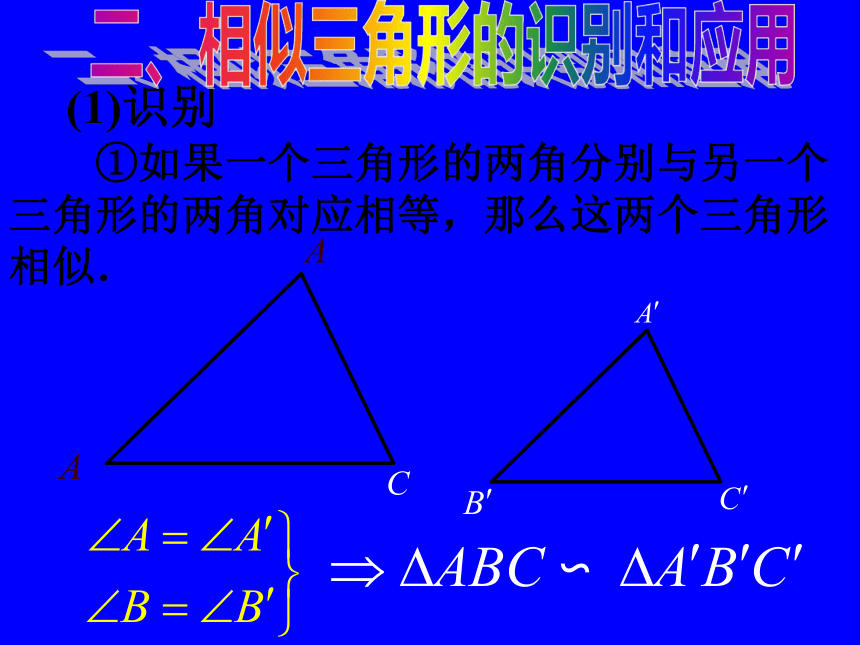
(1)识别
　　①如果一个三角形的两角分别与另一个三角形的两角对应相等，那么这两个三角形相似．
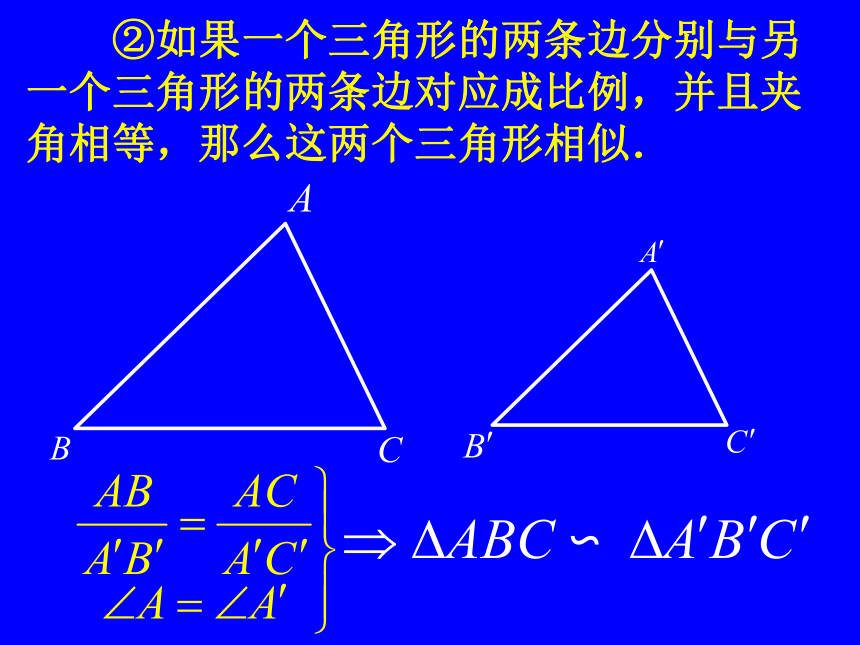
　　②如果一个三角形的两条边分别与另一个三角形的两条边对应成比例，并且夹角相等，那么这两个三角形相似．
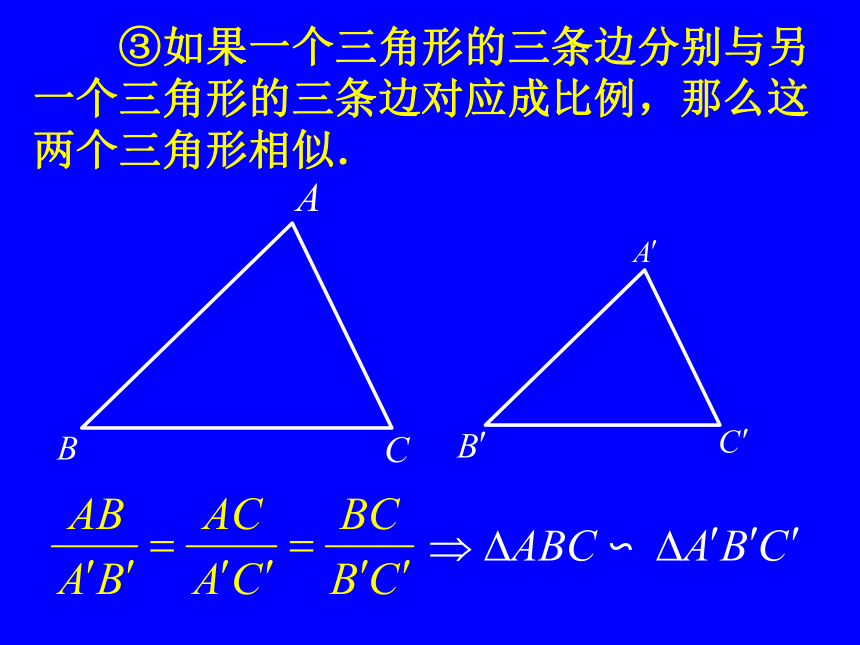
　　③如果一个三角形的三条边分别与另一个三角形的三条边对应成比例，那么这两个三角形相似．
(2)性质
两个三角形相似，则
③它们的周长比等于相似比；面积比等于相似比的平方．
①它们的对应边成比例，对应角相等；
②它们的对应高、对应中线、对应角平分线的比等于相似比；
应用举例
例1 判断
①所有的等腰三角形都相似．
②所有的直角三角形都相似．
③所有的等边三角形都相似．
④所有的等腰直角三角形都相似．
(×)
(√)
(√)
(×)
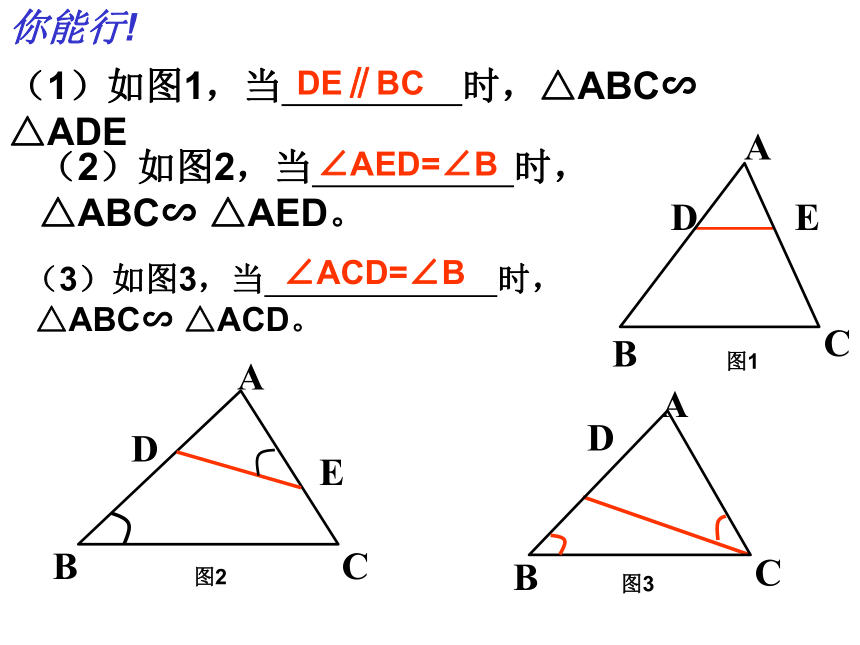
你能行!
（1）如图1，当 时，△ABC∽ △ADE
A
B
C
D
E
图1
（2）如图2，当 时，
△ABC∽ △AED。
A
B
C
D
E
图2
（3）如图3，当 时，
△ABC∽ △ACD。
A
B
C
D
图3
DE∥BC
∠AED=∠B
∠ACD=∠B
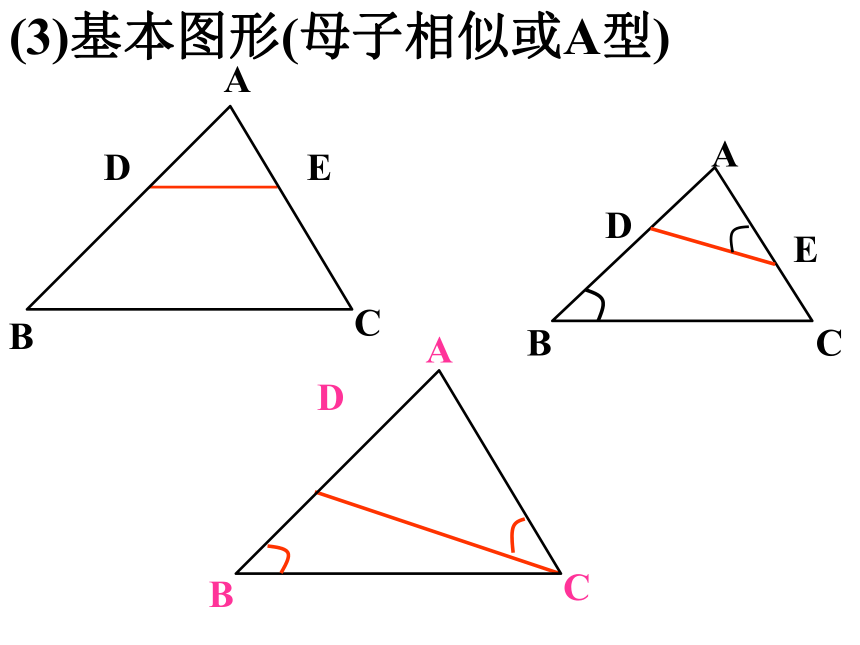
(3)基本图形(母子相似或A型)
A
B
C
D
E
A
B
C
D
A
B
C
D
E
（1）如图1当AB∥ED时，则△ ∽△ 。
（2）如图2，当 时，则△ ∽△ 。
A
B
C
D
E
图1
A’
B’
C’
D’
E’
图2
ABC DEC
∠B’= ∠E’或
A’B’C’ D’E’C’
你能行!
（兄弟相似或X型）
A
B
C
D
E
A’
B’
C’
D’
E’
(4)特殊图形
A
B
C
D
∵∠BAC=90°
（双垂直型）
∴
△ ∽ △ ∽ △
ABC DBA DAC
例1、 如图1,已知:DE∥BC,
EF ∥AB,则图中共
有_____对三角形相似.
3
A
B
C
D
E
F
如图(1)
例2:已知,如图,梯形ABCD中,AD∥BC, ∠A=900,对角线BD⊥CD
求证:(1) △ABD∽△DCB;
(2)BD2=AD·BC
A
B
C
D
例3. 正方形ABCD的边长为8，E是AB的中点，点M，N分别在BC，CD上，且CM=2，则当CN=_______时，△CMN与△ADE形状相同。
1
或4
如图,在△ABC和△DEF中, ∠A=∠D=70°, ∠B=50°, ∠E=30°,过顶点画直线a,把△ABC分成两个三角形,过顶点画直线b ,把△DEF分成两个三角形,使△ABC分成的两个三角形和△DEF分成的两个三角形分别相似.(要求标注数据)
C
A
B
700
500
E
D
F
700
300
300
C
A
B
700
500
a
300
E
D
F
700
300
b
E
D
F
700
300
b
200
C
A
B
700
500
a
200
在平面直角坐标系，B（1，0）, A（3，－3）, C（3，0）,点P在y轴的正半轴上运动，若以O，B，P为顶点的三角形与△ABC相似，则点P的坐标是__________________.
y
·A
B
C
x
·
·
O
在方格纸中，每个小格的顶点称为格点，以格点的连线为边的三角形称为格点三角形，如图所示的5×5的方格纸中，如果想作格点ΔABC与ΔOAB相似(相似比不能为1)，则C点坐标为____________．
O
x
A
B
y
O
x
A
B
y
1
2
C1(5，2)
5
C2(4，4)
例2 如图，CD是Rt△ABC斜边上的高，
E为AC的中点，ED交CB的延长线于F。
C
E
A
D
F
B
求证：BD·CF=CD·DF