列方程组解应用题（配套问题）课件

(共15张PPT)
分析：
1、哪几个量已知？哪几个量未知？
2、怎样设未知数？
4、等量关系：
（1）______________+_________________=28（人）
（2）____________=_________________
3、列表
x
y
12x
18y
生产螺栓人数
生产螺帽人数
螺帽个数
螺栓个数的2倍
例1
、某车间有28名工人，生产一种螺栓和螺帽，平均每人每时能生产螺栓12个或螺帽18个，应分配多少人生产螺栓,多少人生产螺帽，才能使生产出的螺栓和螺帽刚好配套（每一个螺栓要配两个螺帽）？
例1
、某车间有28名工人，生产一种螺栓和螺帽，平均每人每时能生产螺栓12个或螺帽18个，应分配多人生产螺栓,多少人生产螺帽，才能使生产出的螺栓和螺帽刚好配套（每一个螺栓要配两个螺帽）？
解：设分配x人生产螺栓，y人生产螺帽.由题意，得：
答：应分配12人生产螺栓，16人生产螺帽.
配套问题
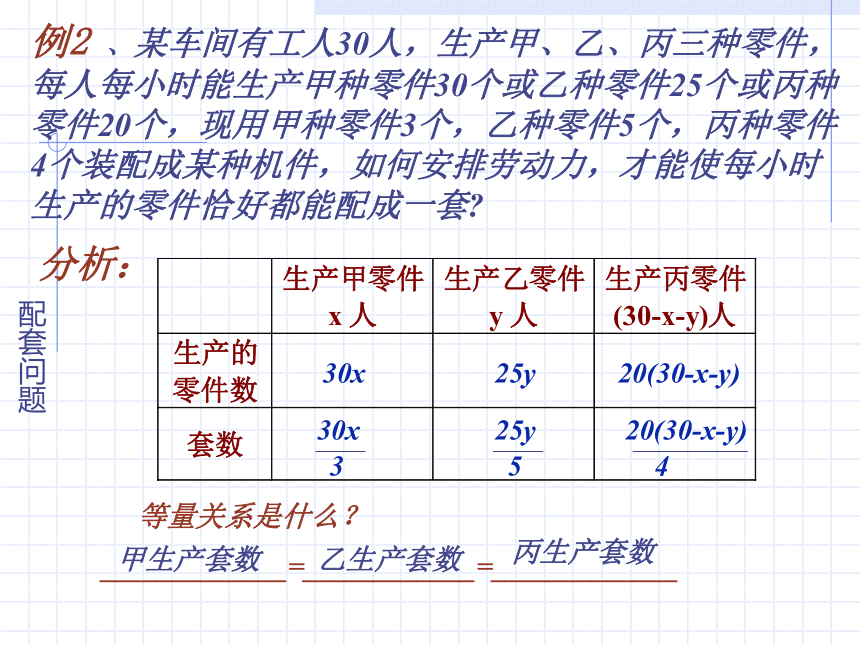
例2
、某车间有工人30人，生产甲、乙、丙三种零件，每人每小时能生产甲种零件30个或乙种零件25个或丙种零件20个，现用甲种零件3个，乙种零件5个，丙种零件4个装配成某种机件，如何安排劳动力，才能使每小时生产的零件恰好都能配成一套?
分析：
等量关系是什么？
_____________=____________=_____________
30x
25y
20(30-x-y)
30x
3
25y
5
20(30-x-y)
4
甲生产套数
乙生产套数
丙生产套数
配套问题
例2
、某车间有工人30人，生产甲、乙、丙三种零件，每人每小时能生产甲种零件30个或乙种零件25个或丙种零件20个，现用甲种零件3个，乙种零件5个，丙种零件4个装配成某种机件，如何安排劳动力，才能使每小时生产的零件恰好都能配成一套?
解：设生产甲零件x人，生产乙零件y人，则生产丙零件为(30-x-y)人；由题意得：
答：分配6人生产零件甲，分配12人生产零件乙，分配12人生产零件丙.
配套问题
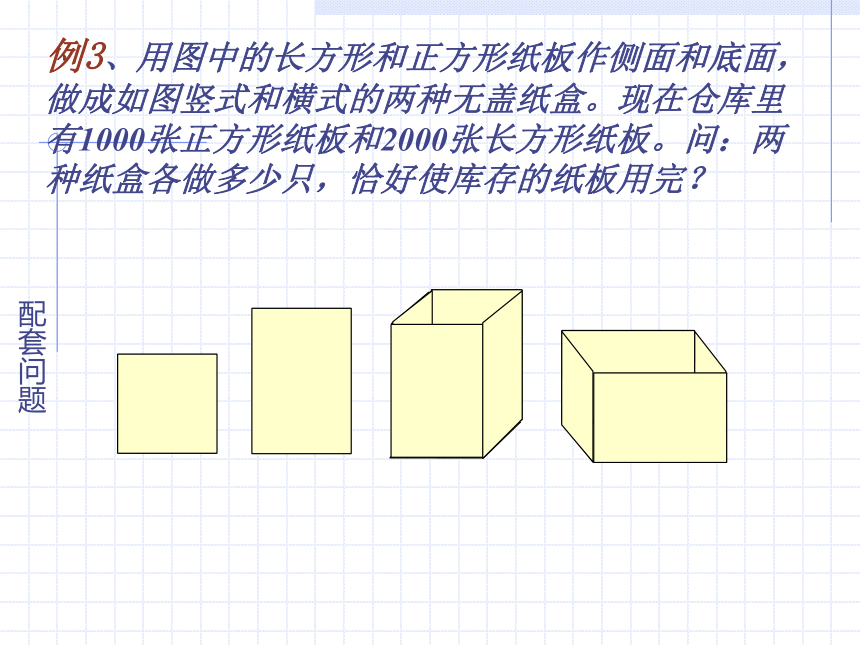
例3、用图中的长方形和正方形纸板作侧面和底面，做成如图竖式和横式的两种无盖纸盒。现在仓库里有1000张正方形纸板和2000张长方形纸板。问：两种纸盒各做多少只，恰好使库存的纸板用完？
配套问题
例3、用图中的长方形和正方形纸板作侧面和底面，做成如图竖式和横式的两种无盖纸盒。现在仓库里有1000张正方形纸板和2000张长方形纸板。问：两种纸盒各做多少只，恰好使库存的纸板用完？
配套问题
例3、用图中的长方形和正方形纸板作侧面和底面，做成如图竖式和横式的两种无盖纸盒。现在仓库里有1000张正方形纸板和2000张长方形纸板。问：两种纸盒各做多少只，恰好使库存的纸板用完？
一个横式纸盒要用____张长方形和_____张正方形.
一个竖式纸盒要用____张长方形和_____张正方形.
4
1
3
2
配套问题
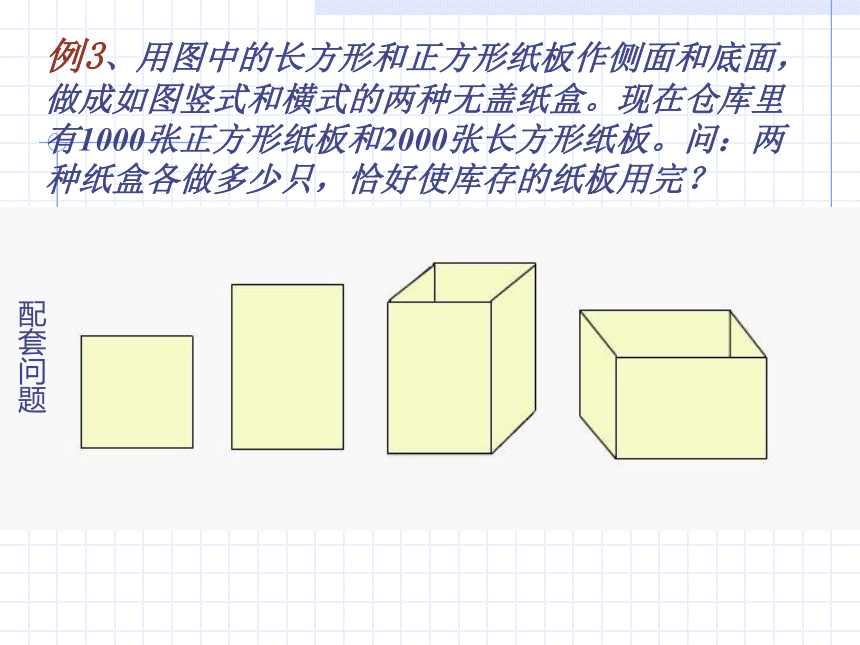
例3、用图中的长方形和正方形纸板作侧面和底面，做成如图竖式和横式的两种无盖纸盒。现在仓库里有1000张正方形纸板和2000张长方形纸板。问：两种纸盒各做多少只，恰好使库存的纸板用完？
一个横式纸盒要用____张长方形和_____张正方形.
一个竖式纸盒要用____张长方形和_____张正方形.
4
1
3
2
分析：
x
4x
2y
3y
配套问题
1000
2000
例3、用图中的长方形和正方形纸板作侧面和底面，做成如图竖式和横式的两种无盖纸盒。现在仓库里有1000张正方形纸板和2000张长方形纸板。问：两种纸盒各做多少只，恰好使库存的纸板用完？
解：设做竖式纸盒x个，横式纸盒y个，由题意：
答：竖式纸盒做200个，横式纸盒做400个.
配套问题
如果把仓库里的纸板数改成已知库存的正方形纸板与长方形纸板的张数之比为1：3，糊成两种纸盒后，库存纸板恰好用完，求竖式纸盒与横式纸盒的个数之比。
配套问题
Ａ
a
3a
变式
如果把仓库里的纸板数改成已知库存的正方形纸板与长方形纸板的张数之比为1：3，糊成两种纸盒后，库存纸板恰好用完，求竖式纸盒与横式纸盒的个数之比。
解：设做竖式纸盒x个，横式纸盒y个，
正方形纸板为a张，长方形的纸板3a张，由题意得：
答：竖式纸盒与横式纸盒之比为3：1
所以，x:y=3:1
配套问题
练习
1、某工地派96人去挖土和运土，如果平均每人每天挖土5立方米或运土3立方米，那么怎样分配挖土和运土的人数，使挖出的土刚好能及时运走？
2、某服装厂加工一种工作服，裁剪组每人每天可裁工作服15件，缝纫组每人每天可做工作服5件，现有技术工人16人，接受一批定货任务，问最好应分配几个人裁，几个做？
配套问题
3、如果例3中，如果正方形纸板500张，长方形纸板1001张，那么，能否做成若干只两种纸盒后，恰好把库存纸板用完？
小结：
本节学习了用方程组解应用题中的配套问题
配套问题
1：学会用“列表法”分析题意，从而找出等量关系。
2：为了解决问题方便，常运用引进“辅助元”的思想方法。
3：数学来于源实践，并应用于实践生活。