5.3 变化的鱼 课件

(共14张PPT)
5.3 变 化 的 鱼
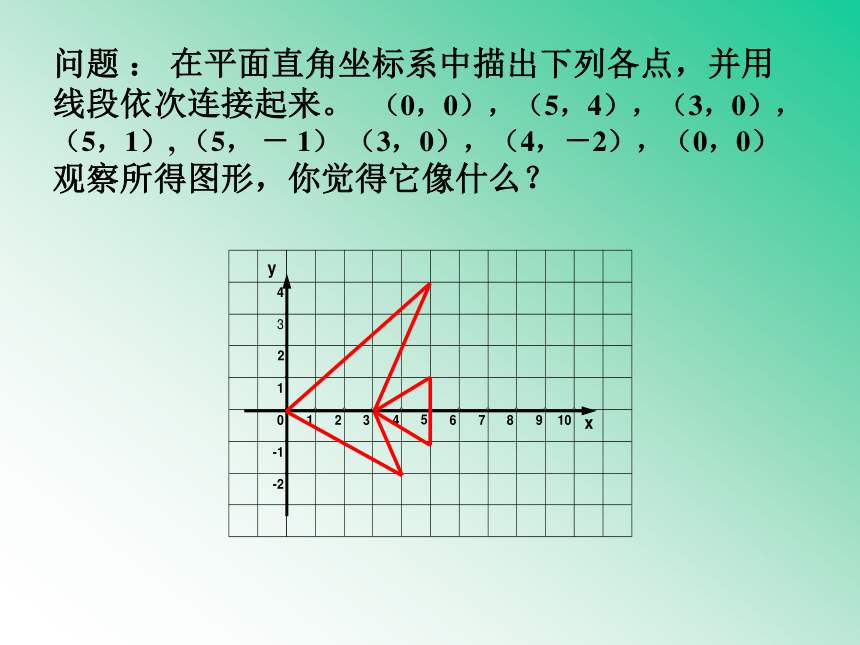
问题 ： 在平面直角坐标系中描出下列各点，并用线段依次连接起来。 （0，0），（5，4），（3，0），（5，1）, （5， － 1） （3，0），（4，－2），（0，0）观察所得图形，你觉得它像什么？
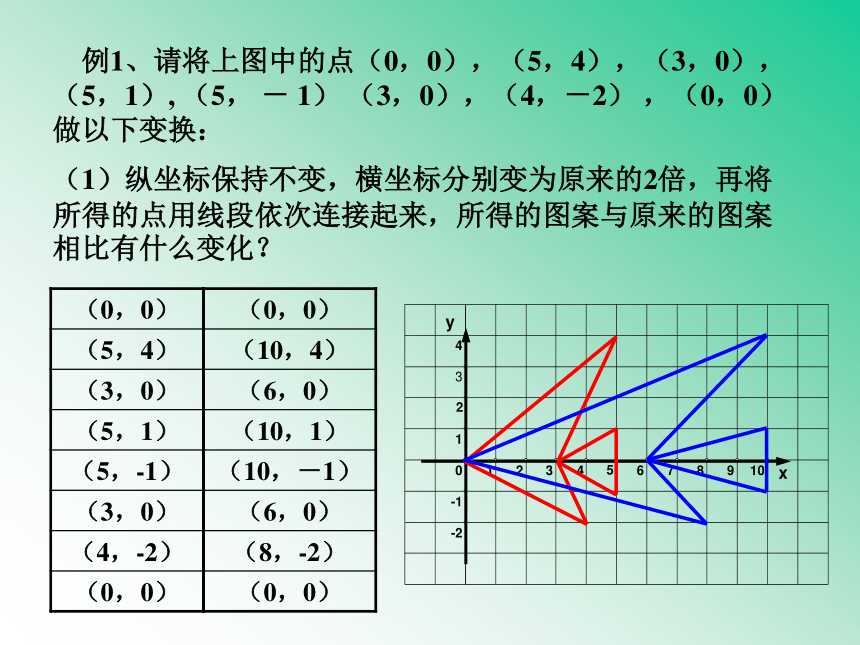
例1、请将上图中的点（0，0），（5，4），（3，0），（5，1）, （5， － 1） （3，0），（4，－2） ，（0，0）做以下变换：
（1）纵坐标保持不变，横坐标分别变为原来的2倍，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？
（0，0）
（5，4）
（3，0）
（5，1）
（5，-1）
（3，0）
（4，-2）
（0，0）
（0，0）
（10，4）
（6，0）
（10，1）
（10，－1）
（6，0）
（8，-2）
（0，0）
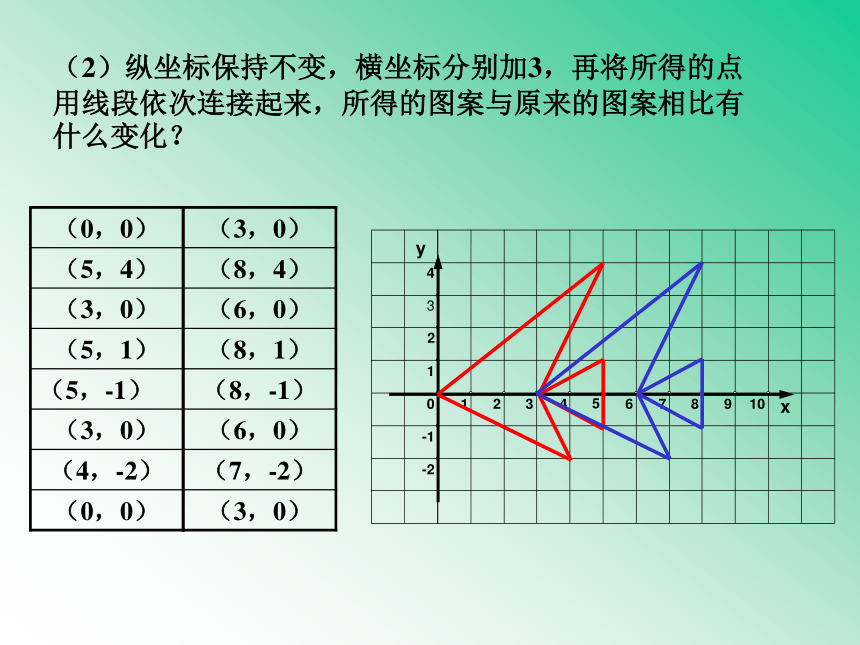
（2）纵坐标保持不变，横坐标分别加3，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？
（0，0）
（5，4）
（3，0）
（5，1）
（5，-1）
（3，0）
（4，-2）
（0，0）
（3，0）
（8，4）
（6，0）
（8，1）
（8，-1）
（6，0）
（7，-2）
（3，0）
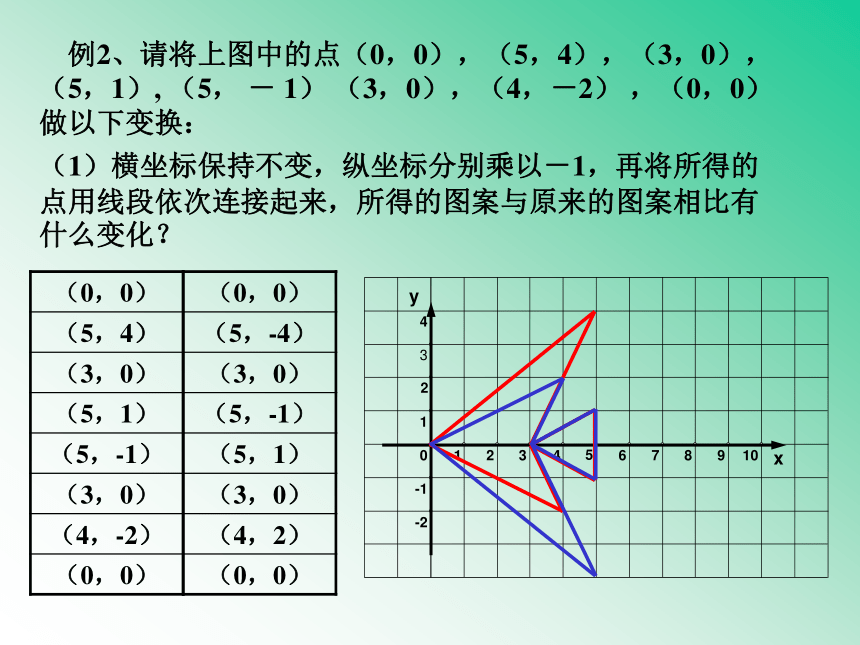
例2、请将上图中的点（0，0），（5，4），（3，0），（5，1）, （5， － 1） （3，0），（4，－2） ，（0，0）做以下变换：
（1）横坐标保持不变，纵坐标分别乘以－1，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？
（0，0）
（5，4）
（3，0）
（5，1）
（5，-1）
（3，0）
（4，-2）
（0，0）
（0，0）
（5，-4）
（3，0）
（5，-1）
（5，1）
（3，0）
（4，2）
（0，0）
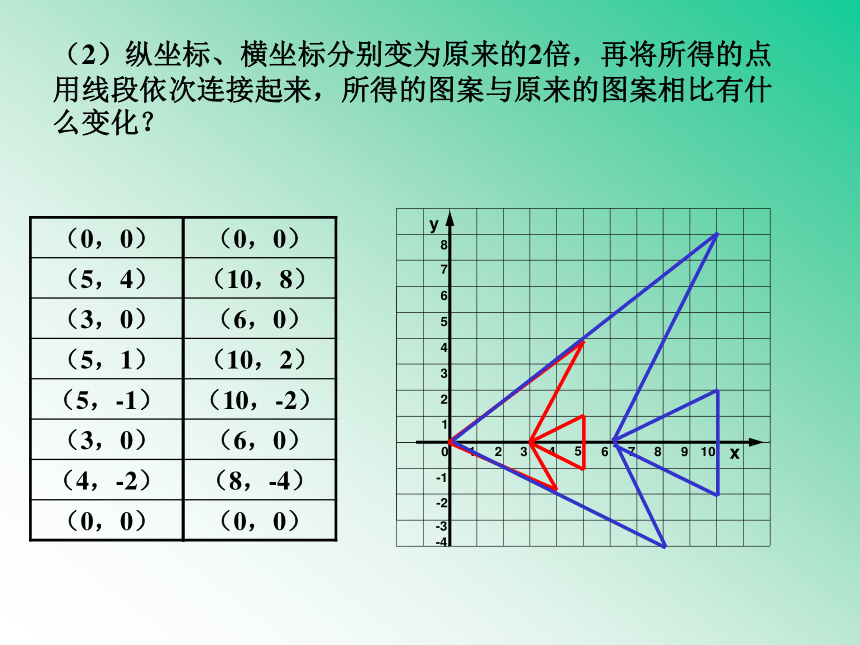
（2）纵坐标、横坐标分别变为原来的2倍，再将所得的点用线段依次连接起来，所得的图案与原来的图案相比有什么变化？
（0，0）
（5，4）
（3，0）
（5，1）
（5，-1）
（3，0）
（4，-2）
（0，0）
（0，0）
（10，8）
（6，0）
（10，2）
（10，-2）
（6，0）
（8，-4）
（0，0）
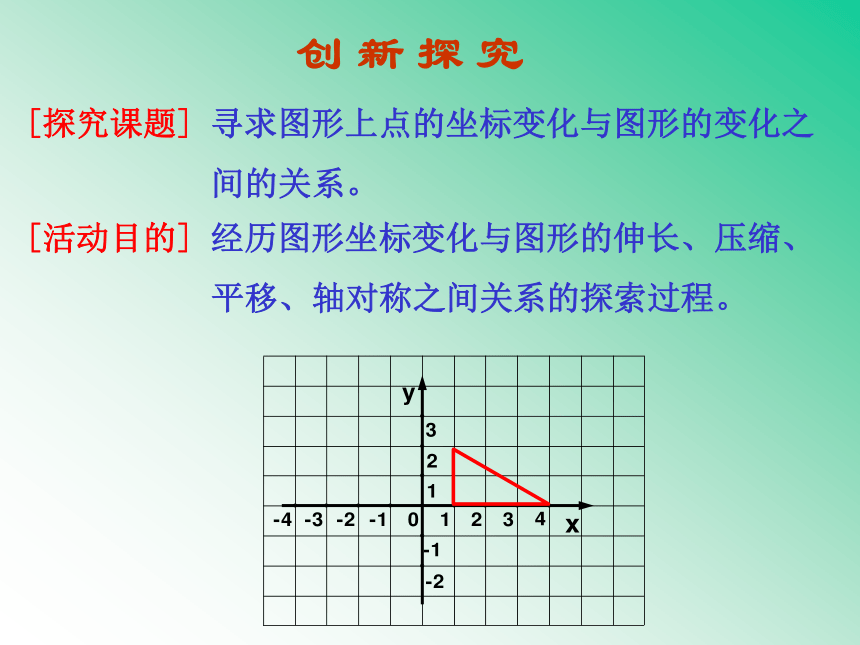
创 新 探 究
[探究课题] 寻求图形上点的坐标变化与图形的变化之
间的关系。
[活动目的] 经历图形坐标变化与图形的伸长、压缩、
平移、轴对称之间关系的探索过程。
（1）
（2）
（3）
（4）
（5）
（6）
1.纵坐标不变，横坐标分别增加（减少）a个单位时，图形向右（向左）平移 a个 单位；
2.横坐标不变，纵坐标分别增加（减少） a个单位时，图形向上（向下）平移a个单位；
课堂小结：
3.纵坐标不变，横坐标分别变为原来的a倍，图形横向伸长为原来的a倍（a>1）
或图形横向缩短为原来的a倍（04.横坐标与纵坐标同时变为原来的a倍，图形变为原来的a倍；
（a>1）
（05.纵坐标不变，横坐标分别乘-1，所得图形与原图形关于Y轴对称；
6.横坐标不变，纵坐标分别乘-1，所得图形与原图形关于X轴对称；
7.横坐标与纵坐标都乘-1，所得图形与原图形关于原点成中心对称；
感谢各位老师莅临指导