5.1 导数的定义及几何意义 同步练习 (含解析)
文档属性
| 名称 | 5.1 导数的定义及几何意义 同步练习 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 96.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-24 00:00:00 | ||
图片预览



文档简介
(
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
人教A版2019
选修二
5.1
导数的定义及几何意义同步练习
一、单选题
1.函数f(x)在x=x0处的导数可表示为(??
)
A.?f′(x0)=
???????????????????????????B.?f′(x0)=
C.?f′(x0)=f(x0+Δx)-f(x0)?????????????????????????????????????D.?f′(x0)=
2.函数
的图像在点
处的切线方程是
,则
(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
3.已知曲线
在点
处切线的斜率为1,则实数
的值为(
??)
A.?2?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?-1
4.已知曲线
的一条切线的斜率为
,则切点的横坐标为(??
)
A.????????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
5.函数
的图象在点
处的切线的倾斜角为(??
)
A.?0??????????????????????????????????????????B.???????????????????????????????????????????C.?1??????????????????????????????????????????D.?
6.设曲线
在
处的切线斜率为
,则
的值为(???
)
A.?????????????????????????????B.?-1????????????????????????????C.?????????????????????????????D.?1
7.汽车行驶的路程s和时间t之间的函数图象如图,在时间段
上的平均速度分别为
,则三者的大小关系为(???
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
8.曲线
在
处的切线
过原点,则
的方程是(???
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
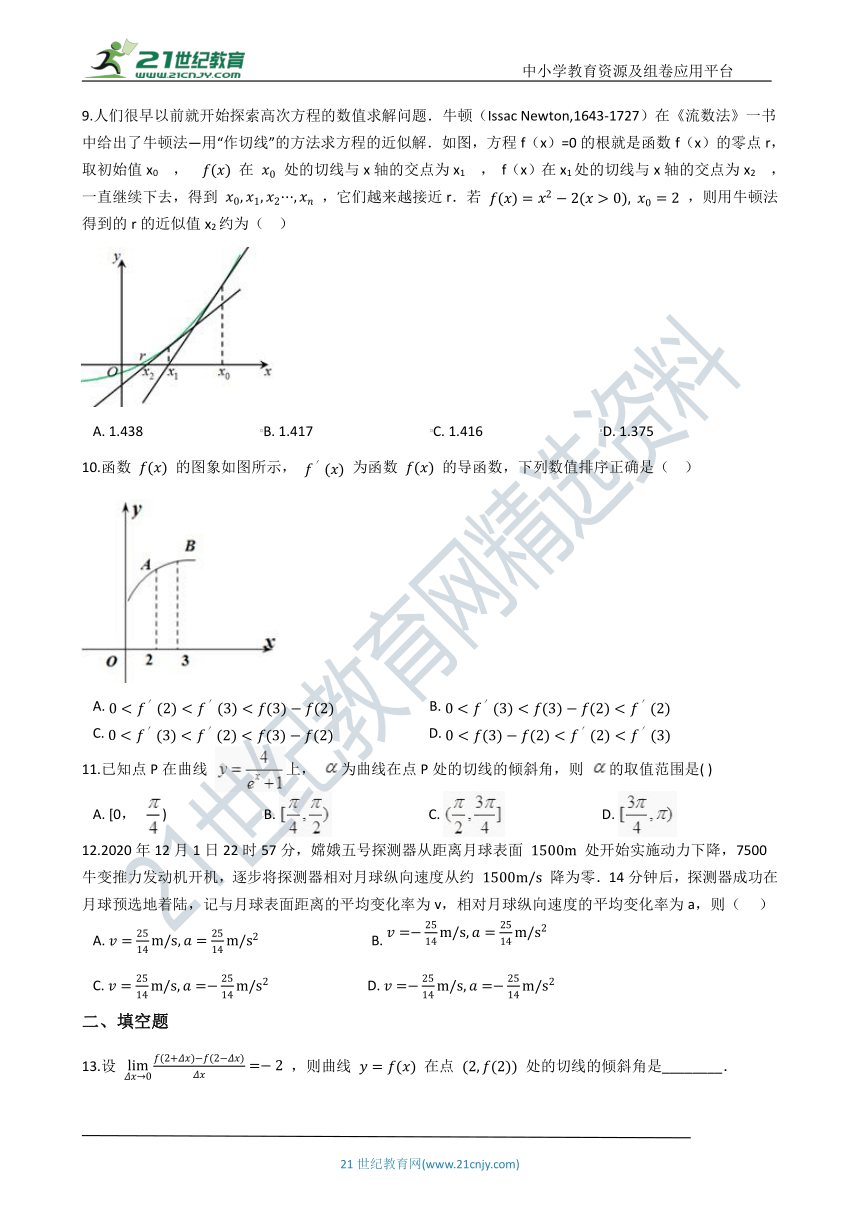
9.人们很早以前就开始探索高次方程的数值求解问题.牛顿(Issac
Newton,1643-1727)在《流数法》一书中给出了牛顿法—用“作切线”的方法求方程的近似解.如图,方程f(x)=0的根就是函数f(x)的零点r,取初始值x0
,
在
处的切线与x轴的交点为x1
,
f(x)在x1处的切线与x轴的交点为x2
,
一直继续下去,得到
,它们越来越接近r.若
,则用牛顿法得到的r的近似值x2约为(??
)
A.?1.438??????????????????????????????????B.?1.417??????????????????????????????????C.?1.416??????????????????????????????????D.?1.375
10.函数
的图象如图所示,
为函数
的导函数,下列数值排序正确是(??
)
A.????????????????????????????B.?
C.????????????????????????????D.?
11.已知点P在曲线
上,
为曲线在点P处的切线的倾斜角,则
的取值范围是(
)
A.?[0,
)????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
12.2020年12月1日22时57分,嫦娥五号探测器从距离月球表面
处开始实施动力下降,7500牛变推力发动机开机,逐步将探测器相对月球纵向速度从约
降为零.14分钟后,探测器成功在月球预选地着陆,记与月球表面距离的平均变化率为v,相对月球纵向速度的平均变化率为a,则(???
)
A.?????????????????????????????????B.?
C.?????????????????????????????D.?
二、填空题
13.设
,则曲线
在点
处的切线的倾斜角是________.
14.对于三次函数
,定义:设
是函数
的导数
的导数,若方程
有实数解
,则称点
为函数
的“拐点”,有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”根据此发现,若函数
,计算
________.
15.若直线
是曲线
的切线,也是曲线
的切线,则
________.
16.已知函数
的图像在点
处的切线方程是
,则
________.
三、解答题
17.设
是二次函数,其图象过点
,且在点
处的切线为
.
(1)求
的表达式;
(2)求
的图象与两坐标轴所围成图形的面积.
18.已知曲线
y
=
x3
+
x-2
在点
P0
处的切线
平行于直线4x-y-1=0,且点
P0
在第三象限,
(1)求P0的坐标;
(2)若直线
,
且
l
也过切点P0
,求直线l的方程.
19.已知曲线
在点
处的切线方程是
.
(1)求
,
的值;
(2)如果曲线
的某一切线与直线
:
垂直,求切点坐标与切线的方程.
20.已知函数f(x)=
x3-2x2+3x(x∈R)的图象为曲线C.
(1)求过曲线C上任意一点切线斜率的取值范围;
(2)若在曲线C上存在两条相互垂直的切线,求其中一条切线与曲线C的切点的横坐标的取值范围.
答案解析部分
一、单选题
1.【答案】
A
解:B中f′(x0)=
,右边的式子表示函数值的变化量的极限,趋近于0;C中f′(x0)=f(x0+Δx)-f(x0),右边的式子表示函数值的变化量;D中f′(x0)=
,右边的式子表示函数的平均变化率.
故答案为:A
2.【答案】
B
解:当x=5时,y=3,即f(5)=3,又
,
则
,
故答案为:B.
3.【答案】
D
解:因为
,?
,?
因为
处切线斜率为1,所以
,?
,解得
,
故答案为:D.
4.【答案】
D
解:
,设切点横坐标为
,
。
故答案为:D
5.【答案】
B
解:欲判别切线的倾斜角的大小,只须求出其斜率的正负即可,故先利用导数求出在x=4处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决,根据题意,由于
,则可知
,那么可知f’(0)=1,可知该点的切线的斜率为1,可知倾斜角为
。
故答案为:B.
6.【答案】
B
解:由题得
所以
,
。
故答案为:B
7.【答案】
C
解:由题意得,
,由题图易知
,
∴
,
故答案为:C.
8.【答案】
A
解:解:曲线
,
,切点为
,
所以切线
的斜率
,
又直线
过原点,所以
,
得
,
.所以
,故切线
的方程为
即
.
故答案为:A.
9.【答案】
B
解:解:f(x)=x2-2(x>0),则f'(x)=2x(x>0),当x0=2时,f(x0)=2,f'(x0)=4,则切线方程为y-2=4(x-2),
令y=0,则x1=1.5,f(x1)=0.25,f'(x1)=3,则切线方程为y-0.25=3(x-1.5),再令y=0,则x2≈1.417,所以B正确.
故答案为:B
10.【答案】
B
解:由
图象可知,
在
处的切线斜率大于在
处的切线斜率,且斜率为正,
,
,
可看作过
和
的割线的斜率,由图象可知
,
.
故选:
.
11.【答案】
D
解:因为,
,所以,
,即
,由
,所以,
的取值范围是
,故选D。
12.【答案】
D
解:解:探测器与月球表面距离逐渐减小,所以
;
探测器的速度逐渐减小,所以
。
故答案为:D。
二、填空题
13.【答案】
解:因为
=
,
所以
,
则曲线
在点
处的切线斜率为
,即
,
又
所以所求切线的倾斜角
为
.
故答案为:
14.【答案】
2019
解:由题可知:
,则
,
所以
令
,则
,又
,
故
的对称中心为
,故
,
令
所以
所以
,则
故答案为:2019.
15.【答案】
1-ln2
解:对函数
求导得
,对
求导得
,设直线
与曲线
相切于点
,与曲线
相切于点
,则
,由点
在切线上得
,由点
在切线上得
,这两条直线表示同一条直线,所以
,解得
。
16.【答案】
1
解:因为函数
的图像在点
处的切线方程是
,
即
,且
故
故答案为:1
三、解答题
17.【答案】
(1)解:设
,
过点
,
,
在点
处的切线为
且
,
,解得:
,
;
(2)解:
的图象与两坐标轴所围成的图形如下图阴影部分所示,
所求面积
.
18.【答案】
(1)解:由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.
当x=1时,y=0;
当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为(-1,-4);
(2)解:∵直线
l⊥l1
,
l1的斜率为4,
∴直线l的斜率为-1/
4
,
∵l过切点P0
,
点P0的坐标为(-1,-4)
∴直线l的方程为y+4=
(x+1)即x+4y+17=0.
19.【答案】
(1)解:∵
的导数
,
由题意可得
,
,
解得
,
.
(2)解:∵切线与直线
垂直,
∴切线的斜率
.设切点的坐标为
,
则
,∴
.
由
,可得
,或
.
则切线方程为
或
.
即
或
.
20.【答案】
(1)解:由题意得f′(x)=x2-4x+3,则f′(x)=(x-2)2-1≥-1,
即过曲线C上任意一点切线斜率的取值范围是[-1,+∞).
(2)解:设曲线C的其中一条切线的斜率为k,则由(2)中条件并结合(1)中结论可知,
解得-1≤k<0或k≥1,故由-1≤x2-4x+3<0或x2-4x+3≥1,
得x∈(-∞,2-
]∪(1,3)∪[2+
,+∞)
21世纪教育网(www.21cnjy.com)
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
)
中小学教育资源及组卷应用平台
人教A版2019
选修二
5.1
导数的定义及几何意义同步练习
一、单选题
1.函数f(x)在x=x0处的导数可表示为(??
)
A.?f′(x0)=
???????????????????????????B.?f′(x0)=
C.?f′(x0)=f(x0+Δx)-f(x0)?????????????????????????????????????D.?f′(x0)=
2.函数
的图像在点
处的切线方程是
,则
(??
)
A.?1???????????????????????????????????????????B.?2???????????????????????????????????????????C.?3???????????????????????????????????????????D.?4
3.已知曲线
在点
处切线的斜率为1,则实数
的值为(
??)
A.?2?????????????????????????????????????????B.??????????????????????????????????????????C.??????????????????????????????????????????D.?-1
4.已知曲线
的一条切线的斜率为
,则切点的横坐标为(??
)
A.????????????????????????????????????????????B.?1???????????????????????????????????????????C.?2???????????????????????????????????????????D.?3
5.函数
的图象在点
处的切线的倾斜角为(??
)
A.?0??????????????????????????????????????????B.???????????????????????????????????????????C.?1??????????????????????????????????????????D.?
6.设曲线
在
处的切线斜率为
,则
的值为(???
)
A.?????????????????????????????B.?-1????????????????????????????C.?????????????????????????????D.?1
7.汽车行驶的路程s和时间t之间的函数图象如图,在时间段
上的平均速度分别为
,则三者的大小关系为(???
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
8.曲线
在
处的切线
过原点,则
的方程是(???
)
A.???????????????????????B.???????????????????????C.???????????????????????D.?
9.人们很早以前就开始探索高次方程的数值求解问题.牛顿(Issac
Newton,1643-1727)在《流数法》一书中给出了牛顿法—用“作切线”的方法求方程的近似解.如图,方程f(x)=0的根就是函数f(x)的零点r,取初始值x0
,
在
处的切线与x轴的交点为x1
,
f(x)在x1处的切线与x轴的交点为x2
,
一直继续下去,得到
,它们越来越接近r.若
,则用牛顿法得到的r的近似值x2约为(??
)
A.?1.438??????????????????????????????????B.?1.417??????????????????????????????????C.?1.416??????????????????????????????????D.?1.375
10.函数
的图象如图所示,
为函数
的导函数,下列数值排序正确是(??
)
A.????????????????????????????B.?
C.????????????????????????????D.?
11.已知点P在曲线
上,
为曲线在点P处的切线的倾斜角,则
的取值范围是(
)
A.?[0,
)????????????????????????????B.?????????????????????????????C.?????????????????????????????D.?
12.2020年12月1日22时57分,嫦娥五号探测器从距离月球表面
处开始实施动力下降,7500牛变推力发动机开机,逐步将探测器相对月球纵向速度从约
降为零.14分钟后,探测器成功在月球预选地着陆,记与月球表面距离的平均变化率为v,相对月球纵向速度的平均变化率为a,则(???
)
A.?????????????????????????????????B.?
C.?????????????????????????????D.?
二、填空题
13.设
,则曲线
在点
处的切线的倾斜角是________.
14.对于三次函数
,定义:设
是函数
的导数
的导数,若方程
有实数解
,则称点
为函数
的“拐点”,有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”根据此发现,若函数
,计算
________.
15.若直线
是曲线
的切线,也是曲线
的切线,则
________.
16.已知函数
的图像在点
处的切线方程是
,则
________.
三、解答题
17.设
是二次函数,其图象过点
,且在点
处的切线为
.
(1)求
的表达式;
(2)求
的图象与两坐标轴所围成图形的面积.
18.已知曲线
y
=
x3
+
x-2
在点
P0
处的切线
平行于直线4x-y-1=0,且点
P0
在第三象限,
(1)求P0的坐标;
(2)若直线
,
且
l
也过切点P0
,求直线l的方程.
19.已知曲线
在点
处的切线方程是
.
(1)求
,
的值;
(2)如果曲线
的某一切线与直线
:
垂直,求切点坐标与切线的方程.
20.已知函数f(x)=
x3-2x2+3x(x∈R)的图象为曲线C.
(1)求过曲线C上任意一点切线斜率的取值范围;
(2)若在曲线C上存在两条相互垂直的切线,求其中一条切线与曲线C的切点的横坐标的取值范围.
答案解析部分
一、单选题
1.【答案】
A
解:B中f′(x0)=
,右边的式子表示函数值的变化量的极限,趋近于0;C中f′(x0)=f(x0+Δx)-f(x0),右边的式子表示函数值的变化量;D中f′(x0)=
,右边的式子表示函数的平均变化率.
故答案为:A
2.【答案】
B
解:当x=5时,y=3,即f(5)=3,又
,
则
,
故答案为:B.
3.【答案】
D
解:因为
,?
,?
因为
处切线斜率为1,所以
,?
,解得
,
故答案为:D.
4.【答案】
D
解:
,设切点横坐标为
,
。
故答案为:D
5.【答案】
B
解:欲判别切线的倾斜角的大小,只须求出其斜率的正负即可,故先利用导数求出在x=4处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决,根据题意,由于
,则可知
,那么可知f’(0)=1,可知该点的切线的斜率为1,可知倾斜角为
。
故答案为:B.
6.【答案】
B
解:由题得
所以
,
。
故答案为:B
7.【答案】
C
解:由题意得,
,由题图易知
,
∴
,
故答案为:C.
8.【答案】
A
解:解:曲线
,
,切点为
,
所以切线
的斜率
,
又直线
过原点,所以
,
得
,
.所以
,故切线
的方程为
即
.
故答案为:A.
9.【答案】
B
解:解:f(x)=x2-2(x>0),则f'(x)=2x(x>0),当x0=2时,f(x0)=2,f'(x0)=4,则切线方程为y-2=4(x-2),
令y=0,则x1=1.5,f(x1)=0.25,f'(x1)=3,则切线方程为y-0.25=3(x-1.5),再令y=0,则x2≈1.417,所以B正确.
故答案为:B
10.【答案】
B
解:由
图象可知,
在
处的切线斜率大于在
处的切线斜率,且斜率为正,
,
,
可看作过
和
的割线的斜率,由图象可知
,
.
故选:
.
11.【答案】
D
解:因为,
,所以,
,即
,由
,所以,
的取值范围是
,故选D。
12.【答案】
D
解:解:探测器与月球表面距离逐渐减小,所以
;
探测器的速度逐渐减小,所以
。
故答案为:D。
二、填空题
13.【答案】
解:因为
=
,
所以
,
则曲线
在点
处的切线斜率为
,即
,
又
所以所求切线的倾斜角
为
.
故答案为:
14.【答案】
2019
解:由题可知:
,则
,
所以
令
,则
,又
,
故
的对称中心为
,故
,
令
所以
所以
,则
故答案为:2019.
15.【答案】
1-ln2
解:对函数
求导得
,对
求导得
,设直线
与曲线
相切于点
,与曲线
相切于点
,则
,由点
在切线上得
,由点
在切线上得
,这两条直线表示同一条直线,所以
,解得
。
16.【答案】
1
解:因为函数
的图像在点
处的切线方程是
,
即
,且
故
故答案为:1
三、解答题
17.【答案】
(1)解:设
,
过点
,
,
在点
处的切线为
且
,
,解得:
,
;
(2)解:
的图象与两坐标轴所围成的图形如下图阴影部分所示,
所求面积
.
18.【答案】
(1)解:由y=x3+x-2,得y′=3x2+1,
由已知得3x2+1=4,解之得x=±1.
当x=1时,y=0;
当x=-1时,y=-4.
又∵点P0在第三象限,
∴切点P0的坐标为(-1,-4);
(2)解:∵直线
l⊥l1
,
l1的斜率为4,
∴直线l的斜率为-1/
4
,
∵l过切点P0
,
点P0的坐标为(-1,-4)
∴直线l的方程为y+4=
(x+1)即x+4y+17=0.
19.【答案】
(1)解:∵
的导数
,
由题意可得
,
,
解得
,
.
(2)解:∵切线与直线
垂直,
∴切线的斜率
.设切点的坐标为
,
则
,∴
.
由
,可得
,或
.
则切线方程为
或
.
即
或
.
20.【答案】
(1)解:由题意得f′(x)=x2-4x+3,则f′(x)=(x-2)2-1≥-1,
即过曲线C上任意一点切线斜率的取值范围是[-1,+∞).
(2)解:设曲线C的其中一条切线的斜率为k,则由(2)中条件并结合(1)中结论可知,
解得-1≤k<0或k≥1,故由-1≤x2-4x+3<0或x2-4x+3≥1,
得x∈(-∞,2-
]∪(1,3)∪[2+
,+∞)
21世纪教育网(www.21cnjy.com)
