2020-2021学年人教版数学八年级下册第二十章:数据的分析 期末复习题(word版含答案)
文档属性
| 名称 | 2020-2021学年人教版数学八年级下册第二十章:数据的分析 期末复习题(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 115.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 07:43:51 | ||
图片预览


文档简介
第二十章:数据的分析 期末复习题
一.选择题(共6小题)
1.数据﹣1,0,3,4,4的平均数是( )
A.4 B.3 C.2.5 D.2
2.八年级(1)班“环保小组”的5位同学组织了一次捡废弃塑料袋的活动,他们捡废弃塑料袋的个数分别为:16,4,6,8,16,这组数据的中位数为( )
A.16 B.8 C.6 D.4
3.永宁县某中学在预防“新冠肺炎”期间,要求学生每日测量体温,九(5)班一名同学连续一周体温情况如表所示:则该名同学这一周体温数据的众数和中位数分别是( )
日期 星期一 星期二 星期三 星期四 星期五 星期六 星期天
体温(℃) 36.2 36.2 36.5 36.3 36.2 36.4 36.3
A.36.3和36.2 B.36.2和36.3 C.36.2和36.2 D.36.2和36.1
4.甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是S甲2=1.2,S乙2=1.1,S丙2=0.6,S丁2=0.9,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
5.下列说法中错误的是( )
A.一组数据的平均数受极端值的影响较大
B.一组数据的平均数、众数、中位数有可能相同
C.如果一组数据的众数是5,那么这组数据中出现次数最多的数据是5
D.一组数据的中位数有时有两个
6.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体平均值为3,中位数为4
B.乙地:总体平均值为2,总体方差为3
C.丙地:中位数为2,众数为3
D.丁地:总体平均值为1,总体方差大于0
二.填空题(共6小题)
7.某学习小组共有学生5人,在一次数学测验中,有2人得85分,2人得90分,1人得70分,该学习小组的平均分为 分.
8.为了解学生暑期在家的阅读情况,随机调查了30名学生某一天的阅读小时数,具体统计如下:
阅读时间(小时) 2 2.5 3 3.5 4
学生人数(名) 1 2 8 16 3
则关于这30名学生阅读小时的众数是 .
9.下面是防“新冠”的医护人员对一辆过往班车的15名乘客测体温的数据:
体温(℃) 36.4 36.5 36.6 36.7 36.8 36.9 37.0
人数(人) 1 1 3 2 3 4 1
这组数据的中位数是 .
10.某校九年级甲、乙两名男生将近期6次立定跳远的平均成绩都是2.2米,方差分别是S甲2=0.004,S乙2=0.006,则两名男生中成绩较稳定的是 (填“甲”或“乙”)
11.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为 .
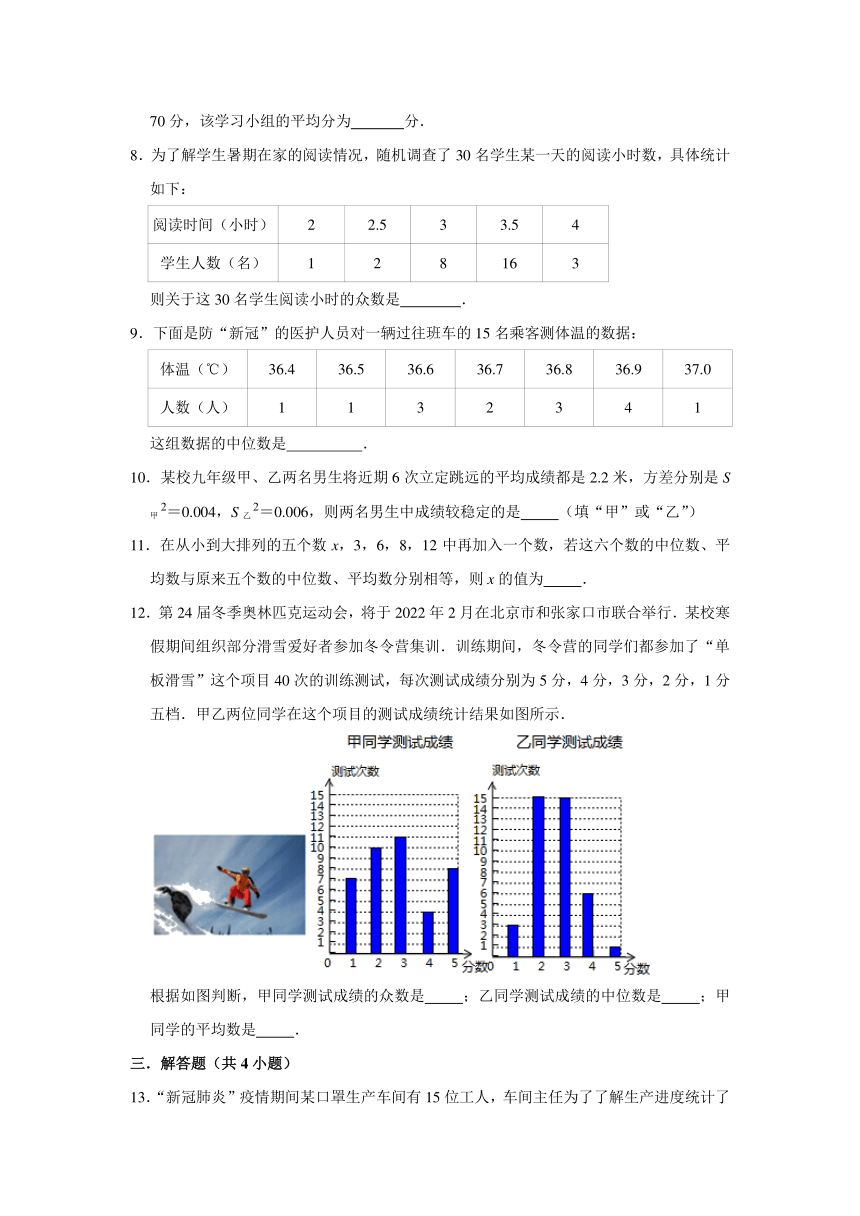
12.第24届冬季奥林匹克运动会,将于2022年2月在北京市和张家口市联合举行.某校寒假期间组织部分滑雪爱好者参加冬令营集训.训练期间,冬令营的同学们都参加了“单板滑雪”这个项目40次的训练测试,每次测试成绩分别为5分,4分,3分,2分,1分五档.甲乙两位同学在这个项目的测试成绩统计结果如图所示.
根据如图判断,甲同学测试成绩的众数是 ;乙同学测试成绩的中位数是 ;甲同学的平均数是 .
三.解答题(共4小题)
13.“新冠肺炎”疫情期间某口罩生产车间有15位工人,车间主任为了了解生产进度统计了15位工人某天生产口罩的个数如表:
每人生产口罩个数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)写出这15位工人该天生产口罩数的平均数、中位数和众数.
(2)假如车间主任把每位工人每天生产口罩个数定为260(个),你认为这个定额是否合理,为什么?
14.受疫情影响,某地无法按原计划正常开学,在延迟开学期间该地区组织了在线教学活动.开学后,某校针对各班在线教学的个性化落实情况,通过初评决定从甲、乙两个班中推荐一个作为在线教学先进班级,下表是这两个班的五项指标(10分制)的考评得分表(单位:分):
班级 课程设置 课程质量 在线答疑 作业情况 学生满意度
甲班 10 10 6 10 7
乙班 10 8 8 9 8
如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2:2:3:1:2的比例确定最终成绩,则应推荐哪个班为在线教学先进班级?
15.A,B两家餐饮店规模相当,国庆假期1~8日的日盈利情况如图所示.
(1)分别求这两家餐饮店国庆假期的日平均盈利;
(2)若A,B两家餐饮店国庆假期的日盈利的方差分别是s2A和s2B,则s2A s2B(填“>”、“=”、“<”).
16.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明
13.3 0.004
李亮 13.3
0.02
(1)张明第2次的成绩为 秒;
(2)张明成绩的平均数为 ;李亮成绩的中位数为 ;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
参考答案与试题解析
一.选择题(共6小题)
1.D; 2.B; 3.B; 4.C; 5.D; 6.B;
二.填空题(共6小题)
7.84; 8.3.5; 9.36.8℃; 10.甲; 11.1; 12.3;3;2.9;
三.解答题(共4小题)
13.【解答】解:(1)这15位工人该天生产口罩数的平均数==260;
把这15位工人该天生产口罩数从小到大排列,处于中间位置的是第8个数,所以中位数是240;
这15位工人该天生产口罩数中,240出现的次数最多,所以众数是240;
(2)不合理,因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性,因为240既是中位数,又是众数,是大多数人能达到的定额,故定额为240较为合理.
14.【解答】解:甲班:=8.2(分);
乙班:=8.5(分);
∵8.2<8.5,
∴应推荐乙班为在线教学先进班级.
15.【解答】解:(1)A餐饮店的平均盈利是:=6.5(万元),
B餐饮店的平均盈利是:=6.4(万元);
(2)根据折线统计图的波动情况可以看出,s2A<s2B;
故答案为:<.
16.【解答】解:(1)张明第2次的成绩为13.4秒;
(2)张明成绩的平均数为=13.3(秒);李亮成绩的中位数为13.3(秒);
故答案为13.4;13.3秒,13.3秒;
(3)选择张明,平均数和中位数相同,但张明成绩的方差小于李亮成绩的方差,所以张明成绩比李亮成绩稳定,因此选择张明.
一.选择题(共6小题)
1.数据﹣1,0,3,4,4的平均数是( )
A.4 B.3 C.2.5 D.2
2.八年级(1)班“环保小组”的5位同学组织了一次捡废弃塑料袋的活动,他们捡废弃塑料袋的个数分别为:16,4,6,8,16,这组数据的中位数为( )
A.16 B.8 C.6 D.4
3.永宁县某中学在预防“新冠肺炎”期间,要求学生每日测量体温,九(5)班一名同学连续一周体温情况如表所示:则该名同学这一周体温数据的众数和中位数分别是( )
日期 星期一 星期二 星期三 星期四 星期五 星期六 星期天
体温(℃) 36.2 36.2 36.5 36.3 36.2 36.4 36.3
A.36.3和36.2 B.36.2和36.3 C.36.2和36.2 D.36.2和36.1
4.甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是S甲2=1.2,S乙2=1.1,S丙2=0.6,S丁2=0.9,则射击成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
5.下列说法中错误的是( )
A.一组数据的平均数受极端值的影响较大
B.一组数据的平均数、众数、中位数有可能相同
C.如果一组数据的众数是5,那么这组数据中出现次数最多的数据是5
D.一组数据的中位数有时有两个
6.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )
A.甲地:总体平均值为3,中位数为4
B.乙地:总体平均值为2,总体方差为3
C.丙地:中位数为2,众数为3
D.丁地:总体平均值为1,总体方差大于0
二.填空题(共6小题)
7.某学习小组共有学生5人,在一次数学测验中,有2人得85分,2人得90分,1人得70分,该学习小组的平均分为 分.
8.为了解学生暑期在家的阅读情况,随机调查了30名学生某一天的阅读小时数,具体统计如下:
阅读时间(小时) 2 2.5 3 3.5 4
学生人数(名) 1 2 8 16 3
则关于这30名学生阅读小时的众数是 .
9.下面是防“新冠”的医护人员对一辆过往班车的15名乘客测体温的数据:
体温(℃) 36.4 36.5 36.6 36.7 36.8 36.9 37.0
人数(人) 1 1 3 2 3 4 1
这组数据的中位数是 .
10.某校九年级甲、乙两名男生将近期6次立定跳远的平均成绩都是2.2米,方差分别是S甲2=0.004,S乙2=0.006,则两名男生中成绩较稳定的是 (填“甲”或“乙”)
11.在从小到大排列的五个数x,3,6,8,12中再加入一个数,若这六个数的中位数、平均数与原来五个数的中位数、平均数分别相等,则x的值为 .
12.第24届冬季奥林匹克运动会,将于2022年2月在北京市和张家口市联合举行.某校寒假期间组织部分滑雪爱好者参加冬令营集训.训练期间,冬令营的同学们都参加了“单板滑雪”这个项目40次的训练测试,每次测试成绩分别为5分,4分,3分,2分,1分五档.甲乙两位同学在这个项目的测试成绩统计结果如图所示.
根据如图判断,甲同学测试成绩的众数是 ;乙同学测试成绩的中位数是 ;甲同学的平均数是 .
三.解答题(共4小题)
13.“新冠肺炎”疫情期间某口罩生产车间有15位工人,车间主任为了了解生产进度统计了15位工人某天生产口罩的个数如表:
每人生产口罩个数 540 450 300 240 210 120
人数 1 1 2 6 3 2
(1)写出这15位工人该天生产口罩数的平均数、中位数和众数.
(2)假如车间主任把每位工人每天生产口罩个数定为260(个),你认为这个定额是否合理,为什么?
14.受疫情影响,某地无法按原计划正常开学,在延迟开学期间该地区组织了在线教学活动.开学后,某校针对各班在线教学的个性化落实情况,通过初评决定从甲、乙两个班中推荐一个作为在线教学先进班级,下表是这两个班的五项指标(10分制)的考评得分表(单位:分):
班级 课程设置 课程质量 在线答疑 作业情况 学生满意度
甲班 10 10 6 10 7
乙班 10 8 8 9 8
如果学校把“课程设置”、“课程质量”、“在线答疑”、“作业情况”、“学生满意度”这五项指标得分按照2:2:3:1:2的比例确定最终成绩,则应推荐哪个班为在线教学先进班级?
15.A,B两家餐饮店规模相当,国庆假期1~8日的日盈利情况如图所示.
(1)分别求这两家餐饮店国庆假期的日平均盈利;
(2)若A,B两家餐饮店国庆假期的日盈利的方差分别是s2A和s2B,则s2A s2B(填“>”、“=”、“<”).
16.学校为了让同学们走向操场、积极参加体育锻炼,启动了“学生阳光体育运动”,张明和李亮在体育运动中报名参加了百米训练小组.在近几次百米训练中,教练对他们两人的测试成绩进行了统计和分析,请根据图表中的信息解答以下问题:
平均数 中位数 方差
张明
13.3 0.004
李亮 13.3
0.02
(1)张明第2次的成绩为 秒;
(2)张明成绩的平均数为 ;李亮成绩的中位数为 ;
(3)现在从张明和李亮中选择一名成绩优秀的去参加比赛,若你是他们的教练,应该选择谁?请说明理由.
参考答案与试题解析
一.选择题(共6小题)
1.D; 2.B; 3.B; 4.C; 5.D; 6.B;
二.填空题(共6小题)
7.84; 8.3.5; 9.36.8℃; 10.甲; 11.1; 12.3;3;2.9;
三.解答题(共4小题)
13.【解答】解:(1)这15位工人该天生产口罩数的平均数==260;
把这15位工人该天生产口罩数从小到大排列,处于中间位置的是第8个数,所以中位数是240;
这15位工人该天生产口罩数中,240出现的次数最多,所以众数是240;
(2)不合理,因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性,因为240既是中位数,又是众数,是大多数人能达到的定额,故定额为240较为合理.
14.【解答】解:甲班:=8.2(分);
乙班:=8.5(分);
∵8.2<8.5,
∴应推荐乙班为在线教学先进班级.
15.【解答】解:(1)A餐饮店的平均盈利是:=6.5(万元),
B餐饮店的平均盈利是:=6.4(万元);
(2)根据折线统计图的波动情况可以看出,s2A<s2B;
故答案为:<.
16.【解答】解:(1)张明第2次的成绩为13.4秒;
(2)张明成绩的平均数为=13.3(秒);李亮成绩的中位数为13.3(秒);
故答案为13.4;13.3秒,13.3秒;
(3)选择张明,平均数和中位数相同,但张明成绩的方差小于李亮成绩的方差,所以张明成绩比李亮成绩稳定,因此选择张明.
