2020-2021学年湘教新版八年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年湘教新版八年级下册数学期末练习试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 249.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 08:19:27 | ||
图片预览




文档简介
2020-2021学年湘教新版八年级下册数学期末练习试题
一.选择题(共8小题,满分24分,每小题3分)
1.函数y=+(x﹣5)﹣2中自变量x的取值范围是( )
A.x≥3且x≠5
B.x>3且x≠5
C.x<3且x≠5
D.x≤3且x≠5
2.有40个数据,共分成6组,第1﹣4组的频数分别是10,5,7,6,第5组的频率为0.10,则第6组的频率为( )
A.0.25
B.0.30
C.0.15
D.0.20
3.已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A.3
B.6
C.8
D.5
4.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为( )
A.y=x
B.y=6x
C.y=6x2
D.y=
5.如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
A.6cm
B.4cm
C.3cm
D.2cm
6.对于函数y=﹣2x+1,下列结论正确的是( )
A.y值随x值的增大而增大
B.它的图象与x轴交点坐标为(0,1)
C.它的图象必经过点(﹣1,3)
D.它的图象经过第一、二、三象限
7.如图,正六边形ABCDEF的边长为6,且点O为正六边形的中心,将半径为的⊙M沿六边形作逆时针滚动,连接OM,过点M作MP⊥OM,并且OM=MP,连接OP,则在⊙M滚动的过程中,Rt△OMP面积的最大值是( )
A.2
B.
C.16
D.8
8.一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米:
②出发1小时,货车与小汽车相遇;
③出发1.5小时,小汽车比货车多行驶了60千米;
④小汽车的速度是货车速度的2倍.
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,满分24分,每小题3分)
9.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、13,第五组的频率是0.1,那么第六组的频数是
.
10.一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
x/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
根据表格中水位的变化规律,则y与x的函数表达式为
.
11.已知点P(﹣2,a)在一次函数y=3x+1的图象上,则a=
.
12.新定义[a,b]为一次函数(其中a≠0,且a,b为实数)的“关联数”,若“关联数”[3,m+2]所对应的一次函数是正比例函数,则关于x的方程+=1的解为
.
13.如图,直线EF经过平行四边形ABCD的对角线的交点O,若四边形AEFB的面积为100cm2,则四边形EDCF的面积为
cm2.
14.在平面直角坐标系中,将点A(﹣1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是
.
15.把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为
.
16.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3,AB=10,则△ABD的面积是
.
三.解答题(共7小题,满分52分)
17.已知一次函数图象经过(3,5)和(﹣4,﹣9)两点.
(1)求此一次函数的解析式;
(2)若点(m,2)在函数图象上,求m的值.
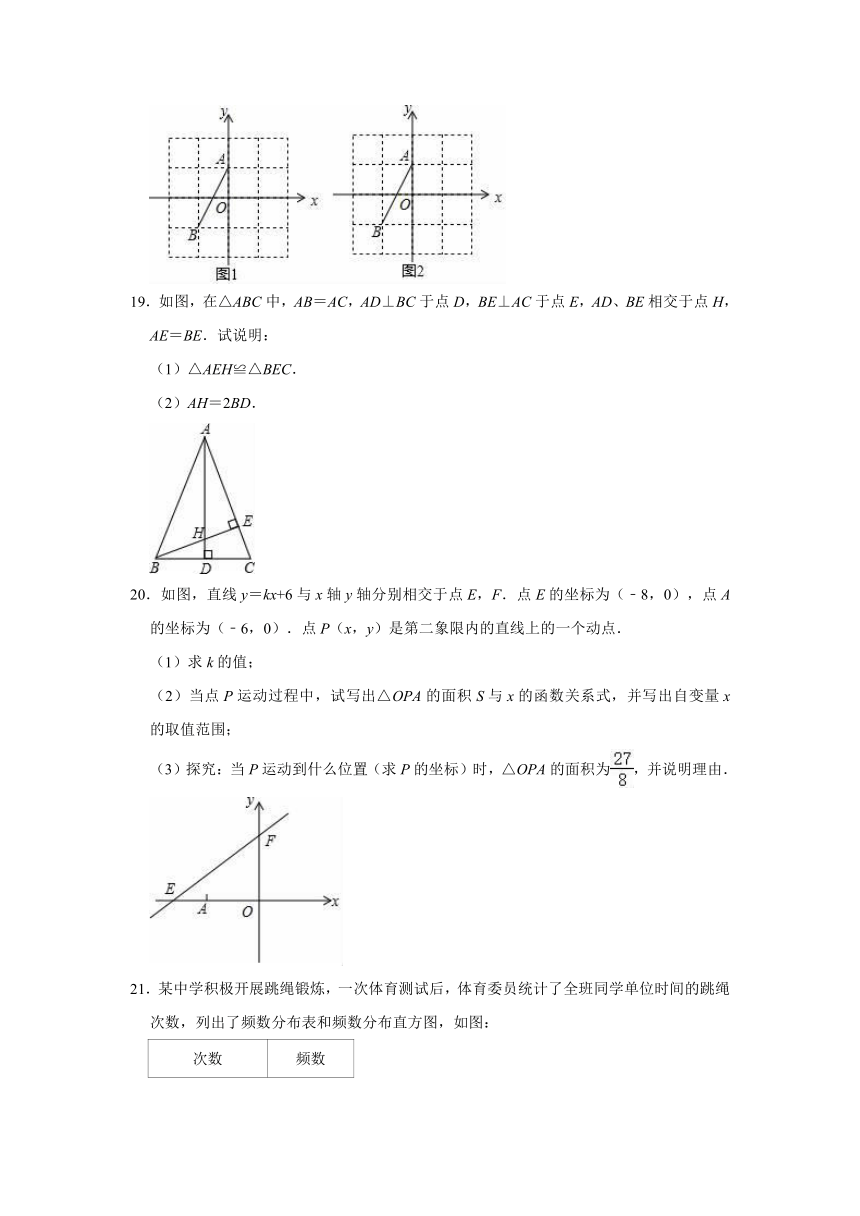
18.在4×4的正方形网格中建立如图1、2所示的直角坐标系,其中格点A,B的坐标分别是(0,1),(﹣1,﹣1).(1)请图1中添加一个格点C,使得△ABC是轴对称图形,且对称轴经过点(0,﹣1).
(2)请图2中添加一个格点D,使得△ABD也是轴对称图形,且对称轴经过点(1,1).
19.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:
(1)△AEH≌△BEC.
(2)AH=2BD.
20.如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).点P(x,y)是第二象限内的直线上的一个动点.
(1)求k的值;
(2)当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置(求P的坐标)时,△OPA的面积为,并说明理由.
21.某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和频数分布直方图,如图:
次数
频数
60≤x<80
80≤x<100
4
100≤x<120
18
120≤x<140
13
140≤x<160
8
160≤x<180
180≤x<200
1
(1)补全频数分布表和频数分布直方图.
(2)表中组距是
次,组数是
组.
(3)跳绳次数在100≤x<140范围的学生有
人,全班共有
人.
(4)若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
22.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中
(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是
米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
23.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G连接DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求的值.
参考答案与试题解析
一.选择题(共8小题,满分24分,每小题3分)
1.解:依题意有x﹣3>0且x﹣5≠0,
解得:x>3且x≠5.
故选:B.
2.解:∵第5组的频率为0.10,
∴第5组的频数为40×0.1=4,
∴第6组的频数为40﹣(10+5+7+6+4)=8,
故第6组的频率为=0.2.
故选:D.
3.解:设两直角边分别为3x,4x.
由勾股定理得(3x)2+(4x)2=100.
解得x=2.则3x=3×2=6,4x=4×2=8.
∴直角三角形的两直角边的长分别为6,8.
较短直角边的长为6.
故选:B.
4.解:由题意得,y=6x2,
故选:C.
5.解:∵四边形ABCD是菱形,
∴AD=BC=6cm,AC⊥BD,
∵H为AD边的中点,
∴HO=AD=3cm.
故选:C.
6.解:A、∵k=﹣2<0,
∴y值随x值的增大而减小,结论A不符合题意;
B、当y=0时,﹣2x+1=0,解得:x=,
∴函数y=﹣2x+1的图象与x轴交点坐标为(,0),结论B不符合题意;
C、当x=﹣1时,y=﹣2x+1=3,
∴函数y=﹣2x+1的图象必经过点(﹣1,3),结论C符合题意;
D、∵k=﹣2<0,b=1>0,
∴函数y=﹣2x+1的图象经过第一、二、四象限,结论D不符合题意.
故选:C.
7.解:如图,当⊙M与正六边形的两边AB、BC相切时,OM的值最大,设⊙M与AB相切于点N,连接MN,OA.
∵△OAB是等边三角形,
∴OB=AB=6,∠MBN=60°,
在Rt△MNB中,∵MN=,∠NMB=30°,
∴BN=1,BM=2,
∴OM=MP=4,
∴Rt△OMP面积的最大值=×4×4=8,
故选:D.
8.解:(1)由图象可知,当t=0时,即货车、汽车分别在A、B两地,s=120,
所以A、B两地相距120千米,故①错误;
(2)当t=1时,s=0,表示出发1小时,货车与小汽车相遇,故②正确;
(3)根据图象知,汽车行驶1.5小时达到终点A地,货车行驶3小时到达终点B地,
故货车的速度为:120÷3=40(千米/小时),
出发1.5小时货车行驶的路程为:1.5×40=60(千米),
小汽车行驶1.5小时达到终点A地,即小汽车1.5小时行驶路程为120千米,
故出发1.5小时,小汽车比货车多行驶了60千米,故③正确;
(4)∵由(3)知小汽车的速度为:120÷1.5=80(千米/小时),货车的速度为40(千米/小时),
∴小汽车的速度是货车速度的2倍,故④正确.
∴正确的有②③④三个.
故选:C.
二.填空题(共8小题,满分24分,每小题3分)
9.解:根据题意,得:第一组到第四组的频率和是=0.875,
又∵第五组的频率是0.1,
∴第六组的频率为1﹣(0.875+0.1)=0.025,
∴第六组的频数为:40×0.025=1.
故答案为:1.
10.解:设y与x的函数表达式为y=kx+b,由记录表得:
,
解得:.
故y与x的函数表达式为y=0.3x+3.
故答案为:y=0.3x+3.
11.解:∵点P(﹣2,a)在一次函数y=3x+1的图象上,
∴a=3×(﹣2)+1=﹣5.
故答案是:﹣5.
12.解:根据“关联数”[3,m+2]所对应的一次函数是正比例函数,
得到y=3x+m+2为正比例函数,即m+2=0,
解得:m=﹣2,
则分式方程为﹣=1,
去分母得:2﹣(x﹣1)=2(x﹣1),
去括号得:2﹣x+1=2x﹣2,
解得:x=,
经检验x=是分式方程的解.
故答案为:x=.
13.解:连接AC,BD,
∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO.
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
同理可得△AOB≌△COD,△BOF≌△DOE,
∴S四边形EDCF=S四边形AEFB=100(cm2).
故答案为:100.
14.解:点A(﹣1,2)向右平移3个单位长度得到的B的坐标为(﹣1+3,2),即(2,2),
则点B关于x轴的对称点C的坐标是(2,﹣2),
故答案为:(2,﹣2).
15.解:把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为:y=﹣(x﹣1)﹣1=﹣x.
故答案为:y=﹣x.
16.解:如图,作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=3,
∴△ABD的面积=×AB×DE=×10×3=15,
故答案为:15.
三.解答题(共7小题,满分52分)
17.解:(1)设一次函数的解析式为y=kx+b,
则有,
解得:,
∴一次函数的解析式为y=2x﹣1;
(2)∵点(m,2)在一次函数y=2x﹣1图象上
∴2m﹣1=2,
∴m=.
18.解:(1)如图,点C即为所求.
(2)如图,点D即为所求.
19.解:(1)∵AD⊥BC,
∴∠DAC+∠C=90°,
∵BE⊥AC,
∴∠EBC+∠C=90°,
∴∠DAC=∠EBC,
在△AEH与△BEC中,
,
∴△AEH≌△BEC(ASA);
(2)∵△AEH≌△BEC,
∴AH=BC,
∵AB=AC,AD⊥BC,
∴BC=2BD,
∴AH=2BD.
20.解:(1)把E(﹣8,0)代入直线解析式得:0=﹣8k+6,
解得:k=;
(2)根据题意得:S=OA?|yP纵坐标|=×6×y=3y,
把P(x,y)代入解析式得:y=x+6,
则S=x+18(﹣8<x<0);
(3)令S=,得到x+18=,
解得:x=﹣,
此时P坐标为(﹣,).
21.解:(1)如图,成绩在60≤x<80的人数为2人,成绩在160≤x<180的人数为4人,
(2)表中组距是20次,组数是7组.
(3)跳绳次数在100≤x<140范围的学生有31人,全班人数为2+4+18+13+8+4+1=50(人);
故答案为2,4;20,7;31,50;
(4)跳绳次数不低于140次的人数为8+4+1=13,
所以全班同学跳绳的优秀率=×100%=26%.
22.解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻,
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
由图象可知:赛跑的全过程为1500米;
故答案为:兔子,1500;
(2)结合图象得出:
兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).
(3)700÷30=(分钟),
所以乌龟用了分钟追上了正在睡觉的兔子.
(4)∵兔子跑了700米停下睡觉,用了2分钟,
∴剩余800米,所用的时间为:800÷400=2(分钟),
∴兔子睡觉用了:50.5﹣2﹣2=46.5(分钟).
所以兔子中间停下睡觉用了46.5分钟.
23.(1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,
∵FG∥CD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴FG=FE,
∴DG=GF=EF=DE,
∴四边形DEFG为菱形;
(2)设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,
在Rt△EFC中,FC2+EC2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,CE=8﹣x=3,
∴.
一.选择题(共8小题,满分24分,每小题3分)
1.函数y=+(x﹣5)﹣2中自变量x的取值范围是( )
A.x≥3且x≠5
B.x>3且x≠5
C.x<3且x≠5
D.x≤3且x≠5
2.有40个数据,共分成6组,第1﹣4组的频数分别是10,5,7,6,第5组的频率为0.10,则第6组的频率为( )
A.0.25
B.0.30
C.0.15
D.0.20
3.已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A.3
B.6
C.8
D.5
4.正方体的棱长为x,表面积为y,则y与x之间的函数关系式为( )
A.y=x
B.y=6x
C.y=6x2
D.y=
5.如图,菱形ABCD中,对角线AC与BD相交于点O,H为AD边的中点,BC=6cm,则OH的长为( )
A.6cm
B.4cm
C.3cm
D.2cm
6.对于函数y=﹣2x+1,下列结论正确的是( )
A.y值随x值的增大而增大
B.它的图象与x轴交点坐标为(0,1)
C.它的图象必经过点(﹣1,3)
D.它的图象经过第一、二、三象限
7.如图,正六边形ABCDEF的边长为6,且点O为正六边形的中心,将半径为的⊙M沿六边形作逆时针滚动,连接OM,过点M作MP⊥OM,并且OM=MP,连接OP,则在⊙M滚动的过程中,Rt△OMP面积的最大值是( )
A.2
B.
C.16
D.8
8.一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
①A、B两地相距60千米:
②出发1小时,货车与小汽车相遇;
③出发1.5小时,小汽车比货车多行驶了60千米;
④小汽车的速度是货车速度的2倍.
A.1个
B.2个
C.3个
D.4个
二.填空题(共8小题,满分24分,每小题3分)
9.已知一个40个数据的样本,把它分成6组,第一组到第四组的频数分别是10、5、7、13,第五组的频率是0.1,那么第六组的频数是
.
10.一个水库的水位在最近5h内持续上涨.下表记录了这5h内6个时间点的水位高度,其中x表示时间,y表示水位高度.
x/h
0
1
2
3
4
5
y/m
3
3.3
3.6
3.9
4.2
4.5
根据表格中水位的变化规律,则y与x的函数表达式为
.
11.已知点P(﹣2,a)在一次函数y=3x+1的图象上,则a=
.
12.新定义[a,b]为一次函数(其中a≠0,且a,b为实数)的“关联数”,若“关联数”[3,m+2]所对应的一次函数是正比例函数,则关于x的方程+=1的解为
.
13.如图,直线EF经过平行四边形ABCD的对角线的交点O,若四边形AEFB的面积为100cm2,则四边形EDCF的面积为
cm2.
14.在平面直角坐标系中,将点A(﹣1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是
.
15.把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为
.
16.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=3,AB=10,则△ABD的面积是
.
三.解答题(共7小题,满分52分)
17.已知一次函数图象经过(3,5)和(﹣4,﹣9)两点.
(1)求此一次函数的解析式;
(2)若点(m,2)在函数图象上,求m的值.
18.在4×4的正方形网格中建立如图1、2所示的直角坐标系,其中格点A,B的坐标分别是(0,1),(﹣1,﹣1).(1)请图1中添加一个格点C,使得△ABC是轴对称图形,且对称轴经过点(0,﹣1).
(2)请图2中添加一个格点D,使得△ABD也是轴对称图形,且对称轴经过点(1,1).
19.如图,在△ABC中,AB=AC,AD⊥BC于点D,BE⊥AC于点E,AD、BE相交于点H,AE=BE.试说明:
(1)△AEH≌△BEC.
(2)AH=2BD.
20.如图,直线y=kx+6与x轴y轴分别相交于点E,F.点E的坐标为(﹣8,0),点A的坐标为(﹣6,0).点P(x,y)是第二象限内的直线上的一个动点.
(1)求k的值;
(2)当点P运动过程中,试写出△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(3)探究:当P运动到什么位置(求P的坐标)时,△OPA的面积为,并说明理由.
21.某中学积极开展跳绳锻炼,一次体育测试后,体育委员统计了全班同学单位时间的跳绳次数,列出了频数分布表和频数分布直方图,如图:
次数
频数
60≤x<80
80≤x<100
4
100≤x<120
18
120≤x<140
13
140≤x<160
8
160≤x<180
180≤x<200
1
(1)补全频数分布表和频数分布直方图.
(2)表中组距是
次,组数是
组.
(3)跳绳次数在100≤x<140范围的学生有
人,全班共有
人.
(4)若规定跳绳次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
22.“龟兔赛跑”的故事同学们都非常熟悉,图中的线段OD和折线OABC表示“龟兔赛跑时路程与时间的关系,请你根据图中给出的信息,解决下列问题.
(1)填空:折线OABC表示赛跑过程中
(填“兔子”或“乌龟”)的路程与时间的关系,赛跑的全过程是
米.
(2)兔子在起初每分钟跑多少米?乌龟每分钟爬多少米?
(3)乌龟用了多少分钟追上了正在睡觉的兔子?
(4)兔子醒来后,以400米/分的速度跑向终点,结果还是比乌龟晚到了0.5分钟,请你算算兔子中间停下睡觉用了多少分钟.
23.如图,在矩形ABCD中,点E在边CD上,将该矩形沿AE折叠,使点D落在边BC上的点F处,过点F作FG∥CD,交AE于点G连接DG.
(1)求证:四边形DEFG为菱形;
(2)若CD=8,CF=4,求的值.
参考答案与试题解析
一.选择题(共8小题,满分24分,每小题3分)
1.解:依题意有x﹣3>0且x﹣5≠0,
解得:x>3且x≠5.
故选:B.
2.解:∵第5组的频率为0.10,
∴第5组的频数为40×0.1=4,
∴第6组的频数为40﹣(10+5+7+6+4)=8,
故第6组的频率为=0.2.
故选:D.
3.解:设两直角边分别为3x,4x.
由勾股定理得(3x)2+(4x)2=100.
解得x=2.则3x=3×2=6,4x=4×2=8.
∴直角三角形的两直角边的长分别为6,8.
较短直角边的长为6.
故选:B.
4.解:由题意得,y=6x2,
故选:C.
5.解:∵四边形ABCD是菱形,
∴AD=BC=6cm,AC⊥BD,
∵H为AD边的中点,
∴HO=AD=3cm.
故选:C.
6.解:A、∵k=﹣2<0,
∴y值随x值的增大而减小,结论A不符合题意;
B、当y=0时,﹣2x+1=0,解得:x=,
∴函数y=﹣2x+1的图象与x轴交点坐标为(,0),结论B不符合题意;
C、当x=﹣1时,y=﹣2x+1=3,
∴函数y=﹣2x+1的图象必经过点(﹣1,3),结论C符合题意;
D、∵k=﹣2<0,b=1>0,
∴函数y=﹣2x+1的图象经过第一、二、四象限,结论D不符合题意.
故选:C.
7.解:如图,当⊙M与正六边形的两边AB、BC相切时,OM的值最大,设⊙M与AB相切于点N,连接MN,OA.
∵△OAB是等边三角形,
∴OB=AB=6,∠MBN=60°,
在Rt△MNB中,∵MN=,∠NMB=30°,
∴BN=1,BM=2,
∴OM=MP=4,
∴Rt△OMP面积的最大值=×4×4=8,
故选:D.
8.解:(1)由图象可知,当t=0时,即货车、汽车分别在A、B两地,s=120,
所以A、B两地相距120千米,故①错误;
(2)当t=1时,s=0,表示出发1小时,货车与小汽车相遇,故②正确;
(3)根据图象知,汽车行驶1.5小时达到终点A地,货车行驶3小时到达终点B地,
故货车的速度为:120÷3=40(千米/小时),
出发1.5小时货车行驶的路程为:1.5×40=60(千米),
小汽车行驶1.5小时达到终点A地,即小汽车1.5小时行驶路程为120千米,
故出发1.5小时,小汽车比货车多行驶了60千米,故③正确;
(4)∵由(3)知小汽车的速度为:120÷1.5=80(千米/小时),货车的速度为40(千米/小时),
∴小汽车的速度是货车速度的2倍,故④正确.
∴正确的有②③④三个.
故选:C.
二.填空题(共8小题,满分24分,每小题3分)
9.解:根据题意,得:第一组到第四组的频率和是=0.875,
又∵第五组的频率是0.1,
∴第六组的频率为1﹣(0.875+0.1)=0.025,
∴第六组的频数为:40×0.025=1.
故答案为:1.
10.解:设y与x的函数表达式为y=kx+b,由记录表得:
,
解得:.
故y与x的函数表达式为y=0.3x+3.
故答案为:y=0.3x+3.
11.解:∵点P(﹣2,a)在一次函数y=3x+1的图象上,
∴a=3×(﹣2)+1=﹣5.
故答案是:﹣5.
12.解:根据“关联数”[3,m+2]所对应的一次函数是正比例函数,
得到y=3x+m+2为正比例函数,即m+2=0,
解得:m=﹣2,
则分式方程为﹣=1,
去分母得:2﹣(x﹣1)=2(x﹣1),
去括号得:2﹣x+1=2x﹣2,
解得:x=,
经检验x=是分式方程的解.
故答案为:x=.
13.解:连接AC,BD,
∵四边形ABCD是平行四边形,
∴OA=OC,AD∥BC,
∴∠EAO=∠FCO.
在△AOE与△COF中,
,
∴△AOE≌△COF(ASA),
同理可得△AOB≌△COD,△BOF≌△DOE,
∴S四边形EDCF=S四边形AEFB=100(cm2).
故答案为:100.
14.解:点A(﹣1,2)向右平移3个单位长度得到的B的坐标为(﹣1+3,2),即(2,2),
则点B关于x轴的对称点C的坐标是(2,﹣2),
故答案为:(2,﹣2).
15.解:把直线y=﹣x﹣1沿x轴向右平移1个单位长度,所得直线的函数解析式为:y=﹣(x﹣1)﹣1=﹣x.
故答案为:y=﹣x.
16.解:如图,作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,DE⊥AB,
∴DE=DC=3,
∴△ABD的面积=×AB×DE=×10×3=15,
故答案为:15.
三.解答题(共7小题,满分52分)
17.解:(1)设一次函数的解析式为y=kx+b,
则有,
解得:,
∴一次函数的解析式为y=2x﹣1;
(2)∵点(m,2)在一次函数y=2x﹣1图象上
∴2m﹣1=2,
∴m=.
18.解:(1)如图,点C即为所求.
(2)如图,点D即为所求.
19.解:(1)∵AD⊥BC,
∴∠DAC+∠C=90°,
∵BE⊥AC,
∴∠EBC+∠C=90°,
∴∠DAC=∠EBC,
在△AEH与△BEC中,
,
∴△AEH≌△BEC(ASA);
(2)∵△AEH≌△BEC,
∴AH=BC,
∵AB=AC,AD⊥BC,
∴BC=2BD,
∴AH=2BD.
20.解:(1)把E(﹣8,0)代入直线解析式得:0=﹣8k+6,
解得:k=;
(2)根据题意得:S=OA?|yP纵坐标|=×6×y=3y,
把P(x,y)代入解析式得:y=x+6,
则S=x+18(﹣8<x<0);
(3)令S=,得到x+18=,
解得:x=﹣,
此时P坐标为(﹣,).
21.解:(1)如图,成绩在60≤x<80的人数为2人,成绩在160≤x<180的人数为4人,
(2)表中组距是20次,组数是7组.
(3)跳绳次数在100≤x<140范围的学生有31人,全班人数为2+4+18+13+8+4+1=50(人);
故答案为2,4;20,7;31,50;
(4)跳绳次数不低于140次的人数为8+4+1=13,
所以全班同学跳绳的优秀率=×100%=26%.
22.解:(1)∵乌龟是一直跑的而兔子中间有休息的时刻,
∴折线OABC表示赛跑过程中兔子的路程与时间的关系;
由图象可知:赛跑的全过程为1500米;
故答案为:兔子,1500;
(2)结合图象得出:
兔子在起初每分钟跑700÷2=350(米),乌龟每分钟爬1500÷50=30(米).
(3)700÷30=(分钟),
所以乌龟用了分钟追上了正在睡觉的兔子.
(4)∵兔子跑了700米停下睡觉,用了2分钟,
∴剩余800米,所用的时间为:800÷400=2(分钟),
∴兔子睡觉用了:50.5﹣2﹣2=46.5(分钟).
所以兔子中间停下睡觉用了46.5分钟.
23.(1)证明:由折叠的性质可知:DG=FG,ED=EF,∠1=∠2,
∵FG∥CD,
∴∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴FG=FE,
∴DG=GF=EF=DE,
∴四边形DEFG为菱形;
(2)设DE=x,根据折叠的性质,EF=DE=x,EC=8﹣x,
在Rt△EFC中,FC2+EC2=EF2,
即42+(8﹣x)2=x2,
解得:x=5,CE=8﹣x=3,
∴.
同课章节目录
