2021年 人教版 七年级下册数学 10.2 直方图 同步课时练习卷(Word版 含解析)
文档属性
| 名称 | 2021年 人教版 七年级下册数学 10.2 直方图 同步课时练习卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 192.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 07:01:20 | ||
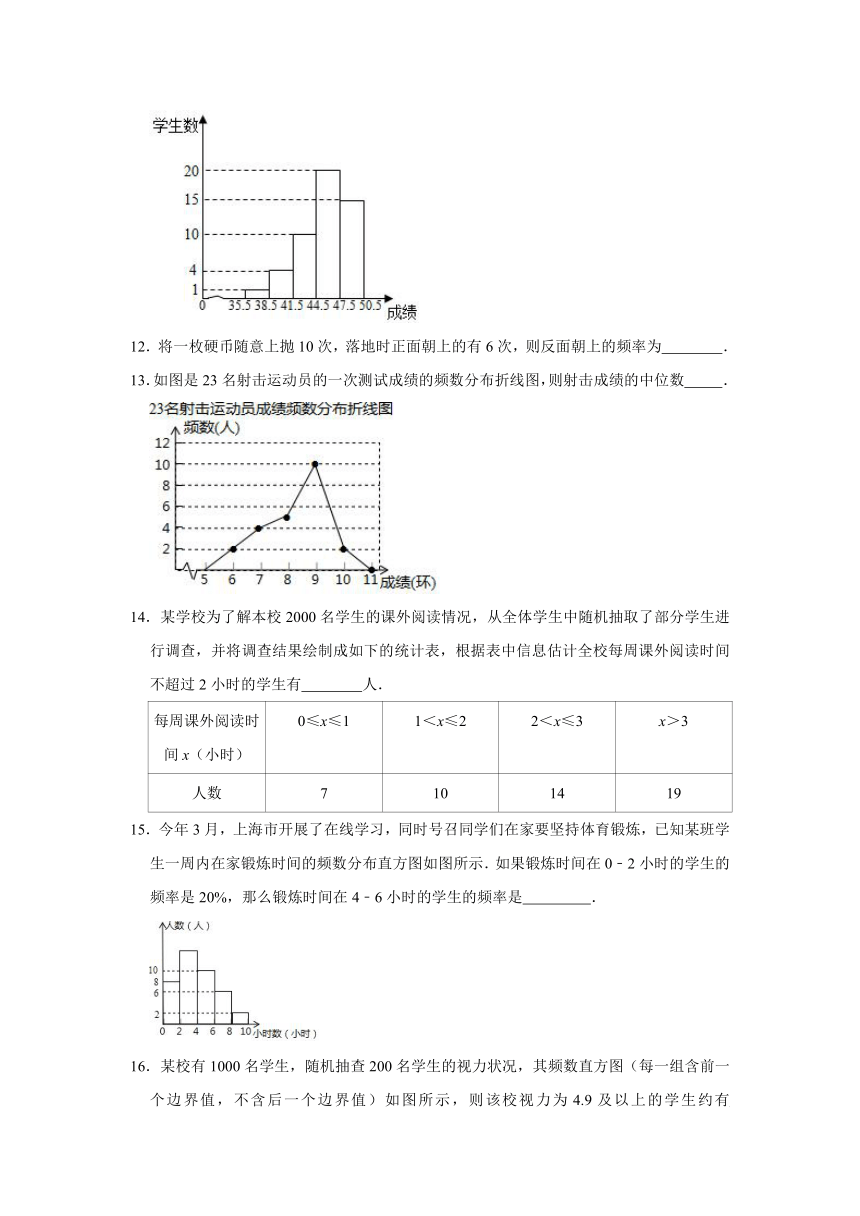
图片预览




文档简介
2021年人教版七年级下册数学10.2《直方图》同步课时练习卷
一.选择题
1.在一个样本中,50个数据分别落在5个小组内,第1、2、3、5小组数据的个数分别是2、8、15、5,则第4小组的频率是( )
A.0.6 B.20 C.0.4 D.30
2.下列说法错误的是( )
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件A试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
3.对一批衬衣进行抽检,得到合格衬衣的频数表如下,若出售1200件衬衣,则其中次品的件数大约是( )
抽取件数(件) 50 100 150 200 500 800 1000
合格频数 48 98 144 193 489 784 981
A.12 B.24 C.1188 D.1176
4.为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
5.某公路上的测速仪,在某一时间段内测得30辆汽车的速度(单位:km/h),其最大值和最小值分别是80,56.为了制作频数直方图,以5为组距,这样,可以把数据分成( )
A.4组 B.5组 C.6组 D.10组
6.某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
C.掷一个质地均匀的正六面体骰子,向上的面点数是4
D.掷一枚一元硬币,落地后正面朝上
7.在一组数据中,最大值是17,最小值是6,绘制频数分布表时,如果取组距为2,那么应分成( )组.
A.3 B.4 C.5 D.6
8.将40个数据分成五组,编成组号为①~⑤的五个组,频数分布如表:
组号 ① ② ③ ④ ⑤
频数 12 4 6
10
则第4组的频率是( )
A.0.2 B.0.3 C.8 D.12
二.填空题
9.一次射击训练中,李磊共射击10发,射中8环的频率是0.4,则射中8环的频数是 .
10.将一个有80个数据的样本经统计分成6组,若某一组的频率为0.15,则该组的频数为 .
11.2020年綦江区中招体考已结束,数据显示,与去年相比,体考成绩略有下滑.今年某中学某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在44.5~47.5分范围内为良好,则该班学生体育成绩良好的百分率是 .
12.将一枚硬币随意上抛10次,落地时正面朝上的有6次,则反面朝上的频率为 .
13.如图是23名射击运动员的一次测试成绩的频数分布折线图,则射击成绩的中位数 .
14.某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
15.今年3月,上海市开展了在线学习,同时号召同学们在家要坚持体育锻炼,已知某班学生一周内在家锻炼时间的频数分布直方图如图所示.如果锻炼时间在0﹣2小时的学生的频率是20%,那么锻炼时间在4﹣6小时的学生的频率是 .
16.某校有1000名学生,随机抽查200名学生的视力状况,其频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,则该校视力为4.9及以上的学生约有 人.
三.解答题
17.八甲班进行了一次数学考试,将成绩绘制成了如下不完整的频数分布表和频数直方图:
(1)求频数分布表中a和b的值;
(2)将频数直方图补充完整;
(3)成绩不低于60分为及格,该班本次数学考试的及格率是多少?
成绩 频数(人数) 频率
50≤x<60 5 0.1
60≤x<70 10 0.2
70≤x<80 20 0.4
80≤x<90 a 0.2
90≤x<100 5 b
18.某供电公司为了解2020年4月份某小区家庭月用电情况,随机调查了该小区部分家庭,并将调查数据进行整理,绘制了如下尚不完整的统计图表.
调查结果统计表:
月用电量x(千瓦时) 频数(户) 频率
0<x≤20 2 0.04
20<x≤40 12
40<x≤60 a 0.36
60<x≤80 8 0.16
80<x≤100 6 b
100<x≤120
0.08
合计 c 1
根据以上信息解答下列问题:
(1)统计表中,a= b= c= ;
(2)请把频数分布直方图补充完整;
(3)求该小区月用电量超过80千瓦时的家庭数占被调查家庭总数的百分比;
(4)若该小区有1000户家庭,根据调查数据估计该小区月用电量不超过60千瓦时的家庭大约有多少户?
19.为了加强学生安全教育,某校举行了一次“安全知识竞赛”初赛,共有1200名学生参加.为了解本次初赛成绩,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计,请你根据下面的频数分布表和频数分布直方图,解答下列问题:
(1)抽取的样本容量是 ;
(2)频数分布表中,a= ,b= ,并请补全频数分布直方图;
(3)如果成绩达到80分以上者为优秀,可推荐参加决赛,请通过计算估计进入决赛的学生人数.
分组 频数 频率
50.5~60.5 4 0.08
60.5~70.5 8 0.16
70.5~80.5 12 0.24
80.5~90.5 15 0.30
90.5~100.5 a b
合计
20.某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成统计图表进行分析.频数分布表
组别 销售数量(件) 频数 频率
A 20≤x<40 3 0.06
B 40≤x<60 7 0.14
C 60≤x<80 12 a
D 80≤x<100 m 0.48
E 100≤x<120 4 0.08
合计 b 1
请根据以上信息,解决下列问题:
(1)频数分布表中,a= 、b= ;
(2)补全频数分布直方图;
(3)如果该季度销量不低于100件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
参考答案
一.选择题
1.解:第4小组的频数:50﹣2﹣8﹣15﹣5=20,
第4小组的频率为:20÷50=0.4.
∴第4小组的频率为0.4.
故选:C.
2.解:A、随着试验次数的增多,某一事件发生的频率不会改变,故原说法错误,符合题意;
B、一个事件A试验中出现的次数越多,频数就越大,正确,不合题意;
C、试验的总次数一定时,频率与频数成正比,正确,不合题意;
D、频数与频率都能反映一个事件出现的频繁程度,正确,不合题意;
故选:A.
3.解:1200×(1﹣)=27,27比较接近24,
故选:B.
4.解:跳绳次数不少于100次的占(10+18+12)÷50×100%=80%,故选项A正确;
多数学生跳绳次数在120﹣140范围内,故选项B错误;
跳绳次数最多的小于160次,故选项C错误;
由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有:800×=64(人),故选项D错误;
故选:A.
5.解:(80﹣56)÷5
=24÷5
=4…4,
故可以把数据分成5组,
故选:B.
6.解:A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率是,不符合题意;
B.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球的概率为,不符合题意;
C.掷一个质地均匀的正六面体骰子,向上的面点数是4的概率为≈0.17,符合题意;
D.掷一枚一元硬币,落地后正面上的概率为,不符合题意;
故选:C.
7.解:∵最大值是17,最小值是6,
∴极差是:17﹣6=11,
∵组距为2,
∴分成的组数是11÷2≈6组;
故选:D.
8.解:根据频数分布表中的数据可知:
第4组的频数为:40﹣12﹣4﹣6﹣10=8,
所以第4组的频率为:8÷40=0.2.
故选:A.
二.填空题
9.解:∵共射击10发,射中8环的频率是0.4,
∴射中8环的频数是:10×0.4=4,
故答案为:4.
10.解:频数为80×0.15=12,
故答案为:12.
11.解:该班学生体育成绩良好的百分率是:×100%=40%.
故答案为:40%.
12.解:∵将一枚硬币随意上抛10次,落地时正面朝上的有6次,
∴反面朝上的频率为:=0.4.
故答案为:0.4.
13.解:∵共有23个数据,
∴射击成绩的中位数是第12个数据,即中位数为9,
故答案为:9.
14.解:2000×=680,
所以估计全校每周课外阅读时间不超过2小时的学生有680人.
故答案为680.
15.解:∵锻炼时间在0﹣2小时的学生的频率是20%,人数为8,
∴被调查的总人数为8÷20%=40(人),
则锻炼时间在4﹣6小时的学生的频率是10÷40=0.25,
故答案为:0.25.
16.解:1000×=400(人),
即该校视力为4.9及以上的学生约有400人,
故答案为:400.
三.解答题
17.解:(1)八甲班的学生有:5÷0.1=50(人),
a=50×0.2=10,b=5÷50=0.1,
即频数分布表中a和b的值分别为10,0.1;
(2)由(1)知,a=10,
补全的频数分布直方图如右图所示;
(3)(1﹣0.1)×100%=0.9×100%=90%,
即该班本次数学考试的及格率是90%.
18.解:(1)c=2÷0.04=50,b=6÷50=0.12,a=50×0.36=18,
故答案为:18,0.12,50;
(2)50×0.08=4,补全频数分布直方图如下:
(3)(6+4)÷50×100%=20%,
答:用电量超过80千瓦时的家庭数占被调查家庭总数的20%;
(4)(户),
答:该小区月用电量不超过60千瓦时的家庭大约有640户.
19.解:(1)4÷0.08=50(人),
故答案为:50;
(2)a=50﹣4﹣8﹣12﹣15=11,b=1﹣0.08﹣0.18﹣0.24﹣0.30=0.22,
故答案为:11,0.22,
补全频数分布直方图如图所示;
(3)1200×(0.30+0.22)=624(人),
答:估计进入决赛的学生人数有624人.
20.解:(1)b=3÷0.06=50,a=12÷50=0.24,
故答案为:0.24,50;
(2)m=50×0.48=24,补全频数分布直方图如下:
(3)400×0.08=32(人),
答:该季度被评为“优秀员工”的人数为32人.
一.选择题
1.在一个样本中,50个数据分别落在5个小组内,第1、2、3、5小组数据的个数分别是2、8、15、5,则第4小组的频率是( )
A.0.6 B.20 C.0.4 D.30
2.下列说法错误的是( )
A.随着试验次数的增多,某一事件发生的频率就会不断增大
B.一个事件A试验中出现的次数越多,频数就越大
C.试验的总次数一定时,频率与频数成正比
D.频数与频率都能反映一个事件出现的频繁程度
3.对一批衬衣进行抽检,得到合格衬衣的频数表如下,若出售1200件衬衣,则其中次品的件数大约是( )
抽取件数(件) 50 100 150 200 500 800 1000
合格频数 48 98 144 193 489 784 981
A.12 B.24 C.1188 D.1176
4.为了了解某校七年级800名学生的跳绳情况(60秒跳绳的次数),随机对该年级50名学生进行了调查,根据收集的数据绘制了如图所示的频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的次数x为:60≤x<80),则以下说法正确的是( )
A.跳绳次数不少于100次的占80%
B.大多数学生跳绳次数在140﹣160范围内
C.跳绳次数最多的是160次
D.由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有84人
5.某公路上的测速仪,在某一时间段内测得30辆汽车的速度(单位:km/h),其最大值和最小值分别是80,56.为了制作频数直方图,以5为组距,这样,可以把数据分成( )
A.4组 B.5组 C.6组 D.10组
6.某小组做“用频率估计概率”的实验时,统计了某一结果出现的频率,绘制了如图的折线统计图,则符合这一结果的实验最有可能的是( )
A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
C.掷一个质地均匀的正六面体骰子,向上的面点数是4
D.掷一枚一元硬币,落地后正面朝上
7.在一组数据中,最大值是17,最小值是6,绘制频数分布表时,如果取组距为2,那么应分成( )组.
A.3 B.4 C.5 D.6
8.将40个数据分成五组,编成组号为①~⑤的五个组,频数分布如表:
组号 ① ② ③ ④ ⑤
频数 12 4 6
10
则第4组的频率是( )
A.0.2 B.0.3 C.8 D.12
二.填空题
9.一次射击训练中,李磊共射击10发,射中8环的频率是0.4,则射中8环的频数是 .
10.将一个有80个数据的样本经统计分成6组,若某一组的频率为0.15,则该组的频数为 .
11.2020年綦江区中招体考已结束,数据显示,与去年相比,体考成绩略有下滑.今年某中学某班学生体育毕业考试的成绩(成绩取整数),制成如图所示的频数分布直方图,若成绩在44.5~47.5分范围内为良好,则该班学生体育成绩良好的百分率是 .
12.将一枚硬币随意上抛10次,落地时正面朝上的有6次,则反面朝上的频率为 .
13.如图是23名射击运动员的一次测试成绩的频数分布折线图,则射击成绩的中位数 .
14.某学校为了解本校2000名学生的课外阅读情况,从全体学生中随机抽取了部分学生进行调查,并将调查结果绘制成如下的统计表,根据表中信息估计全校每周课外阅读时间不超过2小时的学生有 人.
每周课外阅读时间x(小时) 0≤x≤1 1<x≤2 2<x≤3 x>3
人数 7 10 14 19
15.今年3月,上海市开展了在线学习,同时号召同学们在家要坚持体育锻炼,已知某班学生一周内在家锻炼时间的频数分布直方图如图所示.如果锻炼时间在0﹣2小时的学生的频率是20%,那么锻炼时间在4﹣6小时的学生的频率是 .
16.某校有1000名学生,随机抽查200名学生的视力状况,其频数直方图(每一组含前一个边界值,不含后一个边界值)如图所示,则该校视力为4.9及以上的学生约有 人.
三.解答题
17.八甲班进行了一次数学考试,将成绩绘制成了如下不完整的频数分布表和频数直方图:
(1)求频数分布表中a和b的值;
(2)将频数直方图补充完整;
(3)成绩不低于60分为及格,该班本次数学考试的及格率是多少?
成绩 频数(人数) 频率
50≤x<60 5 0.1
60≤x<70 10 0.2
70≤x<80 20 0.4
80≤x<90 a 0.2
90≤x<100 5 b
18.某供电公司为了解2020年4月份某小区家庭月用电情况,随机调查了该小区部分家庭,并将调查数据进行整理,绘制了如下尚不完整的统计图表.
调查结果统计表:
月用电量x(千瓦时) 频数(户) 频率
0<x≤20 2 0.04
20<x≤40 12
40<x≤60 a 0.36
60<x≤80 8 0.16
80<x≤100 6 b
100<x≤120
0.08
合计 c 1
根据以上信息解答下列问题:
(1)统计表中,a= b= c= ;
(2)请把频数分布直方图补充完整;
(3)求该小区月用电量超过80千瓦时的家庭数占被调查家庭总数的百分比;
(4)若该小区有1000户家庭,根据调查数据估计该小区月用电量不超过60千瓦时的家庭大约有多少户?
19.为了加强学生安全教育,某校举行了一次“安全知识竞赛”初赛,共有1200名学生参加.为了解本次初赛成绩,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计,请你根据下面的频数分布表和频数分布直方图,解答下列问题:
(1)抽取的样本容量是 ;
(2)频数分布表中,a= ,b= ,并请补全频数分布直方图;
(3)如果成绩达到80分以上者为优秀,可推荐参加决赛,请通过计算估计进入决赛的学生人数.
分组 频数 频率
50.5~60.5 4 0.08
60.5~70.5 8 0.16
70.5~80.5 12 0.24
80.5~90.5 15 0.30
90.5~100.5 a b
合计
20.某公司共有400名销售人员,为了解该公司销售人员某季度商品销售情况,随机抽取部分销售人员该季度的销售数量,并把所得数据整理后绘制成统计图表进行分析.频数分布表
组别 销售数量(件) 频数 频率
A 20≤x<40 3 0.06
B 40≤x<60 7 0.14
C 60≤x<80 12 a
D 80≤x<100 m 0.48
E 100≤x<120 4 0.08
合计 b 1
请根据以上信息,解决下列问题:
(1)频数分布表中,a= 、b= ;
(2)补全频数分布直方图;
(3)如果该季度销量不低于100件的销售人员将被评为“优秀员工”,试估计该季度被评为“优秀员工”的人数.
参考答案
一.选择题
1.解:第4小组的频数:50﹣2﹣8﹣15﹣5=20,
第4小组的频率为:20÷50=0.4.
∴第4小组的频率为0.4.
故选:C.
2.解:A、随着试验次数的增多,某一事件发生的频率不会改变,故原说法错误,符合题意;
B、一个事件A试验中出现的次数越多,频数就越大,正确,不合题意;
C、试验的总次数一定时,频率与频数成正比,正确,不合题意;
D、频数与频率都能反映一个事件出现的频繁程度,正确,不合题意;
故选:A.
3.解:1200×(1﹣)=27,27比较接近24,
故选:B.
4.解:跳绳次数不少于100次的占(10+18+12)÷50×100%=80%,故选项A正确;
多数学生跳绳次数在120﹣140范围内,故选项B错误;
跳绳次数最多的小于160次,故选项C错误;
由样本可以估计全年级800人中跳绳次数在60﹣80次的大约有:800×=64(人),故选项D错误;
故选:A.
5.解:(80﹣56)÷5
=24÷5
=4…4,
故可以把数据分成5组,
故选:B.
6.解:A.在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”的概率是,不符合题意;
B.暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球的概率为,不符合题意;
C.掷一个质地均匀的正六面体骰子,向上的面点数是4的概率为≈0.17,符合题意;
D.掷一枚一元硬币,落地后正面上的概率为,不符合题意;
故选:C.
7.解:∵最大值是17,最小值是6,
∴极差是:17﹣6=11,
∵组距为2,
∴分成的组数是11÷2≈6组;
故选:D.
8.解:根据频数分布表中的数据可知:
第4组的频数为:40﹣12﹣4﹣6﹣10=8,
所以第4组的频率为:8÷40=0.2.
故选:A.
二.填空题
9.解:∵共射击10发,射中8环的频率是0.4,
∴射中8环的频数是:10×0.4=4,
故答案为:4.
10.解:频数为80×0.15=12,
故答案为:12.
11.解:该班学生体育成绩良好的百分率是:×100%=40%.
故答案为:40%.
12.解:∵将一枚硬币随意上抛10次,落地时正面朝上的有6次,
∴反面朝上的频率为:=0.4.
故答案为:0.4.
13.解:∵共有23个数据,
∴射击成绩的中位数是第12个数据,即中位数为9,
故答案为:9.
14.解:2000×=680,
所以估计全校每周课外阅读时间不超过2小时的学生有680人.
故答案为680.
15.解:∵锻炼时间在0﹣2小时的学生的频率是20%,人数为8,
∴被调查的总人数为8÷20%=40(人),
则锻炼时间在4﹣6小时的学生的频率是10÷40=0.25,
故答案为:0.25.
16.解:1000×=400(人),
即该校视力为4.9及以上的学生约有400人,
故答案为:400.
三.解答题
17.解:(1)八甲班的学生有:5÷0.1=50(人),
a=50×0.2=10,b=5÷50=0.1,
即频数分布表中a和b的值分别为10,0.1;
(2)由(1)知,a=10,
补全的频数分布直方图如右图所示;
(3)(1﹣0.1)×100%=0.9×100%=90%,
即该班本次数学考试的及格率是90%.
18.解:(1)c=2÷0.04=50,b=6÷50=0.12,a=50×0.36=18,
故答案为:18,0.12,50;
(2)50×0.08=4,补全频数分布直方图如下:
(3)(6+4)÷50×100%=20%,
答:用电量超过80千瓦时的家庭数占被调查家庭总数的20%;
(4)(户),
答:该小区月用电量不超过60千瓦时的家庭大约有640户.
19.解:(1)4÷0.08=50(人),
故答案为:50;
(2)a=50﹣4﹣8﹣12﹣15=11,b=1﹣0.08﹣0.18﹣0.24﹣0.30=0.22,
故答案为:11,0.22,
补全频数分布直方图如图所示;
(3)1200×(0.30+0.22)=624(人),
答:估计进入决赛的学生人数有624人.
20.解:(1)b=3÷0.06=50,a=12÷50=0.24,
故答案为:0.24,50;
(2)m=50×0.48=24,补全频数分布直方图如下:
(3)400×0.08=32(人),
答:该季度被评为“优秀员工”的人数为32人.
