福建省南安市侨光一高2020-2021学年高一下学期期中阶段考试数学试题 Word版含答案
文档属性
| 名称 | 福建省南安市侨光一高2020-2021学年高一下学期期中阶段考试数学试题 Word版含答案 |  | |
| 格式 | doc | ||
| 文件大小 | 787.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 08:05:56 | ||
图片预览



文档简介
侨光一高2020-2021学年高一下学期期中阶段考试
数学试卷
一、客观题
(一)单选题(共10小题,50分;每题只有一个正确选项,选对得5分,选错得0分.)
1.复数,则的虚部是( )
A. B. C. D.
2.已知一组数据为20,30,40,50,50,60,70,80,其中平均数、中位数和众数的大小关系是( )
A. 平均数中位数众数 B. 平均数中位数众数
C. 中位数众数平均数 D. 众数中位数平均数
3.已知圆锥的侧面展开图是一个半圆,且圆锥的底面半径为1,则该圆锥的母线长为( )
A. B. C. D.
4.已知一个四棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为( )
A. B. C. D.
5. 已知向量,则向量在向量方向上的投影是( )
A. B. C. D.
6.设,为两条不同的直线,,为两个不同的平面,给出下列命题:
①若,,则; ②若,,则;
③若,,,则;
④若,,则与所成的角和与所成的角相等.
其中正确命题的序号是( )
A.①② B.②④ C.②③ D.①④
7.随机抽取骑行共享单车的市民进行问卷调查,得到样本的频率分布直方图如图所示.再从这些市民中用分层抽样的方法抽取一个样本进行调查,若第二次抽取的样本中年龄段的人数为14,则第二次抽取的样本中年龄段的人数为( )
A. B. C. D.
8. 中,, , , ,则等于( )
A. B. C. D.
9.△ABC中,若且,则△ABC的形状是( )
A.等边三角形 B.等腰三角形 C.等腰直角三角形 D.直角三角形
10.已知四棱锥P﹣ABCD的顶点都在球O的球面上,底面ABCD是矩形,AB=2AD=4,平面PAD⊥底面ABCD,△PAD为等边三角形,则球面O的表面积为( )
A. B. C.64π D.32π
(二)、多选题(共4题20分;每题有两个或以上的答案,全选对得5分,部分选对但不完整得2分,有错选得0分.)
11.已知复数z在复平面上对应的点为Z(3,﹣1),i为虚数单位,则下列正确的是( )
A.z=﹣1+3i B.=10 C.=3+i D.z+i是实数
12.下列关于平面向量的说法中不正确的是( )
A.,,若,则与的夹角为钝角
B.若平面上四个点,,,满足,则,,三点共线.
C. 向量,不能作为平面内所有向量的一组基底
D.若且,则
13.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,其中在卷五“三斜求积”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幕减中斜幂,余半之,自乘于上,以小斜冪乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”即.现有△ABC满足sinA:sinB:sinC=2:3:,且△ABC的面积S△ABC=,请运用上述公式判断下列命题正确的是( )
A.△ABC周长为5+
B.△ABC三个内角A,C,B满足关系A+B=2C
C.△ABC外接圆半径为
D.△ABC中线CD的长为
14.如图,在正方体中,点在线段上运动,则下列正确的是( )
A.直线平面
B.二面角的大小为
C.三棱锥的体积为定值
D.异面直线与所成角的取值范围是
二、填空题(共4小题20分;答对得5分,答错或漏答得0分.)
15.若复数满足:,则______
16.已知30个数据的分位数是,这30个数据从小到大排列后第18个数据是,则第19个数据是______.
17.瑞云塔是福清著名的历史文化古迹. 如图,一研究性小组同学为了估测塔的高度,在塔底D和A,B(与塔底D同一水平面)处进行测量,在点A,B处测得塔顶C的仰角分别为45°,30°,且A,B两点相距,由点D看A,B的张角为150°,则瑞云塔的高度CD=______m
18. 已知向量满足,,则的最大值为______
三、解答题(共5题60分;解答过程应写出文字说明、证明过程或演算步骤.)
19.(12分)已知,,是同一平面内的三个向量,其中=(1,2).
(1)若,且∥,求的坐标.
(2)若,且与垂直,求与的夹角.
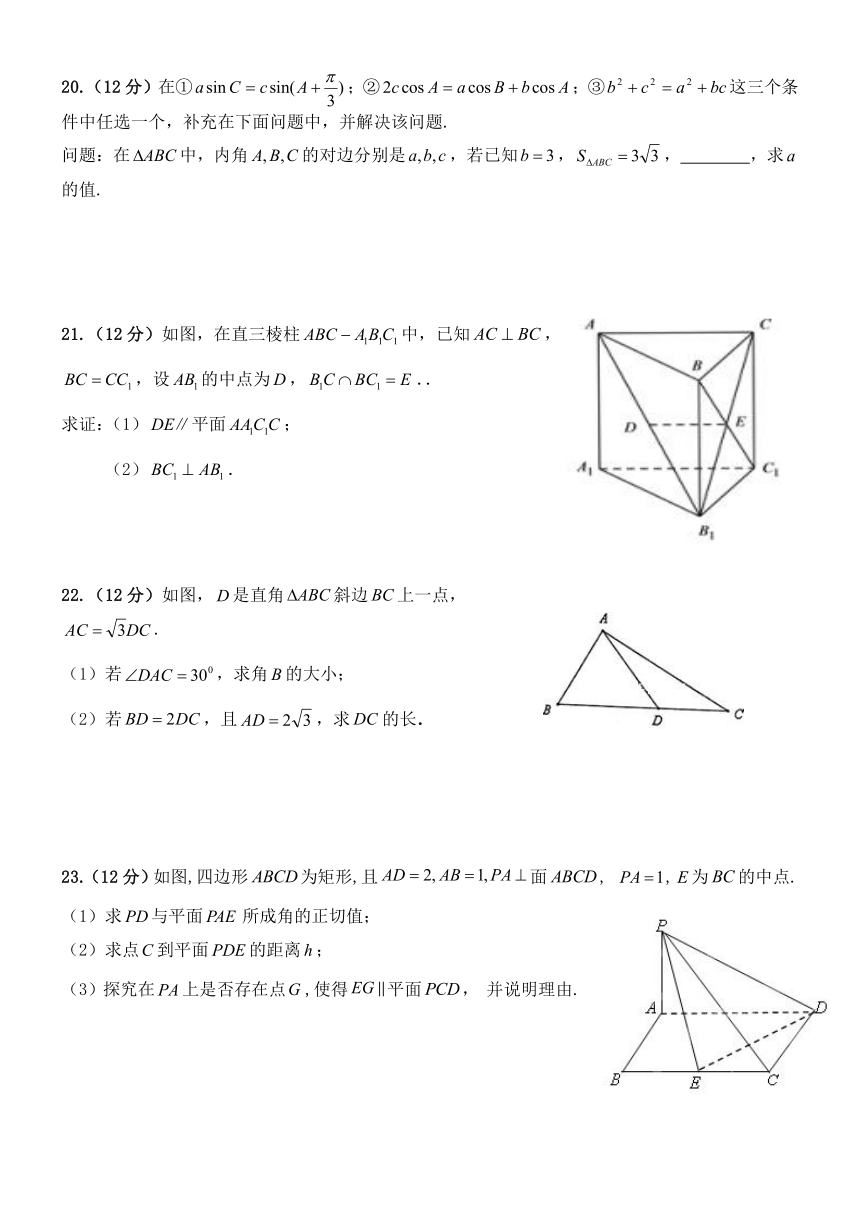
20.(12分)在①;②;③这三个条件中任选一个,补充在下面问题中,并解决该问题.
问题:在中,内角的对边分别是,若已知,, ,求的值.
21.(12分)如图,在直三棱柱中,已知,,设的中点为,..
求证:(1)平面;
(2).
22.(12分)如图,是直角斜边上一点,.
(1)若,求角的大小;
(2)若,且,求的长.
23.(12分)如图,四边形为矩形,且面, ,为的中点.
(1)求与平面所成角的正切值;
(2)求点到平面的距离;
(3)探究在上是否存在点,使得平面, 并说明理由.
2020-2021学年高一下学期期中阶段考试
数学参考答案
一.单选题 1---5: C D C A D 6---10: B A D C B
多选题 11、CD 12、 AD 13、 ABD 14、 AC
二.填空题
三.解答题
19.解:(1)∵;
∴设,且,;
∴;
∴k=±2;
∴,或
(2)∵,且;
∴
=0;
∴;
又;
∴与的夹角为.
20.解:若选①:因为,
所以,
因为,所以
所以,
即
所以,因为,所以.
所以,所以,
所以,所以.
若选②:因为,
所以,
所以
因为,所以,所以,
因为,所以,
所以,所以,
所以,所以
若选③:因为,所以,
所以,
因为,所以,
所以,所以,
所以,所以.
21.(1)在直三棱柱中,
∵平面,且
∴矩形是正方形,∴为的中点,
又为的中点,∴,
又∵平面,平面,
∴平面
(2)在直三棱柱中,
∵平面,平面,∴
又∵,平面,平面,
∴平面,
∵平面,∴
∵矩形是正方形,∴,
∵,平面,,∴平面
又∵平面,∴.
22、解:在中,根据正弦定理,有.
因为,所以
又,所以.
于是,所以.
设,则,,.
于是,,
在中,由余弦定理,得 ,
即,得,故 .
23.(1)连结,∵为的中点,,
∴为等腰直角三角形,
则,同理可得,∴,∴,
又,且, ∴,
又∵,∴,
∴与平面所成角即为
又由已知可求得,
∴在中,
(2)由(1)知为腰长为1的等腰直角三角形,的直角边为,
∴,
而是三棱锥的高,
∴.
∴点到平面的距离
(3)在上存在中点,使得.理由如下:
取的中点,连结.
∵是的中点, ∴,且,
又因为E为BC的中点,且四边形ABCD为矩形,所以EC//AD,且EC=AD,
所以EC//GH,且EC=GH,所以四边形EGHC是平行四边形,所以EG//CH,
又EG平面PCD,CH平面PCD,所以EG//平面PCD.
数学试卷
一、客观题
(一)单选题(共10小题,50分;每题只有一个正确选项,选对得5分,选错得0分.)
1.复数,则的虚部是( )
A. B. C. D.
2.已知一组数据为20,30,40,50,50,60,70,80,其中平均数、中位数和众数的大小关系是( )
A. 平均数中位数众数 B. 平均数中位数众数
C. 中位数众数平均数 D. 众数中位数平均数
3.已知圆锥的侧面展开图是一个半圆,且圆锥的底面半径为1,则该圆锥的母线长为( )
A. B. C. D.
4.已知一个四棱锥的高为3,其底面用斜二测画法所画出的水平放置的直观图是一个边长为1的正方形,则此四棱锥的体积为( )
A. B. C. D.
5. 已知向量,则向量在向量方向上的投影是( )
A. B. C. D.
6.设,为两条不同的直线,,为两个不同的平面,给出下列命题:
①若,,则; ②若,,则;
③若,,,则;
④若,,则与所成的角和与所成的角相等.
其中正确命题的序号是( )
A.①② B.②④ C.②③ D.①④
7.随机抽取骑行共享单车的市民进行问卷调查,得到样本的频率分布直方图如图所示.再从这些市民中用分层抽样的方法抽取一个样本进行调查,若第二次抽取的样本中年龄段的人数为14,则第二次抽取的样本中年龄段的人数为( )
A. B. C. D.
8. 中,, , , ,则等于( )
A. B. C. D.
9.△ABC中,若且,则△ABC的形状是( )
A.等边三角形 B.等腰三角形 C.等腰直角三角形 D.直角三角形
10.已知四棱锥P﹣ABCD的顶点都在球O的球面上,底面ABCD是矩形,AB=2AD=4,平面PAD⊥底面ABCD,△PAD为等边三角形,则球面O的表面积为( )
A. B. C.64π D.32π
(二)、多选题(共4题20分;每题有两个或以上的答案,全选对得5分,部分选对但不完整得2分,有错选得0分.)
11.已知复数z在复平面上对应的点为Z(3,﹣1),i为虚数单位,则下列正确的是( )
A.z=﹣1+3i B.=10 C.=3+i D.z+i是实数
12.下列关于平面向量的说法中不正确的是( )
A.,,若,则与的夹角为钝角
B.若平面上四个点,,,满足,则,,三点共线.
C. 向量,不能作为平面内所有向量的一组基底
D.若且,则
13.《数书九章》是中国南宋时期杰出数学家秦九韶的著作,全书十八卷共八十一个问题,分为九类,每类九个问题,其中在卷五“三斜求积”中提出了已知三角形三边a,b,c求面积的公式,这与古希腊的海伦公式完全等价,其求法是:“以小斜幂并大斜幕减中斜幂,余半之,自乘于上,以小斜冪乘大斜幂减上,余四约之,为实,一为从隅,开平方得积.”即.现有△ABC满足sinA:sinB:sinC=2:3:,且△ABC的面积S△ABC=,请运用上述公式判断下列命题正确的是( )
A.△ABC周长为5+
B.△ABC三个内角A,C,B满足关系A+B=2C
C.△ABC外接圆半径为
D.△ABC中线CD的长为
14.如图,在正方体中,点在线段上运动,则下列正确的是( )
A.直线平面
B.二面角的大小为
C.三棱锥的体积为定值
D.异面直线与所成角的取值范围是
二、填空题(共4小题20分;答对得5分,答错或漏答得0分.)
15.若复数满足:,则______
16.已知30个数据的分位数是,这30个数据从小到大排列后第18个数据是,则第19个数据是______.
17.瑞云塔是福清著名的历史文化古迹. 如图,一研究性小组同学为了估测塔的高度,在塔底D和A,B(与塔底D同一水平面)处进行测量,在点A,B处测得塔顶C的仰角分别为45°,30°,且A,B两点相距,由点D看A,B的张角为150°,则瑞云塔的高度CD=______m
18. 已知向量满足,,则的最大值为______
三、解答题(共5题60分;解答过程应写出文字说明、证明过程或演算步骤.)
19.(12分)已知,,是同一平面内的三个向量,其中=(1,2).
(1)若,且∥,求的坐标.
(2)若,且与垂直,求与的夹角.
20.(12分)在①;②;③这三个条件中任选一个,补充在下面问题中,并解决该问题.
问题:在中,内角的对边分别是,若已知,, ,求的值.
21.(12分)如图,在直三棱柱中,已知,,设的中点为,..
求证:(1)平面;
(2).
22.(12分)如图,是直角斜边上一点,.
(1)若,求角的大小;
(2)若,且,求的长.
23.(12分)如图,四边形为矩形,且面, ,为的中点.
(1)求与平面所成角的正切值;
(2)求点到平面的距离;
(3)探究在上是否存在点,使得平面, 并说明理由.
2020-2021学年高一下学期期中阶段考试
数学参考答案
一.单选题 1---5: C D C A D 6---10: B A D C B
多选题 11、CD 12、 AD 13、 ABD 14、 AC
二.填空题
三.解答题
19.解:(1)∵;
∴设,且,;
∴;
∴k=±2;
∴,或
(2)∵,且;
∴
=0;
∴;
又;
∴与的夹角为.
20.解:若选①:因为,
所以,
因为,所以
所以,
即
所以,因为,所以.
所以,所以,
所以,所以.
若选②:因为,
所以,
所以
因为,所以,所以,
因为,所以,
所以,所以,
所以,所以
若选③:因为,所以,
所以,
因为,所以,
所以,所以,
所以,所以.
21.(1)在直三棱柱中,
∵平面,且
∴矩形是正方形,∴为的中点,
又为的中点,∴,
又∵平面,平面,
∴平面
(2)在直三棱柱中,
∵平面,平面,∴
又∵,平面,平面,
∴平面,
∵平面,∴
∵矩形是正方形,∴,
∵,平面,,∴平面
又∵平面,∴.
22、解:在中,根据正弦定理,有.
因为,所以
又,所以.
于是,所以.
设,则,,.
于是,,
在中,由余弦定理,得 ,
即,得,故 .
23.(1)连结,∵为的中点,,
∴为等腰直角三角形,
则,同理可得,∴,∴,
又,且, ∴,
又∵,∴,
∴与平面所成角即为
又由已知可求得,
∴在中,
(2)由(1)知为腰长为1的等腰直角三角形,的直角边为,
∴,
而是三棱锥的高,
∴.
∴点到平面的距离
(3)在上存在中点,使得.理由如下:
取的中点,连结.
∵是的中点, ∴,且,
又因为E为BC的中点,且四边形ABCD为矩形,所以EC//AD,且EC=AD,
所以EC//GH,且EC=GH,所以四边形EGHC是平行四边形,所以EG//CH,
又EG平面PCD,CH平面PCD,所以EG//平面PCD.
同课章节目录
