四年级下册数学教案-第4单元整理复习 人教版
文档属性
| 名称 | 四年级下册数学教案-第4单元整理复习 人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 363.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 11:10:43 | ||
图片预览



文档简介
小数的意义和性质整理和复习
教学目标:
1.梳理本单元知识点,让学生进一步理解和掌握小数的意义、性质、小数点的位置移动规律以及求近似数等知识。
2.通过不同形式的练习,分层次检验学生知识掌握情况,在练习中及时查漏补缺。
3.在解题过程中培养学生读题能力,提高学生解决问题的能力。
教学过程:
一、复习回顾
同学们,第四单元我们都学习了哪些知识呢?请你结合下面的提纲,回忆一下吧?
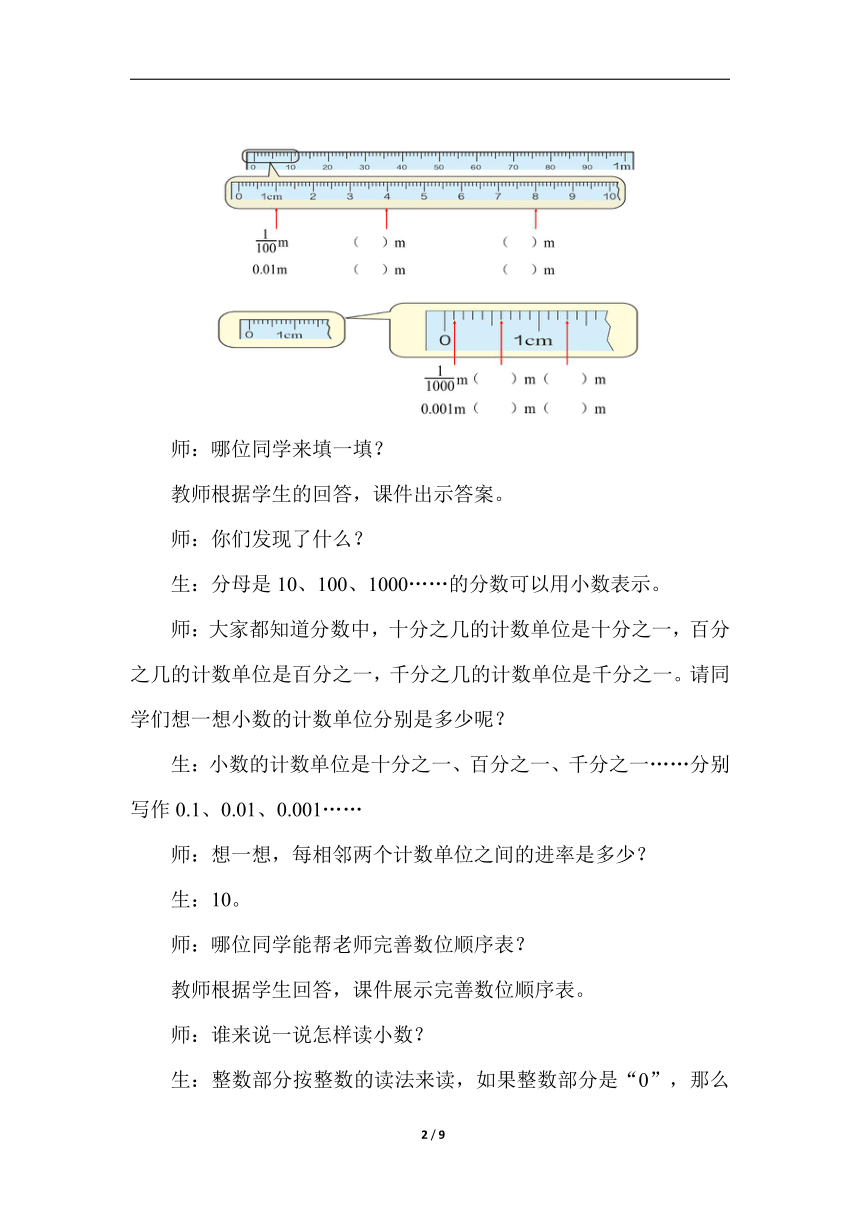
1.小数的意义和读写法
课件展示:
师:哪位同学来填一填?
教师根据学生的回答,课件出示答案。
师:你们发现了什么?
生:分母是10、100、1000……的分数可以用小数表示。
师:大家都知道分数中,十分之几的计数单位是十分之一,百分之几的计数单位是百分之一,千分之几的计数单位是千分之一。请同学们想一想小数的计数单位分别是多少呢?
生:小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001……
师:想一想,每相邻两个计数单位之间的进率是多少?
生:10。
师:哪位同学能帮老师完善数位顺序表?
教师根据学生回答,课件展示完善数位顺序表。
师:谁来说一说怎样读小数?
生:整数部分按整数的读法来读,如果整数部分是“0”,那么整数部分读作“零”;小数点读作“点”;小数部分要依次读出每个数字,小数部分有几个“0”就读出几个“零”。
师:又怎样写小数呢?
生:整数部分按照整数写法来写,如果是“零”写作“0”;小数点写在个位右下角,要写成小圆点“.”,不要写成顿号;小数部分按照读法顺序依次写出每个数字,不能遗漏。
2.小数的性质和大小比较
师:小数有怎样的性质?谁来说一说?
生:小数的末尾添上“0”或去掉“0”,小数的大小不变。这就是小数的性质。
师:应用小数的性质可以根据需要对小数进行化简和改写,谁来给大家讲一讲?
生1:去掉小数末尾的“0”,就可以把小数写成简单的形式,这个过程叫做化简。
师:在应用小数的性质改写小数时要注意什么?
生2:只能在小数的末尾添上“0”或去掉“0”,其他数位上的“0”不能动。
生3:把一个整数改写成指定小数位数的小数时,不要忘记在个位的右下角点上小数点。
师:怎样比较两个小数的大小?
生:先看它们的整数部分,整数部分大的那个数就大;当整数部分相同时,十分位上的数大的那个数就大;十分位上的数也相同时,百分位上的数大的那个数就大……
3.小数点的移动引起的小数大小的变化
师:小数点位置的移动引起了小数大小的什么变化?变化规律是什么?
生1:小数点向右
移动一位,相当于把原数乘10,小数就扩大到原数的10倍;
移动两位,相当于把原数乘100,小数就扩大到原数的100倍;
移动三位,相当于把原数乘1000,小数就扩大到原数的1000倍;
……
生2:小数点向左
移动一位,相当于把原数除以10,小数就缩小到原数的;
移动两位,相当于把原数除以100,小数就缩小到原数的;
移动三位,相当于把原数除以1000,小数就缩小到原数的;
……
师:你们知道怎样应用这个规律吗?
生1:把一个小数扩大到原来的10倍、100倍、1000倍……就是把这个小数分别乘10、100、1000……,也就是把小数点分别向右移动一位、两位、三位……
生2:把一个小数缩小到原来的、、……,就是把这个小数分别除以10、100、1000……,也就是把小数点分别向左移动一位、两位、三位……
师:在利用小数点移动的规律解决实际问题时,得到答案后要注意检验,可以从问题出发去检验。另外,在乘法(或除法)中,如果因数(或除数)是10、100、1000……就可以直接利用小数点移动的规律来计算。
4.小数与单位的换算
师:把低级单位的数改写成高级单位的数,该怎样做?
生:把低级单位的数改写成高级单位的数,我们可以用低级单位的数除以它们之间的进率,如果进率是10、100、1000……,只要把小数点向左移动一位、两位、三位……
师:把复名数改写成用小数表示的高级单位的单名数时,应该怎么办?
生:复名数中高级单位的数不动,作为小数的整数部分;再把复名数中低级单位的数改写成高级单位的数,作为小数部分。
师:把高级单位的数改写成低级单位的数,该怎样做?
生:将高级单位的数改写成低级单位的数,要乘单位间的进率,如果进率是10、100、1000……,只要把小数点向右移动一位、两位、三位……
师:把用小数表示的高级单位的单名数改写成含有低级单位的复名数时,应该怎么办?
生:小数的整数部分直接作为高级单位的数,小数的小数部分乘进率或通过小数点的移动转化成低级单位的数。
5.小数的近似数
师:想一想求小数的近似数的方法是什么?
生1:求小数的近似数时,可以用“四舍五入”法。
当保留整数时,表示精确到个位,应根据十分位上数的大小判断是否进位;保留一位小数时,表示精确到十分位,应根据百分位上数的大小判断是否进位;保留两位小数时,表示精确到百分位,应根据千分位上数的大小判断是否进位……
生2:在表示近似数时,小数末尾的0不能去掉。
师:如何把不是整万或整亿的数改写成用“万”或“亿”作单位的数?
师生交流后明确:改写时,只要在“万”或“亿”位的右边点,上小数点,去掉小数末尾的“0”,在数的后面加上“万”或“亿”字。
教师出示课件。
师:大家总结的非常棒,大家记清楚小数的意义、性质、小数点的位置移动规律以及求近似数等知识,在练习中就会减少出错。
设计意图:通过教师提问引起学生回忆,师生一起总结学过的知识,建立完整的知识体系。
二、基础练习
1.0.586是由(
)个0.1、(
)个0.01和(
)个0.001组成的。
2.黄果树瀑布高约七十七点八m。横线上的数写作(
);世界上最小的蜘蛛是展蜘蛛,它只有0.043cm长。横线上的数读作(
)。
3.判断:在小数点的后面添上或去掉0,小数的大小不变。(
)
4.在下列各数中,去掉“0”而大小不变的小数是(
)。
A.5.830
B.0.006
C.7.08
D.600
5.把9先缩小到它的,再扩大到新数的100倍,结果是原来的(
)。
A.100倍
B.1000倍
C.10倍
D.
6.在里填上“>”“<”或“=”。
0.750.705
0.0680.68
6.9156.92
0.57m57cm
9千克50克9.5千克
7.85cm=(
)m
2064g=(
)kg
2.3dm=(
)cm
0.48m(
)dm
1.6t=(
)kg
6.012km=(
)m
62mm=(
)m
200kg=(
)t
8.把499630000改写成用“亿”作单位的数并精确到百分位是(
)。
A.4.99亿
B.5.0亿
C.5.00亿
D.49.96亿
设计意图:在基础练习中进一步复习本单元基础知识,让学生对小数的意义、性质、小数点的位置移动规律以及求近似数等知识有更深的理解。
三、易错练习
1.把215的小数点向左移动一位是(
);把(
)扩大到原来的100倍是6;把(
)缩小到原来的是0.82。
2.下面各数中,要读出两个“零”的数是(
)。
A.2.10008
B.210.008
C.2100.08
D.201.008
3.按要求取近似数。
保留两位小数
保留一位小数
保留整数
0.8738
2.5954
9.985
4.按要求改写表格中的数。
改写成用“万”作单位的数
改写成用“亿”作单位的数
27000000
40050000
508090000
5.某日人民币与外币的兑换价如下。
设计意图:通过不同形式的考查,进一步巩固学生对本单元知识的理解和掌握。
四、拓展练习
1.按要求在里填数。
(1)里最小能填几?
0.5
m>25cm
1g>0.017kg
12.3km2>1252公顷
(2)里最大能填几?
0.5m<35cm
1g<0.019kg
1.6m2<170dm2
2.用数字5、2、4、0和小数点按要求写出下面各小数(每个数字只能用一次,每题写出一个)。
(1)大于5且小数部分是三位的小数。
(2)小于1且小数部分是三位的小数。
(3)0不读出来且小数部分是两位的小数。
3.甲、乙两数的和是814,把甲数的小数点向左移动一位后与乙数相等,甲、乙两数分别是多少?
设计意图:通过变式,培养学生初步的推理习惯,提高学生解决问题的能力
2
/
2
教学目标:
1.梳理本单元知识点,让学生进一步理解和掌握小数的意义、性质、小数点的位置移动规律以及求近似数等知识。
2.通过不同形式的练习,分层次检验学生知识掌握情况,在练习中及时查漏补缺。
3.在解题过程中培养学生读题能力,提高学生解决问题的能力。
教学过程:
一、复习回顾
同学们,第四单元我们都学习了哪些知识呢?请你结合下面的提纲,回忆一下吧?
1.小数的意义和读写法
课件展示:
师:哪位同学来填一填?
教师根据学生的回答,课件出示答案。
师:你们发现了什么?
生:分母是10、100、1000……的分数可以用小数表示。
师:大家都知道分数中,十分之几的计数单位是十分之一,百分之几的计数单位是百分之一,千分之几的计数单位是千分之一。请同学们想一想小数的计数单位分别是多少呢?
生:小数的计数单位是十分之一、百分之一、千分之一……分别写作0.1、0.01、0.001……
师:想一想,每相邻两个计数单位之间的进率是多少?
生:10。
师:哪位同学能帮老师完善数位顺序表?
教师根据学生回答,课件展示完善数位顺序表。
师:谁来说一说怎样读小数?
生:整数部分按整数的读法来读,如果整数部分是“0”,那么整数部分读作“零”;小数点读作“点”;小数部分要依次读出每个数字,小数部分有几个“0”就读出几个“零”。
师:又怎样写小数呢?
生:整数部分按照整数写法来写,如果是“零”写作“0”;小数点写在个位右下角,要写成小圆点“.”,不要写成顿号;小数部分按照读法顺序依次写出每个数字,不能遗漏。
2.小数的性质和大小比较
师:小数有怎样的性质?谁来说一说?
生:小数的末尾添上“0”或去掉“0”,小数的大小不变。这就是小数的性质。
师:应用小数的性质可以根据需要对小数进行化简和改写,谁来给大家讲一讲?
生1:去掉小数末尾的“0”,就可以把小数写成简单的形式,这个过程叫做化简。
师:在应用小数的性质改写小数时要注意什么?
生2:只能在小数的末尾添上“0”或去掉“0”,其他数位上的“0”不能动。
生3:把一个整数改写成指定小数位数的小数时,不要忘记在个位的右下角点上小数点。
师:怎样比较两个小数的大小?
生:先看它们的整数部分,整数部分大的那个数就大;当整数部分相同时,十分位上的数大的那个数就大;十分位上的数也相同时,百分位上的数大的那个数就大……
3.小数点的移动引起的小数大小的变化
师:小数点位置的移动引起了小数大小的什么变化?变化规律是什么?
生1:小数点向右
移动一位,相当于把原数乘10,小数就扩大到原数的10倍;
移动两位,相当于把原数乘100,小数就扩大到原数的100倍;
移动三位,相当于把原数乘1000,小数就扩大到原数的1000倍;
……
生2:小数点向左
移动一位,相当于把原数除以10,小数就缩小到原数的;
移动两位,相当于把原数除以100,小数就缩小到原数的;
移动三位,相当于把原数除以1000,小数就缩小到原数的;
……
师:你们知道怎样应用这个规律吗?
生1:把一个小数扩大到原来的10倍、100倍、1000倍……就是把这个小数分别乘10、100、1000……,也就是把小数点分别向右移动一位、两位、三位……
生2:把一个小数缩小到原来的、、……,就是把这个小数分别除以10、100、1000……,也就是把小数点分别向左移动一位、两位、三位……
师:在利用小数点移动的规律解决实际问题时,得到答案后要注意检验,可以从问题出发去检验。另外,在乘法(或除法)中,如果因数(或除数)是10、100、1000……就可以直接利用小数点移动的规律来计算。
4.小数与单位的换算
师:把低级单位的数改写成高级单位的数,该怎样做?
生:把低级单位的数改写成高级单位的数,我们可以用低级单位的数除以它们之间的进率,如果进率是10、100、1000……,只要把小数点向左移动一位、两位、三位……
师:把复名数改写成用小数表示的高级单位的单名数时,应该怎么办?
生:复名数中高级单位的数不动,作为小数的整数部分;再把复名数中低级单位的数改写成高级单位的数,作为小数部分。
师:把高级单位的数改写成低级单位的数,该怎样做?
生:将高级单位的数改写成低级单位的数,要乘单位间的进率,如果进率是10、100、1000……,只要把小数点向右移动一位、两位、三位……
师:把用小数表示的高级单位的单名数改写成含有低级单位的复名数时,应该怎么办?
生:小数的整数部分直接作为高级单位的数,小数的小数部分乘进率或通过小数点的移动转化成低级单位的数。
5.小数的近似数
师:想一想求小数的近似数的方法是什么?
生1:求小数的近似数时,可以用“四舍五入”法。
当保留整数时,表示精确到个位,应根据十分位上数的大小判断是否进位;保留一位小数时,表示精确到十分位,应根据百分位上数的大小判断是否进位;保留两位小数时,表示精确到百分位,应根据千分位上数的大小判断是否进位……
生2:在表示近似数时,小数末尾的0不能去掉。
师:如何把不是整万或整亿的数改写成用“万”或“亿”作单位的数?
师生交流后明确:改写时,只要在“万”或“亿”位的右边点,上小数点,去掉小数末尾的“0”,在数的后面加上“万”或“亿”字。
教师出示课件。
师:大家总结的非常棒,大家记清楚小数的意义、性质、小数点的位置移动规律以及求近似数等知识,在练习中就会减少出错。
设计意图:通过教师提问引起学生回忆,师生一起总结学过的知识,建立完整的知识体系。
二、基础练习
1.0.586是由(
)个0.1、(
)个0.01和(
)个0.001组成的。
2.黄果树瀑布高约七十七点八m。横线上的数写作(
);世界上最小的蜘蛛是展蜘蛛,它只有0.043cm长。横线上的数读作(
)。
3.判断:在小数点的后面添上或去掉0,小数的大小不变。(
)
4.在下列各数中,去掉“0”而大小不变的小数是(
)。
A.5.830
B.0.006
C.7.08
D.600
5.把9先缩小到它的,再扩大到新数的100倍,结果是原来的(
)。
A.100倍
B.1000倍
C.10倍
D.
6.在里填上“>”“<”或“=”。
0.750.705
0.0680.68
6.9156.92
0.57m57cm
9千克50克9.5千克
7.85cm=(
)m
2064g=(
)kg
2.3dm=(
)cm
0.48m(
)dm
1.6t=(
)kg
6.012km=(
)m
62mm=(
)m
200kg=(
)t
8.把499630000改写成用“亿”作单位的数并精确到百分位是(
)。
A.4.99亿
B.5.0亿
C.5.00亿
D.49.96亿
设计意图:在基础练习中进一步复习本单元基础知识,让学生对小数的意义、性质、小数点的位置移动规律以及求近似数等知识有更深的理解。
三、易错练习
1.把215的小数点向左移动一位是(
);把(
)扩大到原来的100倍是6;把(
)缩小到原来的是0.82。
2.下面各数中,要读出两个“零”的数是(
)。
A.2.10008
B.210.008
C.2100.08
D.201.008
3.按要求取近似数。
保留两位小数
保留一位小数
保留整数
0.8738
2.5954
9.985
4.按要求改写表格中的数。
改写成用“万”作单位的数
改写成用“亿”作单位的数
27000000
40050000
508090000
5.某日人民币与外币的兑换价如下。
设计意图:通过不同形式的考查,进一步巩固学生对本单元知识的理解和掌握。
四、拓展练习
1.按要求在里填数。
(1)里最小能填几?
0.5
m>25cm
1g>0.017kg
12.3km2>1252公顷
(2)里最大能填几?
0.5m<35cm
1g<0.019kg
1.6m2<170dm2
2.用数字5、2、4、0和小数点按要求写出下面各小数(每个数字只能用一次,每题写出一个)。
(1)大于5且小数部分是三位的小数。
(2)小于1且小数部分是三位的小数。
(3)0不读出来且小数部分是两位的小数。
3.甲、乙两数的和是814,把甲数的小数点向左移动一位后与乙数相等,甲、乙两数分别是多少?
设计意图:通过变式,培养学生初步的推理习惯,提高学生解决问题的能力
2
/
2
