数学人教A版(2019)选择性必修第三册6.2.1排列(共21张PPT)
文档属性
| 名称 | 数学人教A版(2019)选择性必修第三册6.2.1排列(共21张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 435.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 12:01:09 | ||
图片预览






文档简介
(共21张PPT)
第1课时 排列与排列数公式
6.2.1 排 列
若完成一件事情可以有n类方案,在第一类方案中有m1种不同的方法,在第二类中有m2种不同的方法,…在第n类方案中有mn种不同的方法,那么完成这件事情有:
N=m1+m2+m3+m4+……+mn
种不同的方法
若完成一件事情需要n个步骤,在第一步中有m1种不同的方法,在第二步中有m2种不同的方法,…在第n步方法中有mn种不同的方法,那么完成这件事情有:
N=m1×m2×m3×m4×……
×mn
种不同的方法
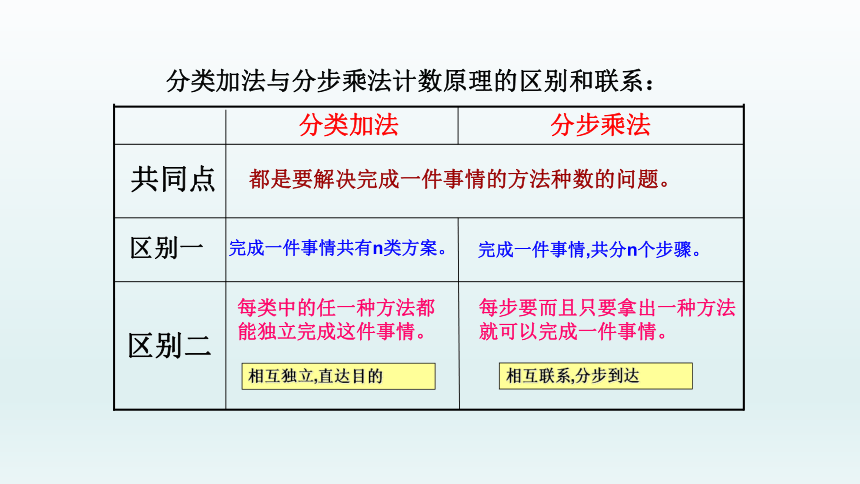
分类加法计数原理
分步乘法计数原理
课前回顾
分步乘法
分类加法
共同点
区别一
完成一件事情共有n类方案。
完成一件事情,共分n个步骤。
区别二
每类中的任一种方法都
能独立完成这件事情。
每步要而且只要拿出一种方法
就可以完成一件事情。
都是要解决完成一件事情的方法种数的问题。
分类加法与分步乘法计数原理的区别和联系:
相互独立,直达目的
相互联系,分步到达
创境设问
探究:
在1.1节的例9中我们看到,用分步乘法计数原理
解决这个问题时,因做了一些重复性工作而显得繁琐。能否对这一类计数问题给出一种简捷的方法呢?
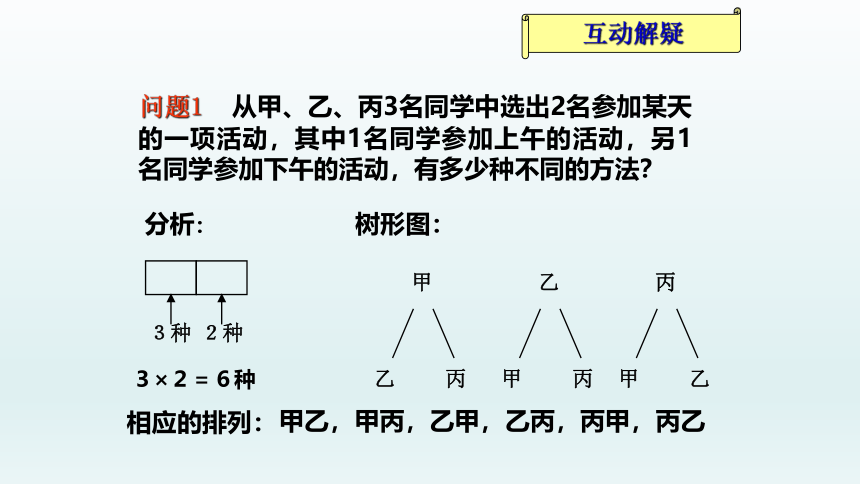
问题1
从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的方法?
互动解疑
3种
2种
3×2=6种
甲
乙
丙
乙
甲
丙
丙
甲
乙
分析:
树形图:
相应的排列:
甲乙,甲丙,乙甲,乙丙,丙甲,丙乙
4种
3种
4×
3×2=24种
2种
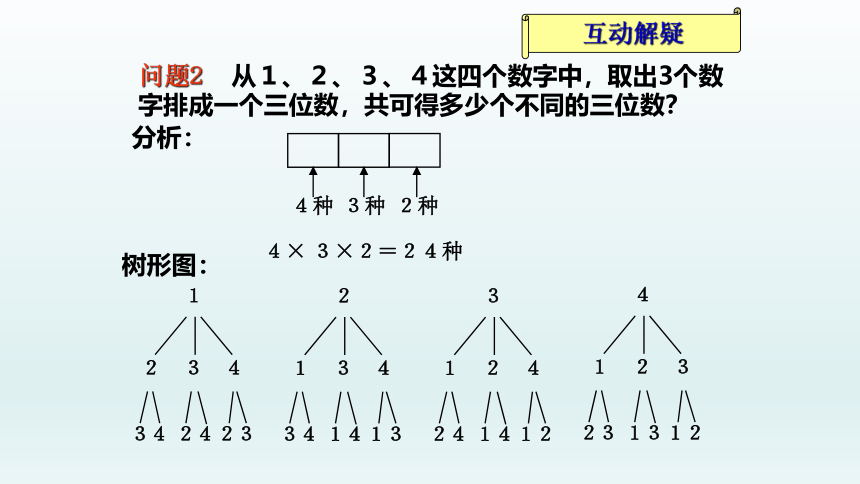
问题2
从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数?
分析:
1
2
3
4
3
4
2
4
2
3
2
1
3
4
3
4
1
4
1
3
3
1
2
4
2
4
1
4
1
2
4
1
2
3
2
3
1
3
1
2
树形图:
互动解疑
从3个不同的元素a,b,c中任取2个,按照一定的顺序排成一列,共有多少种不同的排列方法。
问题1改述为:
互动解疑
问题2改述为:
从4个不同的元素a,b,c,d中任取3个,按照一定的顺序排成一列,共有多少种不同的排列方法。
【
排列】
一般地说,从
n
个不同元素中,任取
m
(m≤n)
个元素,按照一定的顺序排成一列,叫做从
n
个不同元素中取出
m
个元素的一个排列.
排列的特征:
(1)排列包括两个方面:
(2)两个排列相同的充要条件:
元素相同,且排列顺序相同
取出元素→按一定顺序排列
互动解疑
当m=n时,叫做n个元素的一个全排列.
例1
判断下列“事情”是否为排列:
是
是
是
否
(2)从全班40名同学中挑选4人;
(4)从某10人中选取4人参加4×100m接力赛;
(3)将3本不同的书分发给3个人.
(1)5人站成一排照相;
内化迁移
练习
下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3,4四个数字中,任选两个做除法,其不同结果有多少种?
(3)某班有20位同学参加同学聚会,见面时都一一握手,他们共握手多少次?
(4)某班有20位同学参加同学聚会,见面后都互发短信留下自己的电话,他们共发出短信多少条?
内化迁移
【排列数】
从
n
个不同元素中,任取
m
(m≤n)
个元素的所有不同排列的个数,叫做从
n
个不同元素中取出
m
个元素的排列数.
排列与排列数的区别:
排
列:是有序的元素列,不是数
排列数:排列的个数,是数
A
m
n
互动解疑
记作:
问题2中:
问题1中:
思考:你能否得出
的意义和
的值?
排列数为
3×2=6
种
排列数为
4×3×2=24
种
互动解疑
A
2
n
A
2
n
问题3
从n个不同元素中取出2个元素,排成一列,共有多少种排列方法?
问题4
从n个不同元素中取出3个元素,排成一列,共有多少种排列方法?
n种
(n-1)种
n种
(n-1)种
(n-2)种
互动解疑
=n
(n-1)
A
2
n
=n
(n-1)
(n-2)
A
3
n
问题5
从n个不同元素中取出m个元素,排成一列,共有多少种排列方法?
n种
(n-1)种
(n-2)种
(n-m+1)种
…
…
互动解疑
排列数公式:
公式的特征:右边第一个因数是n
,后面每个因数比前一个少1,最后一个因数是n-m+1,共有m个因数
n种
(n-1)种
(n-2)种
(n-m+1)种
…
…
互动解疑
A
n
n
(n的阶乘)
规定:
排列数公式:
排列数:
内化迁移
例3
(1)从5本不同的书中选3本送给3名同学,每人各1本,共有多少种不同的送法?
(种)
(种)
(2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法?
内化迁移
【排列】
关键点:先取后排
【排列数】所有不同排列的个数
【排列数公式】
课堂小结
课堂检测
课后作业
谢谢!
第1课时 排列与排列数公式
6.2.1 排 列
若完成一件事情可以有n类方案,在第一类方案中有m1种不同的方法,在第二类中有m2种不同的方法,…在第n类方案中有mn种不同的方法,那么完成这件事情有:
N=m1+m2+m3+m4+……+mn
种不同的方法
若完成一件事情需要n个步骤,在第一步中有m1种不同的方法,在第二步中有m2种不同的方法,…在第n步方法中有mn种不同的方法,那么完成这件事情有:
N=m1×m2×m3×m4×……
×mn
种不同的方法
分类加法计数原理
分步乘法计数原理
课前回顾
分步乘法
分类加法
共同点
区别一
完成一件事情共有n类方案。
完成一件事情,共分n个步骤。
区别二
每类中的任一种方法都
能独立完成这件事情。
每步要而且只要拿出一种方法
就可以完成一件事情。
都是要解决完成一件事情的方法种数的问题。
分类加法与分步乘法计数原理的区别和联系:
相互独立,直达目的
相互联系,分步到达
创境设问
探究:
在1.1节的例9中我们看到,用分步乘法计数原理
解决这个问题时,因做了一些重复性工作而显得繁琐。能否对这一类计数问题给出一种简捷的方法呢?
问题1
从甲、乙、丙3名同学中选出2名参加某天的一项活动,其中1名同学参加上午的活动,另1名同学参加下午的活动,有多少种不同的方法?
互动解疑
3种
2种
3×2=6种
甲
乙
丙
乙
甲
丙
丙
甲
乙
分析:
树形图:
相应的排列:
甲乙,甲丙,乙甲,乙丙,丙甲,丙乙
4种
3种
4×
3×2=24种
2种
问题2
从1、2、3、4这四个数字中,取出3个数字排成一个三位数,共可得多少个不同的三位数?
分析:
1
2
3
4
3
4
2
4
2
3
2
1
3
4
3
4
1
4
1
3
3
1
2
4
2
4
1
4
1
2
4
1
2
3
2
3
1
3
1
2
树形图:
互动解疑
从3个不同的元素a,b,c中任取2个,按照一定的顺序排成一列,共有多少种不同的排列方法。
问题1改述为:
互动解疑
问题2改述为:
从4个不同的元素a,b,c,d中任取3个,按照一定的顺序排成一列,共有多少种不同的排列方法。
【
排列】
一般地说,从
n
个不同元素中,任取
m
(m≤n)
个元素,按照一定的顺序排成一列,叫做从
n
个不同元素中取出
m
个元素的一个排列.
排列的特征:
(1)排列包括两个方面:
(2)两个排列相同的充要条件:
元素相同,且排列顺序相同
取出元素→按一定顺序排列
互动解疑
当m=n时,叫做n个元素的一个全排列.
例1
判断下列“事情”是否为排列:
是
是
是
否
(2)从全班40名同学中挑选4人;
(4)从某10人中选取4人参加4×100m接力赛;
(3)将3本不同的书分发给3个人.
(1)5人站成一排照相;
内化迁移
练习
下列问题是排列问题吗?
(1)从1,2,3,4四个数字中,任选两个做加法,其不同结果有多少种?
(2)从1,2,3,4四个数字中,任选两个做除法,其不同结果有多少种?
(3)某班有20位同学参加同学聚会,见面时都一一握手,他们共握手多少次?
(4)某班有20位同学参加同学聚会,见面后都互发短信留下自己的电话,他们共发出短信多少条?
内化迁移
【排列数】
从
n
个不同元素中,任取
m
(m≤n)
个元素的所有不同排列的个数,叫做从
n
个不同元素中取出
m
个元素的排列数.
排列与排列数的区别:
排
列:是有序的元素列,不是数
排列数:排列的个数,是数
A
m
n
互动解疑
记作:
问题2中:
问题1中:
思考:你能否得出
的意义和
的值?
排列数为
3×2=6
种
排列数为
4×3×2=24
种
互动解疑
A
2
n
A
2
n
问题3
从n个不同元素中取出2个元素,排成一列,共有多少种排列方法?
问题4
从n个不同元素中取出3个元素,排成一列,共有多少种排列方法?
n种
(n-1)种
n种
(n-1)种
(n-2)种
互动解疑
=n
(n-1)
A
2
n
=n
(n-1)
(n-2)
A
3
n
问题5
从n个不同元素中取出m个元素,排成一列,共有多少种排列方法?
n种
(n-1)种
(n-2)种
(n-m+1)种
…
…
互动解疑
排列数公式:
公式的特征:右边第一个因数是n
,后面每个因数比前一个少1,最后一个因数是n-m+1,共有m个因数
n种
(n-1)种
(n-2)种
(n-m+1)种
…
…
互动解疑
A
n
n
(n的阶乘)
规定:
排列数公式:
排列数:
内化迁移
例3
(1)从5本不同的书中选3本送给3名同学,每人各1本,共有多少种不同的送法?
(种)
(种)
(2)从5种不同的书中买3本送给3名同学,每人各1本,共有多少种不同的送法?
内化迁移
【排列】
关键点:先取后排
【排列数】所有不同排列的个数
【排列数公式】
课堂小结
课堂检测
课后作业
谢谢!
