人教版八年级下册数学18.1平行四边形专项训练(word版含答案)
文档属性
| 名称 | 人教版八年级下册数学18.1平行四边形专项训练(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 08:09:44 | ||
图片预览




文档简介
18.1《平行四边形》专项训练
一.选择题(共15小题,每小题2分,共30分)
1.若平行四边形的一组邻边的长分别为5和8,则该平行四边形的周长为( )
A.13
B.16
C.22
D.26
2.在下列条件中,不能判定四边形为平行四边形的是( )
A.一组对边平行且相等
B.两组对边分别平行
C.一组对边平行,另一组对边相等
D.对角线互相平分
3.?ABCD中,∠D=130°,则∠B=( )
A.40°
B.50°
C.140°
D.130°
4.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD,AD=BC
B.∠BAD=∠BCD,∠ABC=∠ADC
C.OA=OC,OB=OD
D.AD=BC,AB∥CD
5.若平行四边形两个内角的度数比为1:2,则其中较大内角的度数为( )
A.100°
B.110°
C.120°
D.135°
6.如图,有两种说法:
①线段AB的长是点A到点B的距离.
②线段AB的长是直线l1、l2之间的距离.
关于这两种说法,正确的是 )
A.①正确,②错误
B.①正确,②正确
C.①错误,②正确
D.①错误,②错误
7.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=6,BC=10,则EF长为( )
A.1
B.2
C.3
D.4
8.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,则BF的长为( )
A.4
B.2
C.3
D.4
9.如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是( )
A.16
B.14
C.20
D.24
10.在?ABCD中,∠A与∠B的大小比是2:1,则∠C和∠D的大小分别是( )
A.60°和30°
B.120°和60°
C.240°和120°
D.150°和30°
11.如图,在平面直角坐标系x
O
y中,A(0,1),B(0,﹣1),C(3,0).若以A、B、C、D为顶点的四边形是平行四边形,所有符合条件的D点坐标是( )
A.(﹣3,0)
B.(3,﹣2),(﹣3,0)
C.(3,2),(3,﹣2)
D.(﹣3,0),(3,﹣2),(3,2)
12.已知:四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC
B.AB=CD,AD=BC
C.AO=CO,BO=DO
D.∠ABD=∠CDB,∠ADB=∠CBD
13.下列说法不正确的是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
14.如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于E,AD=3,AB=5,则EC的长为( )
A.1
B.2
C.3
D.5
15.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( )
A.4,4,8,8
B.5,5,7,7
C.4,8,4,8
D.5,7,5,7
二.填空题(共10小题,每小题2分,共20分)
16.已知?ABCD的三个顶点:点A(4,﹣1)、B(﹣1,1)、C(2,3),则第四个顶点D的坐标是
.
17.如图:已知?ABCD的对角线AC、BD相交于点O,AC=24cm,BD=38cm,AD=14cm,那么△OBC的周长为
cm.
18.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,则AB+BC的长为
.
19.?ABCD中,∠C=∠B+∠D,则∠A=
.
20.如图,已知四边形ABCD,对角线AC和BD相交于O,已知AB∥CD,则添加一个条件
可得出四边形ABCD是平行四边形.
21.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D为BC上一动点(不与点C重合),以AD,CD为一组邻边作平行四边形ADCE,当DE的值最小时,平行四边形ADCE周长为
.
22.如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=4m,则A、B两点间的距离是
m.
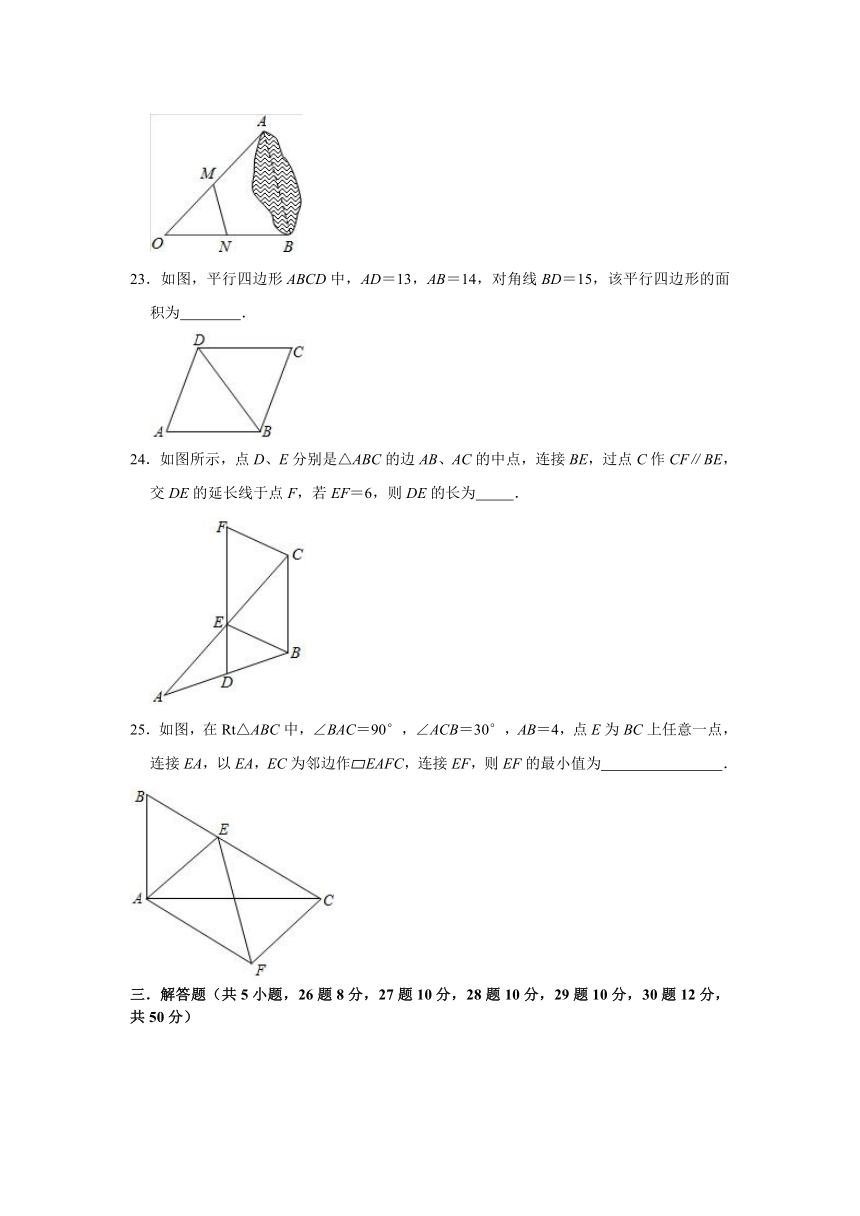
23.如图,平行四边形ABCD中,AD=13,AB=14,对角线BD=15,该平行四边形的面积为
.
24.如图所示,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=6,则DE的长为
.
25.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,AB=4,点E为BC上任意一点,连接EA,以EA,EC为邻边作?EAFC,连接EF,则EF的最小值为
.
解答题(共5小题,26题8分,27题10分,28题10分,29题10分,30题12分,共50分)
26.如图,在四边形ABCD中,AD∥BC.AE⊥AD交BD于点E.CF⊥BC交BD于点F.AE=CF.
求证:BE=DF.
27.如图,在?ABCD中,∠BAD的平分线AE交DC于E,∠DAE=25°.
(1)求∠C、∠B的度数;
(2)若BC=5,AB=8,求CE的长.
28.如图,在?ABCD中,E,F是对角线BD上的点,且BE=DF,求证:四边形AECF是平行四边形.
29.如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,延长AE,CF分别交CD,AB于点M,N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求△BFN的周长.
30.如图,在?ABCD,点E为AD的中点,延长BE、CD交于点F,连接AF,BD,CE.
(1)求证:四边形ABDF为平行四边形.
(2)若BE为∠ABC的角平分线,AB=5,CE=6,求△AEF的面积.
参考答案与试题解析
选择题(共15小题)
D
C
D
D
C
B
B
C
C
B
D
A
B
B
B
(7,1)或(1,﹣3)或(﹣3,5).
45.
14.
120°
AB=CD(答案不唯一).
4+2
8
168
3
证明:∵AD∥BC,
∴∠ADE=∠CBF,
∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴DE=BF,
∴DE﹣EF=BF﹣EF,即BE=DF.
解:(1)在?ABCD中,∠BAD的平分线AE交DC于E,∠DAE=25°,
∴∠DAE=∠EAB=∠DEA=25°,
∴∠DAB=∠C=50°,
∴∠B=180°﹣50°=130°,
(2)∵∠DAE=∠DEA,
∴DE=AD,
∵在?ABCD中,BC=5,AB=8,
∴AD=BC=5,CD=AB=8,
∴EC=CD﹣DE=8﹣5=3,
∴CE的长是3.
证明:连接EC、AF,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,且AB=CD,
∴AE∥FC,
∵BE=DF,
∴AE=FC,
∴四边形AECF是平行四边形.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AM⊥BD,CN⊥BD,
∴AM∥CN,
∴四边形CMAN是平行四边形;
(2)解:∵四边形CMAN是平行四边形,
∴AN=CM,
∵CD=AB,
∴DM=BN,
∵CD∥AB,
∴∠MDE=∠NBF,
在△BNF和△DME中,
,
∴△DME≌△BNF(AAS),
∴BF=DE=4,
在Rt△BFN中,BN===5,
∴△BFN的周长=FN+BF+BN=3+4+5=12.
解:(1)证明:由题意得,AB∥CF,
∴∠ABE=∠DFE,
又∵点E为AD的中点,
∴AE=DE,
在△ABE和△DFE中,
,
∴△ABE≌△DFE(AAS)
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF为平行四边形(一组对边平行且相等的四边形是平行四边形);
(2)过点F作AD的垂线交AD延长线于点K,过点D作DH⊥EC,过点E作EG⊥CD,
∵S△AEF=;,
∴S△AEF=S△EDF,
又∵BE为∠ABC的角平分线,
∴∠ABE=∠EBC,
又∵AD∥BC,
∴∠EBC=∠FED,
而∠ABE=∠DFE,
∴∠FED=∠DFE,
∴ED=FD,
由(1)可知AB=DC=FD=5,
∴ED=FD=DC=5,
又∵S△EFD=,S△EDC=,
∴S△AEF=S△EDF=S△ECD,
在等腰△EDC中,ED=CD=5,EC=6,
∵DH⊥EC,
∴EH===3,
在Rt△EHD中,ED=5,EH=3,
∴DH===4,
∴S△ECD==12,
∴S△AEF=S△EDF=S△ECD=12,
故S△AEF=12.
一.选择题(共15小题,每小题2分,共30分)
1.若平行四边形的一组邻边的长分别为5和8,则该平行四边形的周长为( )
A.13
B.16
C.22
D.26
2.在下列条件中,不能判定四边形为平行四边形的是( )
A.一组对边平行且相等
B.两组对边分别平行
C.一组对边平行,另一组对边相等
D.对角线互相平分
3.?ABCD中,∠D=130°,则∠B=( )
A.40°
B.50°
C.140°
D.130°
4.不能判定四边形ABCD为平行四边形的题设是( )
A.AB=CD,AD=BC
B.∠BAD=∠BCD,∠ABC=∠ADC
C.OA=OC,OB=OD
D.AD=BC,AB∥CD
5.若平行四边形两个内角的度数比为1:2,则其中较大内角的度数为( )
A.100°
B.110°
C.120°
D.135°
6.如图,有两种说法:
①线段AB的长是点A到点B的距离.
②线段AB的长是直线l1、l2之间的距离.
关于这两种说法,正确的是 )
A.①正确,②错误
B.①正确,②正确
C.①错误,②正确
D.①错误,②错误
7.如图,在?ABCD中,BF平分∠ABC,交AD于点F,CE平分∠BCD交AD于点E,AB=6,BC=10,则EF长为( )
A.1
B.2
C.3
D.4
8.如图,在△ABC中,点D,E分别是边AB,AC的中点,AF⊥BC,垂足为点F,∠ADE=30°,DF=3,则BF的长为( )
A.4
B.2
C.3
D.4
9.如图,在?ABCD中,DE平分∠ADC,AD=6,BE=2,则?ABCD的周长是( )
A.16
B.14
C.20
D.24
10.在?ABCD中,∠A与∠B的大小比是2:1,则∠C和∠D的大小分别是( )
A.60°和30°
B.120°和60°
C.240°和120°
D.150°和30°
11.如图,在平面直角坐标系x
O
y中,A(0,1),B(0,﹣1),C(3,0).若以A、B、C、D为顶点的四边形是平行四边形,所有符合条件的D点坐标是( )
A.(﹣3,0)
B.(3,﹣2),(﹣3,0)
C.(3,2),(3,﹣2)
D.(﹣3,0),(3,﹣2),(3,2)
12.已知:四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
A.AB∥CD,AD=BC
B.AB=CD,AD=BC
C.AO=CO,BO=DO
D.∠ABD=∠CDB,∠ADB=∠CBD
13.下列说法不正确的是( )
A.两组对边分别平行的四边形是平行四边形
B.一组对边平行,另一组对边相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边平行,一组对角相等的四边形是平行四边形
14.如图,在平行四边形ABCD中,AE平分∠BAD,交CD边于E,AD=3,AB=5,则EC的长为( )
A.1
B.2
C.3
D.5
15.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为( )
A.4,4,8,8
B.5,5,7,7
C.4,8,4,8
D.5,7,5,7
二.填空题(共10小题,每小题2分,共20分)
16.已知?ABCD的三个顶点:点A(4,﹣1)、B(﹣1,1)、C(2,3),则第四个顶点D的坐标是
.
17.如图:已知?ABCD的对角线AC、BD相交于点O,AC=24cm,BD=38cm,AD=14cm,那么△OBC的周长为
cm.
18.如图,在△ABC中,D,E,F分别是边AB,BC,CA的中点,四边形BEFD周长为14,则AB+BC的长为
.
19.?ABCD中,∠C=∠B+∠D,则∠A=
.
20.如图,已知四边形ABCD,对角线AC和BD相交于O,已知AB∥CD,则添加一个条件
可得出四边形ABCD是平行四边形.
21.如图,在Rt△ABC中,∠B=90°,AB=3,BC=4,点D为BC上一动点(不与点C重合),以AD,CD为一组邻边作平行四边形ADCE,当DE的值最小时,平行四边形ADCE周长为
.
22.如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=4m,则A、B两点间的距离是
m.
23.如图,平行四边形ABCD中,AD=13,AB=14,对角线BD=15,该平行四边形的面积为
.
24.如图所示,点D、E分别是△ABC的边AB、AC的中点,连接BE,过点C作CF∥BE,交DE的延长线于点F,若EF=6,则DE的长为
.
25.如图,在Rt△ABC中,∠BAC=90°,∠ACB=30°,AB=4,点E为BC上任意一点,连接EA,以EA,EC为邻边作?EAFC,连接EF,则EF的最小值为
.
解答题(共5小题,26题8分,27题10分,28题10分,29题10分,30题12分,共50分)
26.如图,在四边形ABCD中,AD∥BC.AE⊥AD交BD于点E.CF⊥BC交BD于点F.AE=CF.
求证:BE=DF.
27.如图,在?ABCD中,∠BAD的平分线AE交DC于E,∠DAE=25°.
(1)求∠C、∠B的度数;
(2)若BC=5,AB=8,求CE的长.
28.如图,在?ABCD中,E,F是对角线BD上的点,且BE=DF,求证:四边形AECF是平行四边形.
29.如图,已知四边形ABCD是平行四边形,AE⊥BD于点E,CF⊥BD于点F,延长AE,CF分别交CD,AB于点M,N.
(1)求证:四边形CMAN是平行四边形;
(2)已知DE=4,FN=3,求△BFN的周长.
30.如图,在?ABCD,点E为AD的中点,延长BE、CD交于点F,连接AF,BD,CE.
(1)求证:四边形ABDF为平行四边形.
(2)若BE为∠ABC的角平分线,AB=5,CE=6,求△AEF的面积.
参考答案与试题解析
选择题(共15小题)
D
C
D
D
C
B
B
C
C
B
D
A
B
B
B
(7,1)或(1,﹣3)或(﹣3,5).
45.
14.
120°
AB=CD(答案不唯一).
4+2
8
168
3
证明:∵AD∥BC,
∴∠ADE=∠CBF,
∵AE⊥AD,CF⊥BC,
∴∠EAD=∠FCB=90°,
在△ADE和△CBF中,
,
∴△ADE≌△CBF(AAS),
∴DE=BF,
∴DE﹣EF=BF﹣EF,即BE=DF.
解:(1)在?ABCD中,∠BAD的平分线AE交DC于E,∠DAE=25°,
∴∠DAE=∠EAB=∠DEA=25°,
∴∠DAB=∠C=50°,
∴∠B=180°﹣50°=130°,
(2)∵∠DAE=∠DEA,
∴DE=AD,
∵在?ABCD中,BC=5,AB=8,
∴AD=BC=5,CD=AB=8,
∴EC=CD﹣DE=8﹣5=3,
∴CE的长是3.
证明:连接EC、AF,如图所示:
∵四边形ABCD是平行四边形,
∴AB∥CD,且AB=CD,
∴AE∥FC,
∵BE=DF,
∴AE=FC,
∴四边形AECF是平行四边形.
(1)证明:∵四边形ABCD是平行四边形,
∴AB∥CD,
∵AM⊥BD,CN⊥BD,
∴AM∥CN,
∴四边形CMAN是平行四边形;
(2)解:∵四边形CMAN是平行四边形,
∴AN=CM,
∵CD=AB,
∴DM=BN,
∵CD∥AB,
∴∠MDE=∠NBF,
在△BNF和△DME中,
,
∴△DME≌△BNF(AAS),
∴BF=DE=4,
在Rt△BFN中,BN===5,
∴△BFN的周长=FN+BF+BN=3+4+5=12.
解:(1)证明:由题意得,AB∥CF,
∴∠ABE=∠DFE,
又∵点E为AD的中点,
∴AE=DE,
在△ABE和△DFE中,
,
∴△ABE≌△DFE(AAS)
∴AB=DF,
又∵AB∥DF,
∴四边形ABDF为平行四边形(一组对边平行且相等的四边形是平行四边形);
(2)过点F作AD的垂线交AD延长线于点K,过点D作DH⊥EC,过点E作EG⊥CD,
∵S△AEF=;,
∴S△AEF=S△EDF,
又∵BE为∠ABC的角平分线,
∴∠ABE=∠EBC,
又∵AD∥BC,
∴∠EBC=∠FED,
而∠ABE=∠DFE,
∴∠FED=∠DFE,
∴ED=FD,
由(1)可知AB=DC=FD=5,
∴ED=FD=DC=5,
又∵S△EFD=,S△EDC=,
∴S△AEF=S△EDF=S△ECD,
在等腰△EDC中,ED=CD=5,EC=6,
∵DH⊥EC,
∴EH===3,
在Rt△EHD中,ED=5,EH=3,
∴DH===4,
∴S△ECD==12,
∴S△AEF=S△EDF=S△ECD=12,
故S△AEF=12.
