人教版八年级下册数学18.2特殊的平行四边形试题(word版含答案)
文档属性
| 名称 | 人教版八年级下册数学18.2特殊的平行四边形试题(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 103.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 08:28:33 | ||
图片预览


文档简介
18.2《特殊的平行四边形》专项训练
一.选择题(共15小题,每小题2分,共30分)
1.如图所示,在正方形ABCD中,E为CD边中点,连接AE,对角线BD交AE于点F,已知EF=1,则线段AE的长度为( )
A.2
B.3
C.4
D.5
2.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长为( )
A.24
B.18
C.12
D.9
3.如图,Rt△ABC中,∠ACB=90°,AB=10,D是AB的中点,则CD的长为( )
A.5
B.6
C.8
D.10
4.在四边形ABCD中,AC、BD交于点O,则下列不能判断四边形ABCD是矩形的是( )
A.∠A=∠B=∠C=∠D
B.OA=OB=OC=OD
C.AB=CD,AD=BC,AC=BD
D.∠A=∠C,∠B+∠C=180°,∠AOB=∠BOC
5.如图,在矩形ABCD中,对角线AC与BD相交于点O,EO⊥AC于点O,交BC于点E,若△ABE的周长为5,AB=2,则AD的长为( )
A.2
B.2.5
C.3
D.4
6.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10
B.8
C.6
D.4
7.矩形具有而菱形不一定具有的性质是( )
A.两组对边分别平行
B.对角线平分一组对角
C.对角线互相垂直
D.对角线相等
8.下列命题是真命题的是( )
A.平行四边形对角线平分对角
B.菱形的对角线相等
C.对角线互相垂直的平行四边形是菱形
D.对角线相等的四边形是矩形
9.菱形,矩形,正方形都具有的性质是( )
A.四条边相等,四个角相等
B.对角线相等
C.对角线互相垂直
D.对角线互相平分
10.A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点
B.BC中点
C.AC中点
D.∠C的平分线与AB的交点
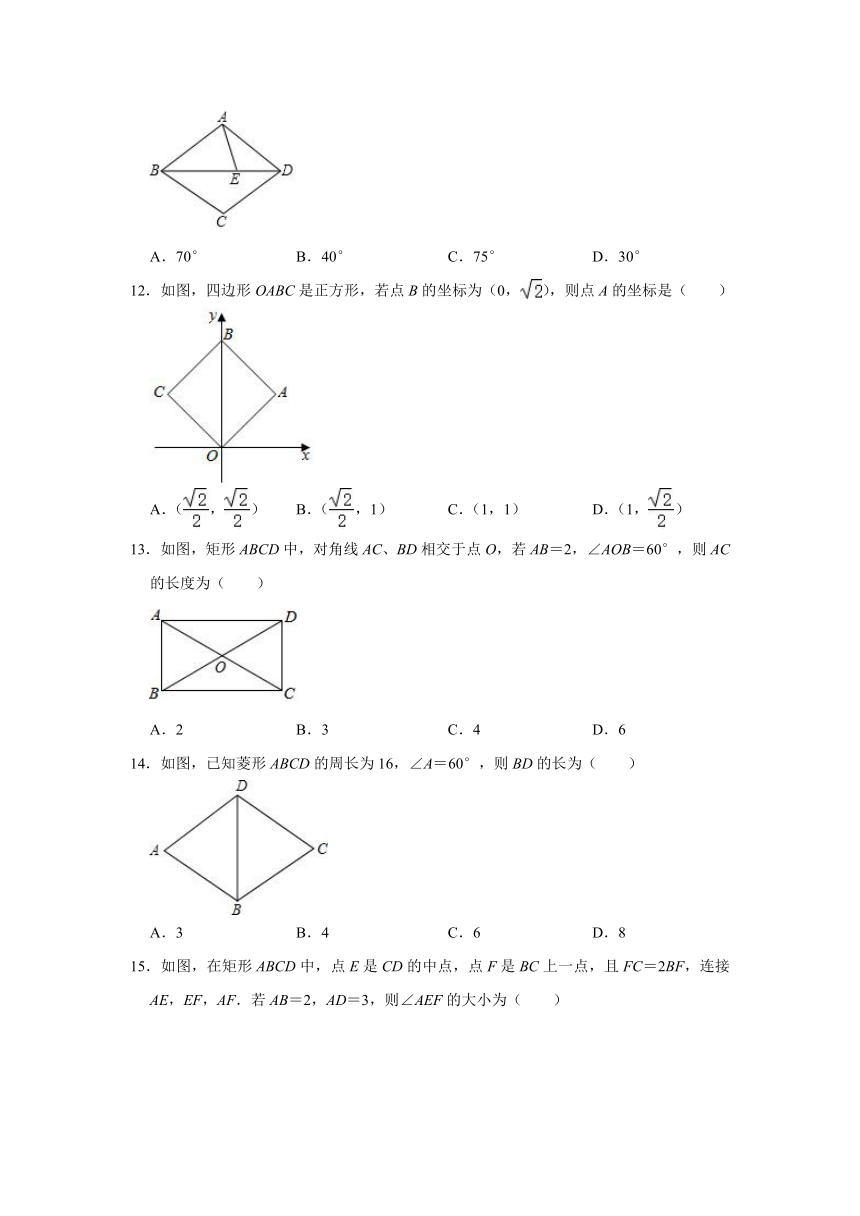
11.在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE=( )
A.70°
B.40°
C.75°
D.30°
12.如图,四边形OABC是正方形,若点B的坐标为(0,),则点A的坐标是( )
A.(,)
B.(,1)
C.(1,1)
D.(1,)
13.如图,矩形ABCD中,对角线AC、BD相交于点O,若AB=2,∠AOB=60°,则AC的长度为( )
A.2
B.3
C.4
D.6
14.如图,已知菱形ABCD的周长为16,∠A=60°,则BD的长为( )
A.3
B.4
C.6
D.8
15.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF,AF.若AB=2,AD=3,则∠AEF的大小为( )
A.30°
B.45°
C.60°
D.不能确定
二.填空题(共10小题,每小题2分,共20分)
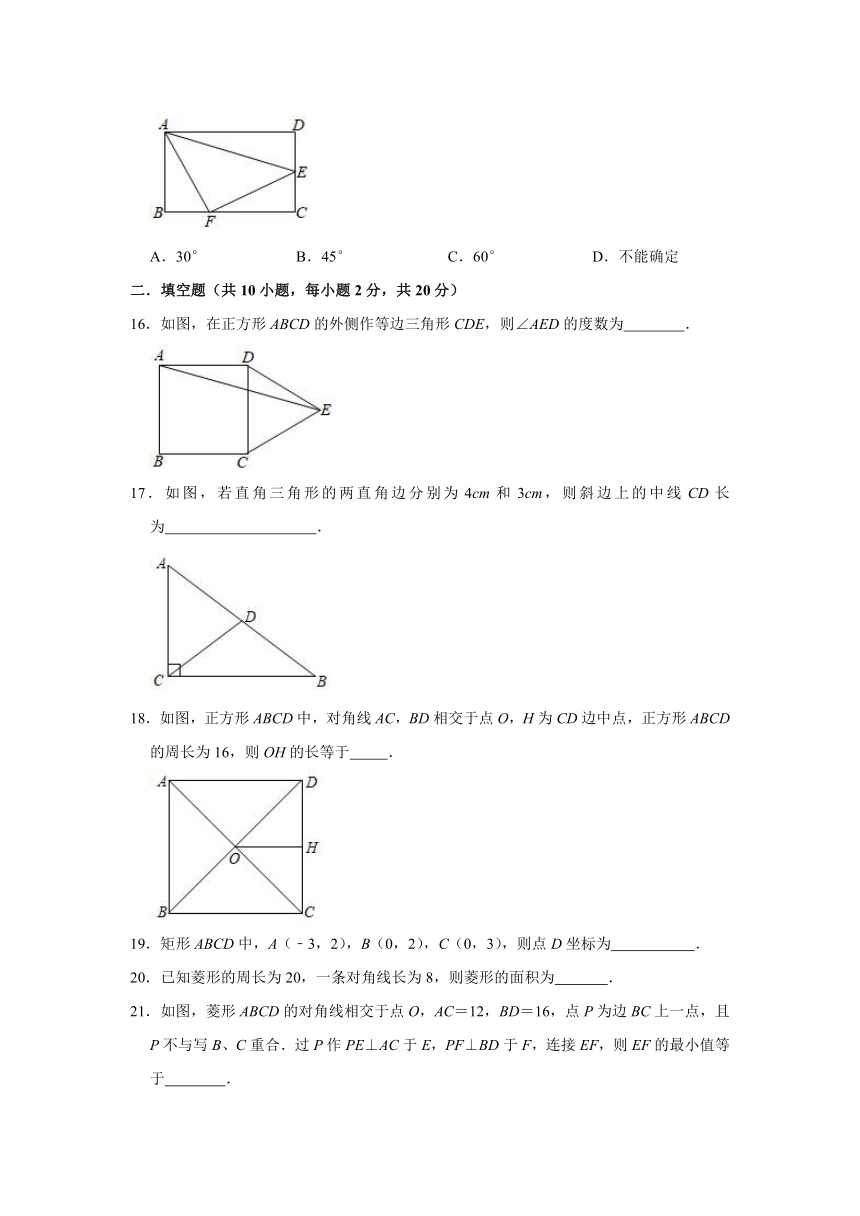
16.如图,在正方形ABCD的外侧作等边三角形CDE,则∠AED的度数为
.
17.如图,若直角三角形的两直角边分别为4cm和3cm,则斜边上的中线CD长为
.
18.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为16,则OH的长等于
.
19.矩形ABCD中,A(﹣3,2),B(0,2),C(0,3),则点D坐标为
.
20.已知菱形的周长为20,一条对角线长为8,则菱形的面积为
.
21.如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与写B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连接EF,则EF的最小值等于
.
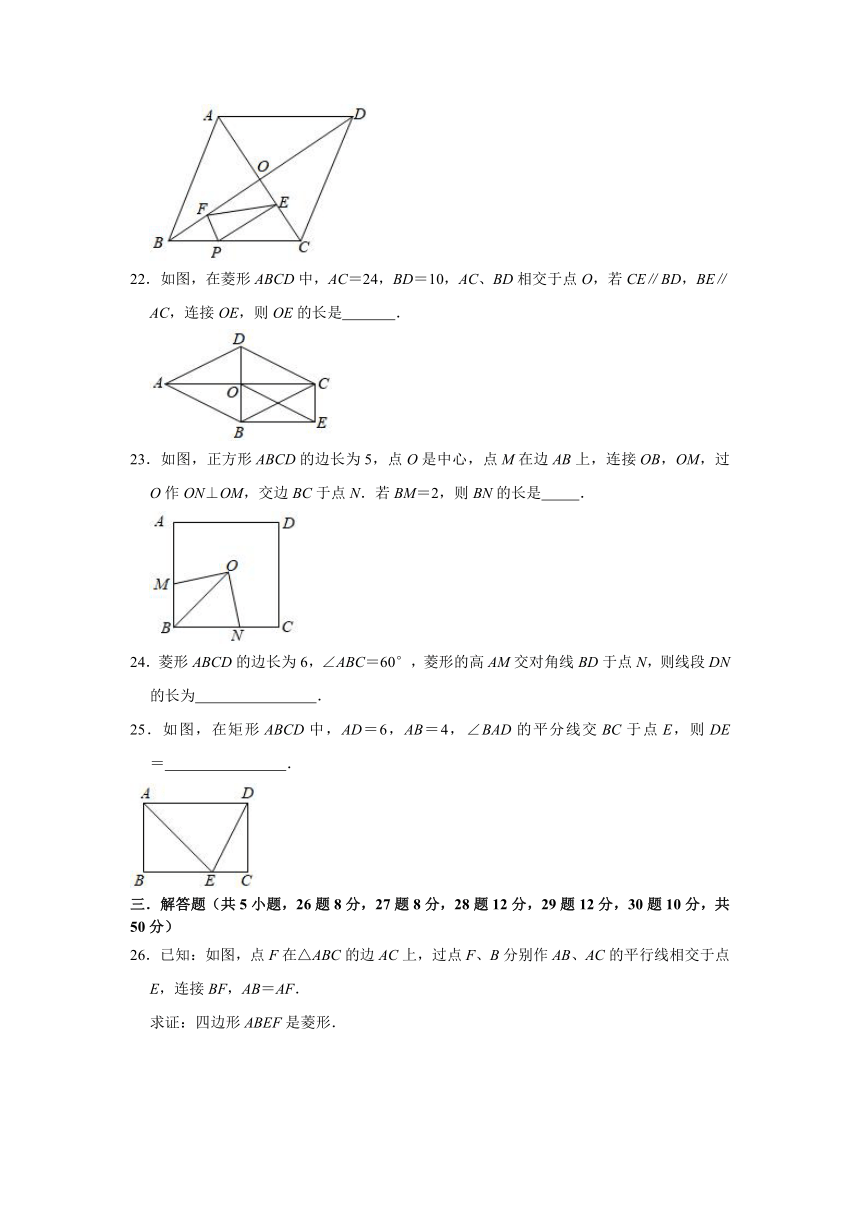
22.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE∥BD,BE∥AC,连接OE,则OE的长是
.
23.如图,正方形ABCD的边长为5,点O是中心,点M在边AB上,连接OB,OM,过O作ON⊥OM,交边BC于点N.若BM=2,则BN的长是
.
24.菱形ABCD的边长为6,∠ABC=60°,菱形的高AM交对角线BD于点N,则线段DN的长为
.
25.如图,在矩形ABCD中,AD=6,AB=4,∠BAD的平分线交BC于点E,则DE=
.
解答题(共5小题,26题8分,27题8分,28题12分,29题12分,30题10分,共50分)
26.已知:如图,点F在△ABC的边AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,AB=AF.
求证:四边形ABEF是菱形.
27.如图,正方形ABCD的边长是4,BE=CE,DF=3CF.证明:∠AEF=90°.
28.如图,在正方形ABCD中,点E在边BC上,AE交BD于点F,DG⊥AE于G,∠DGE的平分线GH分别交BD,CD于点P,H,连接FH.
(1)求证:∠DHG=∠DFA;
(2)求证:FH∥BC;
(3)求:的值.
29.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
30.如图,菱形ABCD的对角线AC,BD交于点O,且BE∥AC,AE∥BD,连接EO.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若CD=6,求OE的长.
参考答案与试题解析
B
A
A
D
C
B
D
C
D
A
A
A
C
B
B
15°
cm
2
(﹣3,3)
24
4.8
13
3
4
2
证明:∵EF∥AB,BE∥AF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴?ABEF是菱形.
证明:连接AF,
∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,
∵正方形ABCD的边长是4,BE=CE,DF=3CF.
∴BE=CE=2,CF=1,DF=3,
由勾股定理得,
AE2=AB2+BE2=42+22=20,
EF2=CE2+CF2=22+12=5,
AF2=AD2+DF2=42+32=25,
又∵AE2+EF2=AF2,
∴△AEF是直角三角形,即∠AEF=90°
证明:(1)∵四边形ABCD是正方形,
∴∠BDC=45°,
∵DG⊥AE,
∴∠DGE=90°,
∵GH平分∠DGE,
∴∠DGH=∠EGH=45°,
∴∠BDC=∠EGH=45°,
∵∠DPH=∠GPF,
∴∠DHG=∠DFA.
(2)由(1)可知:∠BDC=∠EGH=45°,∠DPH=∠GPF,
∴△GPF∽△DPH,
∴,
∴,
又∵∠GPD=∠FPH,
∴△GPD∽△FPH,
∴∠DGP=∠HFP=45°,又∠DBC=45°,
∴∠DBC=∠HFP=45°,
∴FH∥BC.
(3)连接PA,过点P作PM⊥AE于M,PN⊥DG于N,QP⊥GP交GD于Q,如图所示.
由(2)证法,易证∠PAG=∠PDG,
∵PM⊥AE,PN⊥DG,GH平分∠DGE,
∴PM=PN,
∴Rt△PMA≌Rt△PND(AAS),
∴PA=PD,
∵四边形ABCD是正方形,∠ADB=45°,
∴∠APD=90°=∠GPQ,
∴∠APG=∠DPQ,
∴△APG≌△DPQ(ASA),
∴QD=AG,
∵∠PGQ=45°,
∴△PGQ是等腰直角三角形,
∴GQ=PG,
∴DG﹣AG=DG﹣DQ=GQ=PG,
∴.
(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)解:当∠A=45°时,四边形BECD是正方形,
理由:∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
解:(1)四边形AEBO是矩形.
理由:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形,
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,
即∠AOB=90°,
∴四边形AEBO是矩形;
(2)∵四边形AEBO是矩形,
∴EO=AB,
∵四边形ABCD是菱形,
∴AB=CD.
∴EO=CD=6.
一.选择题(共15小题,每小题2分,共30分)
1.如图所示,在正方形ABCD中,E为CD边中点,连接AE,对角线BD交AE于点F,已知EF=1,则线段AE的长度为( )
A.2
B.3
C.4
D.5
2.如图,菱形ABCD中,E、F分别是AB、AC的中点,若EF=3,则菱形ABCD的周长为( )
A.24
B.18
C.12
D.9
3.如图,Rt△ABC中,∠ACB=90°,AB=10,D是AB的中点,则CD的长为( )
A.5
B.6
C.8
D.10
4.在四边形ABCD中,AC、BD交于点O,则下列不能判断四边形ABCD是矩形的是( )
A.∠A=∠B=∠C=∠D
B.OA=OB=OC=OD
C.AB=CD,AD=BC,AC=BD
D.∠A=∠C,∠B+∠C=180°,∠AOB=∠BOC
5.如图,在矩形ABCD中,对角线AC与BD相交于点O,EO⊥AC于点O,交BC于点E,若△ABE的周长为5,AB=2,则AD的长为( )
A.2
B.2.5
C.3
D.4
6.如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的一点,ED平分∠AEC,则BE的长为( )
A.10
B.8
C.6
D.4
7.矩形具有而菱形不一定具有的性质是( )
A.两组对边分别平行
B.对角线平分一组对角
C.对角线互相垂直
D.对角线相等
8.下列命题是真命题的是( )
A.平行四边形对角线平分对角
B.菱形的对角线相等
C.对角线互相垂直的平行四边形是菱形
D.对角线相等的四边形是矩形
9.菱形,矩形,正方形都具有的性质是( )
A.四条边相等,四个角相等
B.对角线相等
C.对角线互相垂直
D.对角线互相平分
10.A、B、C分别表示三个村庄,AB=1000米,BC=600米,AC=800米,为拟建一个文化活动中心,要求这三个村庄到活动中心的距离相等,则活动中心P的位置应在( )
A.AB中点
B.BC中点
C.AC中点
D.∠C的平分线与AB的交点
11.在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE=( )
A.70°
B.40°
C.75°
D.30°
12.如图,四边形OABC是正方形,若点B的坐标为(0,),则点A的坐标是( )
A.(,)
B.(,1)
C.(1,1)
D.(1,)
13.如图,矩形ABCD中,对角线AC、BD相交于点O,若AB=2,∠AOB=60°,则AC的长度为( )
A.2
B.3
C.4
D.6
14.如图,已知菱形ABCD的周长为16,∠A=60°,则BD的长为( )
A.3
B.4
C.6
D.8
15.如图,在矩形ABCD中,点E是CD的中点,点F是BC上一点,且FC=2BF,连接AE,EF,AF.若AB=2,AD=3,则∠AEF的大小为( )
A.30°
B.45°
C.60°
D.不能确定
二.填空题(共10小题,每小题2分,共20分)
16.如图,在正方形ABCD的外侧作等边三角形CDE,则∠AED的度数为
.
17.如图,若直角三角形的两直角边分别为4cm和3cm,则斜边上的中线CD长为
.
18.如图,正方形ABCD中,对角线AC,BD相交于点O,H为CD边中点,正方形ABCD的周长为16,则OH的长等于
.
19.矩形ABCD中,A(﹣3,2),B(0,2),C(0,3),则点D坐标为
.
20.已知菱形的周长为20,一条对角线长为8,则菱形的面积为
.
21.如图,菱形ABCD的对角线相交于点O,AC=12,BD=16,点P为边BC上一点,且P不与写B、C重合.过P作PE⊥AC于E,PF⊥BD于F,连接EF,则EF的最小值等于
.
22.如图,在菱形ABCD中,AC=24,BD=10,AC、BD相交于点O,若CE∥BD,BE∥AC,连接OE,则OE的长是
.
23.如图,正方形ABCD的边长为5,点O是中心,点M在边AB上,连接OB,OM,过O作ON⊥OM,交边BC于点N.若BM=2,则BN的长是
.
24.菱形ABCD的边长为6,∠ABC=60°,菱形的高AM交对角线BD于点N,则线段DN的长为
.
25.如图,在矩形ABCD中,AD=6,AB=4,∠BAD的平分线交BC于点E,则DE=
.
解答题(共5小题,26题8分,27题8分,28题12分,29题12分,30题10分,共50分)
26.已知:如图,点F在△ABC的边AC上,过点F、B分别作AB、AC的平行线相交于点E,连接BF,AB=AF.
求证:四边形ABEF是菱形.
27.如图,正方形ABCD的边长是4,BE=CE,DF=3CF.证明:∠AEF=90°.
28.如图,在正方形ABCD中,点E在边BC上,AE交BD于点F,DG⊥AE于G,∠DGE的平分线GH分别交BD,CD于点P,H,连接FH.
(1)求证:∠DHG=∠DFA;
(2)求证:FH∥BC;
(3)求:的值.
29.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,垂足为F,交直线MN于E,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)在满足(2)的条件下,当△ABC满足什么条件时,四边形BECD是正方形?(不必说明理由)
30.如图,菱形ABCD的对角线AC,BD交于点O,且BE∥AC,AE∥BD,连接EO.
(1)试判断四边形AEBO的形状,并说明理由;
(2)若CD=6,求OE的长.
参考答案与试题解析
B
A
A
D
C
B
D
C
D
A
A
A
C
B
B
15°
cm
2
(﹣3,3)
24
4.8
13
3
4
2
证明:∵EF∥AB,BE∥AF,
∴四边形ABEF是平行四边形,
∵AB=AF,
∴?ABEF是菱形.
证明:连接AF,
∵四边形ABCD是正方形,
∴∠B=∠C=∠D=90°,
∵正方形ABCD的边长是4,BE=CE,DF=3CF.
∴BE=CE=2,CF=1,DF=3,
由勾股定理得,
AE2=AB2+BE2=42+22=20,
EF2=CE2+CF2=22+12=5,
AF2=AD2+DF2=42+32=25,
又∵AE2+EF2=AF2,
∴△AEF是直角三角形,即∠AEF=90°
证明:(1)∵四边形ABCD是正方形,
∴∠BDC=45°,
∵DG⊥AE,
∴∠DGE=90°,
∵GH平分∠DGE,
∴∠DGH=∠EGH=45°,
∴∠BDC=∠EGH=45°,
∵∠DPH=∠GPF,
∴∠DHG=∠DFA.
(2)由(1)可知:∠BDC=∠EGH=45°,∠DPH=∠GPF,
∴△GPF∽△DPH,
∴,
∴,
又∵∠GPD=∠FPH,
∴△GPD∽△FPH,
∴∠DGP=∠HFP=45°,又∠DBC=45°,
∴∠DBC=∠HFP=45°,
∴FH∥BC.
(3)连接PA,过点P作PM⊥AE于M,PN⊥DG于N,QP⊥GP交GD于Q,如图所示.
由(2)证法,易证∠PAG=∠PDG,
∵PM⊥AE,PN⊥DG,GH平分∠DGE,
∴PM=PN,
∴Rt△PMA≌Rt△PND(AAS),
∴PA=PD,
∵四边形ABCD是正方形,∠ADB=45°,
∴∠APD=90°=∠GPQ,
∴∠APG=∠DPQ,
∴△APG≌△DPQ(ASA),
∴QD=AG,
∵∠PGQ=45°,
∴△PGQ是等腰直角三角形,
∴GQ=PG,
∴DG﹣AG=DG﹣DQ=GQ=PG,
∴.
(1)证明:∵DE⊥BC,
∴∠DFB=90°,
∵∠ACB=90°,
∴∠ACB=∠DFB,
∴AC∥DE,
∵MN∥AB,即CE∥AD,
∴四边形ADEC是平行四边形,
∴CE=AD;
(2)解:四边形BECD是菱形,
理由是:∵D为AB中点,
∴AD=BD,
∵CE=AD,
∴BD=CE,
∵BD∥CE,
∴四边形BECD是平行四边形,
∵∠ACB=90°,D为AB中点,
∴CD=BD,
∴四边形BECD是菱形;
(3)解:当∠A=45°时,四边形BECD是正方形,
理由:∵∠ACB=90°,
∴∠ABC=45°,
由(2)可知,四边形BECD是菱形,
∴∠ABC=∠CBE=45°,
∴∠DBE=90°,
∴四边形BECD是正方形.
解:(1)四边形AEBO是矩形.
理由:∵BE∥AC,AE∥BD,
∴四边形AEBO是平行四边形,
又∵菱形ABCD对角线交于点O,
∴AC⊥BD,
即∠AOB=90°,
∴四边形AEBO是矩形;
(2)∵四边形AEBO是矩形,
∴EO=AB,
∵四边形ABCD是菱形,
∴AB=CD.
∴EO=CD=6.
