六年级数学下册试题 一课一练《统计与概率--概率(可能性)》 人教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《统计与概率--概率(可能性)》 人教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 810.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 13:54:25 | ||
图片预览




文档简介
《统计与概率--概率(可能性)》
一、选择题(每题1分,共16分)
1.张阳给姑姑打电话.他只记得姑姑的电话号码是“862
6538”,他准确拨出电话的可能性是(?
)
A.
B.
C.
D.
2.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是(
)
A.
B.
C.
D.
3.在袋子里放4个黄球和1个白球(两种球除了颜色不同其余都相同),从中任意摸出一个球,下列说法正确的是(
)。
A.一定能摸到黄球
B.不可能摸到白球
C.摸到黄球和白球的可能性相等
D.摸到每个球的可能性相等
4.一个仅装有球的不透明布袋里共有4个红球,5个黑球和7个黄球,从中任意摸出一个球,摸到(
)的可能性最大。
A.红球
B.黄球
C.黑球
D.无法确定
5.用下面转盘做游戏,指针停在1号区域的可能性比停在4号区域的可能性(
)。
A.大
B.小
C.相等
D.不确定
6.从、、、四张卡片中任选两张组成一个两位数,组成的两位数中可能性最大的是(
)。
A.合数
B.质数
C.偶数
D.奇数
7.一个袋中装有一双红袜子和一双蓝袜子,任意摸出两只,能配成颜色相同的一双袜子的可能性是(
)。
A.
B.
C.
D.
8.小明任意买一张电影票,这张票的座位号在下列情况中可能性最小的是(
)。
A.座位号是偶数
B.座位号是2,22或222
C.座位号是10的倍数
D.座位号是10
9.小强把1—9的数字卡片共九张打乱顺序反扣在桌上,从中任意摸一张,摸到质数的可能性与摸到合数的可能性相比(
)。
A.摸到质数的可能性大
B.摸到合数的可能性大
C.摸到质数与摸到合数的可能性相等
D.无法确定
10.甲、乙两人做掷骰子游戏,骰子的六个面上分别标有1、2、3、4、5、6,下面(
)游戏规则是公平的。
A.质数甲贏,合数乙贏。
B.奇数甲贏,偶数乙贏。
C.小于3的甲贏,大于3的乙贏。
D.小于4的甲贏,大于4的乙贏。
11.如图,向标靶随意投一支飞标,如果投出的飞标都中靶,且投中每个方格的机会均等,那么投中涂色部分的可能性是(
)。
A.
B.
C.
12.有一种游戏的规则是:先旋转转盘的指针,如果指针箭头停在3的倍数的位置,就可以从盒子里摸出一个珠子。如果摸到黑色珠子就能得到奖品,东东玩了一次,他旋转转盘后,指针箭头所在位置和盒子里珠子的情况如下图所示。下面说法合理的是(
)。
A.他不可能得到奖品
B.他得到奖品的可能性小
C.他得到奖品的可能性大D.他一定可以得到奖品
13.小华和小敏玩掷骰子游戏,一起掷两个骰子,得到两个数,和是6小华得一分,和是12小敏得一分,和是其它数两人都不得分。掷20次,得分高的人获胜。这个游戏规则(
)。
A.公平,两人赢的可能性一样大
B.不公平,小华赢的可能性更大
C.不公平,小敏赢的可能性更大
D.无法确定
14.盒子里有8个球,球上分别标有2、3、4、5、6、7、8、9,优优和小贤两人玩摸球游戏,下面的规则中对双方都公平的是(
)。
A.任意摸一球,摸到质数优优胜,摸到合数小贤胜
B.任意摸一球,摸到的数小于5优优胜,摸到的数大于5小贤胜
C.任意摸一球,摸到2的倍数优优胜,摸到3的倍数小贤胜
D.任意摸一球,摸到4的因数优优胜,摸到5的因数小贤胜
15.任意抛掷两枚一元硬币,出现一正一反的机会是(
)。
A.
B.
C.
D.1
16.下列说法正确的是(????
)
A.彩票中奖的机会是1%,买100张一定能中奖.
B.从1、2、3、4、5这五个数字中任取一个数,取得奇数的可能性大.
C.可能性很小的事情在一次实验中一定不会发生.
D.一枚硬币,小明抛掷5次有4次正面向上,则抛掷一枚硬币正面向上的概率为0.8.
二、填空题(每题2分,共20分)
1.一个正方体,它的1个面上写着“1”,2个面上写着“2”,3个面上写着“3”,抛起这个正方体落下后,朝上的数是奇数的可能性是____。
2.要从甲、乙、丙、丁4人中抽签选出两人参加素质检测,恰好抽到甲、乙两人的可能性是(________)。
3.一个袋子里有2个黑球、4个红球和1个白球,任意摸一个球,摸到(________)球的可能性最大。要想保证摸到的一定是红球,至少需要摸出(________)个。
4.如图,任摸一个球,要使摸到黄球的可能性比白球大,盒子中至少应增加(________)个黄球。
5.新年联欢会用抽签决定表演的节目,抽签盒里有8张唱歌、5张朗诵、3张跳舞。小明任意抽一张,抽到(________)的可能性最大。
6.掷一个骰子,单数朝上的可能性是________,双数朝上的可能性是________。如果掷60次,“6”朝上的次数大约是________。
7.口袋里有1个白球和2个黄球,每个球除颜色外都相同,任意摸出一个球,摸到(______)球的可能性大,如果要使摸到两种球的可能性相等,那么需要再往口袋里放入(______)个(______)球。
8.王东和李阳用转盘(如图)玩游戏,转盘指针指向质数就是王东胜,指向合数就是李阳胜。在A、B处填上合适的数(不与转盘上的数相同),使这个游戏对双方都公平。A可以是(______),B可以是(______)。
9.在一个不透明的布袋中,装有白色小球10个、红色小球7个和若干个黑色小球,这些小球除颜色外其余都相同。要从布袋中随机摸出1个小球,若摸出的小球是黑色的可能性大于红色的可能性且小于白色的可能性,则布袋中的黑色小球可以有(______)个。
10.如图所示,分别向周长相等的圆和正方形内扔同样大小的石子儿,命中(________)形的可能性更大。
三、判断题(每题1分,共6分)
1.明天一定会下雨.(____)
2.一个袋子里装了形状、大小都相同的3个绿球和3个黄球,每次摸到1个球,摸到绿球和黄球的可能性大小是一样的。(________)
3.抛硬币时正面向上和反面向上的可能性是相等的,刚刚抛了20次,肯定有10次正面向上。(________)
4.口袋中有大小、材质相同的红球3个,白球4个和黑球5个,要想使从中摸出一个红球的可能性是,应该再往口袋中放8个红球。(______)
5.盒子中有10个白球、1个黄球,从中随意摸出一个球,如果是黄球,龙一鸣赢;如果是白球,依依赢。那么依依一定赢。(________)
6.一次抽奖活动的中奖率是百分之一,抽100次一定会中奖.
(______)
四.图形计算题(16分)
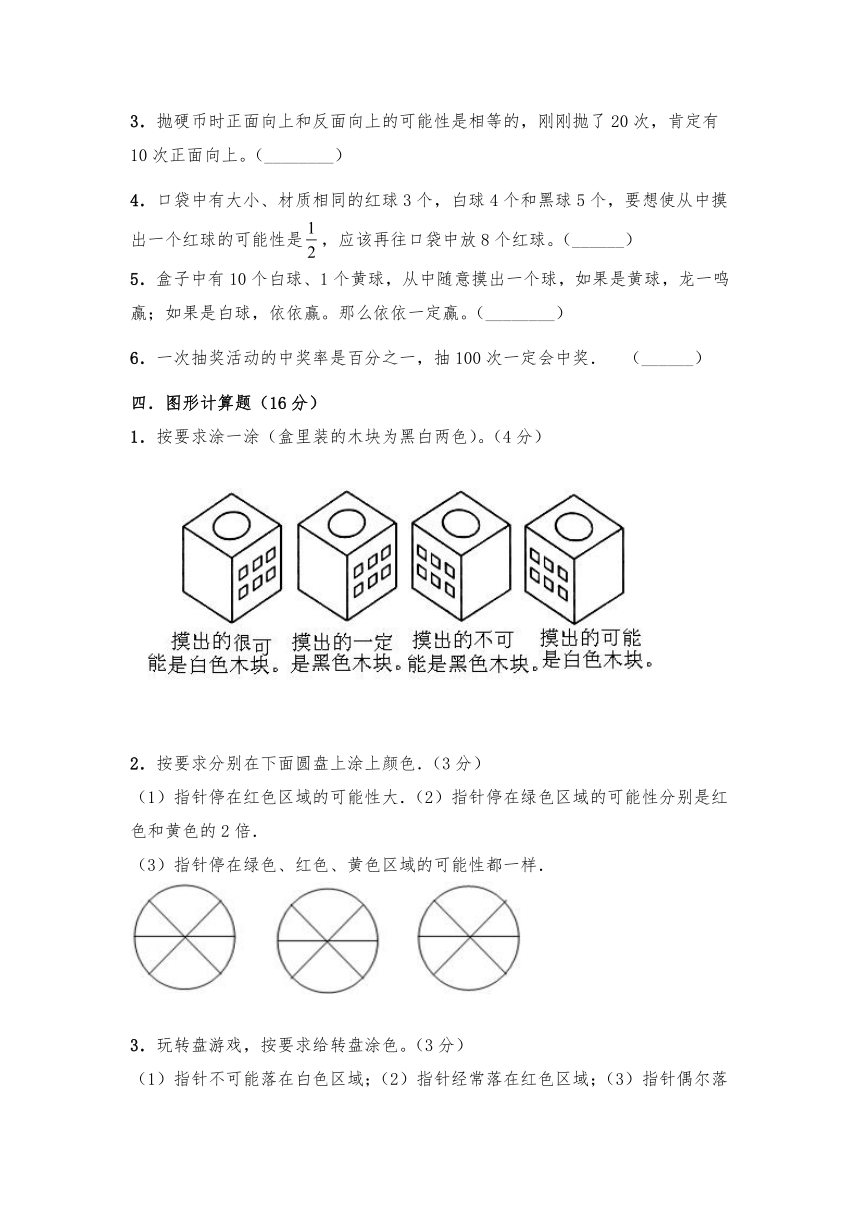
1.按要求涂一涂(盒里装的木块为黑白两色)。(4分)
2.按要求分别在下面圆盘上涂上颜色.(3分)
(1)指针停在红色区域的可能性大.(2)指针停在绿色区域的可能性分别是红色和黄色的2倍.
(3)指针停在绿色、红色、黄色区域的可能性都一样.
3.玩转盘游戏,按要求给转盘涂色。(3分)
(1)指针不可能落在白色区域;(2)指针经常落在红色区域;(3)指针偶尔落在黑色区域;
(4)指针落在黄色和绿色区域的可能性相等。
4.(把10张卡片反扣在桌面上,每张卡片上写有0~9中的某一个数字。任意翻开一张,要使得到数字“6”的可能性最大,得到数字“9”的可能性最小,不可能得到数字“0”,卡片上可以填哪些数字?请你填一填。(3分)
5.把10张字母卡片放入纸袋,随意摸一张,要使摸出字母“”的可能性最大,字母“”的可能性最小,卡片上可以是什么字母?(3分)
五、应用题(每题7分,共42分)
1.一个仅装有球的不透明布袋里共有5个球(只有编号不同),编号分别为1,2,3,4,5.从中任意摸出一个球,记下编号后放回,搅匀,再任意摸出一个球,两次摸出的球的编号之和为奇数的可能性超吗?请说明理由。
2.看图回答.
(1)从袋子里摸一个球,会有几种可能的情况?
(2)摸到红色球的可能性是几分之几?
(3)摸到各种颜色球的可能性相等吗?
(4)要想增加摸到红色球的可能性,可以怎样做?
(5)怎样做就能一定摸到红色球?
3.某商人设计了一个如下图所示的转盘游戏。游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母,则收费2元;若指针指向字母则奖3元;若指针指向字母,则奖1元。一天,前来玩游戏的人共转动转盘800次。你认为商人盈利的可能性大还是亏损的可能性大?
4.乐乐与文文用这8张扑克牌做游戏。
乐乐:每次摸一张牌,摸到的牌上的数小于5是我赢,大于5是你赢。文文:如果这个游戏公平,我就跟你玩。这个游戏规则公平吗?为什么?如果不公平,谁赢的可能性大?怎样修改就公平了呢?(说明:“”代表“1”)
5.一共有18名同学做击鼓传花的游戏,其中男、女生各9名。鼓声停,花在女生手里就由女生组表演节目,花在男生手里就由男生组表演节目。这个游戏公平吗?
6.纸牌游戏.
小丽和小红喜欢用扑克牌设计各类智力游戏活动。
(1)小丽用上图中的5张牌,让小红任意抽取2张,如果两张的点数和是3的倍数,则获胜。小红获胜的可能性是(
)。把推算的过程记录在方框里。
(2)小丽和小红各抓了以下三张牌(如左下图),通过两两大小比较的方法获胜(三局两胜制)。小红怎样出牌才能获胜?把小红出牌的策略记录在右下图的方框里。
(3)小红和小丽用空白的纸牌自制一幅新式的纸牌,其前5张的点数如下图:
按这个设计规律,则第张纸牌上的点数是(
)点;前张纸牌上的总点数是(
)点。
把你的想法记录在方框内:
答案
一、选择题
1.A2.B3.D4.B5.A6.A7.B8.D9.C
10.B11.C12.B13.B14.A15.A16.B
二、填空题
1.
2.
3.红
4
4.4
5.唱歌
6.
10
7.黄
1
白
8.3
1
9.8或9
10.圆
三、判断题
1.×2.√3.×4.×5.×6.×
四.图形计算题
1.第一个盒子里放白色多于其它颜色木块,摸出的很可能是白色木块;第二个盒子里全放黑色木块,摸出的一定是黑色木块;第三个盒子里不放黑色木块,摸出的不可能是黑色木块;第四个盒子里放白色和其它颜色木块,摸出的可能是白色木块。
。
(涂法不唯一。)
2.
3.(涂法不唯一)
4.由“数字“6”的可能性最大,得到数字“9”的可能性最小”说明6的张数最多,9的张数最少;不可能得到数字“0”说明没有0。所以卡片可以填:1、1、3、3、6、6、6、6、6、9。(答案不唯一)
5.根据分析可得,此题答案不唯一,合理即可。如:
五、应用题
1.两次摸出的球的编号之和为奇数的情况有12种:
两次摸出的两个球是1和2或2和1;两次摸出的两个球是1和4或4和1;
两次摸出的两个球是2和3或3和2;两次摸出的两个球是4和3或3和4;
两次摸出的两个球是4和5或5和4;两次摸出的两个球是2和5或5和2;
摸出的两个球共有5×5=25种情况,12÷25=48
%48
%<50
%
所以两次摸出的球的编号之和为奇数的可能性不超。
2.(1)解:从袋子里摸一个球,会有4种可能的情况.
(2)解:摸到红色球的可能性是四分之一.
(3)解:摸到各种颜色球的可能性是相等.
(4)解:要想增加摸到红色球的可能性:可以增加一个红球,减少一个其他颜色的球
(5)解:当四个球都是红色的,就能一定摸到红色球.
3.指针指向字母的次数约为(次)
指针指向字母的次数约为(次)
指针指向字母的次数约为(次)
(元)
(元)
(元)
(元)
答:我认为商人盈利的可能性大。
4.这个游戏规则不公平。因为小于5的有4张,大于5的有3张,所以这个游戏规则不公平,乐乐赢的可能性大。
修改:每次摸一张牌,摸到的牌上的数小于5是乐乐赢,大于或等于5是文文赢。(方法不唯一)
5.方法一:因为一共有18名同学,花落到每个人手里的可能性都是,男生有9名,女生有9名,男生组和女生组表演节目的可能性都是,这个游戏公平。
方法二:18名同学中男、女生各9名,可以认为是两个组,即男生为一组,女生为一组,花落到男生组和落到女生组的可能性都是,这个游戏公平。
6.(1)小红抽到的情况如下:,,,,,,,,,,其中两张点数和是3的倍数情况如下:,,,,所以小红获胜的可能性是。
(2)小丽:5,7,9,小红:6,8,2
(3)
(前个偶数和为,前个数和为,则前个奇数和为)
一、选择题(每题1分,共16分)
1.张阳给姑姑打电话.他只记得姑姑的电话号码是“862
6538”,他准确拨出电话的可能性是(?
)
A.
B.
C.
D.
2.投掷3次硬币,有2次正面朝上,1次反面朝上,那么,投掷第4次硬币正面朝上的可能性是(
)
A.
B.
C.
D.
3.在袋子里放4个黄球和1个白球(两种球除了颜色不同其余都相同),从中任意摸出一个球,下列说法正确的是(
)。
A.一定能摸到黄球
B.不可能摸到白球
C.摸到黄球和白球的可能性相等
D.摸到每个球的可能性相等
4.一个仅装有球的不透明布袋里共有4个红球,5个黑球和7个黄球,从中任意摸出一个球,摸到(
)的可能性最大。
A.红球
B.黄球
C.黑球
D.无法确定
5.用下面转盘做游戏,指针停在1号区域的可能性比停在4号区域的可能性(
)。
A.大
B.小
C.相等
D.不确定
6.从、、、四张卡片中任选两张组成一个两位数,组成的两位数中可能性最大的是(
)。
A.合数
B.质数
C.偶数
D.奇数
7.一个袋中装有一双红袜子和一双蓝袜子,任意摸出两只,能配成颜色相同的一双袜子的可能性是(
)。
A.
B.
C.
D.
8.小明任意买一张电影票,这张票的座位号在下列情况中可能性最小的是(
)。
A.座位号是偶数
B.座位号是2,22或222
C.座位号是10的倍数
D.座位号是10
9.小强把1—9的数字卡片共九张打乱顺序反扣在桌上,从中任意摸一张,摸到质数的可能性与摸到合数的可能性相比(
)。
A.摸到质数的可能性大
B.摸到合数的可能性大
C.摸到质数与摸到合数的可能性相等
D.无法确定
10.甲、乙两人做掷骰子游戏,骰子的六个面上分别标有1、2、3、4、5、6,下面(
)游戏规则是公平的。
A.质数甲贏,合数乙贏。
B.奇数甲贏,偶数乙贏。
C.小于3的甲贏,大于3的乙贏。
D.小于4的甲贏,大于4的乙贏。
11.如图,向标靶随意投一支飞标,如果投出的飞标都中靶,且投中每个方格的机会均等,那么投中涂色部分的可能性是(
)。
A.
B.
C.
12.有一种游戏的规则是:先旋转转盘的指针,如果指针箭头停在3的倍数的位置,就可以从盒子里摸出一个珠子。如果摸到黑色珠子就能得到奖品,东东玩了一次,他旋转转盘后,指针箭头所在位置和盒子里珠子的情况如下图所示。下面说法合理的是(
)。
A.他不可能得到奖品
B.他得到奖品的可能性小
C.他得到奖品的可能性大D.他一定可以得到奖品
13.小华和小敏玩掷骰子游戏,一起掷两个骰子,得到两个数,和是6小华得一分,和是12小敏得一分,和是其它数两人都不得分。掷20次,得分高的人获胜。这个游戏规则(
)。
A.公平,两人赢的可能性一样大
B.不公平,小华赢的可能性更大
C.不公平,小敏赢的可能性更大
D.无法确定
14.盒子里有8个球,球上分别标有2、3、4、5、6、7、8、9,优优和小贤两人玩摸球游戏,下面的规则中对双方都公平的是(
)。
A.任意摸一球,摸到质数优优胜,摸到合数小贤胜
B.任意摸一球,摸到的数小于5优优胜,摸到的数大于5小贤胜
C.任意摸一球,摸到2的倍数优优胜,摸到3的倍数小贤胜
D.任意摸一球,摸到4的因数优优胜,摸到5的因数小贤胜
15.任意抛掷两枚一元硬币,出现一正一反的机会是(
)。
A.
B.
C.
D.1
16.下列说法正确的是(????
)
A.彩票中奖的机会是1%,买100张一定能中奖.
B.从1、2、3、4、5这五个数字中任取一个数,取得奇数的可能性大.
C.可能性很小的事情在一次实验中一定不会发生.
D.一枚硬币,小明抛掷5次有4次正面向上,则抛掷一枚硬币正面向上的概率为0.8.
二、填空题(每题2分,共20分)
1.一个正方体,它的1个面上写着“1”,2个面上写着“2”,3个面上写着“3”,抛起这个正方体落下后,朝上的数是奇数的可能性是____。
2.要从甲、乙、丙、丁4人中抽签选出两人参加素质检测,恰好抽到甲、乙两人的可能性是(________)。
3.一个袋子里有2个黑球、4个红球和1个白球,任意摸一个球,摸到(________)球的可能性最大。要想保证摸到的一定是红球,至少需要摸出(________)个。
4.如图,任摸一个球,要使摸到黄球的可能性比白球大,盒子中至少应增加(________)个黄球。
5.新年联欢会用抽签决定表演的节目,抽签盒里有8张唱歌、5张朗诵、3张跳舞。小明任意抽一张,抽到(________)的可能性最大。
6.掷一个骰子,单数朝上的可能性是________,双数朝上的可能性是________。如果掷60次,“6”朝上的次数大约是________。
7.口袋里有1个白球和2个黄球,每个球除颜色外都相同,任意摸出一个球,摸到(______)球的可能性大,如果要使摸到两种球的可能性相等,那么需要再往口袋里放入(______)个(______)球。
8.王东和李阳用转盘(如图)玩游戏,转盘指针指向质数就是王东胜,指向合数就是李阳胜。在A、B处填上合适的数(不与转盘上的数相同),使这个游戏对双方都公平。A可以是(______),B可以是(______)。
9.在一个不透明的布袋中,装有白色小球10个、红色小球7个和若干个黑色小球,这些小球除颜色外其余都相同。要从布袋中随机摸出1个小球,若摸出的小球是黑色的可能性大于红色的可能性且小于白色的可能性,则布袋中的黑色小球可以有(______)个。
10.如图所示,分别向周长相等的圆和正方形内扔同样大小的石子儿,命中(________)形的可能性更大。
三、判断题(每题1分,共6分)
1.明天一定会下雨.(____)
2.一个袋子里装了形状、大小都相同的3个绿球和3个黄球,每次摸到1个球,摸到绿球和黄球的可能性大小是一样的。(________)
3.抛硬币时正面向上和反面向上的可能性是相等的,刚刚抛了20次,肯定有10次正面向上。(________)
4.口袋中有大小、材质相同的红球3个,白球4个和黑球5个,要想使从中摸出一个红球的可能性是,应该再往口袋中放8个红球。(______)
5.盒子中有10个白球、1个黄球,从中随意摸出一个球,如果是黄球,龙一鸣赢;如果是白球,依依赢。那么依依一定赢。(________)
6.一次抽奖活动的中奖率是百分之一,抽100次一定会中奖.
(______)
四.图形计算题(16分)
1.按要求涂一涂(盒里装的木块为黑白两色)。(4分)
2.按要求分别在下面圆盘上涂上颜色.(3分)
(1)指针停在红色区域的可能性大.(2)指针停在绿色区域的可能性分别是红色和黄色的2倍.
(3)指针停在绿色、红色、黄色区域的可能性都一样.
3.玩转盘游戏,按要求给转盘涂色。(3分)
(1)指针不可能落在白色区域;(2)指针经常落在红色区域;(3)指针偶尔落在黑色区域;
(4)指针落在黄色和绿色区域的可能性相等。
4.(把10张卡片反扣在桌面上,每张卡片上写有0~9中的某一个数字。任意翻开一张,要使得到数字“6”的可能性最大,得到数字“9”的可能性最小,不可能得到数字“0”,卡片上可以填哪些数字?请你填一填。(3分)
5.把10张字母卡片放入纸袋,随意摸一张,要使摸出字母“”的可能性最大,字母“”的可能性最小,卡片上可以是什么字母?(3分)
五、应用题(每题7分,共42分)
1.一个仅装有球的不透明布袋里共有5个球(只有编号不同),编号分别为1,2,3,4,5.从中任意摸出一个球,记下编号后放回,搅匀,再任意摸出一个球,两次摸出的球的编号之和为奇数的可能性超吗?请说明理由。
2.看图回答.
(1)从袋子里摸一个球,会有几种可能的情况?
(2)摸到红色球的可能性是几分之几?
(3)摸到各种颜色球的可能性相等吗?
(4)要想增加摸到红色球的可能性,可以怎样做?
(5)怎样做就能一定摸到红色球?
3.某商人设计了一个如下图所示的转盘游戏。游戏规定:参与者自由转动转盘,转盘停止后,若指针指向字母,则收费2元;若指针指向字母则奖3元;若指针指向字母,则奖1元。一天,前来玩游戏的人共转动转盘800次。你认为商人盈利的可能性大还是亏损的可能性大?
4.乐乐与文文用这8张扑克牌做游戏。
乐乐:每次摸一张牌,摸到的牌上的数小于5是我赢,大于5是你赢。文文:如果这个游戏公平,我就跟你玩。这个游戏规则公平吗?为什么?如果不公平,谁赢的可能性大?怎样修改就公平了呢?(说明:“”代表“1”)
5.一共有18名同学做击鼓传花的游戏,其中男、女生各9名。鼓声停,花在女生手里就由女生组表演节目,花在男生手里就由男生组表演节目。这个游戏公平吗?
6.纸牌游戏.
小丽和小红喜欢用扑克牌设计各类智力游戏活动。
(1)小丽用上图中的5张牌,让小红任意抽取2张,如果两张的点数和是3的倍数,则获胜。小红获胜的可能性是(
)。把推算的过程记录在方框里。
(2)小丽和小红各抓了以下三张牌(如左下图),通过两两大小比较的方法获胜(三局两胜制)。小红怎样出牌才能获胜?把小红出牌的策略记录在右下图的方框里。
(3)小红和小丽用空白的纸牌自制一幅新式的纸牌,其前5张的点数如下图:
按这个设计规律,则第张纸牌上的点数是(
)点;前张纸牌上的总点数是(
)点。
把你的想法记录在方框内:
答案
一、选择题
1.A2.B3.D4.B5.A6.A7.B8.D9.C
10.B11.C12.B13.B14.A15.A16.B
二、填空题
1.
2.
3.红
4
4.4
5.唱歌
6.
10
7.黄
1
白
8.3
1
9.8或9
10.圆
三、判断题
1.×2.√3.×4.×5.×6.×
四.图形计算题
1.第一个盒子里放白色多于其它颜色木块,摸出的很可能是白色木块;第二个盒子里全放黑色木块,摸出的一定是黑色木块;第三个盒子里不放黑色木块,摸出的不可能是黑色木块;第四个盒子里放白色和其它颜色木块,摸出的可能是白色木块。
。
(涂法不唯一。)
2.
3.(涂法不唯一)
4.由“数字“6”的可能性最大,得到数字“9”的可能性最小”说明6的张数最多,9的张数最少;不可能得到数字“0”说明没有0。所以卡片可以填:1、1、3、3、6、6、6、6、6、9。(答案不唯一)
5.根据分析可得,此题答案不唯一,合理即可。如:
五、应用题
1.两次摸出的球的编号之和为奇数的情况有12种:
两次摸出的两个球是1和2或2和1;两次摸出的两个球是1和4或4和1;
两次摸出的两个球是2和3或3和2;两次摸出的两个球是4和3或3和4;
两次摸出的两个球是4和5或5和4;两次摸出的两个球是2和5或5和2;
摸出的两个球共有5×5=25种情况,12÷25=48
%48
%<50
%
所以两次摸出的球的编号之和为奇数的可能性不超。
2.(1)解:从袋子里摸一个球,会有4种可能的情况.
(2)解:摸到红色球的可能性是四分之一.
(3)解:摸到各种颜色球的可能性是相等.
(4)解:要想增加摸到红色球的可能性:可以增加一个红球,减少一个其他颜色的球
(5)解:当四个球都是红色的,就能一定摸到红色球.
3.指针指向字母的次数约为(次)
指针指向字母的次数约为(次)
指针指向字母的次数约为(次)
(元)
(元)
(元)
(元)
答:我认为商人盈利的可能性大。
4.这个游戏规则不公平。因为小于5的有4张,大于5的有3张,所以这个游戏规则不公平,乐乐赢的可能性大。
修改:每次摸一张牌,摸到的牌上的数小于5是乐乐赢,大于或等于5是文文赢。(方法不唯一)
5.方法一:因为一共有18名同学,花落到每个人手里的可能性都是,男生有9名,女生有9名,男生组和女生组表演节目的可能性都是,这个游戏公平。
方法二:18名同学中男、女生各9名,可以认为是两个组,即男生为一组,女生为一组,花落到男生组和落到女生组的可能性都是,这个游戏公平。
6.(1)小红抽到的情况如下:,,,,,,,,,,其中两张点数和是3的倍数情况如下:,,,,所以小红获胜的可能性是。
(2)小丽:5,7,9,小红:6,8,2
(3)
(前个偶数和为,前个数和为,则前个奇数和为)
