六年级数学下册试题 一课一练《图形与几何--图形的拼组与图形变换》 人教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《图形与几何--图形的拼组与图形变换》 人教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 688.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 13:56:40 | ||
图片预览



文档简介
《图形与几何--图形的拼组与图形变换》
一、选择题(每题1分,共16分)
1.一个长、宽都是4厘米,高12厘米的长方体截成三个一样大小的正方体,表面积增加了(
)平方厘米。
A.16
B.32
C.48
D.64
2.最少(
)个小正方体可以拼出一个大正方体。
A.4
B.6
C.8
3.一个长方体刚好切成3个相同的正方体,表面积增加了36dm2,原来长方体的体积是(
)dm3。
A.108
B.81
C.432
D.648
4.把两个棱长为3厘米的正方体木块和一个长12厘米,宽6厘米,高6厘米的长方体木块粘贴在一起(如图),那么粘贴后的表面积比原来三个木块表面积之和减少(
)。
A.54平方厘米
B.36平方厘米
C.27平方厘米
D.18平方厘米
5.一个长方体盒子,从里面量,长6分米,宽5分米,高4分米。如果把棱长2分米的积木装进盒子,并使积木不外露,最多可以装(
)块。
A.6
B.10
C.12
D.15
6.把一个圆平均分成16份,然后剪拼成一个近似的长方形,转化后的长方形与圆相比,(
)。
A.周长和面积都没变
B.周长和面积都变了
C.周长没变,面积变了
D.周长变了,面积不变
7.把一张平行四边形卡片剪一刀分成两个图形,下面几种情况中不可能出现的是(
)。
A.两个三角形
B.两个平行四边形
C.两个梯形
D.一个平行四边形与一个梯形
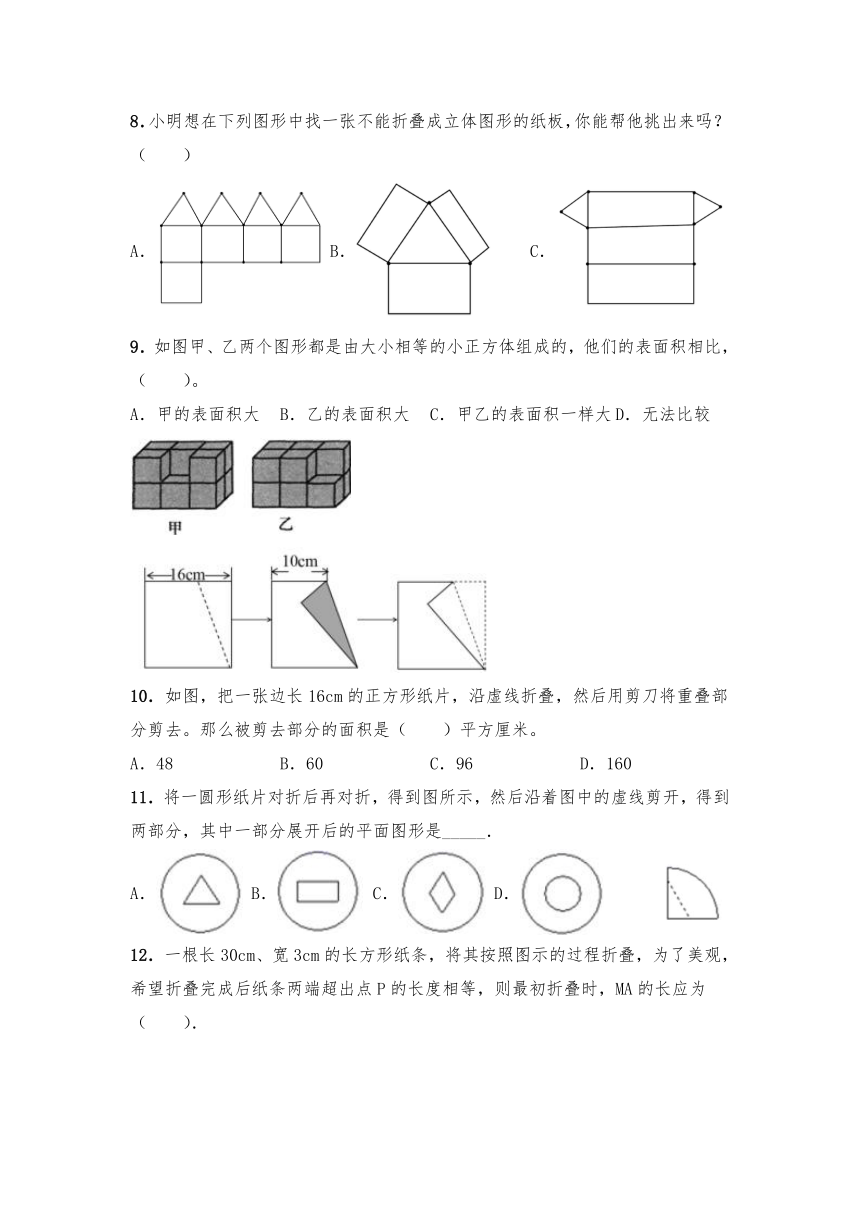
8.小明想在下列图形中找一张不能折叠成立体图形的纸板,你能帮他挑出来吗?(
)
A.
B.
C.
9.如图甲、乙两个图形都是由大小相等的小正方体组成的,他们的表面积相比,(
)。
A.甲的表面积大
B.乙的表面积大
C.甲乙的表面积一样大
D.无法比较
10.如图,把一张边长16cm的正方形纸片,沿虚线折叠,然后用剪刀将重叠部分剪去。那么被剪去部分的面积是(
)平方厘米。
A.48
B.60
C.96
D.160
11.将一圆形纸片对折后再对折,得到图所示,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是_____.
A.
B.
C.
D.
12.一根长30cm、宽3cm的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后纸条两端超出点P的长度相等,则最初折叠时,MA的长应为(
).
A.7.5cm
B.9cm
C.12cm
D.10.
5cm
13.将厚0.1毫米的一张纸对折,再对折……这样对折5次后,纸的厚度将达到(
)。
A.3.2毫米
B.6.4毫米
C.1.6毫米
14.下面每组中的两个图形经过平移后,可以互相重合的是(
)。
A.
B.
C.
15.由图形(1)不能变为图形(2)的方法是(
)。
A.图形(1)绕“O”点逆时针方向旋转90°得到图形(2)
B.图形(1)绕“O”点顺时针方向旋转90°得到图形(2)
C.图形(1)绕“O”点逆时针方向旋转270°得到图形(2)
D.以线段OP所在的直线为对称轴画图形(1)的轴对称图形得到图形(2)
16.将一个圆锥沿着它的高平均切成两块,切面一定是一个(
)。
A.长方形
B.圆形
C.扇形
D.等腰三角形
二、填空题(每题2分,共20分)
1.在长25厘米,宽20厘米,高10厘米的长方体的八个角上,剪去棱长为5厘米的正方体,求剩下部分的体积是(______)。
2.一根圆柱体木料长4.5米,把它平均分成5个小的圆柱体,表面积增加了160平方厘米,每个小圆柱体的体积是(________)立方分米。
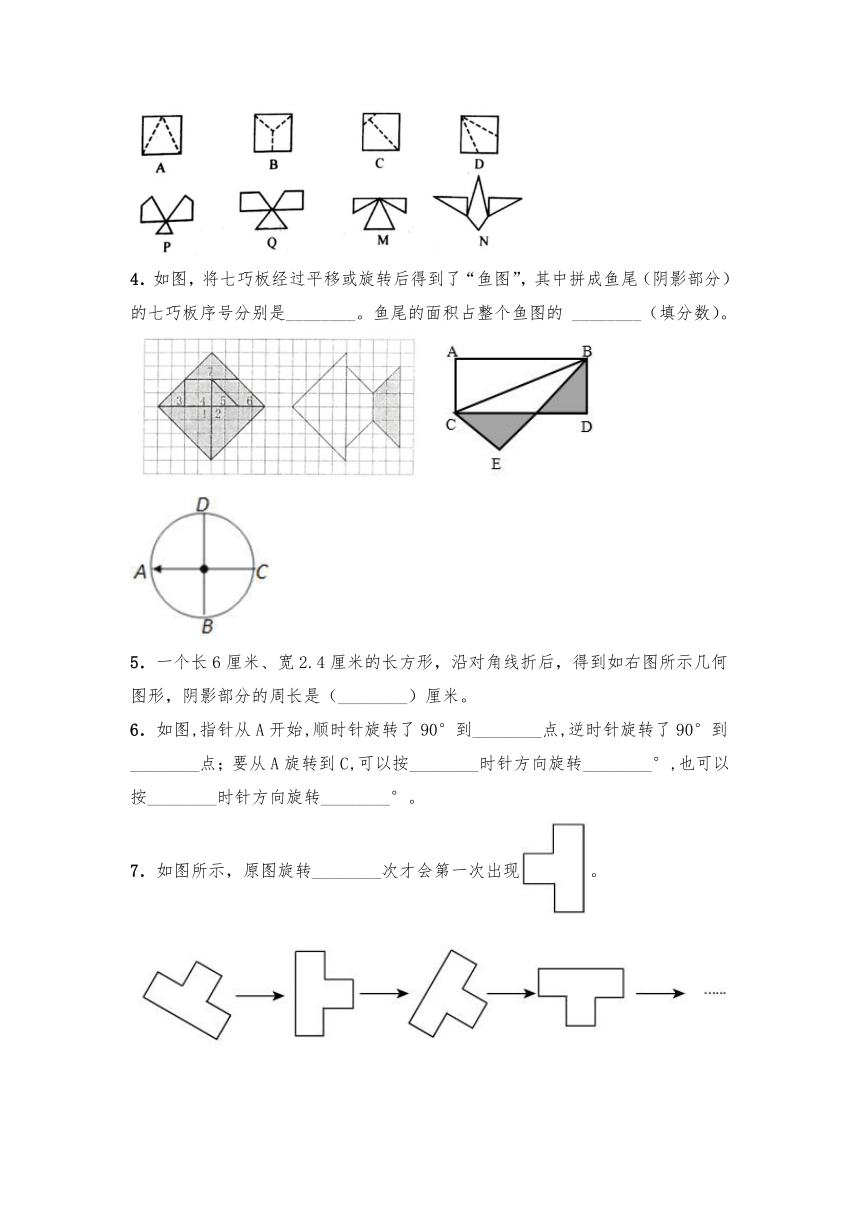
3.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后得到标号为P,Q,M,N的四组图形,试按照“哪个正方形剪开后得到哪组图形”的对应关系填空:A与________对应;B与________对应;C与________对应;D与________对应.
4.如图,将七巧板经过平移或旋转后得到了“鱼图”,其中拼成鱼尾(阴影部分)的七巧板序号分别是________。鱼尾的面积占整个鱼图的
________(填分数)。
5.一个长6厘米、宽2.4厘米的长方形,沿对角线折后,得到如右图所示几何图形,阴影部分的周长是(________)厘米。
6.如图,指针从A开始,顺时针旋转了90°到________点,逆时针旋转了90°到________点;要从A旋转到C,可以按________时针方向旋转________°,也可以按________时针方向旋转________°。
7.如图所示,原图旋转________次才会第一次出现。
8.观察下图,图①和图②中的三角形均为等边三角形,图①中小三角形的面积是大三角形面积的。图③中小正方形的面积占大正方形面积的。
9.小明买了一块长方体蛋糕,和同行的伙伴分享,他决定从下面分别截去高为3cm、2cm的长方体后,给自己留下一个正方体,(如图,单位:cm),结果表面积减少了120cm2,那么原来长方体蛋糕的体积是(________)cm3。
10.在下图中,有两个完全相同的等腰直角三角形。已知左下图中正方形的面积是40cm2,则右下图中正方形的面积是(______)cm2。
三、判断题(每题1分,共6分)
1.两个面积相等的梯形一定能拼成一个平行四边形。(______)
2.两个三角形一定可以拼成一个平行四边形。(________)
3.把一张正方形的纸连续对折4次,折后的每一小块占这张正方形纸的。(________)
4.从10:00到10:40分针旋转了。(________)
5.
左图是一个轴对称图形。(________)
6.平移、旋转和轴对称不改变图形的形状和大小。(________)
四、图形计算题(28分)
1.画一条线段,把下面的梯形分成面积相等的两部分。请画出两种不同的分法。(4分)
2.把下面图形分成我们学过的图形,你有几种方法?(单位:厘米)
(3分)
(先填写上面的图形,再填写下面的图形)
3.在上底为4厘米,下底为6厘米的梯形中画一条线段,把梯形分成面积相等的两部分。(画出三种分法)(3分)
4.有一块豆腐,请你看看怎样切3刀把它切成8块,把它画下来.(4分)
5.将图分成两块,然后拼成一个正方形。(直接铅笔画图)(4分)
6.你会根据对称轴画出另外一半吗?
(2分)
7.把一个大正方形分成9个相同的小方格,给图中的1个白色小方格画上斜线,使画斜线的部分成为一个轴对称图形。请用4种不同的画法表示。(4分)
8.在的方格纸中,用格点连线将方格纸分割成大小形状都相同的两部分。如图所示就是其中的二例。根据题意另外再给出3种分割方法,在下图中画出。(4分)
五、应用题(每题6分,共30分)
1.把一个长方体的高缩短后,它就变成了一个正方体,表面积比原来减少了,原来长方体的表面积是多少平方厘米?
2.足球是用黑、白两种颜色的皮缝制而成的,黑皮是正五边形,白皮是正六边形,其中黑皮有12块,白皮有多少块?
3.把高20厘米的圆柱按下图切开,拼成近似的长方体,表面积增加了120平方厘米。这圆柱的体积是多少立方厘米?
4.探索与发现.
(1)下图中每个小长方形的长都是6cm,宽都是4cm,5个这样的小长方形按照如图方式摆放成一个大长方形.这个大长方形的周长是(
)cm.如果给你5个长2cm、宽1cm的小长方形,你能把它们按照这种方式摆出一个大长方形吗?如果能,请你画出示意图;如果不能,请你说明理由.
(2)小宇用5个小长方形按照第(1)题中的方式摆出了一个更大的长方形.他所用的小长方形的长、宽可能是多少?请你写出2种,填在下表中.
长/cm
宽/cm
根据上面的探索,我发现所用的小长方形的长和宽之间有这样的规律:
。
5.有一个长方体,如图,(单位:厘米)现将它“切成”完全一样的三个长方体.(1)共有
种切法.(2)怎样切,使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,算一算表面积最多增加了多少?
答案
一、选择题
1.D2.C3.B4.A5.C6.D7.D
8.B
9.A10.A11.C12.D13.A14.B15.A16.D
二、填空题
1.4500立方厘米
2.1.8
3.M
Q
P
N
4.3、4、5或6、7
5.16.8
6.D
B
顺
180
逆
180
7.5
8.;
9.396
10.45
三、判断题
1.×2.×3.√4.×5.√6.√
四.图形计算题
1.
2.
(长方)形+(梯)形
(长方)形+(三角)形
(梯)形+(三角)形
3.画图如下:
4.切3刀如图:
.
【详解】把这块豆腐分成8小块,最少要切三刀,即纵切两刀,横切一刀.纵切一刀时,即可切成2小块,再纵切一刀,要与第一次的切缝交叉,这样就分成4块,再横切一刀,即可把分成的这4小块再一分为二,就是8小块.
5.
6.
7.
如图所示:
8.作图如下:
(答案不唯一)
五、应用题
1.
答:原来长方体的表面积是210平方厘米。
2.所有的黑皮的边数:12×5=60,一块白皮的边数是6,则白皮的数量为:
60×2÷6=120÷6=20(块)
答:白皮有20块。
3.底面半径:120÷20÷2=3(厘米)
体积:3.14×32×20=565.2(立方厘米)
答:这圆柱的体积是565.2立方厘米。
4.(1)44;不能,因为:按着这种方式摆长方形的长一边是2+2=4(cm),另一边是1+1+1=3(cm),一个长方形的两个长不相等,所以不能.
(2)
长/cm
12
18
宽/cm
8
12
小长方形的长和宽之间有这样的规律:长:宽=3:2
5.(1)有三种切法,
①24÷3=8,可以切长为12、宽为8、高为6的三个长方体;
②12÷3=4,可以切成长为24宽为4高为6的三个长方体;
③6÷3=2可以切成长为24宽为12高为2的三个长方体.故答案为3.
(2)第三种切法使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,
增加的是长为24宽为12的四个面的面积:24×12×4=1152.
答:表面积增加了1152平方厘米.
一、选择题(每题1分,共16分)
1.一个长、宽都是4厘米,高12厘米的长方体截成三个一样大小的正方体,表面积增加了(
)平方厘米。
A.16
B.32
C.48
D.64
2.最少(
)个小正方体可以拼出一个大正方体。
A.4
B.6
C.8
3.一个长方体刚好切成3个相同的正方体,表面积增加了36dm2,原来长方体的体积是(
)dm3。
A.108
B.81
C.432
D.648
4.把两个棱长为3厘米的正方体木块和一个长12厘米,宽6厘米,高6厘米的长方体木块粘贴在一起(如图),那么粘贴后的表面积比原来三个木块表面积之和减少(
)。
A.54平方厘米
B.36平方厘米
C.27平方厘米
D.18平方厘米
5.一个长方体盒子,从里面量,长6分米,宽5分米,高4分米。如果把棱长2分米的积木装进盒子,并使积木不外露,最多可以装(
)块。
A.6
B.10
C.12
D.15
6.把一个圆平均分成16份,然后剪拼成一个近似的长方形,转化后的长方形与圆相比,(
)。
A.周长和面积都没变
B.周长和面积都变了
C.周长没变,面积变了
D.周长变了,面积不变
7.把一张平行四边形卡片剪一刀分成两个图形,下面几种情况中不可能出现的是(
)。
A.两个三角形
B.两个平行四边形
C.两个梯形
D.一个平行四边形与一个梯形
8.小明想在下列图形中找一张不能折叠成立体图形的纸板,你能帮他挑出来吗?(
)
A.
B.
C.
9.如图甲、乙两个图形都是由大小相等的小正方体组成的,他们的表面积相比,(
)。
A.甲的表面积大
B.乙的表面积大
C.甲乙的表面积一样大
D.无法比较
10.如图,把一张边长16cm的正方形纸片,沿虚线折叠,然后用剪刀将重叠部分剪去。那么被剪去部分的面积是(
)平方厘米。
A.48
B.60
C.96
D.160
11.将一圆形纸片对折后再对折,得到图所示,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是_____.
A.
B.
C.
D.
12.一根长30cm、宽3cm的长方形纸条,将其按照图示的过程折叠,为了美观,希望折叠完成后纸条两端超出点P的长度相等,则最初折叠时,MA的长应为(
).
A.7.5cm
B.9cm
C.12cm
D.10.
5cm
13.将厚0.1毫米的一张纸对折,再对折……这样对折5次后,纸的厚度将达到(
)。
A.3.2毫米
B.6.4毫米
C.1.6毫米
14.下面每组中的两个图形经过平移后,可以互相重合的是(
)。
A.
B.
C.
15.由图形(1)不能变为图形(2)的方法是(
)。
A.图形(1)绕“O”点逆时针方向旋转90°得到图形(2)
B.图形(1)绕“O”点顺时针方向旋转90°得到图形(2)
C.图形(1)绕“O”点逆时针方向旋转270°得到图形(2)
D.以线段OP所在的直线为对称轴画图形(1)的轴对称图形得到图形(2)
16.将一个圆锥沿着它的高平均切成两块,切面一定是一个(
)。
A.长方形
B.圆形
C.扇形
D.等腰三角形
二、填空题(每题2分,共20分)
1.在长25厘米,宽20厘米,高10厘米的长方体的八个角上,剪去棱长为5厘米的正方体,求剩下部分的体积是(______)。
2.一根圆柱体木料长4.5米,把它平均分成5个小的圆柱体,表面积增加了160平方厘米,每个小圆柱体的体积是(________)立方分米。
3.如图,将标号为A,B,C,D的正方形沿图中的虚线剪开后得到标号为P,Q,M,N的四组图形,试按照“哪个正方形剪开后得到哪组图形”的对应关系填空:A与________对应;B与________对应;C与________对应;D与________对应.
4.如图,将七巧板经过平移或旋转后得到了“鱼图”,其中拼成鱼尾(阴影部分)的七巧板序号分别是________。鱼尾的面积占整个鱼图的
________(填分数)。
5.一个长6厘米、宽2.4厘米的长方形,沿对角线折后,得到如右图所示几何图形,阴影部分的周长是(________)厘米。
6.如图,指针从A开始,顺时针旋转了90°到________点,逆时针旋转了90°到________点;要从A旋转到C,可以按________时针方向旋转________°,也可以按________时针方向旋转________°。
7.如图所示,原图旋转________次才会第一次出现。
8.观察下图,图①和图②中的三角形均为等边三角形,图①中小三角形的面积是大三角形面积的。图③中小正方形的面积占大正方形面积的。
9.小明买了一块长方体蛋糕,和同行的伙伴分享,他决定从下面分别截去高为3cm、2cm的长方体后,给自己留下一个正方体,(如图,单位:cm),结果表面积减少了120cm2,那么原来长方体蛋糕的体积是(________)cm3。
10.在下图中,有两个完全相同的等腰直角三角形。已知左下图中正方形的面积是40cm2,则右下图中正方形的面积是(______)cm2。
三、判断题(每题1分,共6分)
1.两个面积相等的梯形一定能拼成一个平行四边形。(______)
2.两个三角形一定可以拼成一个平行四边形。(________)
3.把一张正方形的纸连续对折4次,折后的每一小块占这张正方形纸的。(________)
4.从10:00到10:40分针旋转了。(________)
5.
左图是一个轴对称图形。(________)
6.平移、旋转和轴对称不改变图形的形状和大小。(________)
四、图形计算题(28分)
1.画一条线段,把下面的梯形分成面积相等的两部分。请画出两种不同的分法。(4分)
2.把下面图形分成我们学过的图形,你有几种方法?(单位:厘米)
(3分)
(先填写上面的图形,再填写下面的图形)
3.在上底为4厘米,下底为6厘米的梯形中画一条线段,把梯形分成面积相等的两部分。(画出三种分法)(3分)
4.有一块豆腐,请你看看怎样切3刀把它切成8块,把它画下来.(4分)
5.将图分成两块,然后拼成一个正方形。(直接铅笔画图)(4分)
6.你会根据对称轴画出另外一半吗?
(2分)
7.把一个大正方形分成9个相同的小方格,给图中的1个白色小方格画上斜线,使画斜线的部分成为一个轴对称图形。请用4种不同的画法表示。(4分)
8.在的方格纸中,用格点连线将方格纸分割成大小形状都相同的两部分。如图所示就是其中的二例。根据题意另外再给出3种分割方法,在下图中画出。(4分)
五、应用题(每题6分,共30分)
1.把一个长方体的高缩短后,它就变成了一个正方体,表面积比原来减少了,原来长方体的表面积是多少平方厘米?
2.足球是用黑、白两种颜色的皮缝制而成的,黑皮是正五边形,白皮是正六边形,其中黑皮有12块,白皮有多少块?
3.把高20厘米的圆柱按下图切开,拼成近似的长方体,表面积增加了120平方厘米。这圆柱的体积是多少立方厘米?
4.探索与发现.
(1)下图中每个小长方形的长都是6cm,宽都是4cm,5个这样的小长方形按照如图方式摆放成一个大长方形.这个大长方形的周长是(
)cm.如果给你5个长2cm、宽1cm的小长方形,你能把它们按照这种方式摆出一个大长方形吗?如果能,请你画出示意图;如果不能,请你说明理由.
(2)小宇用5个小长方形按照第(1)题中的方式摆出了一个更大的长方形.他所用的小长方形的长、宽可能是多少?请你写出2种,填在下表中.
长/cm
宽/cm
根据上面的探索,我发现所用的小长方形的长和宽之间有这样的规律:
。
5.有一个长方体,如图,(单位:厘米)现将它“切成”完全一样的三个长方体.(1)共有
种切法.(2)怎样切,使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,算一算表面积最多增加了多少?
答案
一、选择题
1.D2.C3.B4.A5.C6.D7.D
8.B
9.A10.A11.C12.D13.A14.B15.A16.D
二、填空题
1.4500立方厘米
2.1.8
3.M
Q
P
N
4.3、4、5或6、7
5.16.8
6.D
B
顺
180
逆
180
7.5
8.;
9.396
10.45
三、判断题
1.×2.×3.√4.×5.√6.√
四.图形计算题
1.
2.
(长方)形+(梯)形
(长方)形+(三角)形
(梯)形+(三角)形
3.画图如下:
4.切3刀如图:
.
【详解】把这块豆腐分成8小块,最少要切三刀,即纵切两刀,横切一刀.纵切一刀时,即可切成2小块,再纵切一刀,要与第一次的切缝交叉,这样就分成4块,再横切一刀,即可把分成的这4小块再一分为二,就是8小块.
5.
6.
7.
如图所示:
8.作图如下:
(答案不唯一)
五、应用题
1.
答:原来长方体的表面积是210平方厘米。
2.所有的黑皮的边数:12×5=60,一块白皮的边数是6,则白皮的数量为:
60×2÷6=120÷6=20(块)
答:白皮有20块。
3.底面半径:120÷20÷2=3(厘米)
体积:3.14×32×20=565.2(立方厘米)
答:这圆柱的体积是565.2立方厘米。
4.(1)44;不能,因为:按着这种方式摆长方形的长一边是2+2=4(cm),另一边是1+1+1=3(cm),一个长方形的两个长不相等,所以不能.
(2)
长/cm
12
18
宽/cm
8
12
小长方形的长和宽之间有这样的规律:长:宽=3:2
5.(1)有三种切法,
①24÷3=8,可以切长为12、宽为8、高为6的三个长方体;
②12÷3=4,可以切成长为24宽为4高为6的三个长方体;
③6÷3=2可以切成长为24宽为12高为2的三个长方体.故答案为3.
(2)第三种切法使切成三块后的长方体的表面积的和比原来长方体的表面积增加得最多,
增加的是长为24宽为12的四个面的面积:24×12×4=1152.
答:表面积增加了1152平方厘米.
