六年级数学下册试题 一课一练《图形与几何-图形的认识与测量》- 教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《图形与几何-图形的认识与测量》- 教版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 692.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览



文档简介
《图形与几何-图形的认识与测量》
一、选择题(每题1分,共16分)
1.下图中,的大小是(
)。
A.
B.
C.
D.
2.用一副三角板不可能拼出(
)的角。
A.
B.
C.
D.
3.用三根同样长的绳子分别围成长方形、正方形和圆,(
)的面积最大。
A.长方形
B.正方形
C.圆
4.要剪一个面积是12.56平方厘米的圆形纸片,至少需要面积是(
)平方厘米的正方形纸片(π取3.14)。
A.12.56
B.16
C.18
D.25
5.把一个平行四边形任意分割成两个梯形,这两个梯形的(
)总相等。
A.面积
B.高
C.上、下底的和
6.等腰直角三角形三个内角度数之比是( )
A.1:2:2
B.2:1:1
C.3:2:1
7.将一个平行四边形拉成一个长方形前后,图形的(
)。
A.面积变大,周长变小
B.面积变大,周长不变
C.面积不变,周长不变
8.三角形的一条边长5厘米,另一条边长7厘米,那么这个三角形第三条边c的取值范围是(
)厘米。
A.5<c<7
B.7<c<12
C.2<c<12
D.2<c<7
9.小明用一张梯形纸做折纸游戏.先上下对折,使两底重合,可得图①,并测出未重叠部分的两个三角形面积和是20平方厘米.然后再将图①中两个小三角形部分向内翻折,得到图②.经测算,图②的面积相当于图①的.这张梯形纸的面积是(
)平方厘米.
A.50
B.60
C.100
D.120
10.下面说法错误的是(
)。
A.三角形的内角和是180°
B.一个三角形中最多有一个钝角
C.等边三角形是特殊的等腰三角形
D.正方形、长方形和梯形都是特殊的平行四边形
11.如图,在一个上底和下底分别是10、20的梯形中,阴影部分面积为40平方厘米,则空白部分的面积是( )平方厘米。
A.20
B.40
C.60
12.过平行四边形的一个顶点最多可以向对边作(
)条高。
A.1
B.2
C.无数
13.如图,已知AB为大圆的直径,每个小圆的直径相同,大圆的面积为360平方厘米,则8个小圆的面积之和等于(
)平方厘米。
A.80
B.60
C.20
D.10
14.如图,宽为50厘米的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积是(
)平方厘米。
A.400?
B.500?
C.600??
D.300
15.下图中三个组合图形的面积比较,(
)。
A.(1)号面积最大
B.(2)号面积最大
C.(3)号面积最大
D.三个面积一样大
16.如图,四边形ABCD是平行四边形,BE:EC=1:2,F是DC的中点,三角形ABE的面积是12cm2,
那么三角形ADF的面积是(
??).
A.36cm2
B.12cm2
C.24cm2
D.18cm2
二、填空题(每空1分,共19分)
1.用一张长和宽之比为的纸剪两个最大的圆,这张纸的利用率是(________)。
2.正方形网格中,小方格的顶点叫作格点。如图,每个小方格都是边长为1的正方形,A、B两点在正方形网格的格点上,点C也在格点上,且为等腰三角形,则符合条件的格点C共有(______)个。
3.一个直角梯形高,把它的下底缩短成一个点,就得到一个等腰直角三角形,面积变成了原来梯形的,原来梯形的面积是(________)。
4.在一个周长是的圆内,画一个以该圆的直径为底边的最大的三角形,这个三角形的面积是(________)。
5.下图中线段长,绕O点逆时针旋转到线段,所构成的图形是(________)形,这个图形的周长是(________)。
6.如图,的面积和正方形的面积之比是,正方形的边长为8厘米,则的面积是____平方厘米。
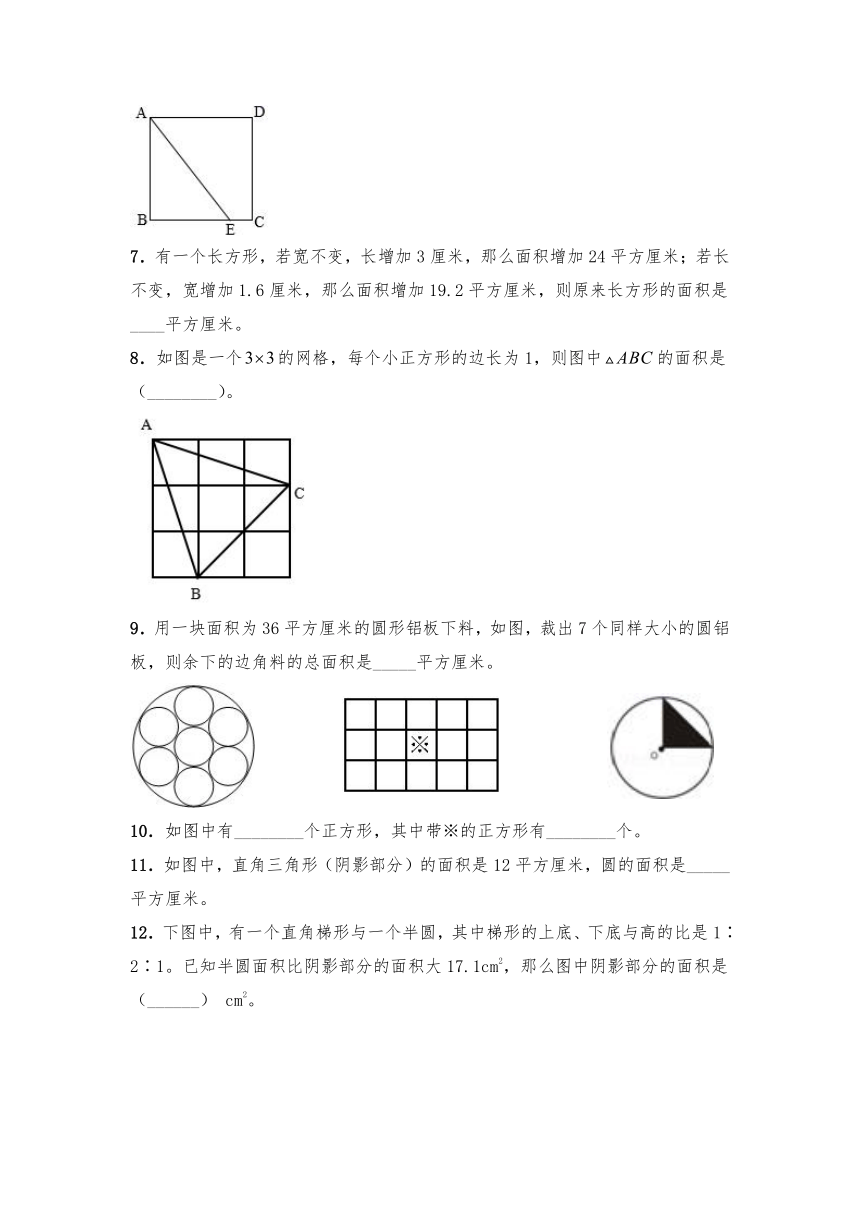
7.有一个长方形,若宽不变,长增加3厘米,那么面积增加24平方厘米;若长不变,宽增加1.6厘米,那么面积增加19.2平方厘米,则原来长方形的面积是____平方厘米。
8.如图是一个的网格,每个小正方形的边长为1,则图中的面积是(________)。
9.用一块面积为36平方厘米的圆形铝板下料,如图,裁出7个同样大小的圆铝板,则余下的边角料的总面积是_____平方厘米。
10.如图中有________个正方形,其中带※的正方形有________个。
11.如图中,直角三角形(阴影部分)的面积是12平方厘米,圆的面积是_____平方厘米。
12.下图中,有一个直角梯形与一个半圆,其中梯形的上底、下底与高的比是1∶2∶1。已知半圆面积比阴影部分的面积大17.1cm2,那么图中阴影部分的面积是(______)
cm2。
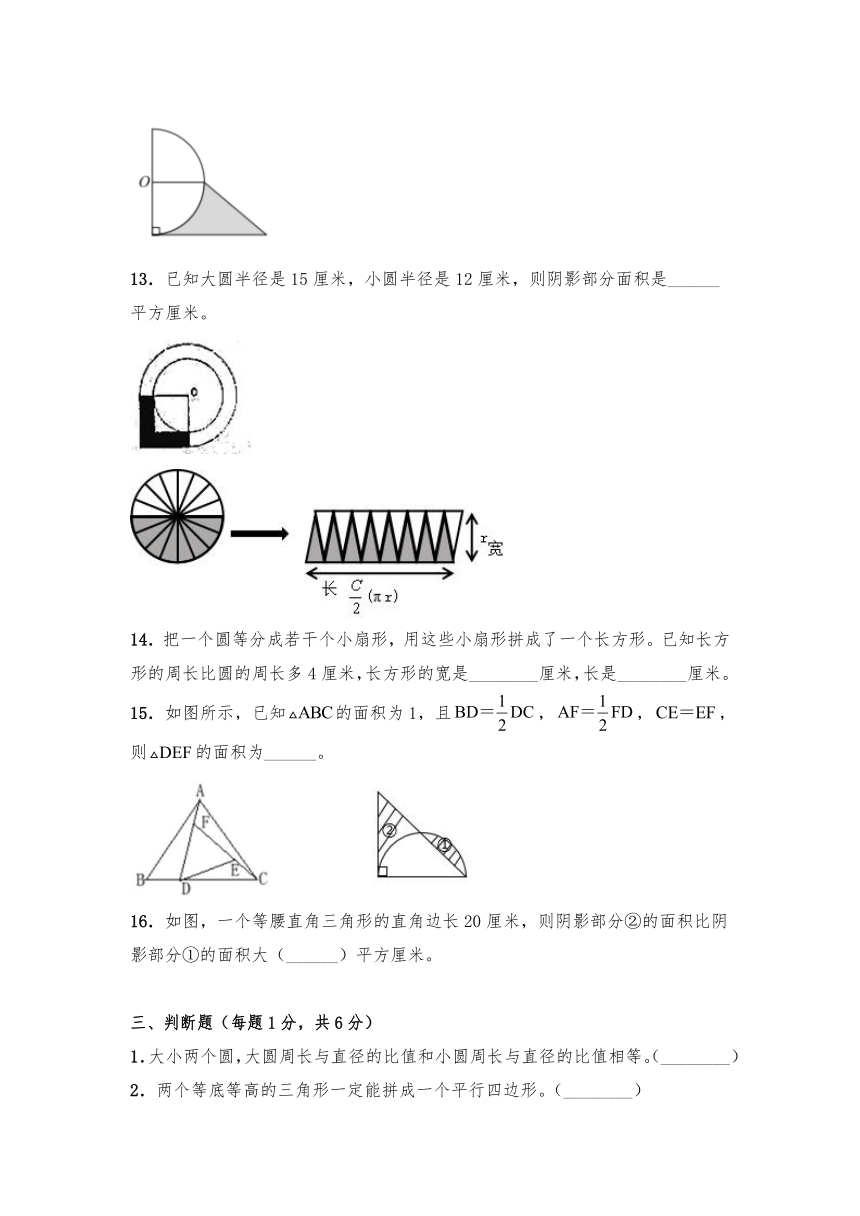
13.已知大圆半径是15厘米,小圆半径是12厘米,则阴影部分面积是______平方厘米。
14.把一个圆等分成若干个小扇形,用这些小扇形拼成了一个长方形。已知长方形的周长比圆的周长多4厘米,长方形的宽是________厘米,长是________厘米。
15.如图所示,已知的面积为1,且,,,则的面积为______。
16.如图,一个等腰直角三角形的直角边长20厘米,则阴影部分②的面积比阴影部分①的面积大(______)平方厘米。
三、判断题(每题1分,共6分)
1.大小两个圆,大圆周长与直径的比值和小圆周长与直径的比值相等。(________)
2.两个等底等高的三角形一定能拼成一个平行四边形。(________)
3.两个等底等高的三角形的形状不一定相同,但它们的面积一定相等。(________)
4.大于90°的角是钝角。(________)
5.如果平行四边形的面积是三角形面积的2倍,那么它们一定等底等高.(_____)
6.半径是2厘米的圆,它的周长和面积相等._____
四.图形计算题(29分)
1.求下列各图形中涂色部分的面积。(单位:
cm)(6分)
2.求涂色部分的面积。(单位:厘米)(4分)
3.计算下图中阴影部分的面积。(5分)
4.三角形是等腰直角三角形,以为直径,中点为圆心画半圆,为半圆周的中点,连结,已知厘米,求阴影部分的面积。(5分)
5.在长方形ABCD中,AD=15厘米,AB=8厘米,四边形EFGO的面积是9平方厘米,阴影部分的面积是多少平方厘米?(5分)
6.在图中,甲、乙都是正方形,边长分别为
10
厘米和
12
厘米,则阴影部分的面积是多少平方厘米?(4分)
五、应用题(每题5分,共30分)
1.的三个内角度数比是:。
(1)根据这个比判断:这个三角形(
)等腰直角三角形。(填是或不是)写出你的判断方法:(2)这个三角形的面积是8平方厘米,请你在下面方格图(每个小正方形的边长是)中画出这个三角形。
2.
方法一:
方法二:
方法三:
①如果接头处不计,方法二至少需要多长的绳子?②观察这三种捆扎方法,你有什么发现?
3.问题:学校运动场如图①,两端是半圆形,中间是正方形运动场,周长是257米。这个运动场的周长是多少米?
(1)分析与解答:某小组采取合作学习的方式探究此问题,以下是该小组三位同学的对话:
甲:“把运动场进行平移变换(如图②),则圆的周长+正方形边长×2=运动场周长。”
乙:“圆的周长可以看作是正方形边长的3.14倍。”丙:“我们可以用方程的思想来解决问题!”
亲爱的同学,请你帮助他们完成解答。(2)拓展延伸:学校计划在此运动场内部修建一条宽是5米的塑胶跑道(图③中阴影部分),每平方米塑胶跑道的造价是80元,一共需要多少元?
4.把一张边长4厘米的正方形纸片,按图1、2的方式依次沿虚线对折后,再沿图3中的虚线在左上角剪去一个边长0.5厘米的正方形,下边居中剪去一个长1厘米、宽0.5厘米的长方形即如图4,最后把图4中的纸片打开铺平。请你画出铺平后的纸片形状。铺平后纸片的面积是多少平方厘米?
5.仔细看图,活学活用。
(1)画出三角形的边上的高。
(2)根据图中提供的信息,不用测量任何数据,画一个与三角形面积相等的三角形
(3)应用:在如图所示的梯形中,三角形与三角形的面积分别是4平方厘米和9平方厘米。梯形的面积是(
)。
6.如下图所示,把三角形DBE沿线段AC折叠,得到一个多边形DACEFBG,这个多边形的面积与原三角形面积的比是5:7,已知右下图中阴影部分的面积为120平方厘米,求原来三角形的面积是多少?
答案
一、选择题
1.C
2.C
3.C
4.B
5.B6.B7.B8.C
9.C10.D11.A12.B13.A14.A15.D16.D
二、填空题
1.78.5%
2.9
3.128
4.4
5.扇
18.28
6.24
7.96
8.4
9.8
10.26
8
11.75.36
12.14.3
13.81
14.2
6.28
15.
16.43
三、判断题
1.√2.×3.√4.×5.×6.×
四.图形计算题
1.(1)梯形的面积:(4+9)×6÷2=13×6÷2=39(平方厘米)
空白三角形的面积:4×6÷2=12(平方厘米)涂色部分的面积:39-12=27(平方厘米)
(2)扇形的面积:3.14××=3.14(平方厘米)
三角形的面积:2×2÷2=2(平方厘米)
涂色部分的面积:3.14-2=1.14(平方厘米)
2.(4+8)×4÷2=12×2=24(平方厘米)
3.沿虚线剪拼如下:
由图可知阴影部分面积=半圆面积-三角形面积。
3.14×(20÷2)2÷2-(20÷2)×(20÷2)÷2=3.14×50-100÷2=157-50=107(平方厘米)
4.如图作出辅助线:
则空白部分的面积为三角形AED的面积减去正方形BEDO的面积再加上圆面积的,
三角形AED的面积是:(10+10÷2)×(10÷2)×,正方形面积是:(10÷2)?,
圆面积的是:×3.14×(10÷2)?,
故空白部分面积为:(10+10÷2)×(10÷2)×-(10÷2)?+×3.14×(10÷2)?
=15×5×-25+×3.14×25=37.5-25+19.625=32.125(平方厘米)
所以阴影部分的面积为:10×10÷2+3.14×(10÷2)?÷2-32.125=50+39.25-32.125=57.125(平方厘米)故答案为:57.125平方厘米
5.由图示得:其中△DBF和△AFC是等高的三角形,所以2个三角形面积和=(BF+CF)×AB÷2=BC×AB÷2,又因为四边形EFGO在两个三角形中,重复减了两次,要再加上一次,阴影部分面积=长方形ABCD的面积﹣(△DBF的面积+△AFC的面积)+9.
解:15×8﹣15×8÷2+9=120﹣60+9=69(平方厘米).
答:阴影部分的面积是69平方厘米.
6.(10+12)×10÷2+3.14×122÷4﹣10×(10+12)÷2=110+113.04-110=113.04(平方厘米)
答:阴影部分的面积是113.04平方厘米。
五、应用题
1.(1)根据这个比判断:这个三角形(是)等腰直角三角形。
因为最大角为180°×=90°,有一个角是直角的三角形是直角三角形,并且三角形中的另外2个角相等,所以这个三角形是等腰直角三角形。
(2)因为4×4=8×2,所以等腰直角三角形的腰长为4厘米。
作图如下:
2.①3.14×7+7×6=21.98+42=63.98(cm)
答:如果接头处不计,方法二至少需要63.98cm的绳子。
②发现三种捆法的周长均等于1个小圆的周长加若干直径(答案合理即可)
3.(1)①257÷4=64.25(米)
3.14×64.25+64.25×2=201.745+128.5=330.245(米)
②257÷4×3.14+257÷4×2=201.745+128.5=330.245(米)
③设正方形的边长为x米,
4x=257
x=257÷4
x=64.25
64.25×3.14+64.25×2=201.745+128.5=330.245(米)
答:这个运动场的周长是330.245米。
(2)64.25÷2=32.125(米)
32.125﹣5=27.125(米)
3.14×(32.1252﹣27.1252)+64.25×5×2=3.14×(1032.015625﹣735.765625)+642.5
=3.14×296.25+642.5=930.225+642.5=1572.725(平方米)
1572.725×80=125818(元)
答:一共需要125818元。
4.平铺后图形如下:
4×4-0.5×1×4-1×1=16-2-1=13(平方厘米)
答:铺平后纸片的面积是13平方厘米。
5.
(1)
(2)
(3)根据蝴蝶定理,梯形左、右两部分面积都是6平方厘米,梯形的面积=4+9+6+6=25(平方厘米)
6.120÷[1-(7-5)÷7×2]=120÷[1-]=120÷=280(平方厘米)
答:原来三角形的面积是280平方厘米。
一、选择题(每题1分,共16分)
1.下图中,的大小是(
)。
A.
B.
C.
D.
2.用一副三角板不可能拼出(
)的角。
A.
B.
C.
D.
3.用三根同样长的绳子分别围成长方形、正方形和圆,(
)的面积最大。
A.长方形
B.正方形
C.圆
4.要剪一个面积是12.56平方厘米的圆形纸片,至少需要面积是(
)平方厘米的正方形纸片(π取3.14)。
A.12.56
B.16
C.18
D.25
5.把一个平行四边形任意分割成两个梯形,这两个梯形的(
)总相等。
A.面积
B.高
C.上、下底的和
6.等腰直角三角形三个内角度数之比是( )
A.1:2:2
B.2:1:1
C.3:2:1
7.将一个平行四边形拉成一个长方形前后,图形的(
)。
A.面积变大,周长变小
B.面积变大,周长不变
C.面积不变,周长不变
8.三角形的一条边长5厘米,另一条边长7厘米,那么这个三角形第三条边c的取值范围是(
)厘米。
A.5<c<7
B.7<c<12
C.2<c<12
D.2<c<7
9.小明用一张梯形纸做折纸游戏.先上下对折,使两底重合,可得图①,并测出未重叠部分的两个三角形面积和是20平方厘米.然后再将图①中两个小三角形部分向内翻折,得到图②.经测算,图②的面积相当于图①的.这张梯形纸的面积是(
)平方厘米.
A.50
B.60
C.100
D.120
10.下面说法错误的是(
)。
A.三角形的内角和是180°
B.一个三角形中最多有一个钝角
C.等边三角形是特殊的等腰三角形
D.正方形、长方形和梯形都是特殊的平行四边形
11.如图,在一个上底和下底分别是10、20的梯形中,阴影部分面积为40平方厘米,则空白部分的面积是( )平方厘米。
A.20
B.40
C.60
12.过平行四边形的一个顶点最多可以向对边作(
)条高。
A.1
B.2
C.无数
13.如图,已知AB为大圆的直径,每个小圆的直径相同,大圆的面积为360平方厘米,则8个小圆的面积之和等于(
)平方厘米。
A.80
B.60
C.20
D.10
14.如图,宽为50厘米的长方形图案由10个相同的小长方形拼成,其中一个小长方形的面积是(
)平方厘米。
A.400?
B.500?
C.600??
D.300
15.下图中三个组合图形的面积比较,(
)。
A.(1)号面积最大
B.(2)号面积最大
C.(3)号面积最大
D.三个面积一样大
16.如图,四边形ABCD是平行四边形,BE:EC=1:2,F是DC的中点,三角形ABE的面积是12cm2,
那么三角形ADF的面积是(
??).
A.36cm2
B.12cm2
C.24cm2
D.18cm2
二、填空题(每空1分,共19分)
1.用一张长和宽之比为的纸剪两个最大的圆,这张纸的利用率是(________)。
2.正方形网格中,小方格的顶点叫作格点。如图,每个小方格都是边长为1的正方形,A、B两点在正方形网格的格点上,点C也在格点上,且为等腰三角形,则符合条件的格点C共有(______)个。
3.一个直角梯形高,把它的下底缩短成一个点,就得到一个等腰直角三角形,面积变成了原来梯形的,原来梯形的面积是(________)。
4.在一个周长是的圆内,画一个以该圆的直径为底边的最大的三角形,这个三角形的面积是(________)。
5.下图中线段长,绕O点逆时针旋转到线段,所构成的图形是(________)形,这个图形的周长是(________)。
6.如图,的面积和正方形的面积之比是,正方形的边长为8厘米,则的面积是____平方厘米。
7.有一个长方形,若宽不变,长增加3厘米,那么面积增加24平方厘米;若长不变,宽增加1.6厘米,那么面积增加19.2平方厘米,则原来长方形的面积是____平方厘米。
8.如图是一个的网格,每个小正方形的边长为1,则图中的面积是(________)。
9.用一块面积为36平方厘米的圆形铝板下料,如图,裁出7个同样大小的圆铝板,则余下的边角料的总面积是_____平方厘米。
10.如图中有________个正方形,其中带※的正方形有________个。
11.如图中,直角三角形(阴影部分)的面积是12平方厘米,圆的面积是_____平方厘米。
12.下图中,有一个直角梯形与一个半圆,其中梯形的上底、下底与高的比是1∶2∶1。已知半圆面积比阴影部分的面积大17.1cm2,那么图中阴影部分的面积是(______)
cm2。
13.已知大圆半径是15厘米,小圆半径是12厘米,则阴影部分面积是______平方厘米。
14.把一个圆等分成若干个小扇形,用这些小扇形拼成了一个长方形。已知长方形的周长比圆的周长多4厘米,长方形的宽是________厘米,长是________厘米。
15.如图所示,已知的面积为1,且,,,则的面积为______。
16.如图,一个等腰直角三角形的直角边长20厘米,则阴影部分②的面积比阴影部分①的面积大(______)平方厘米。
三、判断题(每题1分,共6分)
1.大小两个圆,大圆周长与直径的比值和小圆周长与直径的比值相等。(________)
2.两个等底等高的三角形一定能拼成一个平行四边形。(________)
3.两个等底等高的三角形的形状不一定相同,但它们的面积一定相等。(________)
4.大于90°的角是钝角。(________)
5.如果平行四边形的面积是三角形面积的2倍,那么它们一定等底等高.(_____)
6.半径是2厘米的圆,它的周长和面积相等._____
四.图形计算题(29分)
1.求下列各图形中涂色部分的面积。(单位:
cm)(6分)
2.求涂色部分的面积。(单位:厘米)(4分)
3.计算下图中阴影部分的面积。(5分)
4.三角形是等腰直角三角形,以为直径,中点为圆心画半圆,为半圆周的中点,连结,已知厘米,求阴影部分的面积。(5分)
5.在长方形ABCD中,AD=15厘米,AB=8厘米,四边形EFGO的面积是9平方厘米,阴影部分的面积是多少平方厘米?(5分)
6.在图中,甲、乙都是正方形,边长分别为
10
厘米和
12
厘米,则阴影部分的面积是多少平方厘米?(4分)
五、应用题(每题5分,共30分)
1.的三个内角度数比是:。
(1)根据这个比判断:这个三角形(
)等腰直角三角形。(填是或不是)写出你的判断方法:(2)这个三角形的面积是8平方厘米,请你在下面方格图(每个小正方形的边长是)中画出这个三角形。
2.
方法一:
方法二:
方法三:
①如果接头处不计,方法二至少需要多长的绳子?②观察这三种捆扎方法,你有什么发现?
3.问题:学校运动场如图①,两端是半圆形,中间是正方形运动场,周长是257米。这个运动场的周长是多少米?
(1)分析与解答:某小组采取合作学习的方式探究此问题,以下是该小组三位同学的对话:
甲:“把运动场进行平移变换(如图②),则圆的周长+正方形边长×2=运动场周长。”
乙:“圆的周长可以看作是正方形边长的3.14倍。”丙:“我们可以用方程的思想来解决问题!”
亲爱的同学,请你帮助他们完成解答。(2)拓展延伸:学校计划在此运动场内部修建一条宽是5米的塑胶跑道(图③中阴影部分),每平方米塑胶跑道的造价是80元,一共需要多少元?
4.把一张边长4厘米的正方形纸片,按图1、2的方式依次沿虚线对折后,再沿图3中的虚线在左上角剪去一个边长0.5厘米的正方形,下边居中剪去一个长1厘米、宽0.5厘米的长方形即如图4,最后把图4中的纸片打开铺平。请你画出铺平后的纸片形状。铺平后纸片的面积是多少平方厘米?
5.仔细看图,活学活用。
(1)画出三角形的边上的高。
(2)根据图中提供的信息,不用测量任何数据,画一个与三角形面积相等的三角形
(3)应用:在如图所示的梯形中,三角形与三角形的面积分别是4平方厘米和9平方厘米。梯形的面积是(
)。
6.如下图所示,把三角形DBE沿线段AC折叠,得到一个多边形DACEFBG,这个多边形的面积与原三角形面积的比是5:7,已知右下图中阴影部分的面积为120平方厘米,求原来三角形的面积是多少?
答案
一、选择题
1.C
2.C
3.C
4.B
5.B6.B7.B8.C
9.C10.D11.A12.B13.A14.A15.D16.D
二、填空题
1.78.5%
2.9
3.128
4.4
5.扇
18.28
6.24
7.96
8.4
9.8
10.26
8
11.75.36
12.14.3
13.81
14.2
6.28
15.
16.43
三、判断题
1.√2.×3.√4.×5.×6.×
四.图形计算题
1.(1)梯形的面积:(4+9)×6÷2=13×6÷2=39(平方厘米)
空白三角形的面积:4×6÷2=12(平方厘米)涂色部分的面积:39-12=27(平方厘米)
(2)扇形的面积:3.14××=3.14(平方厘米)
三角形的面积:2×2÷2=2(平方厘米)
涂色部分的面积:3.14-2=1.14(平方厘米)
2.(4+8)×4÷2=12×2=24(平方厘米)
3.沿虚线剪拼如下:
由图可知阴影部分面积=半圆面积-三角形面积。
3.14×(20÷2)2÷2-(20÷2)×(20÷2)÷2=3.14×50-100÷2=157-50=107(平方厘米)
4.如图作出辅助线:
则空白部分的面积为三角形AED的面积减去正方形BEDO的面积再加上圆面积的,
三角形AED的面积是:(10+10÷2)×(10÷2)×,正方形面积是:(10÷2)?,
圆面积的是:×3.14×(10÷2)?,
故空白部分面积为:(10+10÷2)×(10÷2)×-(10÷2)?+×3.14×(10÷2)?
=15×5×-25+×3.14×25=37.5-25+19.625=32.125(平方厘米)
所以阴影部分的面积为:10×10÷2+3.14×(10÷2)?÷2-32.125=50+39.25-32.125=57.125(平方厘米)故答案为:57.125平方厘米
5.由图示得:其中△DBF和△AFC是等高的三角形,所以2个三角形面积和=(BF+CF)×AB÷2=BC×AB÷2,又因为四边形EFGO在两个三角形中,重复减了两次,要再加上一次,阴影部分面积=长方形ABCD的面积﹣(△DBF的面积+△AFC的面积)+9.
解:15×8﹣15×8÷2+9=120﹣60+9=69(平方厘米).
答:阴影部分的面积是69平方厘米.
6.(10+12)×10÷2+3.14×122÷4﹣10×(10+12)÷2=110+113.04-110=113.04(平方厘米)
答:阴影部分的面积是113.04平方厘米。
五、应用题
1.(1)根据这个比判断:这个三角形(是)等腰直角三角形。
因为最大角为180°×=90°,有一个角是直角的三角形是直角三角形,并且三角形中的另外2个角相等,所以这个三角形是等腰直角三角形。
(2)因为4×4=8×2,所以等腰直角三角形的腰长为4厘米。
作图如下:
2.①3.14×7+7×6=21.98+42=63.98(cm)
答:如果接头处不计,方法二至少需要63.98cm的绳子。
②发现三种捆法的周长均等于1个小圆的周长加若干直径(答案合理即可)
3.(1)①257÷4=64.25(米)
3.14×64.25+64.25×2=201.745+128.5=330.245(米)
②257÷4×3.14+257÷4×2=201.745+128.5=330.245(米)
③设正方形的边长为x米,
4x=257
x=257÷4
x=64.25
64.25×3.14+64.25×2=201.745+128.5=330.245(米)
答:这个运动场的周长是330.245米。
(2)64.25÷2=32.125(米)
32.125﹣5=27.125(米)
3.14×(32.1252﹣27.1252)+64.25×5×2=3.14×(1032.015625﹣735.765625)+642.5
=3.14×296.25+642.5=930.225+642.5=1572.725(平方米)
1572.725×80=125818(元)
答:一共需要125818元。
4.平铺后图形如下:
4×4-0.5×1×4-1×1=16-2-1=13(平方厘米)
答:铺平后纸片的面积是13平方厘米。
5.
(1)
(2)
(3)根据蝴蝶定理,梯形左、右两部分面积都是6平方厘米,梯形的面积=4+9+6+6=25(平方厘米)
6.120÷[1-(7-5)÷7×2]=120÷[1-]=120÷=280(平方厘米)
答:原来三角形的面积是280平方厘米。
