2020-2021学年沪科新版七年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年沪科新版七年级下册数学期末练习试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 221.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 15:27:56 | ||
图片预览


文档简介
2020-2021学年沪科新版七年级下册数学期末练习试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列各数:﹣1,,1.1212212221…(每两个1之间增加1个2),﹣3.1415,,﹣0.,其中无理数有( )
A.1个
B.2个
C.3个
D.4个
2.下面调查统计中,适合采用普查方式的是( )
A.华为手机的市场占有率
B.乘坐飞机的旅客是否携带了违禁物品
C.国家宝藏”专栏电视节目的收视率
D.“现代”汽车每百公里的耗油量
3.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2
B.﹣a<﹣b
C.a﹣3>b﹣3
D.1﹣2a>1﹣2b
4.已知方程mx+2y=﹣2,当x=3时y=5,那么m为( )
A.
B.﹣
C.﹣4
D.
5.如果不等式(a﹣3)x>a﹣3的解集是x<1,那么a的取值范围是( )
A.a>0
B.a<0
C.a>3
D.a<3
6.下列选项中,可以用来证明命题“若a>b,则|a|>|b|”是假命题的反例是( )
A.a=1,b=0
B.a=1,b=﹣2
C.a=﹣2,b=1
D.a=2,b=﹣1
7.如图所示,OB⊥OD,OC⊥OA,∠BOC=32°,那么∠AOD等于( )
A.148°
B.132°
C.128°
D.90°
8.如图,△ABC顶点C的坐标是(﹣3,2),过点C作AB上的高线CD,则垂足D点的坐标为( )
A.(2,0)
B.(﹣3,0)
C.(0,2)
D.(0,﹣3)
9.在抗击疫情网络知识竞赛中,为奖励成绩突出的学生,学校计划用200元钱购买A、B、C三种奖品,A种每个10元,B种每个20元,C种每个30元,在C种奖品不超过两个且钱全部用完的情况下,有多少种购买方案( )
A.12种
B.15种
C.16种
D.14种
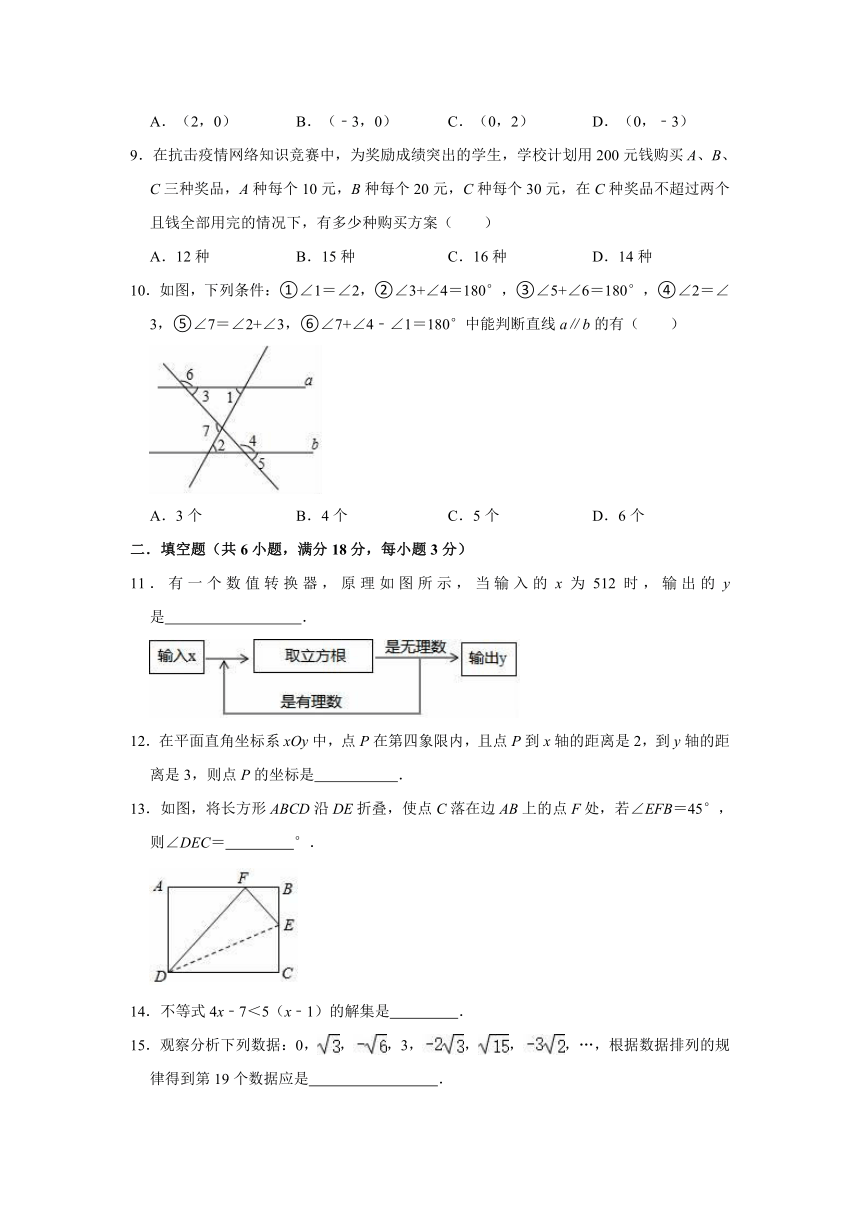
10.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个
B.4个
C.5个
D.6个
二.填空题(共6小题,满分18分,每小题3分)
11.有一个数值转换器,原理如图所示,当输入的x为512时,输出的y是
.
12.在平面直角坐标系xOy中,点P在第四象限内,且点P到x轴的距离是2,到y轴的距离是3,则点P的坐标是
.
13.如图,将长方形ABCD沿DE折叠,使点C落在边AB上的点F处,若∠EFB=45°,则∠DEC=
°.
14.不等式4x﹣7<5(x﹣1)的解集是
.
15.观察分析下列数据:0,,,3,,,,…,根据数据排列的规律得到第19个数据应是
.
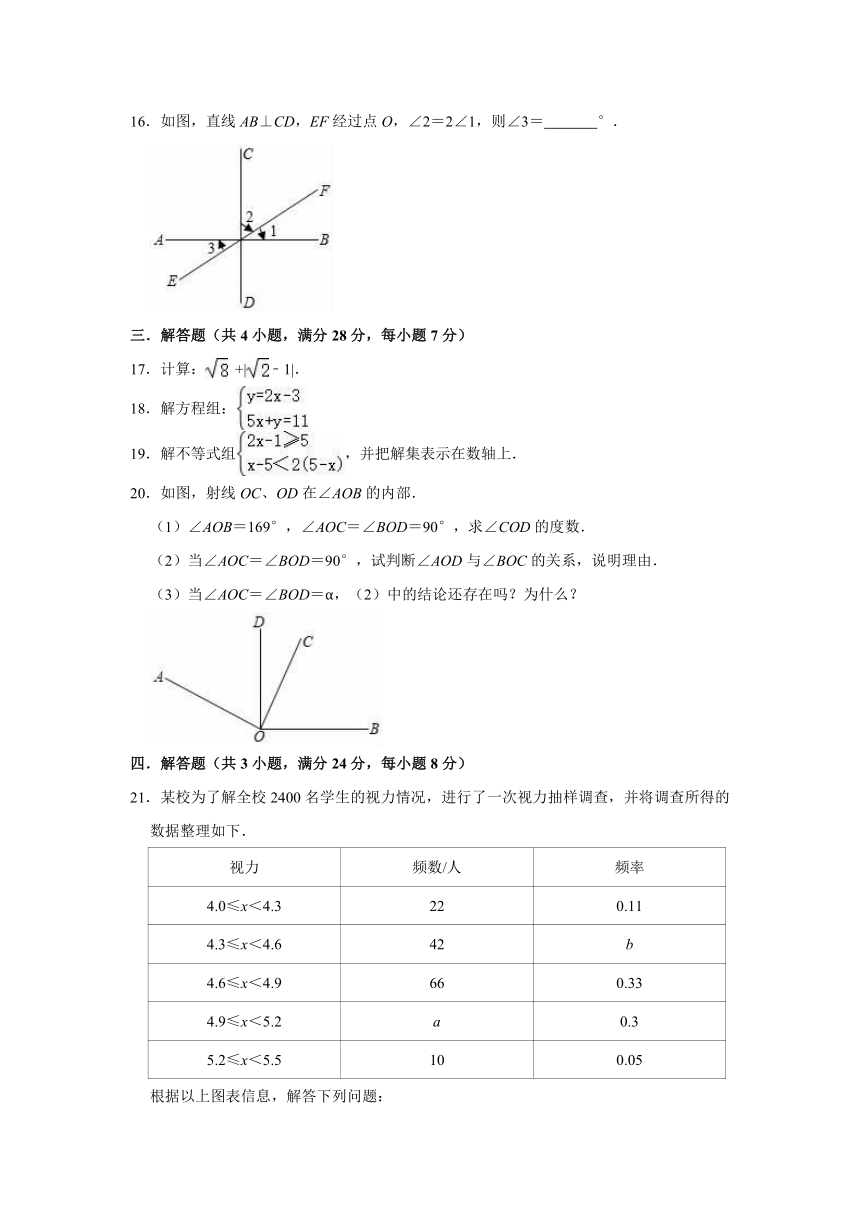
16.如图,直线AB⊥CD,EF经过点O,∠2=2∠1,则∠3=
°.
三.解答题(共4小题,满分28分,每小题7分)
17.计算:
+|﹣1|.
18.解方程组:
19.解不等式组,并把解集表示在数轴上.
20.如图,射线OC、OD在∠AOB的内部.
(1)∠AOB=169°,∠AOC=∠BOD=90°,求∠COD的度数.
(2)当∠AOC=∠BOD=90°,试判断∠AOD与∠BOC的关系,说明理由.
(3)当∠AOC=∠BOD=α,(2)中的结论还存在吗?为什么?
四.解答题(共3小题,满分24分,每小题8分)
21.某校为了解全校2400名学生的视力情况,进行了一次视力抽样调查,并将调查所得的数据整理如下.
视力
频数/人
频率
4.0≤x<4.3
22
0.11
4.3≤x<4.6
42
b
4.6≤x<4.9
66
0.33
4.9≤x<5.2
a
0.3
5.2≤x<5.5
10
0.05
根据以上图表信息,解答下列问题:
(1)表中的a=
,b=
.
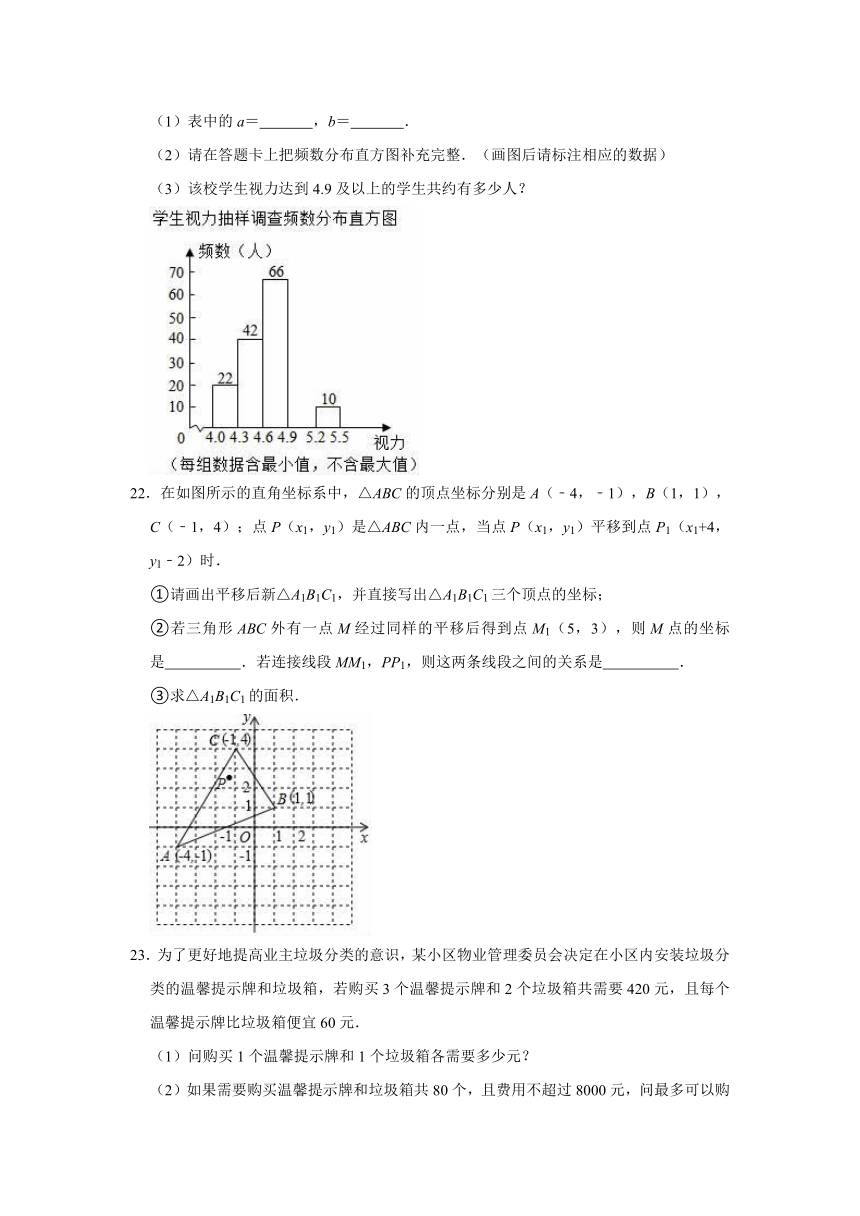
(2)请在答题卡上把频数分布直方图补充完整.(画图后请标注相应的数据)
(3)该校学生视力达到4.9及以上的学生共约有多少人?
22.在如图所示的直角坐标系中,△ABC的顶点坐标分别是A(﹣4,﹣1),B(1,1),C(﹣1,4);点P(x1,y1)是△ABC内一点,当点P(x1,y1)平移到点P1(x1+4,y1﹣2)时.
①请画出平移后新△A1B1C1,并直接写出△A1B1C1三个顶点的坐标;
②若三角形ABC外有一点M经过同样的平移后得到点M1(5,3),则M点的坐标是
.若连接线段MM1,PP1,则这两条线段之间的关系是
.
③求△A1B1C1的面积.
23.为了更好地提高业主垃圾分类的意识,某小区物业管理委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和2个垃圾箱共需要420元,且每个温馨提示牌比垃圾箱便宜60元.
(1)问购买1个温馨提示牌和1个垃圾箱各需要多少元?
(2)如果需要购买温馨提示牌和垃圾箱共80个,且费用不超过8000元,问最多可以购买垃圾箱多少个?
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:﹣1是整数,属于有理数;
﹣3.1415是有限小数,属于有理数;
是分数,属于有理数;
﹣0.是循环小数,属于有理数;
无理数有,1.1212212221…(每两个1之间增加1个2)共2个.
故选:B.
2.解:A、对华为手机的市场占有率的调查范围广,适合抽样调查,故此选项不符合题意;
B、对乘坐飞机的旅客是否携带了违禁物品的调查情况适合普查,故此选项符合题意;
C、对国家宝藏”专栏电视节目的收视率的调查范围广,适合抽样调查,故此选项不符合题意;
D、对“现代”汽车每百公里的耗油量的调查范围广适合抽样调查,故此选项不符合题意;
故选:B.
3.解:A、∵a>b,∴a+2>b+2,故A正确,不符合题意.
B、∵a>b,∵﹣a<﹣b.故B正确,不符合题意.
C、∵a>b,∴a﹣3>b﹣3,故C正确,不符合题意.
D、∵a>b,∴﹣2a<﹣2b,∴1﹣2a<1﹣2b.故D错误,符合题意.
故选:D.
4.解:把x=3,y=5代入方程得:3m+10=﹣2,
移项合并得:3m=﹣12,
解得:m=﹣4,
故选:C.
5.解:∵(a﹣3)x>a﹣3的解集是x<1,
∴a﹣3<0,
解得a<3,
故选:D.
6.解:当a=1,b=﹣2时,a>b,但|a|<|b|,
故选:B.
7.解:∵OB⊥OD,所以∠BOD=90°
∵OC⊥OA
∴∠AOC=90°
∴∠AOB=∠AOC﹣∠BOC=90°﹣32°=58°
∴∠AOD=∠AOB+∠BOD=90°+58°=148°
故选:A.
8.解:过点C作CD垂直于x轴,垂足为D,
∵点C(﹣3,2),
∴点D横坐标与点C横坐标相等,
∴点D(﹣3,0).
故选:B.
9.解:设购买A种奖品m个,购买B种奖品n个,
当C种奖品个数为1个时,
根据题意得10m+20n+30=200,
整理得m+2n=17,
∵m、n都是正整数,0<2n<17,
∴n=1,2,3,4,5,6,7,8;
当C种奖品个数为2个时,
根据题意得10m+20n+60=200,
整理得m+2n=14,
∵m、n都是正整数,0<2n<14,
∴n=1,2,3,4,5,6;
∴有8+6=14种购买方案.
故选:D.
10.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.解:由题中所给的程序可知:把512取立方根,结果为8,
因为8是有理数,所以再取立方根为2,
2是有理数,所以再取立方根为,
因为是无理数,输出,
故答案为:.
12.解:若点P在第四象限,且点P到x轴的距离为2,到y轴的距离为3,则点的坐标为(3,﹣2),
故答案为:(3,﹣2).
13.解:∵△DFE是由△DCE折叠得到的,
∴∠DEC=∠FED,
又∵∠EFB=45°,∠B=90°,
∴∠BEF=45°,
∴∠DEC=(180°﹣45°)=67.5°.
故答案为:67.5.
14.解:去括号,得:4x﹣7<5x﹣5,
移项,得:4x﹣5x<﹣5+7,
合并同类项,得:﹣x<2,
系数化为1,得:x>﹣2,
故答案为:x>﹣2.
15.解:由题意知道:题目中的数据可以整理为:(﹣1)1,(﹣1)2,…(﹣1)n,
∴第19个答案为:(﹣1)19=﹣3.
故答案为:﹣3.
16.解:∵AB⊥CD,
∴∠1+∠2=90°,
又∵∠2=2∠1,
∴3∠1=90°,
∴∠1=30°,
∴∠3=∠1=30°,
故答案为:30.
三.解答题(共4小题,满分28分,每小题7分)
17.解:原式=2+﹣1=3﹣1.
18.解:,
把①代入②得:5x+2x﹣3=11,即x=2,
把x=2代入①得:y=1,
则方程组的解为;.
19.解:,
由①得x≥3,
由②得x<5,
故此不等式组的解集为3≤x<5,
把解集表示在数轴为
20.解:(1)因为∠AOB=169°,∠AOC=∠BOD=90°,
所以∠BOC=∠AOB﹣∠AOC=169°﹣90°=79°,
所以∠COD=∠BOD﹣∠BOC=90°﹣79°=11°;
(2)∠AOD=∠BOC,理由:
因为∠AOC=∠BOD=90°,
所以∠AOD+∠DOC=90°,∠BOC+∠DOC=90°
所以∠AOD=∠BOC.
(3)存在,仍然有∠AOD=∠BOC.理由:
因为∠AOD=∠AOC﹣∠DOC,∠BOC=∠BOD﹣∠DOC.
又因为∠AOC=∠BOD=α,
所以∠AOD=∠BOC.
四.解答题(共3小题,满分24分,每小题8分)
21.解:(1)本次抽查的学生有:22÷0.11=200(人),
a=200×0.3=60,b=42÷200=0.21,
故答案为:60,0.21;
(2)由(1)知,a=60,
补全的频数分布直方图如右图所示;
(3)2400×(0.3+0.05)
=2400×0.35
=840(人),
答:该校学生视力达到4.9及以上的学生共约有840人.
22.解:①如图,△A1B1C1即为所求作,A1(0,﹣3),B1(5,﹣1),C1(3,2).
②由平移的性质可知,M(1,5),MM1=PP1,
故答案为:(1,5),MM1=PP1.
③=5×5﹣×5×3﹣×2×3﹣×5×2=9.5.
23.解:(1)设购买1个温馨提示牌需要x元,购买1个垃圾箱需要y元,
依题意,得:,
解得:.
答:购买1个温馨提示牌需要60元,购买1个垃圾箱需要120元.
(2)设购买m个垃圾箱,则购买(80﹣m)个温馨提示牌,
依题意,得:60(80﹣m)+120m≤8000,
解得:m≤.
又∵m为正整数,
∴m的最大值为53.
答:最多可以购买垃圾箱53个.
一.选择题(共10小题,满分30分,每小题3分)
1.下列各数:﹣1,,1.1212212221…(每两个1之间增加1个2),﹣3.1415,,﹣0.,其中无理数有( )
A.1个
B.2个
C.3个
D.4个
2.下面调查统计中,适合采用普查方式的是( )
A.华为手机的市场占有率
B.乘坐飞机的旅客是否携带了违禁物品
C.国家宝藏”专栏电视节目的收视率
D.“现代”汽车每百公里的耗油量
3.已知a>b,则在下列结论中,错误的是( )
A.a+2>b+2
B.﹣a<﹣b
C.a﹣3>b﹣3
D.1﹣2a>1﹣2b
4.已知方程mx+2y=﹣2,当x=3时y=5,那么m为( )
A.
B.﹣
C.﹣4
D.
5.如果不等式(a﹣3)x>a﹣3的解集是x<1,那么a的取值范围是( )
A.a>0
B.a<0
C.a>3
D.a<3
6.下列选项中,可以用来证明命题“若a>b,则|a|>|b|”是假命题的反例是( )
A.a=1,b=0
B.a=1,b=﹣2
C.a=﹣2,b=1
D.a=2,b=﹣1
7.如图所示,OB⊥OD,OC⊥OA,∠BOC=32°,那么∠AOD等于( )
A.148°
B.132°
C.128°
D.90°
8.如图,△ABC顶点C的坐标是(﹣3,2),过点C作AB上的高线CD,则垂足D点的坐标为( )
A.(2,0)
B.(﹣3,0)
C.(0,2)
D.(0,﹣3)
9.在抗击疫情网络知识竞赛中,为奖励成绩突出的学生,学校计划用200元钱购买A、B、C三种奖品,A种每个10元,B种每个20元,C种每个30元,在C种奖品不超过两个且钱全部用完的情况下,有多少种购买方案( )
A.12种
B.15种
C.16种
D.14种
10.如图,下列条件:①∠1=∠2,②∠3+∠4=180°,③∠5+∠6=180°,④∠2=∠3,⑤∠7=∠2+∠3,⑥∠7+∠4﹣∠1=180°中能判断直线a∥b的有( )
A.3个
B.4个
C.5个
D.6个
二.填空题(共6小题,满分18分,每小题3分)
11.有一个数值转换器,原理如图所示,当输入的x为512时,输出的y是
.
12.在平面直角坐标系xOy中,点P在第四象限内,且点P到x轴的距离是2,到y轴的距离是3,则点P的坐标是
.
13.如图,将长方形ABCD沿DE折叠,使点C落在边AB上的点F处,若∠EFB=45°,则∠DEC=
°.
14.不等式4x﹣7<5(x﹣1)的解集是
.
15.观察分析下列数据:0,,,3,,,,…,根据数据排列的规律得到第19个数据应是
.
16.如图,直线AB⊥CD,EF经过点O,∠2=2∠1,则∠3=
°.
三.解答题(共4小题,满分28分,每小题7分)
17.计算:
+|﹣1|.
18.解方程组:
19.解不等式组,并把解集表示在数轴上.
20.如图,射线OC、OD在∠AOB的内部.
(1)∠AOB=169°,∠AOC=∠BOD=90°,求∠COD的度数.
(2)当∠AOC=∠BOD=90°,试判断∠AOD与∠BOC的关系,说明理由.
(3)当∠AOC=∠BOD=α,(2)中的结论还存在吗?为什么?
四.解答题(共3小题,满分24分,每小题8分)
21.某校为了解全校2400名学生的视力情况,进行了一次视力抽样调查,并将调查所得的数据整理如下.
视力
频数/人
频率
4.0≤x<4.3
22
0.11
4.3≤x<4.6
42
b
4.6≤x<4.9
66
0.33
4.9≤x<5.2
a
0.3
5.2≤x<5.5
10
0.05
根据以上图表信息,解答下列问题:
(1)表中的a=
,b=
.
(2)请在答题卡上把频数分布直方图补充完整.(画图后请标注相应的数据)
(3)该校学生视力达到4.9及以上的学生共约有多少人?
22.在如图所示的直角坐标系中,△ABC的顶点坐标分别是A(﹣4,﹣1),B(1,1),C(﹣1,4);点P(x1,y1)是△ABC内一点,当点P(x1,y1)平移到点P1(x1+4,y1﹣2)时.
①请画出平移后新△A1B1C1,并直接写出△A1B1C1三个顶点的坐标;
②若三角形ABC外有一点M经过同样的平移后得到点M1(5,3),则M点的坐标是
.若连接线段MM1,PP1,则这两条线段之间的关系是
.
③求△A1B1C1的面积.
23.为了更好地提高业主垃圾分类的意识,某小区物业管理委员会决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和2个垃圾箱共需要420元,且每个温馨提示牌比垃圾箱便宜60元.
(1)问购买1个温馨提示牌和1个垃圾箱各需要多少元?
(2)如果需要购买温馨提示牌和垃圾箱共80个,且费用不超过8000元,问最多可以购买垃圾箱多少个?
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:﹣1是整数,属于有理数;
﹣3.1415是有限小数,属于有理数;
是分数,属于有理数;
﹣0.是循环小数,属于有理数;
无理数有,1.1212212221…(每两个1之间增加1个2)共2个.
故选:B.
2.解:A、对华为手机的市场占有率的调查范围广,适合抽样调查,故此选项不符合题意;
B、对乘坐飞机的旅客是否携带了违禁物品的调查情况适合普查,故此选项符合题意;
C、对国家宝藏”专栏电视节目的收视率的调查范围广,适合抽样调查,故此选项不符合题意;
D、对“现代”汽车每百公里的耗油量的调查范围广适合抽样调查,故此选项不符合题意;
故选:B.
3.解:A、∵a>b,∴a+2>b+2,故A正确,不符合题意.
B、∵a>b,∵﹣a<﹣b.故B正确,不符合题意.
C、∵a>b,∴a﹣3>b﹣3,故C正确,不符合题意.
D、∵a>b,∴﹣2a<﹣2b,∴1﹣2a<1﹣2b.故D错误,符合题意.
故选:D.
4.解:把x=3,y=5代入方程得:3m+10=﹣2,
移项合并得:3m=﹣12,
解得:m=﹣4,
故选:C.
5.解:∵(a﹣3)x>a﹣3的解集是x<1,
∴a﹣3<0,
解得a<3,
故选:D.
6.解:当a=1,b=﹣2时,a>b,但|a|<|b|,
故选:B.
7.解:∵OB⊥OD,所以∠BOD=90°
∵OC⊥OA
∴∠AOC=90°
∴∠AOB=∠AOC﹣∠BOC=90°﹣32°=58°
∴∠AOD=∠AOB+∠BOD=90°+58°=148°
故选:A.
8.解:过点C作CD垂直于x轴,垂足为D,
∵点C(﹣3,2),
∴点D横坐标与点C横坐标相等,
∴点D(﹣3,0).
故选:B.
9.解:设购买A种奖品m个,购买B种奖品n个,
当C种奖品个数为1个时,
根据题意得10m+20n+30=200,
整理得m+2n=17,
∵m、n都是正整数,0<2n<17,
∴n=1,2,3,4,5,6,7,8;
当C种奖品个数为2个时,
根据题意得10m+20n+60=200,
整理得m+2n=14,
∵m、n都是正整数,0<2n<14,
∴n=1,2,3,4,5,6;
∴有8+6=14种购买方案.
故选:D.
10.解:①由∠1=∠2,可得a∥b;
②由∠3+∠4=180°,可得a∥b;
③由∠5+∠6=180°,∠3+∠6=180°,可得∠5=∠3,即可得到a∥b;
④由∠2=∠3,不能得到a∥b;
⑤由∠7=∠2+∠3,∠7=∠1+∠3可得∠1=∠2,即可得到a∥b;
⑥由∠7+∠4﹣∠1=180°,∠7﹣∠1=∠3,可得∠3+∠4=180°,即可得到a∥b;
故选:C.
二.填空题(共6小题,满分18分,每小题3分)
11.解:由题中所给的程序可知:把512取立方根,结果为8,
因为8是有理数,所以再取立方根为2,
2是有理数,所以再取立方根为,
因为是无理数,输出,
故答案为:.
12.解:若点P在第四象限,且点P到x轴的距离为2,到y轴的距离为3,则点的坐标为(3,﹣2),
故答案为:(3,﹣2).
13.解:∵△DFE是由△DCE折叠得到的,
∴∠DEC=∠FED,
又∵∠EFB=45°,∠B=90°,
∴∠BEF=45°,
∴∠DEC=(180°﹣45°)=67.5°.
故答案为:67.5.
14.解:去括号,得:4x﹣7<5x﹣5,
移项,得:4x﹣5x<﹣5+7,
合并同类项,得:﹣x<2,
系数化为1,得:x>﹣2,
故答案为:x>﹣2.
15.解:由题意知道:题目中的数据可以整理为:(﹣1)1,(﹣1)2,…(﹣1)n,
∴第19个答案为:(﹣1)19=﹣3.
故答案为:﹣3.
16.解:∵AB⊥CD,
∴∠1+∠2=90°,
又∵∠2=2∠1,
∴3∠1=90°,
∴∠1=30°,
∴∠3=∠1=30°,
故答案为:30.
三.解答题(共4小题,满分28分,每小题7分)
17.解:原式=2+﹣1=3﹣1.
18.解:,
把①代入②得:5x+2x﹣3=11,即x=2,
把x=2代入①得:y=1,
则方程组的解为;.
19.解:,
由①得x≥3,
由②得x<5,
故此不等式组的解集为3≤x<5,
把解集表示在数轴为
20.解:(1)因为∠AOB=169°,∠AOC=∠BOD=90°,
所以∠BOC=∠AOB﹣∠AOC=169°﹣90°=79°,
所以∠COD=∠BOD﹣∠BOC=90°﹣79°=11°;
(2)∠AOD=∠BOC,理由:
因为∠AOC=∠BOD=90°,
所以∠AOD+∠DOC=90°,∠BOC+∠DOC=90°
所以∠AOD=∠BOC.
(3)存在,仍然有∠AOD=∠BOC.理由:
因为∠AOD=∠AOC﹣∠DOC,∠BOC=∠BOD﹣∠DOC.
又因为∠AOC=∠BOD=α,
所以∠AOD=∠BOC.
四.解答题(共3小题,满分24分,每小题8分)
21.解:(1)本次抽查的学生有:22÷0.11=200(人),
a=200×0.3=60,b=42÷200=0.21,
故答案为:60,0.21;
(2)由(1)知,a=60,
补全的频数分布直方图如右图所示;
(3)2400×(0.3+0.05)
=2400×0.35
=840(人),
答:该校学生视力达到4.9及以上的学生共约有840人.
22.解:①如图,△A1B1C1即为所求作,A1(0,﹣3),B1(5,﹣1),C1(3,2).
②由平移的性质可知,M(1,5),MM1=PP1,
故答案为:(1,5),MM1=PP1.
③=5×5﹣×5×3﹣×2×3﹣×5×2=9.5.
23.解:(1)设购买1个温馨提示牌需要x元,购买1个垃圾箱需要y元,
依题意,得:,
解得:.
答:购买1个温馨提示牌需要60元,购买1个垃圾箱需要120元.
(2)设购买m个垃圾箱,则购买(80﹣m)个温馨提示牌,
依题意,得:60(80﹣m)+120m≤8000,
解得:m≤.
又∵m为正整数,
∴m的最大值为53.
答:最多可以购买垃圾箱53个.
同课章节目录
