三年级数学下册搭配(二)同步练习(含答案)人教版
文档属性
| 名称 | 三年级数学下册搭配(二)同步练习(含答案)人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 385.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 21:03:43 | ||
图片预览




文档简介
三年级数学下册搭配(二)同步练习(含答案)人教版
一、填空题
1.两件上衣和3条裤子一共有(________)种穿法。
2.用0、2、5、8能组成(________)个没有重复数字的两位数,其中最大的是(________),最小的是(________)。
3.刘梅去郊游,她有三件上衣和四条裤子,刘梅共有(________)种不同的搭配方案。
4.甲、乙、丙、丁四个同学,每两个人握一次手,一共要握(________)次手。
5.用0、1、5、7可以组成(________)个没有重复的两位数。
6.从1~12中选出7个自然数,要求选出的数中不存在某个自然数是另一个自然数的2倍,那么一共有(______)种选法。
7.从false到false这false个自然数中有(______)个数的各位数字之和能被4整除。
8.如图,将1,2,3,4,5分别填入图中false的格子中,要求填在黑格里的数比它旁边的两个数都大。共有(______)种不同的填法。
9.从1到20中,最多能取______个数,使任意两个数不是3倍关系。
10.从1,2,3,4,5,6中选取若干个数,使得它们的和是3的倍数,但不是5的倍数。那么共有(______)种不同的选取方法。
11.在下图的每个区域内涂上false、false、false、false四种颜色之一,使得每个圆里面恰有四种颜色,则一共有__________种不同的染色方法。
12.如图,27个单位正方体拼成大正方体,沿着面上的格线,从A到B的最短路线共有(______)条。
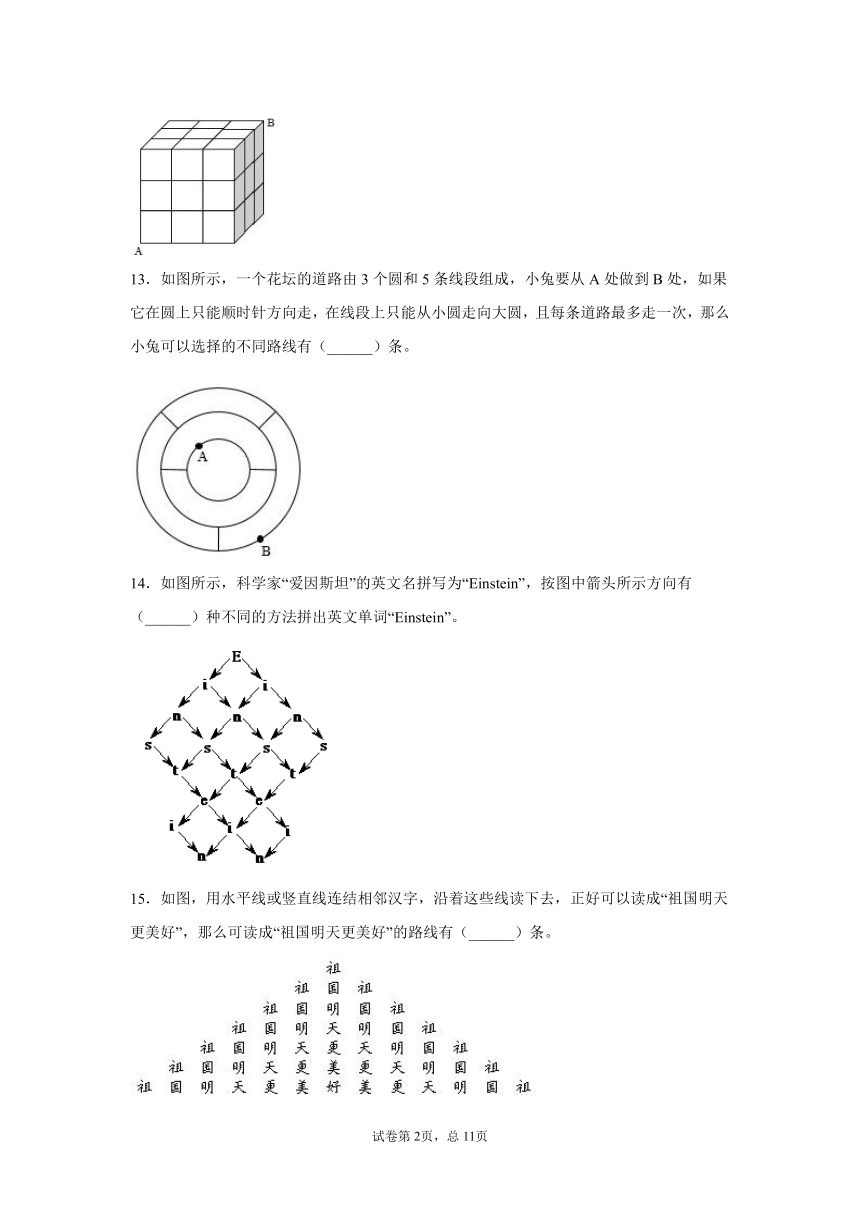
13.如图所示,一个花坛的道路由3个圆和5条线段组成,小兔要从A处做到B处,如果它在圆上只能顺时针方向走,在线段上只能从小圆走向大圆,且每条道路最多走一次,那么小兔可以选择的不同路线有(______)条。
14.如图所示,科学家“爱因斯坦”的英文名拼写为“Einstein”,按图中箭头所示方向有(______)种不同的方法拼出英文单词“Einstein”。
15.如图,用水平线或竖直线连结相邻汉字,沿着这些线读下去,正好可以读成“祖国明天更美好”,那么可读成“祖国明天更美好”的路线有(______)条。
二、选择题
1.姐姐有3件上衣和2条裤子,共有( )种不同的穿法。
A.2 B.4 C.6
2.张红有3件上衣和4条裙子,她共有( )种不同的搭配方案。
A.3 B.7 C.12
3.用0、4、8可以组成( )个不同的两位数。
A.4 B.5 C.6
4.按照中国篮球职业联赛组委会的规定,各队队员的号码可以选择的范围是0~55号,但选择两位数的号码时,每位数字均不能超过5,那么,可供每支球队选择的号码共( )个。
A.34 B.35 C.40 D.56
5.3个人握手,每两个人握1次手,共握( )次。
A.3 B.4 C.6
6.把四张扑克牌(如下图)反扣在桌面上,任意摸2张,可能有( )种不同的情况。
A.4 B.5 C.6 D.7
7.有24支篮球队参加比赛,比赛实行单场淘汰制,即每场比赛淘汰一支球队。一共要进行( )场比赛才能产生冠军。
A.23 B.24 C.25
8.妈妈用两件上衣和四条裤子,能有( )种不同的搭配选择。
A.4 B.8 C.16
9.学校进行乒乓球选拔赛,每个参赛选手都要和其他所有选手各赛一场,一共进行了false场比赛,有( )人参加了选拔赛。
A.false B.false C.false
10.把5件相同的礼物全部分给3个小朋友,使每个小朋友都分到礼物,分礼物的不同方法一共有( )种。
A.3 B.4 C.5 D.6
三、判断题
1.用1、2、3、4能组成12个没有重复数字的两位数,其中最大的两位数是43。(________)
2.2件上衣和3件下衣,每次上衣和下衣只能各穿1件,一共有5种穿法。(________)
3.小王用2件上衣和3条裤子,能搭配出9套衣服。(________)
4.六一儿童节快到了,三个小朋友中,每两个互相用微信发1条消息问好,一共发了6条信息。(________)
四、作图题
用一顶帽子配一条围巾,一共有false(种)搭配方法。请你在下图中表示出“4”的意义。
五、解答题
1.有两个骰子,每个骰子的六个面分别有1、2、3、4、5、6个点。随意掷这两个骰子,向上一面点数之和为偶数的情形有多少种?
2.从7,8,9,false,76,77这71个数中,选取两个不同的数,使其和为3的倍数的选法总数是多少?
3.从自然数1~40中任意选取两个数,使得所选取的两个数的和能被4整除,有多少种取法?
4.七位数的各位数字之和为60,这样的七位数一共有多少个?
5.用6种不同的颜色来涂正方体的六个面,使得不同的面涂上不同的颜色一共有多少种涂色的方法?(将正方体任意旋转之后仍然不同的涂色方法才被认为是相同的)
6.一种食物搭配一种饮料,一共有多少种不同的搭配?最便宜的一种需要多少钱?
食物价格表
饮料价格表
鸡腿堡:8.6元/个
虾堡:9.3元/个
可乐:5.6元/瓶
雪碧:5.2元/瓶
矿泉水:2.5元/瓶
果汁:6.3元/杯
参考答案
1.6
【解答】从2件上衣中选一件有2种选法;从3条裤子中选一条有3种选法;要配成一套衣服,根据乘法原理可得,共有:3×2=6种不同的搭配方法,据此解答即可。
2.9 85 20
【解答】组成两位数,十位为2时,有:20、25、28;
十位为5时,有:50、52、58;
十位为8时,有:80、82、85;
3.12
【解答】从三件上衣中选一件有3种选法;从四条裤子中选一条有4种选法;根据乘法原理,可得共有:3×4=12(种);据此解答。
4.6
【解答】每个人都要和另外的3个人握一次手,4个人共握4×3=12次,由于每两人握手,应算作握一次手,去掉重复的情况,实际只握了12÷2=6次,据此解答。
5.9
【解答】0不能在最高位上,则十位上是1时,可组成10、15、17;十位上是5时,可组成50、51、57;十位上是7时,可组成70、71、75。
6.47
【解答】由于要求选出的数中不存在某个自然数是另一个自然数的2倍,可以先根据2倍关系将1~12进行如下分组:(1,2,4,8);(3,4,12);(5,10);(7);(9);(11)。
7.248
【解答】由于在一个数的前面写上几个0不影响这个数的各位数字之和,所以可以将1到999中的一位数和两位数的前面补上两个或一个0,使之成为一个三位数。现在相当于要求001到999中各位数字之和能被4整除的数的个数。一个数除以4的余数可能为0,1,2,3,0~9中除以4余0的数有3个,除以4余1的也有3个,除以4余2和3的各有2个。三个数的和要能被4整除,必须要求它们除以4的余数的和能被4整除,余数的情况有如下5种:0+0+0;0+1+3;0+2+2;1+1+2;2+3+3。
8.16
【解答】因为要求“填在黑格里的数比它旁边的两个数都大”,所以填入黑格中的数不能够太小,否则就不满足条件。通过枚举法可知填入黑格里的数只有两类:第一类,填在黑格里的数是5和4;第二类,填在黑格里的数是5和3.接下来就根据这两类进行计数:
9.16
【解答】先找出1到20中,存在3倍关系的数的组合,然后考虑如何去掉一些数,使得任意两个数不是3倍关系。
10.false
【解答】从1~6这些数中选取的数的和小于21,满足条件的和数有3、6、9、12、18、21,分别求出每一种情况的个数,相加得到总数。
11.24
【解答】每个圆都被分成4块,可以先取其中一个研究,先确定这个圆的染色方法,然后考虑其它3块的染色方法。
12.384
【解答】从A到B的最短路线,典型的标数法问题,但这里是在立体图形中,与平面图形的标数法略有不同。如图所示:
128+ 128+128=384(条) 所以最短路线有条384条。
13.6
【解答】在线段上只能从小圆走向大圆,且每条道路最多走一次,也就是求最短路径的问题,用标数法求解。采用标数法,如图所示:
所以不同路线共有6条。
14.60
【解答】根据英文“Einstein”的字母顺序,确定false的标数顺序,从上往下依次标数即可。如图所示:
共有false(种)不同拼法。
15.127
【解答】必须按照“祖国明天更美好”往下读,典型的标数问题,按照祖→国→明→天→更→美→好的顺序进行标数即可。
如图所示:
所以可读成“祖国明天更美好”的路线有127条。
二、
1.C
【解答】假设三件上衣为A、B、C。裤子为E、F
当上衣选A时,裤子可选:AE、AF;
当上衣选B时,裤子可选:BE、BF;
当上衣选C时,裤子可选:CE、CF;
2.C
【解答】从4条裙子中选一条有4种选法、从3件上衣中选一件有3种选法,根据乘法原理可得,共有4×3=12种不同的搭配方案;据此解答即可。
3.A
【解答】0不能在最高位上,则十位上是4时,可组成48、40;十位上是8时,可组成84、80。
4.C
【解答】根据题意,可供选择的号码可以分为一位数和两位数两大类,一位数总共有10个,两位数要求每位数字均不能超过5,那么可以选择0、1、2、3、4、5,考虑到首位不为0,那么十位数字5种选法,个位数字6种选法。
5.A
【解答】3个人互相握手,每个人都要和其他两人握手,一共有6次,因为两人之间互相握一次即可,所以一共只需要握3次。
6.C
【解答】
7.A
【解答】淘汰赛每赛一场就要淘汰一支队伍,而且只能淘汰一支队伍。即淘汰掉多少支队伍就恰好进行了多少场比赛,由此解答即可。
8.B
【解答】妈妈的第1件上衣可以搭配4条裤子,有4种不同的搭配选择;妈妈的第2件上衣可以搭配4条裤子,有4种不同的搭配选择,共有4+4=8(种)不同的搭配选择。
9.B
【解答】每个参赛选手都要和其他所有选手各赛一场,符合单循环比赛的赛制,设有n个人参赛,那么总的比赛场次为false。
10.D
【解答】5分成3份,有两种分法,2、2、1或3、1、1,此题就可以按搭配方法,将两种分法进行搭配,数出总方法即可。
三、
1.√
【解答】分两步完成,第一步十位上的数字有4种不同的选择方法,余下的3个数字放在个位有3种选择,根据乘法原理有4×3=12个不同的两位数;其中最大的两位数,最高位是最大的数字4,个位是第二大的数字3,即43;据此解答即可。
2.×
【解答】根据题意可知,每件上衣都可以与3件下衣搭配,所以有3种穿法;每条下衣都可以与2件上衣搭配,所以有2种穿法。则2件上衣搭配3件下衣一共就有3×2种不同的穿法;据此解答即可。
3.×
【解答】小王的第一件上衣,分别搭配3条裤子,有三种搭配方法;第2件上衣分别搭配3条裤子也有3种搭配方法,把两类数相加即可解答。
4.√
【解答】每人需要发2条消息,用人数×每人发的消息数即可。
四、
【解答】根据题意可知,每顶帽子都可以与2条裙子搭配,所以有2种搭配方法;每条围巾都可以与4顶帽子搭配,所以有4种搭配方法。则4顶帽子搭配2条围巾一共就有4×2种不同的穿法。
或
五、
1.false种
【解答】可以分为两步:第一步第一个骰子随意掷有6种可能的点数;
第二步当第一个骰子的点数确定了以后,第二个骰子的点数只能是与第一个骰子的点数相同奇偶性的3种可能的点数。
根据乘法原理,向上一面的点数之和为偶数的情形有false(种)
答:向上一面点数之和为偶数的情形有18种。
2.829个
【解答】这71个数中被3整除,被3除余1,被3除余2的数分别有23、24、24个;
选取两个数只要是符合之前所说的两种情况就可以了,选取两个被3整除的数的方法有false种;
从被3除余1和被3除余2的数中各取1个的方法共有false种;
所以一共有false种选取方法。
答:和为3的倍数的选法总数是829个。
3.false种
【解答】第一类:余数分别为0,0。
1~40中能被4整除的数共有false(个),10个中选2个,有false(种)取法;
第二类:余数分别为1,3。
1~40中被4除余1,余3的数也分别都有10个,有false(种)取法;
第三类:余数分别为2,2。
同第一类,有45种取法。
根据加法原理,共有false(种)取法。
答:有190种取法。
4.false个
【解答】七位数数字之和最多可以为false。false。七位数的可能数字组合为:
①9,9,9,9,9,9,6。
第一种情况只需要确定6的位置即可。所以有6种情况。
②9,9,9,9,9,8,7。
第二种情况只需要确定8和7的位置,数字即确定。8有7个位置,7有6个位置。所以第二种情况可以组成的7位数有false个。
③9,9,9,9,8,8,8,
第三种情况,3个8的位置确定即7位数也确定。三个8的位置放置共有false种。
三个相同的8放置会产生false种重复的放置方式。
所以3个8和4个9组成的不同的七位数共有false种。
所以数字和为60的七位数共有false。
答:这样的七位数一共有84个。
5.30种
【解答】正方体6个面不同的涂色方法共有false种;
固定一个底面共有6种不同的选法,选择一个与底面相邻的面有4种不同的选法。所以一个正方体的放置有false种不同的位置。
即在旋转的时候可以重复24次。所以可以染色的不同方法共有false(种)。
答:一共有30种涂色的方法。
6.8种;11.1元
【解答】4×2=8(种)
饮料:6.3>5.6>5.2>2.5
食物:9.3>8.6
2.5+8.6=11.1(元)
答:一共有8种不同的搭配;最便宜的一种需要11.1元。
一、填空题
1.两件上衣和3条裤子一共有(________)种穿法。
2.用0、2、5、8能组成(________)个没有重复数字的两位数,其中最大的是(________),最小的是(________)。
3.刘梅去郊游,她有三件上衣和四条裤子,刘梅共有(________)种不同的搭配方案。
4.甲、乙、丙、丁四个同学,每两个人握一次手,一共要握(________)次手。
5.用0、1、5、7可以组成(________)个没有重复的两位数。
6.从1~12中选出7个自然数,要求选出的数中不存在某个自然数是另一个自然数的2倍,那么一共有(______)种选法。
7.从false到false这false个自然数中有(______)个数的各位数字之和能被4整除。
8.如图,将1,2,3,4,5分别填入图中false的格子中,要求填在黑格里的数比它旁边的两个数都大。共有(______)种不同的填法。
9.从1到20中,最多能取______个数,使任意两个数不是3倍关系。
10.从1,2,3,4,5,6中选取若干个数,使得它们的和是3的倍数,但不是5的倍数。那么共有(______)种不同的选取方法。
11.在下图的每个区域内涂上false、false、false、false四种颜色之一,使得每个圆里面恰有四种颜色,则一共有__________种不同的染色方法。
12.如图,27个单位正方体拼成大正方体,沿着面上的格线,从A到B的最短路线共有(______)条。
13.如图所示,一个花坛的道路由3个圆和5条线段组成,小兔要从A处做到B处,如果它在圆上只能顺时针方向走,在线段上只能从小圆走向大圆,且每条道路最多走一次,那么小兔可以选择的不同路线有(______)条。
14.如图所示,科学家“爱因斯坦”的英文名拼写为“Einstein”,按图中箭头所示方向有(______)种不同的方法拼出英文单词“Einstein”。
15.如图,用水平线或竖直线连结相邻汉字,沿着这些线读下去,正好可以读成“祖国明天更美好”,那么可读成“祖国明天更美好”的路线有(______)条。
二、选择题
1.姐姐有3件上衣和2条裤子,共有( )种不同的穿法。
A.2 B.4 C.6
2.张红有3件上衣和4条裙子,她共有( )种不同的搭配方案。
A.3 B.7 C.12
3.用0、4、8可以组成( )个不同的两位数。
A.4 B.5 C.6
4.按照中国篮球职业联赛组委会的规定,各队队员的号码可以选择的范围是0~55号,但选择两位数的号码时,每位数字均不能超过5,那么,可供每支球队选择的号码共( )个。
A.34 B.35 C.40 D.56
5.3个人握手,每两个人握1次手,共握( )次。
A.3 B.4 C.6
6.把四张扑克牌(如下图)反扣在桌面上,任意摸2张,可能有( )种不同的情况。
A.4 B.5 C.6 D.7
7.有24支篮球队参加比赛,比赛实行单场淘汰制,即每场比赛淘汰一支球队。一共要进行( )场比赛才能产生冠军。
A.23 B.24 C.25
8.妈妈用两件上衣和四条裤子,能有( )种不同的搭配选择。
A.4 B.8 C.16
9.学校进行乒乓球选拔赛,每个参赛选手都要和其他所有选手各赛一场,一共进行了false场比赛,有( )人参加了选拔赛。
A.false B.false C.false
10.把5件相同的礼物全部分给3个小朋友,使每个小朋友都分到礼物,分礼物的不同方法一共有( )种。
A.3 B.4 C.5 D.6
三、判断题
1.用1、2、3、4能组成12个没有重复数字的两位数,其中最大的两位数是43。(________)
2.2件上衣和3件下衣,每次上衣和下衣只能各穿1件,一共有5种穿法。(________)
3.小王用2件上衣和3条裤子,能搭配出9套衣服。(________)
4.六一儿童节快到了,三个小朋友中,每两个互相用微信发1条消息问好,一共发了6条信息。(________)
四、作图题
用一顶帽子配一条围巾,一共有false(种)搭配方法。请你在下图中表示出“4”的意义。
五、解答题
1.有两个骰子,每个骰子的六个面分别有1、2、3、4、5、6个点。随意掷这两个骰子,向上一面点数之和为偶数的情形有多少种?
2.从7,8,9,false,76,77这71个数中,选取两个不同的数,使其和为3的倍数的选法总数是多少?
3.从自然数1~40中任意选取两个数,使得所选取的两个数的和能被4整除,有多少种取法?
4.七位数的各位数字之和为60,这样的七位数一共有多少个?
5.用6种不同的颜色来涂正方体的六个面,使得不同的面涂上不同的颜色一共有多少种涂色的方法?(将正方体任意旋转之后仍然不同的涂色方法才被认为是相同的)
6.一种食物搭配一种饮料,一共有多少种不同的搭配?最便宜的一种需要多少钱?
食物价格表
饮料价格表
鸡腿堡:8.6元/个
虾堡:9.3元/个
可乐:5.6元/瓶
雪碧:5.2元/瓶
矿泉水:2.5元/瓶
果汁:6.3元/杯
参考答案
1.6
【解答】从2件上衣中选一件有2种选法;从3条裤子中选一条有3种选法;要配成一套衣服,根据乘法原理可得,共有:3×2=6种不同的搭配方法,据此解答即可。
2.9 85 20
【解答】组成两位数,十位为2时,有:20、25、28;
十位为5时,有:50、52、58;
十位为8时,有:80、82、85;
3.12
【解答】从三件上衣中选一件有3种选法;从四条裤子中选一条有4种选法;根据乘法原理,可得共有:3×4=12(种);据此解答。
4.6
【解答】每个人都要和另外的3个人握一次手,4个人共握4×3=12次,由于每两人握手,应算作握一次手,去掉重复的情况,实际只握了12÷2=6次,据此解答。
5.9
【解答】0不能在最高位上,则十位上是1时,可组成10、15、17;十位上是5时,可组成50、51、57;十位上是7时,可组成70、71、75。
6.47
【解答】由于要求选出的数中不存在某个自然数是另一个自然数的2倍,可以先根据2倍关系将1~12进行如下分组:(1,2,4,8);(3,4,12);(5,10);(7);(9);(11)。
7.248
【解答】由于在一个数的前面写上几个0不影响这个数的各位数字之和,所以可以将1到999中的一位数和两位数的前面补上两个或一个0,使之成为一个三位数。现在相当于要求001到999中各位数字之和能被4整除的数的个数。一个数除以4的余数可能为0,1,2,3,0~9中除以4余0的数有3个,除以4余1的也有3个,除以4余2和3的各有2个。三个数的和要能被4整除,必须要求它们除以4的余数的和能被4整除,余数的情况有如下5种:0+0+0;0+1+3;0+2+2;1+1+2;2+3+3。
8.16
【解答】因为要求“填在黑格里的数比它旁边的两个数都大”,所以填入黑格中的数不能够太小,否则就不满足条件。通过枚举法可知填入黑格里的数只有两类:第一类,填在黑格里的数是5和4;第二类,填在黑格里的数是5和3.接下来就根据这两类进行计数:
9.16
【解答】先找出1到20中,存在3倍关系的数的组合,然后考虑如何去掉一些数,使得任意两个数不是3倍关系。
10.false
【解答】从1~6这些数中选取的数的和小于21,满足条件的和数有3、6、9、12、18、21,分别求出每一种情况的个数,相加得到总数。
11.24
【解答】每个圆都被分成4块,可以先取其中一个研究,先确定这个圆的染色方法,然后考虑其它3块的染色方法。
12.384
【解答】从A到B的最短路线,典型的标数法问题,但这里是在立体图形中,与平面图形的标数法略有不同。如图所示:
128+ 128+128=384(条) 所以最短路线有条384条。
13.6
【解答】在线段上只能从小圆走向大圆,且每条道路最多走一次,也就是求最短路径的问题,用标数法求解。采用标数法,如图所示:
所以不同路线共有6条。
14.60
【解答】根据英文“Einstein”的字母顺序,确定false的标数顺序,从上往下依次标数即可。如图所示:
共有false(种)不同拼法。
15.127
【解答】必须按照“祖国明天更美好”往下读,典型的标数问题,按照祖→国→明→天→更→美→好的顺序进行标数即可。
如图所示:
所以可读成“祖国明天更美好”的路线有127条。
二、
1.C
【解答】假设三件上衣为A、B、C。裤子为E、F
当上衣选A时,裤子可选:AE、AF;
当上衣选B时,裤子可选:BE、BF;
当上衣选C时,裤子可选:CE、CF;
2.C
【解答】从4条裙子中选一条有4种选法、从3件上衣中选一件有3种选法,根据乘法原理可得,共有4×3=12种不同的搭配方案;据此解答即可。
3.A
【解答】0不能在最高位上,则十位上是4时,可组成48、40;十位上是8时,可组成84、80。
4.C
【解答】根据题意,可供选择的号码可以分为一位数和两位数两大类,一位数总共有10个,两位数要求每位数字均不能超过5,那么可以选择0、1、2、3、4、5,考虑到首位不为0,那么十位数字5种选法,个位数字6种选法。
5.A
【解答】3个人互相握手,每个人都要和其他两人握手,一共有6次,因为两人之间互相握一次即可,所以一共只需要握3次。
6.C
【解答】
7.A
【解答】淘汰赛每赛一场就要淘汰一支队伍,而且只能淘汰一支队伍。即淘汰掉多少支队伍就恰好进行了多少场比赛,由此解答即可。
8.B
【解答】妈妈的第1件上衣可以搭配4条裤子,有4种不同的搭配选择;妈妈的第2件上衣可以搭配4条裤子,有4种不同的搭配选择,共有4+4=8(种)不同的搭配选择。
9.B
【解答】每个参赛选手都要和其他所有选手各赛一场,符合单循环比赛的赛制,设有n个人参赛,那么总的比赛场次为false。
10.D
【解答】5分成3份,有两种分法,2、2、1或3、1、1,此题就可以按搭配方法,将两种分法进行搭配,数出总方法即可。
三、
1.√
【解答】分两步完成,第一步十位上的数字有4种不同的选择方法,余下的3个数字放在个位有3种选择,根据乘法原理有4×3=12个不同的两位数;其中最大的两位数,最高位是最大的数字4,个位是第二大的数字3,即43;据此解答即可。
2.×
【解答】根据题意可知,每件上衣都可以与3件下衣搭配,所以有3种穿法;每条下衣都可以与2件上衣搭配,所以有2种穿法。则2件上衣搭配3件下衣一共就有3×2种不同的穿法;据此解答即可。
3.×
【解答】小王的第一件上衣,分别搭配3条裤子,有三种搭配方法;第2件上衣分别搭配3条裤子也有3种搭配方法,把两类数相加即可解答。
4.√
【解答】每人需要发2条消息,用人数×每人发的消息数即可。
四、
【解答】根据题意可知,每顶帽子都可以与2条裙子搭配,所以有2种搭配方法;每条围巾都可以与4顶帽子搭配,所以有4种搭配方法。则4顶帽子搭配2条围巾一共就有4×2种不同的穿法。
或
五、
1.false种
【解答】可以分为两步:第一步第一个骰子随意掷有6种可能的点数;
第二步当第一个骰子的点数确定了以后,第二个骰子的点数只能是与第一个骰子的点数相同奇偶性的3种可能的点数。
根据乘法原理,向上一面的点数之和为偶数的情形有false(种)
答:向上一面点数之和为偶数的情形有18种。
2.829个
【解答】这71个数中被3整除,被3除余1,被3除余2的数分别有23、24、24个;
选取两个数只要是符合之前所说的两种情况就可以了,选取两个被3整除的数的方法有false种;
从被3除余1和被3除余2的数中各取1个的方法共有false种;
所以一共有false种选取方法。
答:和为3的倍数的选法总数是829个。
3.false种
【解答】第一类:余数分别为0,0。
1~40中能被4整除的数共有false(个),10个中选2个,有false(种)取法;
第二类:余数分别为1,3。
1~40中被4除余1,余3的数也分别都有10个,有false(种)取法;
第三类:余数分别为2,2。
同第一类,有45种取法。
根据加法原理,共有false(种)取法。
答:有190种取法。
4.false个
【解答】七位数数字之和最多可以为false。false。七位数的可能数字组合为:
①9,9,9,9,9,9,6。
第一种情况只需要确定6的位置即可。所以有6种情况。
②9,9,9,9,9,8,7。
第二种情况只需要确定8和7的位置,数字即确定。8有7个位置,7有6个位置。所以第二种情况可以组成的7位数有false个。
③9,9,9,9,8,8,8,
第三种情况,3个8的位置确定即7位数也确定。三个8的位置放置共有false种。
三个相同的8放置会产生false种重复的放置方式。
所以3个8和4个9组成的不同的七位数共有false种。
所以数字和为60的七位数共有false。
答:这样的七位数一共有84个。
5.30种
【解答】正方体6个面不同的涂色方法共有false种;
固定一个底面共有6种不同的选法,选择一个与底面相邻的面有4种不同的选法。所以一个正方体的放置有false种不同的位置。
即在旋转的时候可以重复24次。所以可以染色的不同方法共有false(种)。
答:一共有30种涂色的方法。
6.8种;11.1元
【解答】4×2=8(种)
饮料:6.3>5.6>5.2>2.5
食物:9.3>8.6
2.5+8.6=11.1(元)
答:一共有8种不同的搭配;最便宜的一种需要11.1元。
