9.9 利用位似放缩图形同步练习(含答案)
文档属性
| 名称 | 9.9 利用位似放缩图形同步练习(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-25 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第九章 图形的相似
9 利用位似放缩图形
知识能力全练
知识点一 位似多边形的概念全
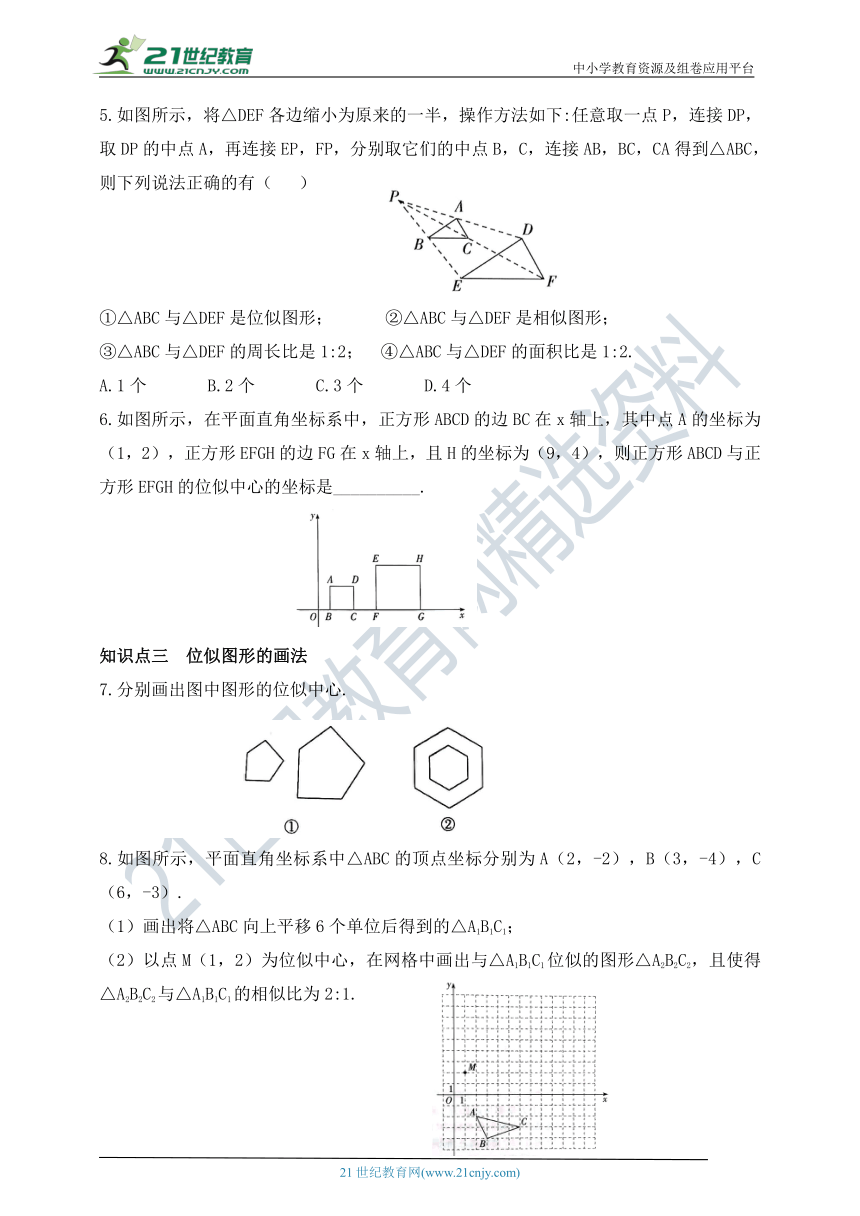
1.下列各组图形中,不是位似图形的为( )
2.如图所示,网格中的△ABC与△DEF是不是位似图形?如果不是,说明理由;如果是,请指出它们的位似中心.
知识点二 位似图形的性质全
3.如图所示,△ABC与△DEF是位似图形,相似比是1:2,已知DE=4,则AB的长是( )
A.2 B.4 C.8 D.1
4.如图所示,E、F、G、H分别是OA、OB、OC、OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )
A.6 B.9 C.12 D.18
5.如图所示,将△DEF各边缩小为原来的一半,操作方法如下:任意取一点P,连接DP,取DP的中点A,再连接EP,FP,分别取它们的中点B,C,连接AB,BC,CA得到△ABC,则下列说法正确的有( )
①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比是1:2; ④△ABC与△DEF的面积比是1:2.
A.1个 B.2个 C.3个 D.4个
6.如图所示,在平面直角坐标系中,正方形ABCD的边BC在x轴上,其中点A的坐标为(1,2),正方形EFGH的边FG在x轴上,且H的坐标为(9,4),则正方形ABCD与正方形EFGH的位似中心的坐标是__________.
知识点三 位似图形的画法
7.分别画出图中图形的位似中心.
8.如图所示,平面直角坐标系中△ABC的顶点坐标分别为A(2,-2),B(3,-4),C(6,-3).
(1)画出将△ABC向上平移6个单位后得到的△A1B1C1;
(2)以点M(1,2)为位似中心,在网格中画出与△A1B1C1位似的图形△A2B2C2,且使得△A2B2C2与△A1B1C1的相似比为2:1.
知识点四 平面直角坐标系中的位似变换
9.在平面直角坐标系中,点A,B的坐标分别是(4,2),B(5,0),以O为位似中心,相似比为1:2,把△ABO各边缩小,得到△A1B1O,则点A的对应点A1的坐标为( )
A.(2,1) B.(2,-1) C.(-2,-1) D.(2,1)或(-2,-1)
10.如图所示,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,且OA=8,OC=6,点B在第二象限,如果矩形OA'B'C'与矩形OABC关于点0位似,且矩形OA'B'C'的面积等于矩形OABC面积的,那么点B'的坐标是________.
11.如图所示,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4),以原点为位似中心,相似比为1:2,将△ABC各边缩小,则线段AC的中点P变换后对应点的坐标是__________.
12.如图所示,四边形ABCD是正方形,原点O是四边形ABCD和四边形A'B'C'D'的位似中心,点B、C的坐标分别为(-8,2),(-4,0),点B'是点B的对应点,且点B'的横坐标为-1,则四边形A'B'C'D'的周长为__________.
13.如图所示,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心在y轴左侧将△OBC各边放大为原来的两倍(即新图形与原图形的相似比为2),画出图形;
(2)如果△OBC内部一点M的坐标为(x,y),写出B、C、M对应点B',C',M'的坐标.
14.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,
相似比为,把△EFO各边缩小,则点E的对应点E'的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
15.如图所示,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO:AD=( )
A.2:3 B.2:5 C.4:9 D.4:13
16.如图所示,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=__________.
17.如图所示,以点O为位似中心,将五边形 ABCDE各边放大后得到五边形A'B'C'D'E',已知OA=10cm,OA'=20cm,则五边形 ABCDE的周长与五边形A'B'C'D'E'的周长的比是__________.
18.如图所示,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0)以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC各边放大到原来的2倍设点B的对应点B'的横坐标是a,则点B的横坐标是__________.
19.如图所示,网格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向下平移5格后得到△A1B1C1,写出点A1,B1,C1的坐标,并画出△A1B1C1;
(2)把△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2,写出点A2,B2,C2的坐标,并画出△A2B2C2;
(3)把△ABC各边以点O为位似中心放大得到△A3B3C3,使放大前后对应线段的比为1:2,写出点A3,B3,C3的坐标,并画出△A3B3C3.
20.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
21.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点O为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )
A. B.2 C.4 D.2
22.在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是___________.
23.如图所示,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为___________.
24.如图所示,△ABC中,三个顶点的坐标分别是A(-2,2),B(-4,1),C(-1,-1).以点C为位似中心,在x轴下方作△ABC的位似图形△A′B′C′,并把△ABC的边长放大为原来的2倍,那么点A的坐标为( )
A.(3,-7) B.(1,-7) C.(4,-4) D.(1,-4)
参考答案
1.B
2.解析 是位似图形.
如图,(1)对应点的连线交于同一点;
设每个小正方形的边长为1,则DF=,AC=2,DE=2,AB=4,EF=,BC=2,三边对应成比例,两个三角形相似。
综合(1)(2)知,它们是位似图形,位似中心为P.
3.A 4.C 5.C 6. (-3,0)或(,)
7.解析 画出两组对应点的连线,找出它们的交点,即是位似中心,如图,P,O即为所求的位似中心.
8.解析 (1)如图,△A1B1C1即为所作.
(2)如图,△A2B2C2即为所作.
9.D 10.(-4,3)或(4,-3) 11.(2,)或(-2,-) 12.
13.解析 (1)如图所示,△B'C'O即为所求.
(2)如图所示,∵B、C两点的坐标分别为3,-1),(2,1),新图形与原图形的相似比为2,∴B'(-6,2),C'(-4,-2).
∵△OBC内部一点M的坐标为(x,y),∴其对应点M的坐标为(-2x,-2y).
14.D 15.B 16. 4.5 17. 1:2 18.
19.解析(1)如图所示,△A1B1C1即为所求.
点A1,B1,C1的坐标分别为(3,-2),(-1,-6),(5,-6).
(2)如图所示,△A2B2C2即为所求.
点A2,B2,C2的坐标分别为(-3,-3),(1,1),(-5,1).
(3)如图所示,△A3B3C3和△A′3B′3C′3即为所求,
点A3,B3,C3的坐标分别为(6,6),(-2,-2),(10,-2)或(-6,-6),(2,2),(-10,2).
20.A 21.D 22.(4,8)或(-4,-8) 23.(-5,-1) 24.B
_21?????????è?????(www.21cnjy.com)_
第九章 图形的相似
9 利用位似放缩图形
知识能力全练
知识点一 位似多边形的概念全
1.下列各组图形中,不是位似图形的为( )
2.如图所示,网格中的△ABC与△DEF是不是位似图形?如果不是,说明理由;如果是,请指出它们的位似中心.
知识点二 位似图形的性质全
3.如图所示,△ABC与△DEF是位似图形,相似比是1:2,已知DE=4,则AB的长是( )
A.2 B.4 C.8 D.1
4.如图所示,E、F、G、H分别是OA、OB、OC、OD的中点,已知四边形EFGH的面积是3,则四边形ABCD的面积是( )
A.6 B.9 C.12 D.18
5.如图所示,将△DEF各边缩小为原来的一半,操作方法如下:任意取一点P,连接DP,取DP的中点A,再连接EP,FP,分别取它们的中点B,C,连接AB,BC,CA得到△ABC,则下列说法正确的有( )
①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比是1:2; ④△ABC与△DEF的面积比是1:2.
A.1个 B.2个 C.3个 D.4个
6.如图所示,在平面直角坐标系中,正方形ABCD的边BC在x轴上,其中点A的坐标为(1,2),正方形EFGH的边FG在x轴上,且H的坐标为(9,4),则正方形ABCD与正方形EFGH的位似中心的坐标是__________.
知识点三 位似图形的画法
7.分别画出图中图形的位似中心.
8.如图所示,平面直角坐标系中△ABC的顶点坐标分别为A(2,-2),B(3,-4),C(6,-3).
(1)画出将△ABC向上平移6个单位后得到的△A1B1C1;
(2)以点M(1,2)为位似中心,在网格中画出与△A1B1C1位似的图形△A2B2C2,且使得△A2B2C2与△A1B1C1的相似比为2:1.
知识点四 平面直角坐标系中的位似变换
9.在平面直角坐标系中,点A,B的坐标分别是(4,2),B(5,0),以O为位似中心,相似比为1:2,把△ABO各边缩小,得到△A1B1O,则点A的对应点A1的坐标为( )
A.(2,1) B.(2,-1) C.(-2,-1) D.(2,1)或(-2,-1)
10.如图所示,在平面直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,且OA=8,OC=6,点B在第二象限,如果矩形OA'B'C'与矩形OABC关于点0位似,且矩形OA'B'C'的面积等于矩形OABC面积的,那么点B'的坐标是________.
11.如图所示,△ABC三个顶点的坐标分别为A(2,2),B(4,0),C(6,4),以原点为位似中心,相似比为1:2,将△ABC各边缩小,则线段AC的中点P变换后对应点的坐标是__________.
12.如图所示,四边形ABCD是正方形,原点O是四边形ABCD和四边形A'B'C'D'的位似中心,点B、C的坐标分别为(-8,2),(-4,0),点B'是点B的对应点,且点B'的横坐标为-1,则四边形A'B'C'D'的周长为__________.
13.如图所示,已知O是坐标原点,B,C两点的坐标分别为(3,-1),(2,1).
(1)以O点为位似中心在y轴左侧将△OBC各边放大为原来的两倍(即新图形与原图形的相似比为2),画出图形;
(2)如果△OBC内部一点M的坐标为(x,y),写出B、C、M对应点B',C',M'的坐标.
14.在平面直角坐标系中,已知点E(-4,2),F(-2,-2),以原点O为位似中心,
相似比为,把△EFO各边缩小,则点E的对应点E'的坐标是( )
A.(-2,1) B.(-8,4) C.(-8,4)或(8,-4) D.(-2,1)或(2,-1)
15.如图所示,已知△ABC与△DEF位似,位似中心为点O,且△ABC的面积等于△DEF面积的,则AO:AD=( )
A.2:3 B.2:5 C.4:9 D.4:13
16.如图所示,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=__________.
17.如图所示,以点O为位似中心,将五边形 ABCDE各边放大后得到五边形A'B'C'D'E',已知OA=10cm,OA'=20cm,则五边形 ABCDE的周长与五边形A'B'C'D'E'的周长的比是__________.
18.如图所示,△ABC中,A,B两个顶点在x轴的上方,点C的坐标是(-1,0)以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C,并把△ABC各边放大到原来的2倍设点B的对应点B'的横坐标是a,则点B的横坐标是__________.
19.如图所示,网格纸中的每个小方格都是边长为1的正方形,我们把以格点间连线为边的三角形称为“格点三角形”,图中的△ABC是格点三角形在建立平面直角坐标系后,点B的坐标为(-1,-1).
(1)把△ABC向下平移5格后得到△A1B1C1,写出点A1,B1,C1的坐标,并画出△A1B1C1;
(2)把△ABC绕点O按顺时针方向旋转180°后得到△A2B2C2,写出点A2,B2,C2的坐标,并画出△A2B2C2;
(3)把△ABC各边以点O为位似中心放大得到△A3B3C3,使放大前后对应线段的比为1:2,写出点A3,B3,C3的坐标,并画出△A3B3C3.
20.在如图所示的网格中,以点O为位似中心,四边形ABCD的位似图形是( )
A.四边形NPMQ B.四边形NPMR C.四边形NHMQ D.四边形NHMR
21.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,2),B(1,1),C(3,1),以原点O为位似中心,在原点的同侧画△DEF,使△DEF与△ABC成位似图形,且相似比为2:1,则线段DF的长度为( )
A. B.2 C.4 D.2
22.在平面直角坐标系中,△ABC和△A1B1C1的相似比等于,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是___________.
23.如图所示,在直角坐标系中,每个小正方形的边长均为1个单位长度,△ABO的顶点坐标分别为A(-2,-1),B(-2,-3),O(0,0),△A1B1O1的顶点坐标分别为A1(1,-1),B1(1,-5),O1(5,1),△ABO与△A1B1O1是以点P为位似中心的位似图形,则P点的坐标为___________.
24.如图所示,△ABC中,三个顶点的坐标分别是A(-2,2),B(-4,1),C(-1,-1).以点C为位似中心,在x轴下方作△ABC的位似图形△A′B′C′,并把△ABC的边长放大为原来的2倍,那么点A的坐标为( )
A.(3,-7) B.(1,-7) C.(4,-4) D.(1,-4)
参考答案
1.B
2.解析 是位似图形.
如图,(1)对应点的连线交于同一点;
设每个小正方形的边长为1,则DF=,AC=2,DE=2,AB=4,EF=,BC=2,三边对应成比例,两个三角形相似。
综合(1)(2)知,它们是位似图形,位似中心为P.
3.A 4.C 5.C 6. (-3,0)或(,)
7.解析 画出两组对应点的连线,找出它们的交点,即是位似中心,如图,P,O即为所求的位似中心.
8.解析 (1)如图,△A1B1C1即为所作.
(2)如图,△A2B2C2即为所作.
9.D 10.(-4,3)或(4,-3) 11.(2,)或(-2,-) 12.
13.解析 (1)如图所示,△B'C'O即为所求.
(2)如图所示,∵B、C两点的坐标分别为3,-1),(2,1),新图形与原图形的相似比为2,∴B'(-6,2),C'(-4,-2).
∵△OBC内部一点M的坐标为(x,y),∴其对应点M的坐标为(-2x,-2y).
14.D 15.B 16. 4.5 17. 1:2 18.
19.解析(1)如图所示,△A1B1C1即为所求.
点A1,B1,C1的坐标分别为(3,-2),(-1,-6),(5,-6).
(2)如图所示,△A2B2C2即为所求.
点A2,B2,C2的坐标分别为(-3,-3),(1,1),(-5,1).
(3)如图所示,△A3B3C3和△A′3B′3C′3即为所求,
点A3,B3,C3的坐标分别为(6,6),(-2,-2),(10,-2)或(-6,-6),(2,2),(-10,2).
20.A 21.D 22.(4,8)或(-4,-8) 23.(-5,-1) 24.B
_21?????????è?????(www.21cnjy.com)_
