6.4.3 余弦定理、正弦定理的综合应用-【新教材】人教A版(2019)高中数学必修第二册同步练习(word含解析)
文档属性
| 名称 | 6.4.3 余弦定理、正弦定理的综合应用-【新教材】人教A版(2019)高中数学必修第二册同步练习(word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 183.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 12:08:54 | ||
图片预览




文档简介
2020-2021学年高一数学人教A版(2019)必修第二册
6.4.3 余弦定理、正弦定理的综合应用 同步练习
学校:___________姓名:___________班级:___________学号:___________
一.选择题
在?ABC中,内角A,B,C的对边分别为a,b,c,已知(sinB?sinC)2=sin2A?sinBsinC,a=23,b=2,则?ABC的面积为(????)
A. 2 B. 23 C. 4 D. 43
有一长为10?m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长的长度(单位:m)是(????)
A. 5 B. 10 C. 102 D. 103
某人在C点测得某塔在南偏西80°方向上,塔顶A的仰角为45°,此人沿南偏东40°方向前进10?m到D,测得塔顶A的仰角为30°,则塔高为(????)
A. 15?m B. 5?m C. 10?m D. 12?m
如图所示,隔河可以看到对岸两目标A,B,但不能到达,现在岸边取相距4?km的C,D两点,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),则两目标A,B间的距离为(????)
A. 853?km B. 4153km C. 2153km D. 25km
已知锐角三角形ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos?2A=0,a=7,c=6,则b等于? (??? )
A. 10 B. 9 C. 8 D. 5
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20000m,速度为900km/?,飞行员先看到山顶的俯角为30?,经过80s后又看到山顶的俯角为75?,则山顶的海拔高度为(????)
A. 5000(3+1)m B. 5000(3?1)m C. 5000(3?3)m D. 5000(5?3)m
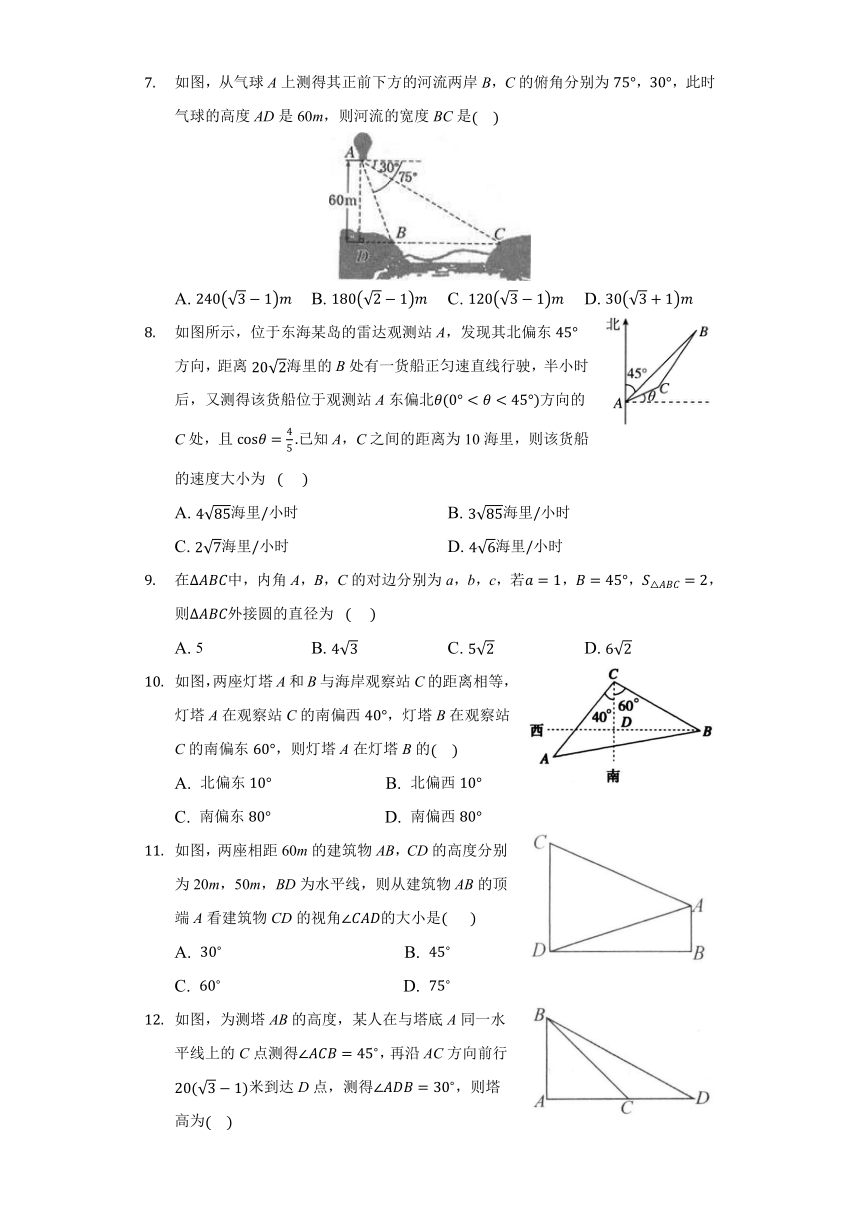
如图,从气球A上测得其正前下方的河流两岸B,C的俯角分别为75°,30°,此时气球的高度AD是60m,则河流的宽度BC是(????)
A. 2403?1m B. 1802?1m C. 1203?1m D. 303+1m
如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°方向,距离202海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北θ(0°<θ<45°)方向的C处,且cosθ=45.已知A,C之间的距离为10海里,则该货船的速度大小为? (??? )
A. 485海里/小时 B. 385海里/小时
C. 27海里/小时 D. 46海里/小时
在?ABC中,内角A,B,C的对边分别为a,b,c,若a=1,B=45°,S△ABC=2,则?ABC外接圆的直径为? (??? )
A. 5 B. 43 C. 52 D. 62
如图,两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站C的南偏西40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的(????)
A. 北偏东10° B. 北偏西10°
C. 南偏东80° D. 南偏西80°
如图,两座相距60m的建筑物AB,CD的高度分别为20m,50m,BD为水平线,则从建筑物AB的顶端A看建筑物CD的视角∠CAD的大小是(? ? )
A. 30? B. 45?
C. 60? D. 75?
如图,为测塔AB的高度,某人在与塔底A同一水平线上的C点测得∠ACB=45?,再沿AC方向前行20(3?1)米到达D点,测得∠ADB=30?,则塔高为(????)
403米 B. 203米 C. 40米 D. 20米
二.填空题
在?ABC中,已知a=32,cosC=13,S△ABC=43,则b=______.
如图,为测量塔的高度,在塔底所在的水平面内取一点C,测得塔顶的仰角为θ,由C向塔前进30米后到达点D,测得塔顶的仰角为2θ,再由D向塔前进103米后到达点E,测得塔顶的仰角为4θ,则塔高为_________米.
在?ABC中,内角A,B,C的对边分别为a,b,c,已知b2=ac且cosB=34.
(1)则1tanA+1tanC的值为_________;
(2)设BA?BC=32,则a+c的值为_________.
台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东方向40千米处,则B城市处于危险区内的时间为_______小时.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,∠MAC=75°,从C点测得∠MCA=60°.已知山高BC=100?m,则MN=_______m.
在?ABC中,内角A,B,C所对的边分别为a,b,c,已知?ABC的面积为315,b?c=2,cosA=?14,则a的值为__________.
三.解答题
在?ABC中,a,b,c分别为角A,B,C所对的边,角C是钝角,且sinB=b2c.
(Ⅰ)求角C的值;
(Ⅱ)若b=2,?ABC的面积为3,求c的值.
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡角为15°的观礼台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部B的仰角分别为60°和30°,第一排和最后一排的距离为106米(如图所示),旗杆底部与第一排在同一水平面上,若国歌播放的时间约为50秒,升旗手应以约多大的速度匀速升旗?
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N?(异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
答案和解析
一.选择题
1.【答案】B
【解析】解:∵(sinB?sinC)2=sin2A?sinBsinC,
∴sin2B+sin2C?2sinBsinC=sin2A?sinBsinC,
∴由正弦定理可得b2+c2?2bc=a2?bc,可得b2+c2?a2=bc,
∴由余弦定理可得cosA=b2+c2?a22bc=bc2bc=12,由A∈(0,π),可得A=π3,
∵sinA=32,
∵a=23,b=2,
∴由正弦定理可得sinB=b?sinAa=2×3223=12,由b∴C=π?A?B=π2,
∴△ABC的面积S=12ab=12×23×2=23.
故选:B.
由已知利用平方差公式,正弦定理,余弦定理可求cosA=12,由A∈(0,π),可得A=π3,由正弦定理可得sinB=12,由b本题主要考查了平方差公式,正弦定理,余弦定理,三角形内角和定理,三角形的面积公式在解三角形中的应用,考查了转化思想,属于基础题.
2.【答案】C
【解析】
【分析】
本题的考点是解三角形的实际应用,主要考查正弦定理的应用,考查三角形模型的构建,属于中档题.
由题意画出图形,利用正弦定理求出坡底要延长的距离AB即可.
【解答】
解:由题意可知PA=10,∠PAO=75°,
∠B=30°,∠BPA=45°,
如图:∠PAB=180°?75°=105°,
由正弦定理ABsin45°=PAsin30°,
可得AB=10×sin45°12=102.
即坡底要延长102m.
故选C.
3.【答案】C
【解析】
【分析】本题考查解三角形的实际应用以及余弦定理的应用,属于中档题.
作出图形,设塔高为??m.在Rt△AOC中,∠ACO=45°,则OC=OA=?.
在Rt?AOD中,∠ADO=30°,则OD=3?.在△OCD中,运用余弦定理,建立h的方程,解得h的值,即可得到答案.
【解答】
解:如图所示,设塔高为??m.
在Rt?AOC中,∠ACO=45°,则OC=OA=?.
在Rt?AOD中,∠ADO=30°,则OD=3?.
在?OCD中,∠OCD=120°,CD=10.
由余弦定理,得OD2=OC2+CD2?2OC·CDcos∠OCD,
即,
所以h2?5??50=0,
解得?=10或?=?5(舍).
故选C.
4.【答案】B
【解析】
【分析】
本题主要考查了正弦定理、余弦定理在解三角形中的应用问题,也考查了计算求解能力和转化思想,是中档题.
在?ACD中由正弦定理可求AD的值,在?BCD中由正弦定理可求BD的值,再在?ABD中由余弦定理可求AB的值.
【解答】
解:由已知,?ACD中,∠ADC=30°,∠ACD=120°,可得∠CAD=30°,
由正弦定理,得,
所以;
?BCD中,∠CDB=75°,∠BCD=45°,可得∠CBD=60°,
由正弦定理,得,
所以;
?ABD中,由余弦定理,得
AB2=AD2+BD2?2AD?BD?cos∠ADB=48+323?2×43×463×22=803,
解得:AB=4153,
则两目标A,B间的距离为4153km.
故选:B.
5.【答案】D
【解析】
【分析】
本题考查余弦定理,二倍角的余弦函数公式,熟练掌握余弦定理是解本题的关键.
利用二倍角的余弦函数公式化简已知的等式,求出cosA的值,再由a与c的值,利用余弦定理即可求出b的值.
【解答】
解:∵23cos2A+cos2A=23cos2A+2cos2A?1=0,
∴cos2A=125,A为锐角,
∴cosA=15,
又∵a=7,c=6,
根据余弦定理得:a2=b2+c2?2bc?cosA,
∴49=b2+36?125b,
∴解得:b=5或b=?135(舍去),
∴b=5.
故选D.
6.【答案】C
【解析】
【分析】本题考查了正弦定理与直角三角形的边角关系应用问题,属于中档题.
根据题意画出图形,结合图形利用正弦定理和直角三角形的边角关系,即可求出山顶的海拔高度.
【解答】
解:如图,过点C作CD⊥AB于点D.
由题意知∠A=30?,∠CBD=75?,
则∠ACB=45?,AB=900×80×13600=20(km).
∴在?ABC中,由正弦定理,得BC=102(km).
∵CD⊥AD,
∴CD=BCsin∠CBD=BC×sin75?=102sin75?=5+53(km).
山顶的海拔高度为[20?(5+53)]km=5000(3?3)m.
故选C.
7.【答案】C
【解析】
【分析】
本题给出实际应用问题,求河流在B、C两地的宽度,着重考查了三角函数的定义、正余弦定理解三角形的知识,属于中档题.
【解答】
解:如图,∠DAB=15°,
∵tan15°=tan(45°?30°)=2?3.
在Rt?ADB中,又AD=60,∴DB=AD?tan15°=120?603.
在Rt?ADC中,∠DAC=60°,AD=60,∴DC=AD?tan60°=603.
∴BC=DC?DB=603?(120?603)=120(3?1)(m),
∴河流的宽度BC等于120(3?1)m.
故选C.
8.【答案】A
【解析】
【分析】
本题主要考查解三角形的应用,余弦定理的应用,属于中档题.
根据条件求出cos∠BAC,以及利用余弦定理求出BC的长度是解决本题的关键.
【解答】
解:∵cosθ=45,
∴sinθ=35,由题意得∠BAC=45°?θ,
即cos∠BAC=cos(45°?θ)=22×(45+35)=7210,
∵AB=202,AC=10,
∴由余弦定理得BC2=AB2+AC2?2AB?ACcos∠BAC,
即BC2=(202)2+102?2×202×10×7210=800+100?560=340,
即BC=340=285,
设船速为x,
则12x=285,
∴x=485(海里/小时),
故选A.
9.【答案】C
【解析】
【分析】本题考查正余弦定理的应用,三角形面积公式,考查运算化简的能力,属于基础题,先由三角形面积公式求得c=42,由余弦定理求得b=5,利用正弦定理可得.
【解答】
解:∵S△ABC=2,
.
∴12×1×c×22=2,
∴c=42.
false
∴b2=12+(42)2?2×1×42×22=25,
∴b=5.
设△ABC的外接圆半径为R.
,
.
故选C.
10.【答案】D
【解析】
【分析】本题考查解三角形的实际应用,解答此类题需要正确画出方位角.
根据图正确表示出方位角,即可求解.
【解答】解:由条件及题图可知,∠A=∠B=40°,
又∠BCD=60°,所以∠CBD=30°,所以∠DBA=10°,
因此灯塔A在灯塔B南偏西80°.
11.【答案】B
【解析】
【分析】本题为解三角形的题目,考查利用余弦定理解三角形,题目基础.
首先分别求得AD2=4000,AC2=4500,进而利用余弦定理求得cos∠CAD的值,即可求解.
【解答】
解:AD2=602+202=4000,
AC2=602+302=4500.
在△CAD中,由余弦定理,得cos∠CAD=AD2+AC2?CD22AD?AC=22,
故∠CAD=45?.
故选B.
12.【答案】D
【解析】
【分析】本题为解三角形实际应用问题,题目基础.
首先设出关键量AB=x,在直角三角形中利用30°角的正切值求解即可.
【解答】
解:Rt?ABC中,设AB=x,
则由∠ACB=45?可知AC=x,
在Rt?ABD中,AD=x+20(3?1),∠ADB=30?,
∴xx+20(3?1)=tan30?,即x+20(3?1)x=3,
解得x=20.
则塔高为20米.
故选D.
13.【答案】23
【解析】
【分析】
此题考查了三角形面积公式,以及同角三角函数的基本关系,熟练掌握公式是解本题的关键,属于基础题.
由cosC的值,利用同角三角函数的基本关系求出sinC的值,利用三角形面积公式列出关系式,把a,sinC以及已知面积代入求出b的值即可.
【解答】
解:∵?ABC中,cosC=13,
∴sinC=1?cos2C=223,
∵a=32,S△ABC=43,
∴12absinC=43,
即12×32b×223=43,
解得:b=23,
故答案为:23.
14.【答案】15
【解析】
【分析】
本题考查余弦定理、解三角形的实际应用,属于中档题.
根据题意求出PE=DE=103,在三角形PDE中,由余弦定理得cos2θ=PD2+DE2?PE22PD·DE,求出,利用sin4θ=PAPE,即可求出结果.
【解答】
解:∵∠CPD=∠EDP?∠DCP=2θ?θ=θ,??
∴PD=CD=30,∠DPE=∠AEP?∠EDP=4θ?2θ=2θ,????
∴PE=DE=103,
在三角形PDE中,由余弦定理得
cos2θ=PD2+DE2?PE22PD·DE=302+1032?10322×30×103=32,
由图可以2θ为锐角,
,
,
∴sin4θ=PAPE=32,
∴PA=PE·sin4θ=103×32=15.
故答案为15.
15.【答案】(1)477? ;(2)3
【解析】
【分析】
本题考查正弦定理,余弦定理的应用,属于基础题.
先求sinB=1?342=74,再有正弦定理得sin2B=sin?A sin?C,切化弦得1tan?A+1tan?C=cos?Asin?A+cos?Csin?C=1sinB,;
由BA?BC=32,得accosB=32,再利用余弦定理得(a+c)2=9,解得.
【解答】
解:(1)由cosB=34,B∈(0,π),得sinB=1?342=74.?
由b2=ac及正弦定理,得sin2B=sin?A sin?C.?
于是1tanA+1tanC=cosAsinA+cosCsinC=sinCcosA+cosCsinAsinAsinC=
sin(A+C)sin2B=sinBsin2B=1sinB=477.
由BA?BC=32,有accosB=32,
∴ac=2,
又由b2=ac及余弦定理,得a2+c2?b2=2accos?B,?
即a2+c2?2=3,a2+2ac+c2=2ac+5,
得(a+c)2=9,
∴a+c=3.
16.【答案】1
【解析】
【分析】
本题考查余弦定理在解三角形中的应用,属于基础题.
设A地东北方向上存在点P到B的距离为30千米,设AP=x千米,根据余弦定理得出PB2=AP2+AB2?2AP·AB·cos?A,即x2?402x+700=0,结合根与系数的关系求出|x1?x2|,即可求出结果.
【解答】
解:设A地东北方向上存在点P到B的距离为30千米,设AP=x千米,
在?ABP中,PB2=AP2+AB2?2AP·AB·cos?A,
即302=x2+402?2x·40cos?45°,得x2?402x+700=0,
设方程x2?402x+700=0的两根为x1,x2,
则x1+x2=402,x1x2=700,
故|x1?x2|2=(x1+x2)2?4x1x2=400,即|x1?x2|=20,
故B城市处于危险区内的时间为2020=1(小时).
故答案为1.
17.【答案】150
【解析】
【分析】
本题考查了解三角形的实际应用,考查了正弦定理,属于中档题.
在三角形ABC中,由正弦定理得MAsin60°=ACsin45°,解得MA=1003?m,在三角形MNA中,MN1003=sin60°=32,可得山高MN的值.
【解答】
解:在三角形ABC中,AC=1002?m,
在三角形MAC中,MAsin60°=ACsin45°,解得MA=1003?m,
在三角形MNA中,MN1003=sin60°=32,
故MN=150?m,即山高MN为150?m.
故答案为150.
18.【答案】8
【解析】
【分析】
本题主要考查利用余弦定理解三角形,首先通过sin2A+cos2A=1,以及sinA为正数求出sinA,再结合S△ABC=315,和b?c=2,求出b、c的值,从而解得答案,难度较易,属于基础题.
【解答】
解:因为?ABC的面积为315,即,
由题意知b?c=2,
又sin2A+cos2A=1.
故,
联立解得b=6,c=4(负数舍去),
由余弦定理,得,
解得a=8(负数舍去).
故答案为8.
19.【答案】解:(Ⅰ)由sinB=b2c得2csinB=b,由正弦定理得:2sinCsinB=sinB,
所以sinB(2sinC?1)=0,…(3分)
因为sinB≠0,
所以sinC=12,
因为C是钝角,
所以C=5π6.??…(6分)
(Ⅱ)因为S=12absinC=12a=3,a=23,…(9分)
由余弦定理得c2=a2+b2?2abcosC=12+4?2×23×2×(?32)=28,
所以c=27,即c的值为27.???????…(12分)
【解析】(Ⅰ)由正弦定理化简已知可得sinB(2sinC?1)=0,由sinB≠0解得sinC=12,结合C是钝角,即可解得C的值.
(Ⅱ)由已知及三角形面积公式可求a的值,由余弦定理即可解得c的值.
本题主要考查了正弦定理,余弦定理,三角形面积公式,正弦函数的图象和性质在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.
20.【答案】解:在?BCD中,∠BDC=30°+15°=45°,
∠CBD=180°?45°?105°=30°,CD=106,
由正弦定理,得BC=CDsin45°sin30°=203;
在Rt?ABC中,AB=BCsin?60°=203×32=30(米).
所以升旗速度v=ABt=3050=0.6(米/秒).
【解析】本题考查解三角形的实际应用及正弦定理,属于基础题.
根据题意可求得,∠BDC=45°,∠CBD=30°,CD=106,然后利用正弦定理求得BC,最后在Rt?ABC中利用AB=BCsin?60°求得答案.
21.【答案】解:设∠AMN=θ,在?AMN中,MNsin60?=AMsin(120??θ).
因为MN=2,所以AM=433sin(120°?θ).? ? ? ? ? ? ? ?
在?APM中,cos∠AMP=cos(60°+θ).? ? ? ? ? ? ? ? ?
AP2=AM2+MP2?2AM?MP?cos∠AMP
=163sin2(120°?θ)+4?2×2×433?sin(120°?θ)?cos(60°+θ)? ? ? ? ?
=163sin2(θ+60°)?1633?sin(θ+60°)?cos(θ+60°)+4
=83[1?cos?(2θ+120°)]?833?sin(2θ+120°)+4
=?83[3sin(2θ+120°)+cos?(2θ+120°)]+203
=203?163sin(2θ+150°),θ∈(0,120°).? ? ? ? ? ? ? ? ?
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值23.
答:设计∠AMN为60°时,工厂产生的噪声对居民的影响最小.
【解析】设∠AMN=θ,在△AMN中,求出AM,在?APM中,利用余弦定理,建立函数,利用辅助角公式化简,即可得出结论.
本题考查正弦定理、余弦定理的运用,考查三角函数的化简,正确构建函数是关键.
6.4.3 余弦定理、正弦定理的综合应用 同步练习
学校:___________姓名:___________班级:___________学号:___________
一.选择题
在?ABC中,内角A,B,C的对边分别为a,b,c,已知(sinB?sinC)2=sin2A?sinBsinC,a=23,b=2,则?ABC的面积为(????)
A. 2 B. 23 C. 4 D. 43
有一长为10?m的斜坡,倾斜角为75°,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30°,则坡底要延长的长度(单位:m)是(????)
A. 5 B. 10 C. 102 D. 103
某人在C点测得某塔在南偏西80°方向上,塔顶A的仰角为45°,此人沿南偏东40°方向前进10?m到D,测得塔顶A的仰角为30°,则塔高为(????)
A. 15?m B. 5?m C. 10?m D. 12?m
如图所示,隔河可以看到对岸两目标A,B,但不能到达,现在岸边取相距4?km的C,D两点,测得∠ACB=75°,∠BCD=45°,∠ADC=30°,∠ADB=45°(A,B,C,D在同一平面内),则两目标A,B间的距离为(????)
A. 853?km B. 4153km C. 2153km D. 25km
已知锐角三角形ABC的内角A,B,C的对边分别为a,b,c,23cos2A+cos?2A=0,a=7,c=6,则b等于? (??? )
A. 10 B. 9 C. 8 D. 5
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔20000m,速度为900km/?,飞行员先看到山顶的俯角为30?,经过80s后又看到山顶的俯角为75?,则山顶的海拔高度为(????)
A. 5000(3+1)m B. 5000(3?1)m C. 5000(3?3)m D. 5000(5?3)m
如图,从气球A上测得其正前下方的河流两岸B,C的俯角分别为75°,30°,此时气球的高度AD是60m,则河流的宽度BC是(????)
A. 2403?1m B. 1802?1m C. 1203?1m D. 303+1m
如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°方向,距离202海里的B处有一货船正匀速直线行驶,半小时后,又测得该货船位于观测站A东偏北θ(0°<θ<45°)方向的C处,且cosθ=45.已知A,C之间的距离为10海里,则该货船的速度大小为? (??? )
A. 485海里/小时 B. 385海里/小时
C. 27海里/小时 D. 46海里/小时
在?ABC中,内角A,B,C的对边分别为a,b,c,若a=1,B=45°,S△ABC=2,则?ABC外接圆的直径为? (??? )
A. 5 B. 43 C. 52 D. 62
如图,两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站C的南偏西40°,灯塔B在观察站C的南偏东60°,则灯塔A在灯塔B的(????)
A. 北偏东10° B. 北偏西10°
C. 南偏东80° D. 南偏西80°
如图,两座相距60m的建筑物AB,CD的高度分别为20m,50m,BD为水平线,则从建筑物AB的顶端A看建筑物CD的视角∠CAD的大小是(? ? )
A. 30? B. 45?
C. 60? D. 75?
如图,为测塔AB的高度,某人在与塔底A同一水平线上的C点测得∠ACB=45?,再沿AC方向前行20(3?1)米到达D点,测得∠ADB=30?,则塔高为(????)
403米 B. 203米 C. 40米 D. 20米
二.填空题
在?ABC中,已知a=32,cosC=13,S△ABC=43,则b=______.
如图,为测量塔的高度,在塔底所在的水平面内取一点C,测得塔顶的仰角为θ,由C向塔前进30米后到达点D,测得塔顶的仰角为2θ,再由D向塔前进103米后到达点E,测得塔顶的仰角为4θ,则塔高为_________米.
在?ABC中,内角A,B,C的对边分别为a,b,c,已知b2=ac且cosB=34.
(1)则1tanA+1tanC的值为_________;
(2)设BA?BC=32,则a+c的值为_________.
台风中心从A地以每小时20千米的速度向东北方向移动,离台风中心30千米内的地区为危险区,城市B在A的正东方向40千米处,则B城市处于危险区内的时间为_______小时.
如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点,从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°,∠MAC=75°,从C点测得∠MCA=60°.已知山高BC=100?m,则MN=_______m.
在?ABC中,内角A,B,C所对的边分别为a,b,c,已知?ABC的面积为315,b?c=2,cosA=?14,则a的值为__________.
三.解答题
在?ABC中,a,b,c分别为角A,B,C所对的边,角C是钝角,且sinB=b2c.
(Ⅰ)求角C的值;
(Ⅱ)若b=2,?ABC的面积为3,求c的值.
某校运动会开幕式上举行升旗仪式,旗杆正好处在坡角为15°的观礼台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部B的仰角分别为60°和30°,第一排和最后一排的距离为106米(如图所示),旗杆底部与第一排在同一水平面上,若国歌播放的时间约为50秒,升旗手应以约多大的速度匀速升旗?
如图,经过村庄A有两条夹角为60°的公路AB,AC,根据规划拟在两条公路之间的区域内建一工厂P,分别在两条公路边上建两个仓库M、N?(异于村庄A),要求PM=PN=MN=2(单位:千米).如何设计,使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远).
答案和解析
一.选择题
1.【答案】B
【解析】解:∵(sinB?sinC)2=sin2A?sinBsinC,
∴sin2B+sin2C?2sinBsinC=sin2A?sinBsinC,
∴由正弦定理可得b2+c2?2bc=a2?bc,可得b2+c2?a2=bc,
∴由余弦定理可得cosA=b2+c2?a22bc=bc2bc=12,由A∈(0,π),可得A=π3,
∵sinA=32,
∵a=23,b=2,
∴由正弦定理可得sinB=b?sinAa=2×3223=12,由b
∴△ABC的面积S=12ab=12×23×2=23.
故选:B.
由已知利用平方差公式,正弦定理,余弦定理可求cosA=12,由A∈(0,π),可得A=π3,由正弦定理可得sinB=12,由b
2.【答案】C
【解析】
【分析】
本题的考点是解三角形的实际应用,主要考查正弦定理的应用,考查三角形模型的构建,属于中档题.
由题意画出图形,利用正弦定理求出坡底要延长的距离AB即可.
【解答】
解:由题意可知PA=10,∠PAO=75°,
∠B=30°,∠BPA=45°,
如图:∠PAB=180°?75°=105°,
由正弦定理ABsin45°=PAsin30°,
可得AB=10×sin45°12=102.
即坡底要延长102m.
故选C.
3.【答案】C
【解析】
【分析】本题考查解三角形的实际应用以及余弦定理的应用,属于中档题.
作出图形,设塔高为??m.在Rt△AOC中,∠ACO=45°,则OC=OA=?.
在Rt?AOD中,∠ADO=30°,则OD=3?.在△OCD中,运用余弦定理,建立h的方程,解得h的值,即可得到答案.
【解答】
解:如图所示,设塔高为??m.
在Rt?AOC中,∠ACO=45°,则OC=OA=?.
在Rt?AOD中,∠ADO=30°,则OD=3?.
在?OCD中,∠OCD=120°,CD=10.
由余弦定理,得OD2=OC2+CD2?2OC·CDcos∠OCD,
即,
所以h2?5??50=0,
解得?=10或?=?5(舍).
故选C.
4.【答案】B
【解析】
【分析】
本题主要考查了正弦定理、余弦定理在解三角形中的应用问题,也考查了计算求解能力和转化思想,是中档题.
在?ACD中由正弦定理可求AD的值,在?BCD中由正弦定理可求BD的值,再在?ABD中由余弦定理可求AB的值.
【解答】
解:由已知,?ACD中,∠ADC=30°,∠ACD=120°,可得∠CAD=30°,
由正弦定理,得,
所以;
?BCD中,∠CDB=75°,∠BCD=45°,可得∠CBD=60°,
由正弦定理,得,
所以;
?ABD中,由余弦定理,得
AB2=AD2+BD2?2AD?BD?cos∠ADB=48+323?2×43×463×22=803,
解得:AB=4153,
则两目标A,B间的距离为4153km.
故选:B.
5.【答案】D
【解析】
【分析】
本题考查余弦定理,二倍角的余弦函数公式,熟练掌握余弦定理是解本题的关键.
利用二倍角的余弦函数公式化简已知的等式,求出cosA的值,再由a与c的值,利用余弦定理即可求出b的值.
【解答】
解:∵23cos2A+cos2A=23cos2A+2cos2A?1=0,
∴cos2A=125,A为锐角,
∴cosA=15,
又∵a=7,c=6,
根据余弦定理得:a2=b2+c2?2bc?cosA,
∴49=b2+36?125b,
∴解得:b=5或b=?135(舍去),
∴b=5.
故选D.
6.【答案】C
【解析】
【分析】本题考查了正弦定理与直角三角形的边角关系应用问题,属于中档题.
根据题意画出图形,结合图形利用正弦定理和直角三角形的边角关系,即可求出山顶的海拔高度.
【解答】
解:如图,过点C作CD⊥AB于点D.
由题意知∠A=30?,∠CBD=75?,
则∠ACB=45?,AB=900×80×13600=20(km).
∴在?ABC中,由正弦定理,得BC=102(km).
∵CD⊥AD,
∴CD=BCsin∠CBD=BC×sin75?=102sin75?=5+53(km).
山顶的海拔高度为[20?(5+53)]km=5000(3?3)m.
故选C.
7.【答案】C
【解析】
【分析】
本题给出实际应用问题,求河流在B、C两地的宽度,着重考查了三角函数的定义、正余弦定理解三角形的知识,属于中档题.
【解答】
解:如图,∠DAB=15°,
∵tan15°=tan(45°?30°)=2?3.
在Rt?ADB中,又AD=60,∴DB=AD?tan15°=120?603.
在Rt?ADC中,∠DAC=60°,AD=60,∴DC=AD?tan60°=603.
∴BC=DC?DB=603?(120?603)=120(3?1)(m),
∴河流的宽度BC等于120(3?1)m.
故选C.
8.【答案】A
【解析】
【分析】
本题主要考查解三角形的应用,余弦定理的应用,属于中档题.
根据条件求出cos∠BAC,以及利用余弦定理求出BC的长度是解决本题的关键.
【解答】
解:∵cosθ=45,
∴sinθ=35,由题意得∠BAC=45°?θ,
即cos∠BAC=cos(45°?θ)=22×(45+35)=7210,
∵AB=202,AC=10,
∴由余弦定理得BC2=AB2+AC2?2AB?ACcos∠BAC,
即BC2=(202)2+102?2×202×10×7210=800+100?560=340,
即BC=340=285,
设船速为x,
则12x=285,
∴x=485(海里/小时),
故选A.
9.【答案】C
【解析】
【分析】本题考查正余弦定理的应用,三角形面积公式,考查运算化简的能力,属于基础题,先由三角形面积公式求得c=42,由余弦定理求得b=5,利用正弦定理可得.
【解答】
解:∵S△ABC=2,
.
∴12×1×c×22=2,
∴c=42.
false
∴b2=12+(42)2?2×1×42×22=25,
∴b=5.
设△ABC的外接圆半径为R.
,
.
故选C.
10.【答案】D
【解析】
【分析】本题考查解三角形的实际应用,解答此类题需要正确画出方位角.
根据图正确表示出方位角,即可求解.
【解答】解:由条件及题图可知,∠A=∠B=40°,
又∠BCD=60°,所以∠CBD=30°,所以∠DBA=10°,
因此灯塔A在灯塔B南偏西80°.
11.【答案】B
【解析】
【分析】本题为解三角形的题目,考查利用余弦定理解三角形,题目基础.
首先分别求得AD2=4000,AC2=4500,进而利用余弦定理求得cos∠CAD的值,即可求解.
【解答】
解:AD2=602+202=4000,
AC2=602+302=4500.
在△CAD中,由余弦定理,得cos∠CAD=AD2+AC2?CD22AD?AC=22,
故∠CAD=45?.
故选B.
12.【答案】D
【解析】
【分析】本题为解三角形实际应用问题,题目基础.
首先设出关键量AB=x,在直角三角形中利用30°角的正切值求解即可.
【解答】
解:Rt?ABC中,设AB=x,
则由∠ACB=45?可知AC=x,
在Rt?ABD中,AD=x+20(3?1),∠ADB=30?,
∴xx+20(3?1)=tan30?,即x+20(3?1)x=3,
解得x=20.
则塔高为20米.
故选D.
13.【答案】23
【解析】
【分析】
此题考查了三角形面积公式,以及同角三角函数的基本关系,熟练掌握公式是解本题的关键,属于基础题.
由cosC的值,利用同角三角函数的基本关系求出sinC的值,利用三角形面积公式列出关系式,把a,sinC以及已知面积代入求出b的值即可.
【解答】
解:∵?ABC中,cosC=13,
∴sinC=1?cos2C=223,
∵a=32,S△ABC=43,
∴12absinC=43,
即12×32b×223=43,
解得:b=23,
故答案为:23.
14.【答案】15
【解析】
【分析】
本题考查余弦定理、解三角形的实际应用,属于中档题.
根据题意求出PE=DE=103,在三角形PDE中,由余弦定理得cos2θ=PD2+DE2?PE22PD·DE,求出,利用sin4θ=PAPE,即可求出结果.
【解答】
解:∵∠CPD=∠EDP?∠DCP=2θ?θ=θ,??
∴PD=CD=30,∠DPE=∠AEP?∠EDP=4θ?2θ=2θ,????
∴PE=DE=103,
在三角形PDE中,由余弦定理得
cos2θ=PD2+DE2?PE22PD·DE=302+1032?10322×30×103=32,
由图可以2θ为锐角,
,
,
∴sin4θ=PAPE=32,
∴PA=PE·sin4θ=103×32=15.
故答案为15.
15.【答案】(1)477? ;(2)3
【解析】
【分析】
本题考查正弦定理,余弦定理的应用,属于基础题.
先求sinB=1?342=74,再有正弦定理得sin2B=sin?A sin?C,切化弦得1tan?A+1tan?C=cos?Asin?A+cos?Csin?C=1sinB,;
由BA?BC=32,得accosB=32,再利用余弦定理得(a+c)2=9,解得.
【解答】
解:(1)由cosB=34,B∈(0,π),得sinB=1?342=74.?
由b2=ac及正弦定理,得sin2B=sin?A sin?C.?
于是1tanA+1tanC=cosAsinA+cosCsinC=sinCcosA+cosCsinAsinAsinC=
sin(A+C)sin2B=sinBsin2B=1sinB=477.
由BA?BC=32,有accosB=32,
∴ac=2,
又由b2=ac及余弦定理,得a2+c2?b2=2accos?B,?
即a2+c2?2=3,a2+2ac+c2=2ac+5,
得(a+c)2=9,
∴a+c=3.
16.【答案】1
【解析】
【分析】
本题考查余弦定理在解三角形中的应用,属于基础题.
设A地东北方向上存在点P到B的距离为30千米,设AP=x千米,根据余弦定理得出PB2=AP2+AB2?2AP·AB·cos?A,即x2?402x+700=0,结合根与系数的关系求出|x1?x2|,即可求出结果.
【解答】
解:设A地东北方向上存在点P到B的距离为30千米,设AP=x千米,
在?ABP中,PB2=AP2+AB2?2AP·AB·cos?A,
即302=x2+402?2x·40cos?45°,得x2?402x+700=0,
设方程x2?402x+700=0的两根为x1,x2,
则x1+x2=402,x1x2=700,
故|x1?x2|2=(x1+x2)2?4x1x2=400,即|x1?x2|=20,
故B城市处于危险区内的时间为2020=1(小时).
故答案为1.
17.【答案】150
【解析】
【分析】
本题考查了解三角形的实际应用,考查了正弦定理,属于中档题.
在三角形ABC中,由正弦定理得MAsin60°=ACsin45°,解得MA=1003?m,在三角形MNA中,MN1003=sin60°=32,可得山高MN的值.
【解答】
解:在三角形ABC中,AC=1002?m,
在三角形MAC中,MAsin60°=ACsin45°,解得MA=1003?m,
在三角形MNA中,MN1003=sin60°=32,
故MN=150?m,即山高MN为150?m.
故答案为150.
18.【答案】8
【解析】
【分析】
本题主要考查利用余弦定理解三角形,首先通过sin2A+cos2A=1,以及sinA为正数求出sinA,再结合S△ABC=315,和b?c=2,求出b、c的值,从而解得答案,难度较易,属于基础题.
【解答】
解:因为?ABC的面积为315,即,
由题意知b?c=2,
又sin2A+cos2A=1.
故,
联立解得b=6,c=4(负数舍去),
由余弦定理,得,
解得a=8(负数舍去).
故答案为8.
19.【答案】解:(Ⅰ)由sinB=b2c得2csinB=b,由正弦定理得:2sinCsinB=sinB,
所以sinB(2sinC?1)=0,…(3分)
因为sinB≠0,
所以sinC=12,
因为C是钝角,
所以C=5π6.??…(6分)
(Ⅱ)因为S=12absinC=12a=3,a=23,…(9分)
由余弦定理得c2=a2+b2?2abcosC=12+4?2×23×2×(?32)=28,
所以c=27,即c的值为27.???????…(12分)
【解析】(Ⅰ)由正弦定理化简已知可得sinB(2sinC?1)=0,由sinB≠0解得sinC=12,结合C是钝角,即可解得C的值.
(Ⅱ)由已知及三角形面积公式可求a的值,由余弦定理即可解得c的值.
本题主要考查了正弦定理,余弦定理,三角形面积公式,正弦函数的图象和性质在解三角形中的综合应用,考查了计算能力和转化思想,属于中档题.
20.【答案】解:在?BCD中,∠BDC=30°+15°=45°,
∠CBD=180°?45°?105°=30°,CD=106,
由正弦定理,得BC=CDsin45°sin30°=203;
在Rt?ABC中,AB=BCsin?60°=203×32=30(米).
所以升旗速度v=ABt=3050=0.6(米/秒).
【解析】本题考查解三角形的实际应用及正弦定理,属于基础题.
根据题意可求得,∠BDC=45°,∠CBD=30°,CD=106,然后利用正弦定理求得BC,最后在Rt?ABC中利用AB=BCsin?60°求得答案.
21.【答案】解:设∠AMN=θ,在?AMN中,MNsin60?=AMsin(120??θ).
因为MN=2,所以AM=433sin(120°?θ).? ? ? ? ? ? ? ?
在?APM中,cos∠AMP=cos(60°+θ).? ? ? ? ? ? ? ? ?
AP2=AM2+MP2?2AM?MP?cos∠AMP
=163sin2(120°?θ)+4?2×2×433?sin(120°?θ)?cos(60°+θ)? ? ? ? ?
=163sin2(θ+60°)?1633?sin(θ+60°)?cos(θ+60°)+4
=83[1?cos?(2θ+120°)]?833?sin(2θ+120°)+4
=?83[3sin(2θ+120°)+cos?(2θ+120°)]+203
=203?163sin(2θ+150°),θ∈(0,120°).? ? ? ? ? ? ? ? ?
当且仅当2θ+150°=270°,即θ=60°时,AP2取得最大值12,即AP取得最大值23.
答:设计∠AMN为60°时,工厂产生的噪声对居民的影响最小.
【解析】设∠AMN=θ,在△AMN中,求出AM,在?APM中,利用余弦定理,建立函数,利用辅助角公式化简,即可得出结论.
本题考查正弦定理、余弦定理的运用,考查三角函数的化简,正确构建函数是关键.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
