8.5.3.2平面与平面平行的性质 -【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步练习(Word含解析)
文档属性
| 名称 | 8.5.3.2平面与平面平行的性质 -【新教材】2020-2021学年人教A版(2019)高中数学必修第二册同步练习(Word含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 362.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 12:21:31 | ||
图片预览

文档简介
8.5.3 平面与平面平行第 2课时平面与平面平行的性质 -【新教材】人教A版(2019)高中数学必修第二册同步练习(含解析)
学校:___________姓名:___________班级:___________学号:___________
一.选择题
两个平行平面与另两个平行平面相交所得四条直线的位置关系是(????)
A. 两两互相平行 B. 两两相交于同一点
C. 两两相交但不一定交于同一点 D. 两两互相平行或交于同一点
平面α//平面β,点A,C∈α,B,D∈β,则直线AC//直线BD的充要条件是(????)
A. AB//CD B. AD//CB
C. AB与CD相交 D. A,B,C,D四点共面
若平面α?//平面β,平面γ?//平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是(????)
A. 互相平行 B. 交于一点 C. 互相异面 D. 不能确定
如图,在多面体ABCDEFG中,平面ABC?//平面DEFG,EF?//DG,AB=DE,DG=2EF,则(????)
A. BF//平面ACGD
B. CF//平面ABED
C. BC//FG
D. 平面ABED//平面CGF
如图,四棱锥P?ABCD的底面ABCD是平行四边形,M,N分别为棱PC,PB上的点,若PM∶MC=3∶1,且AN//平面BDM,则PN∶NB=?(????)?
A. 4∶1 B. 3∶1
C. 3∶2 D. 2∶1
已知四棱柱ABCD?A1B1C1D1的底面是平行四边形,过此四棱柱任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有? (??? )
A. 4条 B. 6条 C. 10条 D. 12条
α,β,γ为三个不重合的平面,a,b,c为三条不同的直线,则下列命题中不正确的是(????)
①a//cb//c?a//b;②a//γb//γ?a//b;③α//cβ//c?α//β;
④α//γβ//γ?α//β;⑤α//ca//c?α//a;⑥α//γa//γ?a//α.
A. ④⑥ B. ②③⑥ C. ②③⑤⑥ D. ②③
如图所示,P是三角形ABC所在平面外一点,平面α//平面ABC,α分别交线段PA,PB,PC于A′,B′,C′,若PA′:AA′=2:3,则S△A′B′C′:S△ABC=(????)
A. 2:25 B. 4:25
C. 2:5 D. 4:5
如图所示,四棱台ABCD?A′B′C′D′的底面为正方形,M为CC′的中点,点N在线段AB上,且AB=4BN.若MN?//平面ADD′A′,则此棱台上、下底面边长的比值为(????)
A. 15 B. 14
C. 13 D. 12
已知正方体ABCD?A1B1C1D1的棱长为2,点P在线段CB1上,且B1P=2PC,平面α经过点A,P,C1,则正方体ABCD?A1B1C1D1被平面α截得的截面面积为(? )
A. 36 B. 26 C. 5 D. 534
设四棱锥P?ABCD的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α?(????)
A. 有无数多个 B. 恰有4个 C. 只有1个 D. 不存在
(多选题)如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则下列说法正确的是(????)
EF//HG B. EH//FG
C. 四边形EFGH为平行四边形 D. 四边形EFGH为梯形
二.填空题
已知平面α?//平面β,点P是平面α,β外一点,直线l与直线m交于点P,且直线l分别与α,β交于点A,B,直线m分别与α,β交于点C,D,若PA=4,PB=5,PC=3,则PD=________.
如图,在长方体ABCD—A1B1C1D1中,过BB1的中点E作一个与平面ACB1平行的平面交AB于点M,交BC于点N,则MNAC=____.
在长方体ABCD?A1B1C1D1中,E为棱DD1上的点.当平面AB1C?//平面A1EC1时,点E的位置是________.
已知平面α//平面β,点A,C∈α,点B,D∈β,直线AB,CD交于点S,且SA=8,SB=9,CD=34.
(1)若点S在平面α,β之间,则SC=??????????;
(2)若点S不在平面α,β之间,则SC=??????????.
在棱长为2的正方体ABCD?A1B1C1D1中,E是DD1的中点,P是正方体ABCD?A1B1C1D1表面上一动点,若B1P?//平面A1C1E,则P点轨迹的长度等于________.
三.解答题
如图,在矩形ABCD和矩形ABEF中,AF=AD,M,N分别在AE,BD上,且AM=DN,矩形ABEF可沿AB任意翻折.
(1)求证:当点F,A,D不共线时,MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,MN总与FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
如图,在四面体ABCD中,过棱AB上一点E作平行于AD和BC的平面,分别交四面体的棱BD,DC,CA于点F,G,H.
(1)求证:四边形EFGH为平行四边形;
(2)若P,Q分别在BD,AC上,DPBD=AQAC=14,且P,F不重合,证明:PQ?//平面EFGH.
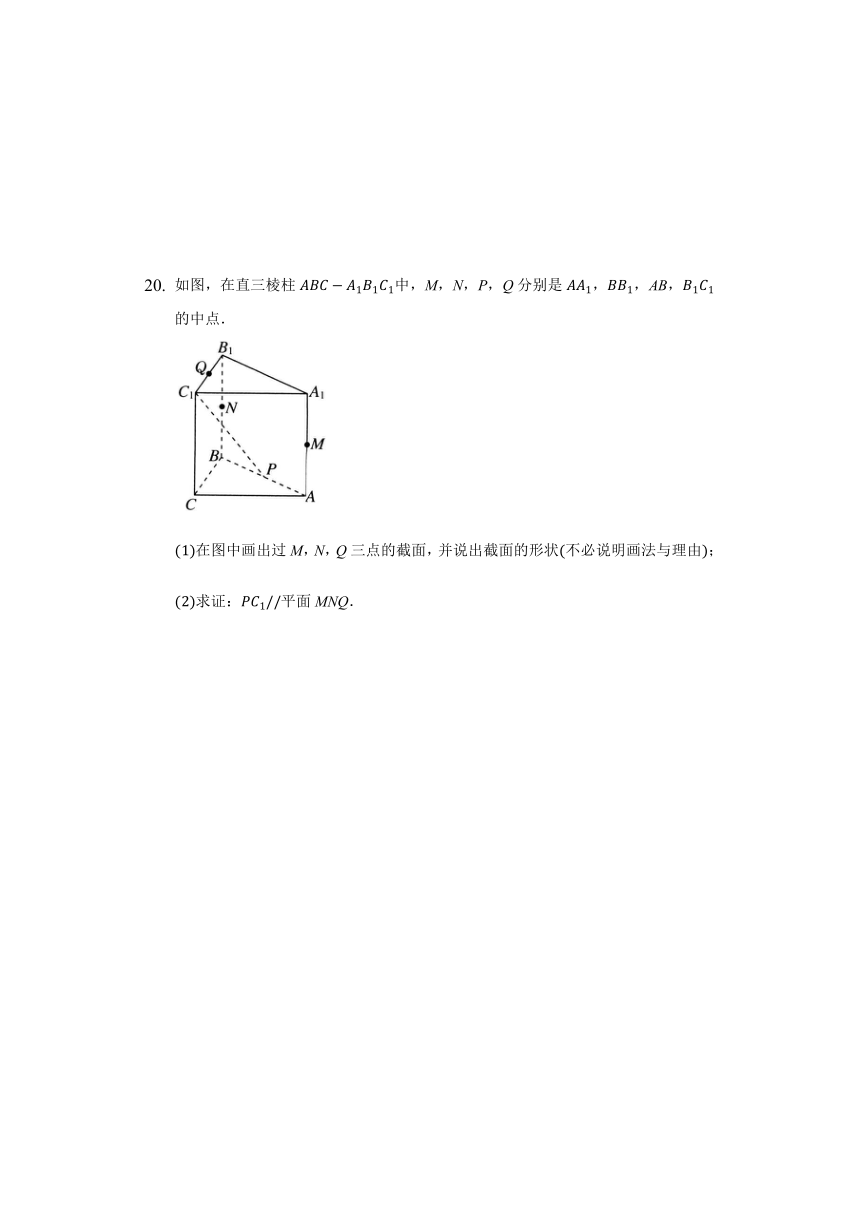
如图,在直三棱柱ABC?A1B1C1中,M,N,P,Q分别是AA1,BB1,AB,B1C1的中点.
(1)在图中画出过M,N,Q三点的截面,并说出截面的形状(不必说明画法与理由);
(2)求证:PC1//平面MNQ.
答案和解析
1.【答案】A
【解析】
【分析】
本题主要考查面面平行的性质定理,基础题.
根据面面平行的性质定理判断即可.
【解答】?
解:根据面面平行的性质定理:若两个平行平面与第三个平面相交,则交线平行,由此可得四条交线两两平行.
故选A.
2.【答案】D
【解析】解:因为平面α//平面β,要使直线AC//直线BD,则直线AC与BD是共面直线,
即A,B,C,D四点必须共面.
故选:D.
利用线面平行的性质以及直线平行的判断条件进行求解.
本题主要考查面面平行的性质以及直线平行的判断条件,比较基础.
3.【答案】A
【解析】
【分析】
本题考查平面与平面平行的性质定理,平行公理和直线与直线的位置关系,属于基础题.
由平面与平面平行的性质定理如果一个平面与两个平行平面都相交那么它们的交线互相平行可得a//c,a//b,a//d再由平行公理可得b//c,b//d,c//d故a?//?b?//?c?//?d
【解答】
解:∵平面α?//平面β,α∩γ=a,β∩γ=c
∴a//c.同理可证a//b,a//d.
由平行公理得a?//?b?//?c?//?d.
故选A.
4.【答案】A
【解析】
【分析】
本题考查线面平行和面面平行的性质定理,属于一道基础题.
取DG的中点为M,连接AM,FM,如图所示.则由已知条件易证四边形DEFM是平行四边形,
得到DE=?//FM,进而根据面面平行的性质定理得到AB//FM,并结合AB=DE,得到四边形ABFM是平行四边形,可得BF//AM,再通过线面平行的判定定理,即可得到结论.
【解答】
解:取DG的中点为M,连接AM,FM,如图所示.则由已知条件易证四边形DEFM是平行四边形,
∴DE=?//FM,
∵平面ABC//平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,
∴AB//DE,
∴AB//FM.又AB=DE
∴AB=FM,
∴四边形ABFM是平行四边形,则BF//AM.又BF?平面ACGD,
∴BF//平面ACGD.
故选A.
5.【答案】D
【解析】
【分析】本题考查了线面平行的性质和中位线定理,以及平行线的性质,属于基础题.
如图,连接AC交BD于点O,连接CN交BM于点,由题意可得G为CN的中点,作HN//BM,可得PH=HC,即可求出答案.
【解答】
解:如图,连接AC,设AC交BD于点O,连接CN,设CN交BM于点G,连接OG.
由AN//平面BDM,平面ANC∩平面BDM=OG,AN?平面ANC,可得AN//OG,
∵OA=OC,∴NG=CG,∴G为CN的中点.
在△PBC中,作HN//BM,设HN∩PC=H,易知M为CH的中点,∴CM=HM,
∵PM∶MC=3∶1,∴PH=HC,
∴PN∶NB=PH∶HM=2∶1,
故选D.
6.【答案】D
【解析】解:设AB、A1B1、A1D1、AD的中点分别为E、F、G、H,连接EF、FG、GH、HE、EG、FH,
∵平面EFGH//平面DBB1D1,EF、FG、GH、HE、EG、FH都是平面EFGH内的直线
∴EF、FG、GH、HE、EG、FH都与平面平面DBB1D1平行,共6条直线,
同理,在平面DBB1D1的另一侧也存在6条直线与平面平面DBB1D1平行,
因此,满足条件:“与平面DBB1D1平行的直线共有”的直线一共有12条.
故选:D.
在平面DBB1D1的一侧,AB、A1B1、A1D1、AD的中点分别为E、F、G、H,根据面面平行的性质可得这四个点的连线有6条都与平面平面DBB1D1平行;
同理在平面DBB1D1的另一侧也存在6条直线与平面平面DBB1D1平行.
本题考查了平行六面体的性质和空间平行位置关系的判定等知识,是基础题.
7.【答案】C
【解析】
【分析】
本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.
【解答】
解:由α、β、γ为三个不重合的平面,a、b、c为三条不同直线,知:
①a//bb//c?a//b,由平行公理知①正确;
②a//γb//γ?a//b,a与b相交或a与b异面,故②错误;
③a//cβ//c?α//β或α与β相交,故③错误;
④a//γβ//γ?α//β,由平面与平面平行的判定定理得④正确;
?⑤a//cα//c?α//a或a?α,故⑤错误;
⑥a//γα//γ??a//α或a?α,故⑥错误.
故选C.
8.【答案】B
【解析】
【分析】
本题考查面面平行的性质,属于基础题.
由面面平行得到△A′B′C′∽△ABC,再由相似三角形得到面积比为相似比的平方,即可得到面积比.
【解答】
解:由题意知,∵平面α//平面ABC,AB?平面ABC,
∴AB//平面α,
又由平面α∩平面PAB=A′B′,则A′B′//AB,
∵PA′:AA′=2:3,即PA′:PA=2:5,
∴A′B′:AB=2:5,
由于相似三角形得到面积比为相似比的平方,
所以S△A′B′C′:S△ABC=4:25.
故选B.
9.【答案】D
【解析】
【分析】
本题考查棱台上、下比值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
设E为CD的中点,G为EC的中点,连接MG,NG,C′E,则NG//AD,平面MNG//平面ADD′A′,推导出MG//DD′.从而E位CD的中点,G为EC的中点,M为CC′的中点,进而DD′//C′E//MG.由此能求出棱台上下底面边长的比值.
【解答】
解:设E为CD的中点,G为EC的中点,
连接MG,NG,C′E,则NG//AD,
则平面MNG//平面ADD′A′,
又平面DCC′D′分别交平面MNG和平面ADD′A′于直线MG,DD′,则MG//DD′.
因为E为CD的中点,G为EC的中点,
M为CC′的中点,所以DD′//C′E//MG.
所以DEC′D′为平行四边形,棱台上下底面边长的比值为12.
故选:D.
10.【答案】B
【解析】
【分析】
本题考查正方体的结构特征,平面的定义和性质,属基础题.
根据已知判定四边形AEC1F就是正方体ABCD?A1B1C1D1被平面α截得的截面,然后计算面积即可.
【解答】
解:延长C1P与BC交于点E,则点E为BC中点,
连接AE,取A1D1中点F,连接AF,C1F,
则四边形AEC1F就是正方体ABCD?A1B1C1D1被平面α截得的截面,
四边形AEC1F是边长为5的菱形,
连接AC1,EF,所以AC1⊥EF,且AC1=23,EF=22,
所以四边形AEC1F的面积为26,
故选B.
11.【答案】A
【解析】
【分析】
本题主要考查棱锥的结构特征、面面平行的性质定理等基础知识,考查了转化思想,属于基础题.
若要使截面四边形A1B1C1D1是平行四边形,我们只要证明A1B1//C1D1,同时A1D1//B1C1即可,根据已知中侧面PAD与侧面PBC相交,侧面PAB与侧面PCD相交,根据面面平行的性质定理,我们易得结论.
【解答】
解:由题知平面PAD与平面PBC相交,平面PAB与平面PCD相交,
可设两组相交平面的交线分别为m,n,
易知m∩n=P.
设m,n确定的平面为β,作α?//?β,
设α与侧棱PA,PB,PC,PD的交点分别为A1,B1,C1,D1,
如图,则由平面与平面平行的性质定理得A1D1?//?m?//?B1C1,A1B1?//?n?//?C1D1,
所以所得截面必为平行四边形.
由于平面α可以上下平移,可知满足条件的平面α有无数多个.
故选A.
12.【答案】ABC
【解析】
【分析】
本题考查简单多面体及其结构特征以及空间中直线与直线的位置关系的问题,是基础题。
根据题意多面体及其结构特征对各项进行判断即可.
【解答】
解∵平面ABFE?//平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF?//?HG,同理,EH?//?FG,所以四边形EFGH为平行四边形.
故答案选ABC.
13.【答案】154
【解析】
【分析】
本题考查了面面平行的性质,由题意证明AC//BD?然后结合平行线截线段成比例求得PD的长度.
【解答】
解:连接AC,BD,由题意及面面平行的性质知AC?//?BD,
所以△PAC∽△PBD,所以PAPB=PCPD,所以PD=PC?PBPA=3×54=154.
故答案为154.
14.【答案】12
【解析】
【分析】
本题考查面面平行的性质定理,属基础题.根据面面平行得线线平行,从而证明MN是ΔABC的中位线即可得.
【解答】
解:因为平面ACB1?//平面MNE,
所以ME?//AB1,
因为E是BB1的中点,
所以M是AM中点.
同理可得N是BC的中点,
所以MN是ΔABC的中位线,
即MN?//AC,且MN=12AC,
故MNAC=12.
故答案为12.
15.【答案】与D重合
【解析】
【分析】
本题考查平面与平面平行的性质定理,属于基础题.
由平面与平面平行的性质定理,结合题设条件容易确定点E的位置.
【解答】
证明:如右图示连接B1D1,BD,设B1D1∩A1C1=M,BD∩AC=O,连接ME,MD,B1O.
∵平面AB1C?//平面A1EC1,
平面AB1C∩平面BDD1B1=B1O,平面A1EC1∩平面BDD1B1=ME,
∴B1O?//?ME,
又四边形B1MDO为平行四边形,
∴B1O?//?MD,
∴点E与点D重合.
16.【答案】(1)16;
(2)272.
【解析】
【分析】
本题考查面面平行的性质的应用,以及平行线分线段成比例,属于中档题.
(1)由面面平行的性质定理得AC//BD,由平行线分线段成比例定理得SASB=SCSD,代入求值;
(2)由面面平行的性质定理得AC//BD,由平行线分线段成比例定理得SASB=SCSD,代入求值.
【解答】
解:(1)因为AB∩CD=S,所以AB,CD确定一个平面,设为γ,则α∩γ=AC,β∩γ=BD.
因为α//β,
所以AC//BD.
于是SASB=SCSD,即89=SC34?SC,
所以SC=16.
(2)同(1)得AC//BD,
则SASB=SCSD,即89=SCSC+34,
解得SC=272.
故答案为16;272.
17.【答案】45
【解析】
【分析】
本题考查了空间中的距离,点的轨迹,属于中档题.
由题意画出图形,利用已知条件,判断P的轨迹,然后求解轨迹长度.
【解答】
解:∵P是正方体ABCD?A1B1C1D1表面上一动点,B1P?//平面A1C1E,
∴当点P运动时,B1P所在的平面与平面A1C1E平行.
由平面与平面平行的性质定理知B1P所在的平面为平面B1MDN,
如图所示,
其中M,N分别为CC1,AA1的中点,
∴P点的轨迹为四边形B1MDN(不含点B1),
易得DM=DN=NB1=B1M=5,
故P点轨迹的长度为45.
故答案为45.
18.【答案】(1)证明:在平面图形中,设MN交AB于点G,
由于四边形ABCD和四边形ABEF都是矩形且AD=AF,从而有AD//BE且AD=BE,
∴四边形ADBE是平行四边形,
∴AE//DB.
∵AM=DN,
∴MN//AD.
矩形ABEF沿AB翻折后,当F,A,D不共线时,如图①,连接FD,EC,MN,
易知MG//AF,NG//AD,MG∩NG=G,AD∩AF=A,
∴平面ADF//平面GNM.
又∵MN?平面GNM,
∴MN//平面ADF.
∴当F,A,D不共线时,MN总平行于平面FAD.
(2)解:这个结论不正确.
要使所给结论正确,M,N应分别为AE和DB的中点.
理由如下:当F,A,D共线时,矩形ABEF不翻折,易证得FD//MN.
当F,A,D不共线时,由(1)知平面MNG//平面FDA,
根据面面平行的性质定理,可知要使MN//FD总成立,只要FD与MN共面即可.
若要使FD与MN共面,连接FM,只要直线FM与直线DN相交即可.
结合题意,应使直线DN与直线FM相交于点B,这样M,N分别为AE,DB的中点,如图②.
∵FM∩DN=B,
∴FM,DN确定平面FDNM,
又∵平面FDNM∩平面MNG=MN,平面FDNM∩平面FDA=FD,平面MNG//平面FDA,
∴MN//FD.
【解析】本题主要考查了空间线面位置关系,要求熟练掌握相应的定义和定理,注意定理成立的条件,属于基本知识的考查.
(1)由题意可知AF//MG,GN//AD,可证平面MNG//平面FAD,MN?平面GMN,从而得证.
(2)要使所给结论正确,M,N应分别为AE和DB的中点.
理由如下:当F,A,D共线时,矩形ABEF不翻折,易证得FD//MN.当F,A,D不共线时,利用(1)的结论以及面面平行的性质求解.
19.【答案】证明:(1)∵AD//平面EFGH,平面ADB∩平面EHGH=EF,AD?平面ABD,
∴AD//EF,
∵AD//平面EHGH,平面ADC∩平面EHGH=GH,AD?平面ADC,
∴AD//GH,
由平行公理可得:EF//GH,同理可得EH//FG,
∴四边形EFGH为平行四边形.
(2)如图在CD上取点M,使DPBD=DMDC=14,
连接MQ,则PM//BC//FG,
由AQAC=DMDC=14,则QM//AD//HG,
又PM∩QM=M,
∴平面PMQ//平面EHGH,
∵PQ?平面PMQ,
∴PQ//截面EFGH.
【解析】(1)利用线面平行的性质可证AD//EF,AD//GH,由平行公理可得:EF//GH,同理可得EH//FG,即可得证;
(2)在CD上取点M,使DPBD=DMDC=14,连接MQ,则结合已知可得QM//AD//HG,利用面面平行的判断定理可证平面PMQ//平面EHGH,利用面面平行的性质可得PQ//截面EFGH.
本题考查线面平行的判定,面面平行的判定以及线面平行性质的运用,考查学生分析解决问题的能力,属于中档题.
20.【答案】解:(1)如右图所示:取A1C1的中点H,连接HQ,QN,NM,MH
则梯形MHQN是过M,N,Q三点的截面.
(2)证明:连接BC1,AC1.
∵三棱柱ABC?A1B1C是直三棱柱,
∴四边形ABB1A1是矩形.
在矩形ABB1A1中:
∵M,N分别是AA1,BB1的中点,
∴MN?//?AB.
∵MN?平面ABC1,AB?平面ABC1,
∴MN?//平面ABC1.
?在△B1C1B中:
∵Q,N分别是B1C1,BB1的中点,
∴NQ?//?BC1.
∵QN?平面ABC1,BC1?平面ABC1,
∴QN?//平面ABC1.?
又∵MN∩QN=N,
∴平面MNQ?//平面ABC1.
∵P是AB的中点,∴PC1?平面ABC1.
故PC1?//平面MNQ.
【解析】
【分析】
本题考查空间几何体中截面的作法及直线与平面平行的判定,属于中档题.
(1)由题在矩形ABB1A1中:
∵M,N分别是AA1,BB1的中点,
∴MN?//?A1B1.
∵A1B1?平面MQN,MN?平面MQN,
∴A1B1//平面MNQ.
∵A1B1?平面A1B1C1
平面A1B1C1?平面MNQ且Q为公共点,,
∴A1B1平行与平面A1B1C1?平面MNQ的交线,
又因为Q是所在边的中点,
故取A1C1的中点H,连接HQ,QN,NM,MH则梯形MHQN是过M,N,Q三点的截面.
(2)结合题设条件应用直线与平面平行的判定定理证得MN?//平面ABC1,QN?//平面ABC1,再由平面与平面平行的判定定理证得平面MNQ?//平面ABC1,最后由平面与平面平行的性质定理即可证得PC1?//平面MNQ
学校:___________姓名:___________班级:___________学号:___________
一.选择题
两个平行平面与另两个平行平面相交所得四条直线的位置关系是(????)
A. 两两互相平行 B. 两两相交于同一点
C. 两两相交但不一定交于同一点 D. 两两互相平行或交于同一点
平面α//平面β,点A,C∈α,B,D∈β,则直线AC//直线BD的充要条件是(????)
A. AB//CD B. AD//CB
C. AB与CD相交 D. A,B,C,D四点共面
若平面α?//平面β,平面γ?//平面δ,且α∩γ=a,α∩δ=b,β∩γ=c,β∩δ=d,则交线a,b,c,d的位置关系是(????)
A. 互相平行 B. 交于一点 C. 互相异面 D. 不能确定
如图,在多面体ABCDEFG中,平面ABC?//平面DEFG,EF?//DG,AB=DE,DG=2EF,则(????)
A. BF//平面ACGD
B. CF//平面ABED
C. BC//FG
D. 平面ABED//平面CGF
如图,四棱锥P?ABCD的底面ABCD是平行四边形,M,N分别为棱PC,PB上的点,若PM∶MC=3∶1,且AN//平面BDM,则PN∶NB=?(????)?
A. 4∶1 B. 3∶1
C. 3∶2 D. 2∶1
已知四棱柱ABCD?A1B1C1D1的底面是平行四边形,过此四棱柱任意两条棱的中点作直线,其中与平面DBB1D1平行的直线共有? (??? )
A. 4条 B. 6条 C. 10条 D. 12条
α,β,γ为三个不重合的平面,a,b,c为三条不同的直线,则下列命题中不正确的是(????)
①a//cb//c?a//b;②a//γb//γ?a//b;③α//cβ//c?α//β;
④α//γβ//γ?α//β;⑤α//ca//c?α//a;⑥α//γa//γ?a//α.
A. ④⑥ B. ②③⑥ C. ②③⑤⑥ D. ②③
如图所示,P是三角形ABC所在平面外一点,平面α//平面ABC,α分别交线段PA,PB,PC于A′,B′,C′,若PA′:AA′=2:3,则S△A′B′C′:S△ABC=(????)
A. 2:25 B. 4:25
C. 2:5 D. 4:5
如图所示,四棱台ABCD?A′B′C′D′的底面为正方形,M为CC′的中点,点N在线段AB上,且AB=4BN.若MN?//平面ADD′A′,则此棱台上、下底面边长的比值为(????)
A. 15 B. 14
C. 13 D. 12
已知正方体ABCD?A1B1C1D1的棱长为2,点P在线段CB1上,且B1P=2PC,平面α经过点A,P,C1,则正方体ABCD?A1B1C1D1被平面α截得的截面面积为(? )
A. 36 B. 26 C. 5 D. 534
设四棱锥P?ABCD的底面不是平行四边形,用平面α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α?(????)
A. 有无数多个 B. 恰有4个 C. 只有1个 D. 不存在
(多选题)如图是长方体被一平面所截得的几何体,四边形EFGH为截面,则下列说法正确的是(????)
EF//HG B. EH//FG
C. 四边形EFGH为平行四边形 D. 四边形EFGH为梯形
二.填空题
已知平面α?//平面β,点P是平面α,β外一点,直线l与直线m交于点P,且直线l分别与α,β交于点A,B,直线m分别与α,β交于点C,D,若PA=4,PB=5,PC=3,则PD=________.
如图,在长方体ABCD—A1B1C1D1中,过BB1的中点E作一个与平面ACB1平行的平面交AB于点M,交BC于点N,则MNAC=____.
在长方体ABCD?A1B1C1D1中,E为棱DD1上的点.当平面AB1C?//平面A1EC1时,点E的位置是________.
已知平面α//平面β,点A,C∈α,点B,D∈β,直线AB,CD交于点S,且SA=8,SB=9,CD=34.
(1)若点S在平面α,β之间,则SC=??????????;
(2)若点S不在平面α,β之间,则SC=??????????.
在棱长为2的正方体ABCD?A1B1C1D1中,E是DD1的中点,P是正方体ABCD?A1B1C1D1表面上一动点,若B1P?//平面A1C1E,则P点轨迹的长度等于________.
三.解答题
如图,在矩形ABCD和矩形ABEF中,AF=AD,M,N分别在AE,BD上,且AM=DN,矩形ABEF可沿AB任意翻折.
(1)求证:当点F,A,D不共线时,MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,MN总与FD平行”这个结论正确吗?如果正确,请证明;如果不正确,请说明能否改变个别已知条件使上述结论成立,并给出理由.
如图,在四面体ABCD中,过棱AB上一点E作平行于AD和BC的平面,分别交四面体的棱BD,DC,CA于点F,G,H.
(1)求证:四边形EFGH为平行四边形;
(2)若P,Q分别在BD,AC上,DPBD=AQAC=14,且P,F不重合,证明:PQ?//平面EFGH.
如图,在直三棱柱ABC?A1B1C1中,M,N,P,Q分别是AA1,BB1,AB,B1C1的中点.
(1)在图中画出过M,N,Q三点的截面,并说出截面的形状(不必说明画法与理由);
(2)求证:PC1//平面MNQ.
答案和解析
1.【答案】A
【解析】
【分析】
本题主要考查面面平行的性质定理,基础题.
根据面面平行的性质定理判断即可.
【解答】?
解:根据面面平行的性质定理:若两个平行平面与第三个平面相交,则交线平行,由此可得四条交线两两平行.
故选A.
2.【答案】D
【解析】解:因为平面α//平面β,要使直线AC//直线BD,则直线AC与BD是共面直线,
即A,B,C,D四点必须共面.
故选:D.
利用线面平行的性质以及直线平行的判断条件进行求解.
本题主要考查面面平行的性质以及直线平行的判断条件,比较基础.
3.【答案】A
【解析】
【分析】
本题考查平面与平面平行的性质定理,平行公理和直线与直线的位置关系,属于基础题.
由平面与平面平行的性质定理如果一个平面与两个平行平面都相交那么它们的交线互相平行可得a//c,a//b,a//d再由平行公理可得b//c,b//d,c//d故a?//?b?//?c?//?d
【解答】
解:∵平面α?//平面β,α∩γ=a,β∩γ=c
∴a//c.同理可证a//b,a//d.
由平行公理得a?//?b?//?c?//?d.
故选A.
4.【答案】A
【解析】
【分析】
本题考查线面平行和面面平行的性质定理,属于一道基础题.
取DG的中点为M,连接AM,FM,如图所示.则由已知条件易证四边形DEFM是平行四边形,
得到DE=?//FM,进而根据面面平行的性质定理得到AB//FM,并结合AB=DE,得到四边形ABFM是平行四边形,可得BF//AM,再通过线面平行的判定定理,即可得到结论.
【解答】
解:取DG的中点为M,连接AM,FM,如图所示.则由已知条件易证四边形DEFM是平行四边形,
∴DE=?//FM,
∵平面ABC//平面DEFG,平面ABC∩平面ADEB=AB,平面DEFG∩平面ADEB=DE,
∴AB//DE,
∴AB//FM.又AB=DE
∴AB=FM,
∴四边形ABFM是平行四边形,则BF//AM.又BF?平面ACGD,
∴BF//平面ACGD.
故选A.
5.【答案】D
【解析】
【分析】本题考查了线面平行的性质和中位线定理,以及平行线的性质,属于基础题.
如图,连接AC交BD于点O,连接CN交BM于点,由题意可得G为CN的中点,作HN//BM,可得PH=HC,即可求出答案.
【解答】
解:如图,连接AC,设AC交BD于点O,连接CN,设CN交BM于点G,连接OG.
由AN//平面BDM,平面ANC∩平面BDM=OG,AN?平面ANC,可得AN//OG,
∵OA=OC,∴NG=CG,∴G为CN的中点.
在△PBC中,作HN//BM,设HN∩PC=H,易知M为CH的中点,∴CM=HM,
∵PM∶MC=3∶1,∴PH=HC,
∴PN∶NB=PH∶HM=2∶1,
故选D.
6.【答案】D
【解析】解:设AB、A1B1、A1D1、AD的中点分别为E、F、G、H,连接EF、FG、GH、HE、EG、FH,
∵平面EFGH//平面DBB1D1,EF、FG、GH、HE、EG、FH都是平面EFGH内的直线
∴EF、FG、GH、HE、EG、FH都与平面平面DBB1D1平行,共6条直线,
同理,在平面DBB1D1的另一侧也存在6条直线与平面平面DBB1D1平行,
因此,满足条件:“与平面DBB1D1平行的直线共有”的直线一共有12条.
故选:D.
在平面DBB1D1的一侧,AB、A1B1、A1D1、AD的中点分别为E、F、G、H,根据面面平行的性质可得这四个点的连线有6条都与平面平面DBB1D1平行;
同理在平面DBB1D1的另一侧也存在6条直线与平面平面DBB1D1平行.
本题考查了平行六面体的性质和空间平行位置关系的判定等知识,是基础题.
7.【答案】C
【解析】
【分析】
本题考查命题真假的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.
【解答】
解:由α、β、γ为三个不重合的平面,a、b、c为三条不同直线,知:
①a//bb//c?a//b,由平行公理知①正确;
②a//γb//γ?a//b,a与b相交或a与b异面,故②错误;
③a//cβ//c?α//β或α与β相交,故③错误;
④a//γβ//γ?α//β,由平面与平面平行的判定定理得④正确;
?⑤a//cα//c?α//a或a?α,故⑤错误;
⑥a//γα//γ??a//α或a?α,故⑥错误.
故选C.
8.【答案】B
【解析】
【分析】
本题考查面面平行的性质,属于基础题.
由面面平行得到△A′B′C′∽△ABC,再由相似三角形得到面积比为相似比的平方,即可得到面积比.
【解答】
解:由题意知,∵平面α//平面ABC,AB?平面ABC,
∴AB//平面α,
又由平面α∩平面PAB=A′B′,则A′B′//AB,
∵PA′:AA′=2:3,即PA′:PA=2:5,
∴A′B′:AB=2:5,
由于相似三角形得到面积比为相似比的平方,
所以S△A′B′C′:S△ABC=4:25.
故选B.
9.【答案】D
【解析】
【分析】
本题考查棱台上、下比值的求法,考查空间中线线、线面、面面间的位置关系等基础知识,考查运算求解能力,考查数形结合思想,是中档题.
设E为CD的中点,G为EC的中点,连接MG,NG,C′E,则NG//AD,平面MNG//平面ADD′A′,推导出MG//DD′.从而E位CD的中点,G为EC的中点,M为CC′的中点,进而DD′//C′E//MG.由此能求出棱台上下底面边长的比值.
【解答】
解:设E为CD的中点,G为EC的中点,
连接MG,NG,C′E,则NG//AD,
则平面MNG//平面ADD′A′,
又平面DCC′D′分别交平面MNG和平面ADD′A′于直线MG,DD′,则MG//DD′.
因为E为CD的中点,G为EC的中点,
M为CC′的中点,所以DD′//C′E//MG.
所以DEC′D′为平行四边形,棱台上下底面边长的比值为12.
故选:D.
10.【答案】B
【解析】
【分析】
本题考查正方体的结构特征,平面的定义和性质,属基础题.
根据已知判定四边形AEC1F就是正方体ABCD?A1B1C1D1被平面α截得的截面,然后计算面积即可.
【解答】
解:延长C1P与BC交于点E,则点E为BC中点,
连接AE,取A1D1中点F,连接AF,C1F,
则四边形AEC1F就是正方体ABCD?A1B1C1D1被平面α截得的截面,
四边形AEC1F是边长为5的菱形,
连接AC1,EF,所以AC1⊥EF,且AC1=23,EF=22,
所以四边形AEC1F的面积为26,
故选B.
11.【答案】A
【解析】
【分析】
本题主要考查棱锥的结构特征、面面平行的性质定理等基础知识,考查了转化思想,属于基础题.
若要使截面四边形A1B1C1D1是平行四边形,我们只要证明A1B1//C1D1,同时A1D1//B1C1即可,根据已知中侧面PAD与侧面PBC相交,侧面PAB与侧面PCD相交,根据面面平行的性质定理,我们易得结论.
【解答】
解:由题知平面PAD与平面PBC相交,平面PAB与平面PCD相交,
可设两组相交平面的交线分别为m,n,
易知m∩n=P.
设m,n确定的平面为β,作α?//?β,
设α与侧棱PA,PB,PC,PD的交点分别为A1,B1,C1,D1,
如图,则由平面与平面平行的性质定理得A1D1?//?m?//?B1C1,A1B1?//?n?//?C1D1,
所以所得截面必为平行四边形.
由于平面α可以上下平移,可知满足条件的平面α有无数多个.
故选A.
12.【答案】ABC
【解析】
【分析】
本题考查简单多面体及其结构特征以及空间中直线与直线的位置关系的问题,是基础题。
根据题意多面体及其结构特征对各项进行判断即可.
【解答】
解∵平面ABFE?//平面DCGH,又平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,∴EF?//?HG,同理,EH?//?FG,所以四边形EFGH为平行四边形.
故答案选ABC.
13.【答案】154
【解析】
【分析】
本题考查了面面平行的性质,由题意证明AC//BD?然后结合平行线截线段成比例求得PD的长度.
【解答】
解:连接AC,BD,由题意及面面平行的性质知AC?//?BD,
所以△PAC∽△PBD,所以PAPB=PCPD,所以PD=PC?PBPA=3×54=154.
故答案为154.
14.【答案】12
【解析】
【分析】
本题考查面面平行的性质定理,属基础题.根据面面平行得线线平行,从而证明MN是ΔABC的中位线即可得.
【解答】
解:因为平面ACB1?//平面MNE,
所以ME?//AB1,
因为E是BB1的中点,
所以M是AM中点.
同理可得N是BC的中点,
所以MN是ΔABC的中位线,
即MN?//AC,且MN=12AC,
故MNAC=12.
故答案为12.
15.【答案】与D重合
【解析】
【分析】
本题考查平面与平面平行的性质定理,属于基础题.
由平面与平面平行的性质定理,结合题设条件容易确定点E的位置.
【解答】
证明:如右图示连接B1D1,BD,设B1D1∩A1C1=M,BD∩AC=O,连接ME,MD,B1O.
∵平面AB1C?//平面A1EC1,
平面AB1C∩平面BDD1B1=B1O,平面A1EC1∩平面BDD1B1=ME,
∴B1O?//?ME,
又四边形B1MDO为平行四边形,
∴B1O?//?MD,
∴点E与点D重合.
16.【答案】(1)16;
(2)272.
【解析】
【分析】
本题考查面面平行的性质的应用,以及平行线分线段成比例,属于中档题.
(1)由面面平行的性质定理得AC//BD,由平行线分线段成比例定理得SASB=SCSD,代入求值;
(2)由面面平行的性质定理得AC//BD,由平行线分线段成比例定理得SASB=SCSD,代入求值.
【解答】
解:(1)因为AB∩CD=S,所以AB,CD确定一个平面,设为γ,则α∩γ=AC,β∩γ=BD.
因为α//β,
所以AC//BD.
于是SASB=SCSD,即89=SC34?SC,
所以SC=16.
(2)同(1)得AC//BD,
则SASB=SCSD,即89=SCSC+34,
解得SC=272.
故答案为16;272.
17.【答案】45
【解析】
【分析】
本题考查了空间中的距离,点的轨迹,属于中档题.
由题意画出图形,利用已知条件,判断P的轨迹,然后求解轨迹长度.
【解答】
解:∵P是正方体ABCD?A1B1C1D1表面上一动点,B1P?//平面A1C1E,
∴当点P运动时,B1P所在的平面与平面A1C1E平行.
由平面与平面平行的性质定理知B1P所在的平面为平面B1MDN,
如图所示,
其中M,N分别为CC1,AA1的中点,
∴P点的轨迹为四边形B1MDN(不含点B1),
易得DM=DN=NB1=B1M=5,
故P点轨迹的长度为45.
故答案为45.
18.【答案】(1)证明:在平面图形中,设MN交AB于点G,
由于四边形ABCD和四边形ABEF都是矩形且AD=AF,从而有AD//BE且AD=BE,
∴四边形ADBE是平行四边形,
∴AE//DB.
∵AM=DN,
∴MN//AD.
矩形ABEF沿AB翻折后,当F,A,D不共线时,如图①,连接FD,EC,MN,
易知MG//AF,NG//AD,MG∩NG=G,AD∩AF=A,
∴平面ADF//平面GNM.
又∵MN?平面GNM,
∴MN//平面ADF.
∴当F,A,D不共线时,MN总平行于平面FAD.
(2)解:这个结论不正确.
要使所给结论正确,M,N应分别为AE和DB的中点.
理由如下:当F,A,D共线时,矩形ABEF不翻折,易证得FD//MN.
当F,A,D不共线时,由(1)知平面MNG//平面FDA,
根据面面平行的性质定理,可知要使MN//FD总成立,只要FD与MN共面即可.
若要使FD与MN共面,连接FM,只要直线FM与直线DN相交即可.
结合题意,应使直线DN与直线FM相交于点B,这样M,N分别为AE,DB的中点,如图②.
∵FM∩DN=B,
∴FM,DN确定平面FDNM,
又∵平面FDNM∩平面MNG=MN,平面FDNM∩平面FDA=FD,平面MNG//平面FDA,
∴MN//FD.
【解析】本题主要考查了空间线面位置关系,要求熟练掌握相应的定义和定理,注意定理成立的条件,属于基本知识的考查.
(1)由题意可知AF//MG,GN//AD,可证平面MNG//平面FAD,MN?平面GMN,从而得证.
(2)要使所给结论正确,M,N应分别为AE和DB的中点.
理由如下:当F,A,D共线时,矩形ABEF不翻折,易证得FD//MN.当F,A,D不共线时,利用(1)的结论以及面面平行的性质求解.
19.【答案】证明:(1)∵AD//平面EFGH,平面ADB∩平面EHGH=EF,AD?平面ABD,
∴AD//EF,
∵AD//平面EHGH,平面ADC∩平面EHGH=GH,AD?平面ADC,
∴AD//GH,
由平行公理可得:EF//GH,同理可得EH//FG,
∴四边形EFGH为平行四边形.
(2)如图在CD上取点M,使DPBD=DMDC=14,
连接MQ,则PM//BC//FG,
由AQAC=DMDC=14,则QM//AD//HG,
又PM∩QM=M,
∴平面PMQ//平面EHGH,
∵PQ?平面PMQ,
∴PQ//截面EFGH.
【解析】(1)利用线面平行的性质可证AD//EF,AD//GH,由平行公理可得:EF//GH,同理可得EH//FG,即可得证;
(2)在CD上取点M,使DPBD=DMDC=14,连接MQ,则结合已知可得QM//AD//HG,利用面面平行的判断定理可证平面PMQ//平面EHGH,利用面面平行的性质可得PQ//截面EFGH.
本题考查线面平行的判定,面面平行的判定以及线面平行性质的运用,考查学生分析解决问题的能力,属于中档题.
20.【答案】解:(1)如右图所示:取A1C1的中点H,连接HQ,QN,NM,MH
则梯形MHQN是过M,N,Q三点的截面.
(2)证明:连接BC1,AC1.
∵三棱柱ABC?A1B1C是直三棱柱,
∴四边形ABB1A1是矩形.
在矩形ABB1A1中:
∵M,N分别是AA1,BB1的中点,
∴MN?//?AB.
∵MN?平面ABC1,AB?平面ABC1,
∴MN?//平面ABC1.
?在△B1C1B中:
∵Q,N分别是B1C1,BB1的中点,
∴NQ?//?BC1.
∵QN?平面ABC1,BC1?平面ABC1,
∴QN?//平面ABC1.?
又∵MN∩QN=N,
∴平面MNQ?//平面ABC1.
∵P是AB的中点,∴PC1?平面ABC1.
故PC1?//平面MNQ.
【解析】
【分析】
本题考查空间几何体中截面的作法及直线与平面平行的判定,属于中档题.
(1)由题在矩形ABB1A1中:
∵M,N分别是AA1,BB1的中点,
∴MN?//?A1B1.
∵A1B1?平面MQN,MN?平面MQN,
∴A1B1//平面MNQ.
∵A1B1?平面A1B1C1
平面A1B1C1?平面MNQ且Q为公共点,,
∴A1B1平行与平面A1B1C1?平面MNQ的交线,
又因为Q是所在边的中点,
故取A1C1的中点H,连接HQ,QN,NM,MH则梯形MHQN是过M,N,Q三点的截面.
(2)结合题设条件应用直线与平面平行的判定定理证得MN?//平面ABC1,QN?//平面ABC1,再由平面与平面平行的判定定理证得平面MNQ?//平面ABC1,最后由平面与平面平行的性质定理即可证得PC1?//平面MNQ
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
