2020-2021学年高一下学期数学人教A版(2019)必修第二册第六章 6.1 平面向量的概念 同步练习Word含解析
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版(2019)必修第二册第六章 6.1 平面向量的概念 同步练习Word含解析 |  | |
| 格式 | docx | ||
| 文件大小 | 230.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 12:26:15 | ||
图片预览




文档简介
2020-2021学年高一数学人教A版(2019)必修第二册
6.1 平面向量的概念 同步练习
班级 姓名 学号
一.选择题
下列说法中错误的是(????)
A. 零向量与任一向量平行
B. 方向相反的两个非零向量不一定共线
C. 零向量的长度为0
D. 方向相反的两个非零向量必不相等
设a,b为非零向量,则“a//b”是“a,b的方向相同”的? (??? )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
如图,设O是正六边形ABCDEF的中心,则与BC相等的向量为? (??? )
A. BA
B. CD
C. AD
D. OD
给出下列命题:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量AB与BA相等.则所有正确命题的序号是(????)
A. ① B. ③ C. ①③ D. ①②
已知向量a,b是两个非零向量,AO,BC分别是与a,b同方向的模为1的向量,则下列各式一定正确的是? (??? )
A. AO=BO B. AO=BO或AO=?BO
C. AO=1 D. |AO|=|BO|
如图所示,设O是正方形ABCD的中心,则下列结论正确的有____.(填序号)
? ①AO=OC; ②AO//AC; ③AB与CD共线; ④AO=BO.
已知集合A={与a共线的向量},B={与a长度相等的向量},C={与a长度相等、方向相反的向量},其中a为非零向量,则下列结论中错误的是? (??? )
A. C?A B. A?B={a} C. C?B D. A∩B?{a}
如图,在等腰梯形ABCD中,对角线AC与BD交于点P,点E,F分别在两腰AD,BC上,EF过点P,且EF//AB,则下列等式中成立的是(? ? ? ?)
A. AD=BC
B. AC=BD
C. PE=PF
D. EP=PF
已知向量AB与向量BC共线,下列关于向量AC的说法中,正确的是? (??? )
A. 向量AC与向量AB一定同向 B. 向量BC,AB,AC一定共线
C. 向量AC与向量BC一定相等 D. 以上说法都不正确
如图,网格纸上小正方形的边长为1,D,E分别是△ABC的边AB,AC的中点,则(? ? ?)
A. |AB|=5且|BC|=2.5|DE|
B. |AB|=5且|BC|=2|DE|
C. |AB|=6且|BC|=2|DE|
D. |AB|=6且|BC|=3|DE|
二.填空题
给出下列说法:
①两个向量,当且仅当它们的起点相同、终点相同时才相等;
②若AB=DC,则A,B,C,D为平行四边形的四个顶点;
③若四边形ABCD为平行四边形,则AB=DC;
④若a≠b,则a与b一定不共线.
其中正确说法的序号是____.
如图,O是正三角形ABC的中心,四边形AOCD和AOBE均为平行四边形,则与向量AD相等的向量为??????????;与向量OA共线的向量为??????????_;与向量OA的模相等的向量为??????????.(填图中所画出的向量)
已知在四边形ABCD中,BC=AD且|AB|=|BD|=|BC|=2,则四边形ABCD的内切圆的面积是_______.
若在一个边长为5的正三角形ABC中,一个向量所对应的有向线段为AD(其中D在边BC上运动),则向量AD的模的最小值为________.
三.解答题
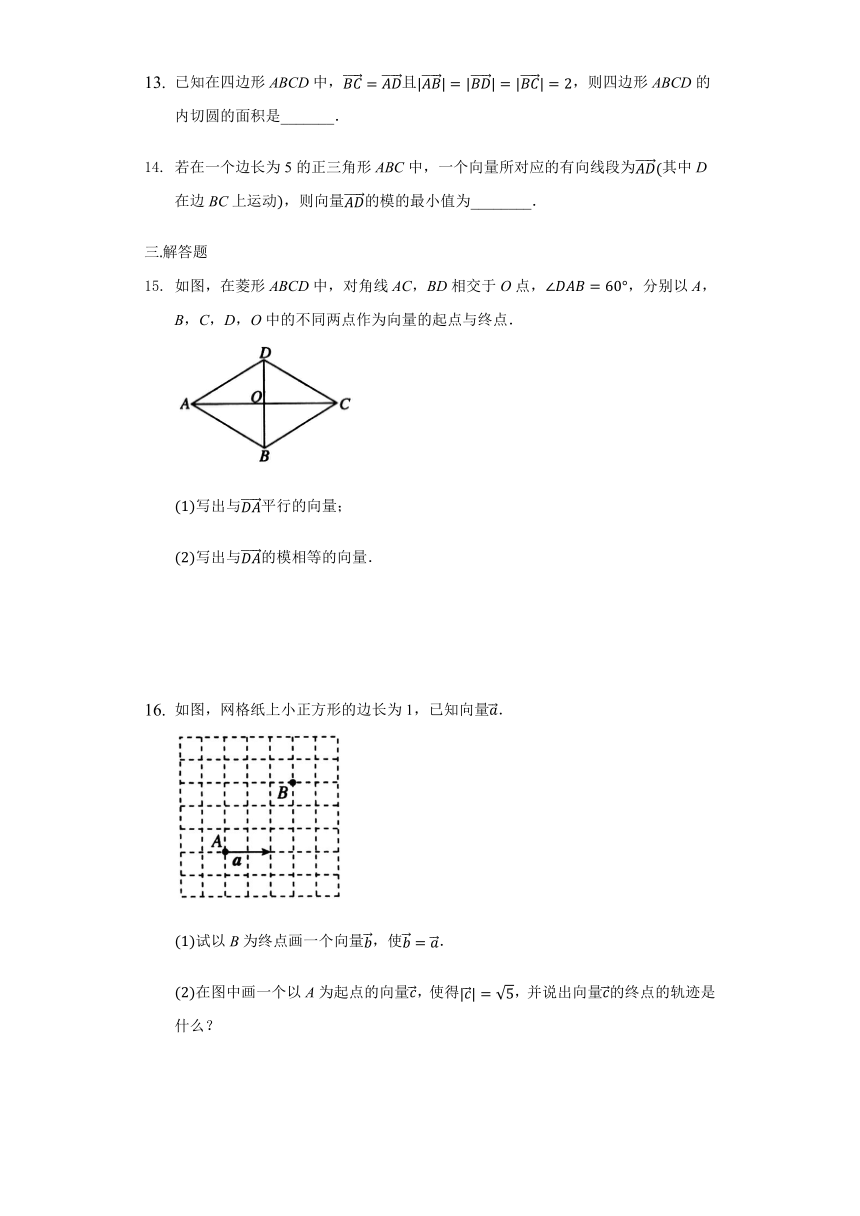
如图,在菱形ABCD中,对角线AC,BD相交于O点,∠DAB=60°,分别以A,B,C,D,O中的不同两点作为向量的起点与终点.
(1)写出与DA平行的向量;
(2)写出与DA的模相等的向量.
如图,网格纸上小正方形的边长为1,已知向量a.
(1)试以B为终点画一个向量b,使b=a.
(2)在图中画一个以A为起点的向量c,使得|c|=5,并说出向量c的终点的轨迹是什么?
如图,已知四边形ABCD中,M,N分别是BC,AD上的点,AB=DC且CN=MA,求证:DN=MB.
一辆消防车从A地去B地执行任务,先从A地向北偏东30°方向行驶2千米到达D地,然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.
(1)在图中画出AD,DC,CB,AB;
(2)求B地相对于A地的位移.
答案和解析
1.【答案】B
【解析】
【分析】
本题考查了平面向量的基本概念,是基础题.
根据平面向量的基本概念,分析正误即可.
【解答】
解:对于A,零向量的方向是任意的,
零向量与任一向量平行,A正确;
对于B,方向相反的两个非零向量一定共线,B错误;
对于C,零向量的模长为0,C正确;
对于D,根据向量相等的定义知,方向相反的两个非零向量一定不相等,D正确.
故选:B.
2.【答案】B
【解析】
【分析】
本题考查充分条件、必要条件的判定方法,考查向量共线的概念,属于基础题.
由充分条件、必要条件的判定方法及向量共线的概念分析得答案.
【解答】
解:对于非零向量a,b,由a//b可得:a与b方向相同或相反,
反之,a与b方向相同?a//b,
则“a//b”是“a与b方向相同”的必要不充分条件.
故选B.
3.【答案】D
【解析】
【分析】
本题主要考查向量相等的定义,属于基础题.
由向量相等的定义,模相等,方向相同即可求解.
【解答】
解:根据图形可知四边形BCDO是平行四边形,∴BC?//?OD,BC=OD,∴BC=OD,
故选D.
4.【答案】A
【解析】
【分析】
本题主要考查向量的基本概念,属于基础题.
根据零向量、单位向量、相等向量的概念可一一判断.
【解答】
解:根据零向量的定义可知①正确;
根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;
向量AB与BA互为相反向量,故③错误.
故选A.
5.【答案】D
【解析】
【分析】
本题考查向量的有关概念,属基础题,
由a,b只是模相等,方向不一定相同,可判断.
【解答】
解:由于a与b的方向不知,故AO与BO无法判断是否相等,故A、B选项均错.
又AO与BO均为单位向量,∴|AO|=|BO|,故C错,D对.
故选D.
6.【答案】①②③
【解析】
【分析】
本题考查了平面向量相等与共线定理的应用问题,是基础题.根据题意画出图形,结合图形对选项中的命题,判断正误即可.
【解答】
解:如图所示,
点O是正方形ABCD的中心,
根据正方形的特征,结合相等向量、平行向量的定义可知,①②③正确,
AO与BO只是模相等,由于方向不相同,所以不是相等向量,④是错误的.
7.【答案】B
【解析】
【分析】
本题主要考查向量的基本概念,以及向量与集合的综合.属于基础题.
由向量的基本概念以及集合间的基本关系可求得.
【解答】
解:∵A={与a→共线的向量},B={与a→长度相等的向量},C={与a→长度相等,方向相反的向量},其中a→是非零向量,
A.C?A,正确;
B.A∩B?{a→},所以不正确;
C.C?B,正确;
D.A∩B?{a→},正确;
故选B.
8.【答案】D
【解析】
【分析】
本题主要考查了向量相等的概念,是一个基础题.
根据相等向量的定义:大小相等,方向相同的向量为相等向量,逐项进行分析,即可得到答案.
【解答】
解:根据相等向量的定义,
A中,AD与BC的方向不同,故A错误;
B中,AC与BD的方向不同,故B错误;
C中,PE与PF的方向相反,故C错误;
D中,EP与PF的方向相同,且长度都等于线段EF长度的一半,故D正确.
故选D.
9.【答案】B
【解析】
【分析】
本题主要考查共线向量的定义,属于基础题.
由共线向量定义可直接判断.
【解答】
解:根据共线向量定义,可知AB,BC,AC这三个向量一定为共线向量,
故选B.
10.【答案】B
【解析】
【分析】
本题考查平面向量模的计算及平面向量几何表示,属基础题目.
结合图形可求向量的模长及平面向量几何表示,
【解答】
解:由题意AB=32+42=5,
因为D,E分别是△ABC的边AB,AC的中点,
所以?BC=2DE,
故选B.
11.【答案】③
【解析】
【分析】本题考查向量相等定义、向量共线定义,属于基础题.
根据向量相等定义可得故①错,②错,③正确,向量共线,只要满足方向相同或相反,a≠b,a与b可能共线.
【解答】解:起点和终点都相同的向量一定相等,但相等的向量只要求长度相等、方向相同,并不要求起点相同,故①错;
若AB=DC,则A,B,C,D四点还可能共线,②错;
当四边形ABCD为平行四边形时,AB=DC,③正确;
当a=b时,a与b一定共线,但当a与b共线时,不一定有a=b,故a≠b时,a与b可能共线,④错.
故填③.
12.【答案】OC
DC,EB
OB,OC,DC,EB,AD
【解析】∵ O是正三角形ABC的中心,∴ OA= OB= OC,易知四边形AOCD和四边形AOBE均为菱形,∴与AD相等的向量为OC;与OA共线的向量为DC,EB;与OA的模相等的向量为OB,OC,DC,EB,AD.
13.【答案】3π4
【解析】
【分析】
本题主要考查向量的几何应用,相等向量与共线向量,圆的面积计算公式,属于中档题.由向量相等与模相等的意义,将向量关系转化出几何关系,易知四边形ABCD为菱形,其内切圆半径为12|BD|sin?60°,即可得其面积.
【解答】解:由BC=AD知四边形ABCD为平行四边形,
由|AB|=|BD|=|BC|知四边形ABCD为菱形,△ABD为等边三角形,
故∠ABC=120°,菱形的内切圆圆心O在对角线BD、AC的交点处,
令其半径为r,则r=12|BD|sin?60°=32,
所以S圆=πr2=π×322=3π4.
故答案为3π4.
14.【答案】532
【解析】
【分析】本题考查了等边三角形的性质以及向量的模,属于基础题.
由题意可得,当D为BC的中点时,此时向量AD长度最小,问题得以解决.
【解答】根据题意,在等边△ABC中,有向线段AD长度最小时,AD应与边BC垂直,有向线段AD长度的最小值为等边△ABC的高,为532.
故答案为532.
15.【答案】解:(1)与DA平行的向量有AD,BC,CB;
(2)与DA的模相等的向量有:
AD,BC,CB,AB,BA,DC,CD,BD,DB.
【解析】本题考查向量平行的概念、向量的模,属于基础题.
(1)根据向量平行的概念直接求即可;
(2)根据向量模的概念求解..
16.【答案】解:(1)图形如下,
(2)图形如下,
C的终点是以A为圆心,5为半径的圆.
【解析】本题考查向量的几何表示.
(1)画出图形即可;
(2)画出图形,并指出终点的轨迹即可.
17.【答案】证明∵AB=DC,∴|AB|=|CD|且AB//CD,
∴四边形ABCD是平行四边形,∴|DA|=|CB|,且DA//CB.
又∵DA与CB的方向相同,∴CB=DA.
同理可证,四边形CNAM是平行四边形,
∴CM=NA.∵|CB|=|DA|,|CM|=|NA|,
∴|DN|=|MB|.
∵DN//MB且DN与MB的方向相同,∴DN=MB.
【解析】本题考查了相等向量与共线向量.属于基础题.
先证得四边形ABCD、四边形CNAM是平行四边形,由相等向量与共线向量定义证得DN=MB.
18.【答案】解:(1)向量AD,DC,CB,AB,如图所示:
(2)由题意知AD=BC,
所以ADBC,则四边形ABCD为平行四边形,
所以AB=DC,
则B地相对于A地的位移为“在北偏东60°的方向距A地6千米”.
【解析】本题考查向量的概念及几何表示、向量相等的概念,属于基础题.
(1)根据题意直接画即可;
(2)由题意知AD=BC.所以ADBC,则四边形ABCD为平行四边形,得出AB=DC,即可求出结果.
6.1 平面向量的概念 同步练习
班级 姓名 学号
一.选择题
下列说法中错误的是(????)
A. 零向量与任一向量平行
B. 方向相反的两个非零向量不一定共线
C. 零向量的长度为0
D. 方向相反的两个非零向量必不相等
设a,b为非零向量,则“a//b”是“a,b的方向相同”的? (??? )
A. 充分不必要条件 B. 必要不充分条件
C. 充分必要条件 D. 既不充分也不必要条件
如图,设O是正六边形ABCDEF的中心,则与BC相等的向量为? (??? )
A. BA
B. CD
C. AD
D. OD
给出下列命题:①零向量的长度为零,方向是任意的;②若a,b都是单位向量,则a=b;③向量AB与BA相等.则所有正确命题的序号是(????)
A. ① B. ③ C. ①③ D. ①②
已知向量a,b是两个非零向量,AO,BC分别是与a,b同方向的模为1的向量,则下列各式一定正确的是? (??? )
A. AO=BO B. AO=BO或AO=?BO
C. AO=1 D. |AO|=|BO|
如图所示,设O是正方形ABCD的中心,则下列结论正确的有____.(填序号)
? ①AO=OC; ②AO//AC; ③AB与CD共线; ④AO=BO.
已知集合A={与a共线的向量},B={与a长度相等的向量},C={与a长度相等、方向相反的向量},其中a为非零向量,则下列结论中错误的是? (??? )
A. C?A B. A?B={a} C. C?B D. A∩B?{a}
如图,在等腰梯形ABCD中,对角线AC与BD交于点P,点E,F分别在两腰AD,BC上,EF过点P,且EF//AB,则下列等式中成立的是(? ? ? ?)
A. AD=BC
B. AC=BD
C. PE=PF
D. EP=PF
已知向量AB与向量BC共线,下列关于向量AC的说法中,正确的是? (??? )
A. 向量AC与向量AB一定同向 B. 向量BC,AB,AC一定共线
C. 向量AC与向量BC一定相等 D. 以上说法都不正确
如图,网格纸上小正方形的边长为1,D,E分别是△ABC的边AB,AC的中点,则(? ? ?)
A. |AB|=5且|BC|=2.5|DE|
B. |AB|=5且|BC|=2|DE|
C. |AB|=6且|BC|=2|DE|
D. |AB|=6且|BC|=3|DE|
二.填空题
给出下列说法:
①两个向量,当且仅当它们的起点相同、终点相同时才相等;
②若AB=DC,则A,B,C,D为平行四边形的四个顶点;
③若四边形ABCD为平行四边形,则AB=DC;
④若a≠b,则a与b一定不共线.
其中正确说法的序号是____.
如图,O是正三角形ABC的中心,四边形AOCD和AOBE均为平行四边形,则与向量AD相等的向量为??????????;与向量OA共线的向量为??????????_;与向量OA的模相等的向量为??????????.(填图中所画出的向量)
已知在四边形ABCD中,BC=AD且|AB|=|BD|=|BC|=2,则四边形ABCD的内切圆的面积是_______.
若在一个边长为5的正三角形ABC中,一个向量所对应的有向线段为AD(其中D在边BC上运动),则向量AD的模的最小值为________.
三.解答题
如图,在菱形ABCD中,对角线AC,BD相交于O点,∠DAB=60°,分别以A,B,C,D,O中的不同两点作为向量的起点与终点.
(1)写出与DA平行的向量;
(2)写出与DA的模相等的向量.
如图,网格纸上小正方形的边长为1,已知向量a.
(1)试以B为终点画一个向量b,使b=a.
(2)在图中画一个以A为起点的向量c,使得|c|=5,并说出向量c的终点的轨迹是什么?
如图,已知四边形ABCD中,M,N分别是BC,AD上的点,AB=DC且CN=MA,求证:DN=MB.
一辆消防车从A地去B地执行任务,先从A地向北偏东30°方向行驶2千米到达D地,然后从D地沿北偏东60°方向行驶6千米到达C地,从C地又向南偏西30°方向行驶2千米才到达B地.
(1)在图中画出AD,DC,CB,AB;
(2)求B地相对于A地的位移.
答案和解析
1.【答案】B
【解析】
【分析】
本题考查了平面向量的基本概念,是基础题.
根据平面向量的基本概念,分析正误即可.
【解答】
解:对于A,零向量的方向是任意的,
零向量与任一向量平行,A正确;
对于B,方向相反的两个非零向量一定共线,B错误;
对于C,零向量的模长为0,C正确;
对于D,根据向量相等的定义知,方向相反的两个非零向量一定不相等,D正确.
故选:B.
2.【答案】B
【解析】
【分析】
本题考查充分条件、必要条件的判定方法,考查向量共线的概念,属于基础题.
由充分条件、必要条件的判定方法及向量共线的概念分析得答案.
【解答】
解:对于非零向量a,b,由a//b可得:a与b方向相同或相反,
反之,a与b方向相同?a//b,
则“a//b”是“a与b方向相同”的必要不充分条件.
故选B.
3.【答案】D
【解析】
【分析】
本题主要考查向量相等的定义,属于基础题.
由向量相等的定义,模相等,方向相同即可求解.
【解答】
解:根据图形可知四边形BCDO是平行四边形,∴BC?//?OD,BC=OD,∴BC=OD,
故选D.
4.【答案】A
【解析】
【分析】
本题主要考查向量的基本概念,属于基础题.
根据零向量、单位向量、相等向量的概念可一一判断.
【解答】
解:根据零向量的定义可知①正确;
根据单位向量的定义可知,单位向量的模相等,但方向不一定相同,故两个单位向量不一定相等,故②错误;
向量AB与BA互为相反向量,故③错误.
故选A.
5.【答案】D
【解析】
【分析】
本题考查向量的有关概念,属基础题,
由a,b只是模相等,方向不一定相同,可判断.
【解答】
解:由于a与b的方向不知,故AO与BO无法判断是否相等,故A、B选项均错.
又AO与BO均为单位向量,∴|AO|=|BO|,故C错,D对.
故选D.
6.【答案】①②③
【解析】
【分析】
本题考查了平面向量相等与共线定理的应用问题,是基础题.根据题意画出图形,结合图形对选项中的命题,判断正误即可.
【解答】
解:如图所示,
点O是正方形ABCD的中心,
根据正方形的特征,结合相等向量、平行向量的定义可知,①②③正确,
AO与BO只是模相等,由于方向不相同,所以不是相等向量,④是错误的.
7.【答案】B
【解析】
【分析】
本题主要考查向量的基本概念,以及向量与集合的综合.属于基础题.
由向量的基本概念以及集合间的基本关系可求得.
【解答】
解:∵A={与a→共线的向量},B={与a→长度相等的向量},C={与a→长度相等,方向相反的向量},其中a→是非零向量,
A.C?A,正确;
B.A∩B?{a→},所以不正确;
C.C?B,正确;
D.A∩B?{a→},正确;
故选B.
8.【答案】D
【解析】
【分析】
本题主要考查了向量相等的概念,是一个基础题.
根据相等向量的定义:大小相等,方向相同的向量为相等向量,逐项进行分析,即可得到答案.
【解答】
解:根据相等向量的定义,
A中,AD与BC的方向不同,故A错误;
B中,AC与BD的方向不同,故B错误;
C中,PE与PF的方向相反,故C错误;
D中,EP与PF的方向相同,且长度都等于线段EF长度的一半,故D正确.
故选D.
9.【答案】B
【解析】
【分析】
本题主要考查共线向量的定义,属于基础题.
由共线向量定义可直接判断.
【解答】
解:根据共线向量定义,可知AB,BC,AC这三个向量一定为共线向量,
故选B.
10.【答案】B
【解析】
【分析】
本题考查平面向量模的计算及平面向量几何表示,属基础题目.
结合图形可求向量的模长及平面向量几何表示,
【解答】
解:由题意AB=32+42=5,
因为D,E分别是△ABC的边AB,AC的中点,
所以?BC=2DE,
故选B.
11.【答案】③
【解析】
【分析】本题考查向量相等定义、向量共线定义,属于基础题.
根据向量相等定义可得故①错,②错,③正确,向量共线,只要满足方向相同或相反,a≠b,a与b可能共线.
【解答】解:起点和终点都相同的向量一定相等,但相等的向量只要求长度相等、方向相同,并不要求起点相同,故①错;
若AB=DC,则A,B,C,D四点还可能共线,②错;
当四边形ABCD为平行四边形时,AB=DC,③正确;
当a=b时,a与b一定共线,但当a与b共线时,不一定有a=b,故a≠b时,a与b可能共线,④错.
故填③.
12.【答案】OC
DC,EB
OB,OC,DC,EB,AD
【解析】∵ O是正三角形ABC的中心,∴ OA= OB= OC,易知四边形AOCD和四边形AOBE均为菱形,∴与AD相等的向量为OC;与OA共线的向量为DC,EB;与OA的模相等的向量为OB,OC,DC,EB,AD.
13.【答案】3π4
【解析】
【分析】
本题主要考查向量的几何应用,相等向量与共线向量,圆的面积计算公式,属于中档题.由向量相等与模相等的意义,将向量关系转化出几何关系,易知四边形ABCD为菱形,其内切圆半径为12|BD|sin?60°,即可得其面积.
【解答】解:由BC=AD知四边形ABCD为平行四边形,
由|AB|=|BD|=|BC|知四边形ABCD为菱形,△ABD为等边三角形,
故∠ABC=120°,菱形的内切圆圆心O在对角线BD、AC的交点处,
令其半径为r,则r=12|BD|sin?60°=32,
所以S圆=πr2=π×322=3π4.
故答案为3π4.
14.【答案】532
【解析】
【分析】本题考查了等边三角形的性质以及向量的模,属于基础题.
由题意可得,当D为BC的中点时,此时向量AD长度最小,问题得以解决.
【解答】根据题意,在等边△ABC中,有向线段AD长度最小时,AD应与边BC垂直,有向线段AD长度的最小值为等边△ABC的高,为532.
故答案为532.
15.【答案】解:(1)与DA平行的向量有AD,BC,CB;
(2)与DA的模相等的向量有:
AD,BC,CB,AB,BA,DC,CD,BD,DB.
【解析】本题考查向量平行的概念、向量的模,属于基础题.
(1)根据向量平行的概念直接求即可;
(2)根据向量模的概念求解..
16.【答案】解:(1)图形如下,
(2)图形如下,
C的终点是以A为圆心,5为半径的圆.
【解析】本题考查向量的几何表示.
(1)画出图形即可;
(2)画出图形,并指出终点的轨迹即可.
17.【答案】证明∵AB=DC,∴|AB|=|CD|且AB//CD,
∴四边形ABCD是平行四边形,∴|DA|=|CB|,且DA//CB.
又∵DA与CB的方向相同,∴CB=DA.
同理可证,四边形CNAM是平行四边形,
∴CM=NA.∵|CB|=|DA|,|CM|=|NA|,
∴|DN|=|MB|.
∵DN//MB且DN与MB的方向相同,∴DN=MB.
【解析】本题考查了相等向量与共线向量.属于基础题.
先证得四边形ABCD、四边形CNAM是平行四边形,由相等向量与共线向量定义证得DN=MB.
18.【答案】解:(1)向量AD,DC,CB,AB,如图所示:
(2)由题意知AD=BC,
所以ADBC,则四边形ABCD为平行四边形,
所以AB=DC,
则B地相对于A地的位移为“在北偏东60°的方向距A地6千米”.
【解析】本题考查向量的概念及几何表示、向量相等的概念,属于基础题.
(1)根据题意直接画即可;
(2)由题意知AD=BC.所以ADBC,则四边形ABCD为平行四边形,得出AB=DC,即可求出结果.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
