5.4 平抛运动的规律 课件—2020-2021学年【新教材】人教版(2019)高中物理必修第二册(18张PPT)
文档属性
| 名称 | 5.4 平抛运动的规律 课件—2020-2021学年【新教材】人教版(2019)高中物理必修第二册(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 576.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-25 19:43:59 | ||
图片预览



文档简介
第4节 抛体运动的规律
平抛运动的特点
水平:匀速直线运动
竖直:自由落体运动
复习
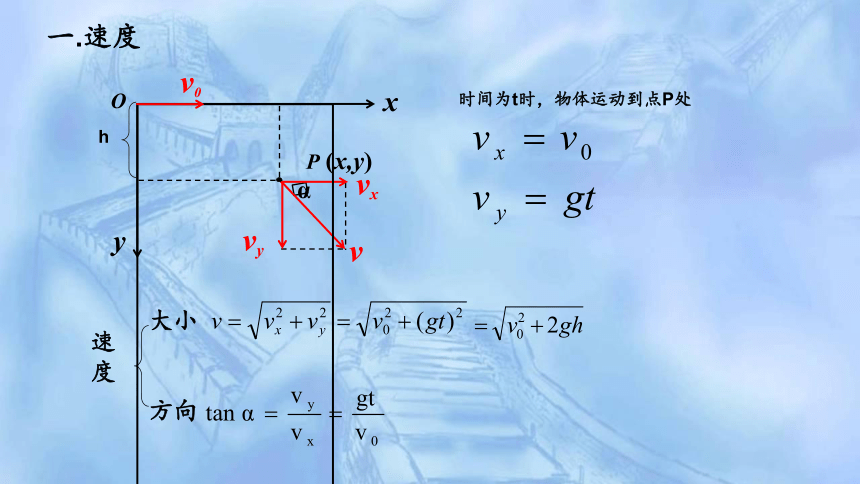
一.速度
α
vx
vy
v
O
x
y
v0
P (x,y)
速
度
大小
方向
时间为t时,物体运动到点P处
h
二.位移
l
O
x
y
P (x,y)
B
A
v0
位移
大小:
方向:
经过时间t,物体运动到点P处
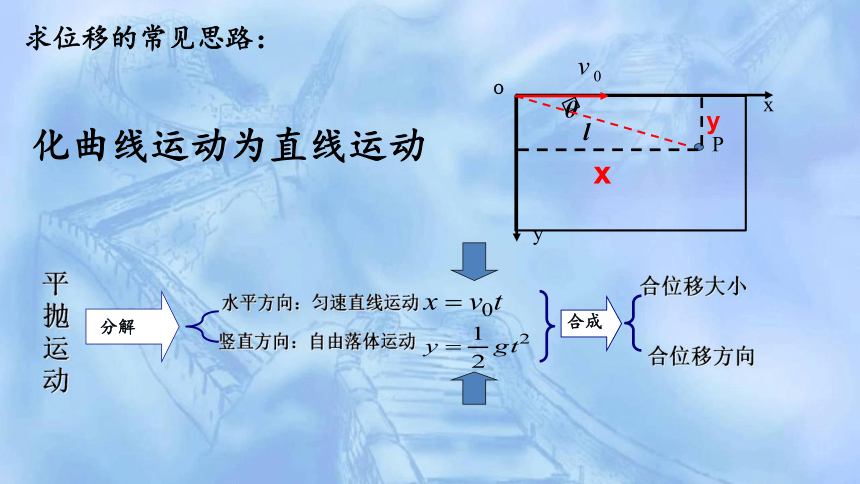
求位移的常见思路:
化曲线运动为直线运动
y
x
P
θ
l
o
x
y
竖直方向:自由落体运动
水平方向:匀速直线运动
合位移方向
合位移大小
平抛运动
分解
合成
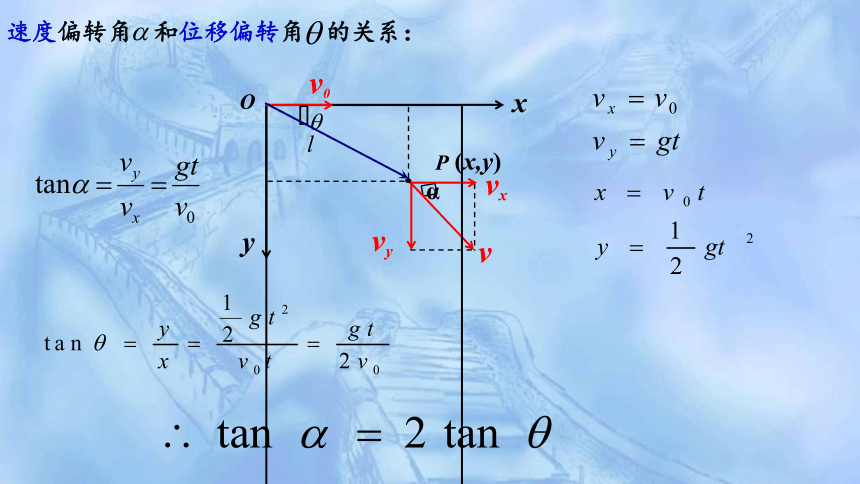
速度偏转角 和位移偏转角 的关系:
α
vx
vy
v
O
x
y
v0
P (x,y)
决定因素
(1)飞行时间:
(2)水平射程:
(3)落地速度:
x
o
y
例1.(临界极值)刀削面是北方人喜欢的面食之一,因其风味独特,驰名中外,刀削面全凭刀削,因此得名。如图所示,将一锅水烧开,拿一块面团放在锅旁边较高处,用一刀片飞快地削下一片片很薄的面片儿,面片便水平飞向锅里,若面团到锅的上沿的竖直距离为0.8m,最近的水平距离为 ,锅的半径为 ,要想使削出的面片落入锅中,则面片的水平速度可能是下列选项中的哪些?( )
A. 1.5m/s B.3m/s C.3.7m/s D.4m/s
面片在空中做平抛运动,竖直方向做自由落体运动,则有
所以面片落入锅中所用时间为
因为面片做平抛运动的水平位移满足
根据水平做匀速直线运动得
面片的水平初速度的范围为
故选ABC。
例2.(平抛和曲面结合问题)如图所示,半径为R的四分之一竖直圆弧轨道 ,O为圆心,C为圆弧轨道的中点。圆心O正左方的小球,以某初速度沿半径 方向水平拋出,已知拋出点到圆心O的距离等于R,重力加速度为g,则下列说法中正确的是( )
A.若小球以最小位移到达圆弧轨道,则初速度
B.若小球击中圆弧轨道上的A点,则飞行时间
C.若小球击中圆弧轨道上的C点,则飞行时间
D.若小球击中圆弧轨道上的C点,小球的速度方向不可能垂直于该点的切线
AB选项.若小球以最小位移到达圆弧轨道,即到达A点,则
解初速度
飞行时间
C.若小球击中圆弧轨道上的C点,则
选项A错误,B正确;
选项C错误;
D.根据平抛运动的推论,速度的反向延长线应该经过水平位移的中点;若小球击中圆弧轨道上的C点,小球的速度方向垂直于该点的切线,则速度的反向延长线经过圆心O,不是水平位移的中点,所以小球的速度方向不可能垂直于该点的切线,选项D正确。
故选BD。
练习一、如图所示,bc为竖直放置的半径为R的 圆弧,b点为圆弧最低点将小球从圆心处以大小不同的初速度v0水平抛出,球落到圆弧上。空气阻力可忽略,重力加速度大小为g,下列说法正确的是( )
A.落在圆弧上时的最小速度为
B.落在圆弧上时的最小速度为
C.小球的运动时间与v0大小无关
D.无论调整v0大小为何值,球都不可能垂直撞击在圆弧上
小球做平抛运动
而落点的速度
时速度取得最小值,代入可得最小值为
B正确,A错误;
C.v0越大,水平位移越大,竖直下落距离越小,运动时间越短,C错误;
D.由于速度的反向延长线恰好过与抛出点等高的水平位移的中点处,若与圆弧垂直,恰好与半径一致,两者相矛盾,因此球都不可能垂直撞击在圆弧上,D正确。
故选BD。
练习二、如图所示,两个小球从水平地面上方同一点O分别以初速度v1、v2水平抛出,落在地面上的位置分别是A、B,O′是O在地面上的竖直投影,且O′A∶AB=1∶3。若不计空气阻力,则两小球( )
A.落地速度大小之比为1∶3
B.抛出的初速度大小之比为1∶4
C.通过的位移大小之比为1∶
D.落地速度与水平地面夹角的正切值之比为4∶1
B.高度相同,所以下落时间相同,在水平方向上,有
因为水平位移之比为1∶4,所以抛出的初速度大小之比为1∶4,B正确;
A.小球落地速度大小为
故选BD。
练习三、如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点。圆上有一点D,且∠COD=60°。现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点。重力加速度为g,不计空气阻力。下列说法中正确的是( )
A.圆的半径为R=
B.圆的半径为R=
C.甲小球不能垂直击中C点
D.乙小球能垂直击中D点
甲球击中C点,根据
解得:
故B正确,A错误;
C.甲球速度方向若垂直击中C点,则速度方向变为竖直向下,平抛运动的速度方向不可能竖直向下,故C正确。
D.若乙小球的速度方向垂直击中D点,则速度的反向延长线经过圆心,根据几何关系知,速度与水平方向的夹角是位移与水平方向夹角的2倍,与速度与水平方向夹角的正切值是位移与水平方向夹角的正切值的2倍相矛盾,故D错误。
故选BC。
v0
v0
o
vy
x
y
v
)
)
α
θ
s
X
Y
小结
平抛运动的特点
水平:匀速直线运动
竖直:自由落体运动
复习
一.速度
α
vx
vy
v
O
x
y
v0
P (x,y)
速
度
大小
方向
时间为t时,物体运动到点P处
h
二.位移
l
O
x
y
P (x,y)
B
A
v0
位移
大小:
方向:
经过时间t,物体运动到点P处
求位移的常见思路:
化曲线运动为直线运动
y
x
P
θ
l
o
x
y
竖直方向:自由落体运动
水平方向:匀速直线运动
合位移方向
合位移大小
平抛运动
分解
合成
速度偏转角 和位移偏转角 的关系:
α
vx
vy
v
O
x
y
v0
P (x,y)
决定因素
(1)飞行时间:
(2)水平射程:
(3)落地速度:
x
o
y
例1.(临界极值)刀削面是北方人喜欢的面食之一,因其风味独特,驰名中外,刀削面全凭刀削,因此得名。如图所示,将一锅水烧开,拿一块面团放在锅旁边较高处,用一刀片飞快地削下一片片很薄的面片儿,面片便水平飞向锅里,若面团到锅的上沿的竖直距离为0.8m,最近的水平距离为 ,锅的半径为 ,要想使削出的面片落入锅中,则面片的水平速度可能是下列选项中的哪些?( )
A. 1.5m/s B.3m/s C.3.7m/s D.4m/s
面片在空中做平抛运动,竖直方向做自由落体运动,则有
所以面片落入锅中所用时间为
因为面片做平抛运动的水平位移满足
根据水平做匀速直线运动得
面片的水平初速度的范围为
故选ABC。
例2.(平抛和曲面结合问题)如图所示,半径为R的四分之一竖直圆弧轨道 ,O为圆心,C为圆弧轨道的中点。圆心O正左方的小球,以某初速度沿半径 方向水平拋出,已知拋出点到圆心O的距离等于R,重力加速度为g,则下列说法中正确的是( )
A.若小球以最小位移到达圆弧轨道,则初速度
B.若小球击中圆弧轨道上的A点,则飞行时间
C.若小球击中圆弧轨道上的C点,则飞行时间
D.若小球击中圆弧轨道上的C点,小球的速度方向不可能垂直于该点的切线
AB选项.若小球以最小位移到达圆弧轨道,即到达A点,则
解初速度
飞行时间
C.若小球击中圆弧轨道上的C点,则
选项A错误,B正确;
选项C错误;
D.根据平抛运动的推论,速度的反向延长线应该经过水平位移的中点;若小球击中圆弧轨道上的C点,小球的速度方向垂直于该点的切线,则速度的反向延长线经过圆心O,不是水平位移的中点,所以小球的速度方向不可能垂直于该点的切线,选项D正确。
故选BD。
练习一、如图所示,bc为竖直放置的半径为R的 圆弧,b点为圆弧最低点将小球从圆心处以大小不同的初速度v0水平抛出,球落到圆弧上。空气阻力可忽略,重力加速度大小为g,下列说法正确的是( )
A.落在圆弧上时的最小速度为
B.落在圆弧上时的最小速度为
C.小球的运动时间与v0大小无关
D.无论调整v0大小为何值,球都不可能垂直撞击在圆弧上
小球做平抛运动
而落点的速度
时速度取得最小值,代入可得最小值为
B正确,A错误;
C.v0越大,水平位移越大,竖直下落距离越小,运动时间越短,C错误;
D.由于速度的反向延长线恰好过与抛出点等高的水平位移的中点处,若与圆弧垂直,恰好与半径一致,两者相矛盾,因此球都不可能垂直撞击在圆弧上,D正确。
故选BD。
练习二、如图所示,两个小球从水平地面上方同一点O分别以初速度v1、v2水平抛出,落在地面上的位置分别是A、B,O′是O在地面上的竖直投影,且O′A∶AB=1∶3。若不计空气阻力,则两小球( )
A.落地速度大小之比为1∶3
B.抛出的初速度大小之比为1∶4
C.通过的位移大小之比为1∶
D.落地速度与水平地面夹角的正切值之比为4∶1
B.高度相同,所以下落时间相同,在水平方向上,有
因为水平位移之比为1∶4,所以抛出的初速度大小之比为1∶4,B正确;
A.小球落地速度大小为
故选BD。
练习三、如图所示,在竖直平面内有一个以AB为水平直径的半圆,O为圆心,C为最低点。圆上有一点D,且∠COD=60°。现在A点分别以速率v1、v2沿AB方向先后抛出甲、乙两小球,甲球击中C点,乙球击中D点。重力加速度为g,不计空气阻力。下列说法中正确的是( )
A.圆的半径为R=
B.圆的半径为R=
C.甲小球不能垂直击中C点
D.乙小球能垂直击中D点
甲球击中C点,根据
解得:
故B正确,A错误;
C.甲球速度方向若垂直击中C点,则速度方向变为竖直向下,平抛运动的速度方向不可能竖直向下,故C正确。
D.若乙小球的速度方向垂直击中D点,则速度的反向延长线经过圆心,根据几何关系知,速度与水平方向的夹角是位移与水平方向夹角的2倍,与速度与水平方向夹角的正切值是位移与水平方向夹角的正切值的2倍相矛盾,故D错误。
故选BC。
v0
v0
o
vy
x
y
v
)
)
α
θ
s
X
Y
小结
