北师大版2021年八年级下册第五章《分式与分式方程》章末题型分类训练卷(Word版含解析)
文档属性
| 名称 | 北师大版2021年八年级下册第五章《分式与分式方程》章末题型分类训练卷(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 241.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 00:00:00 | ||
图片预览




文档简介
北师大版2021年八年级下册第五章《分式与分式方程》章末题型分类训练卷
一.分式方程的定义
1.下列方程是分式方程的是( )
A. B. C.x2﹣1=0 D.2x+1=3x
2.下列方程中,是分式方程的是( )
A.+=1 B.x+=2 C.2x=x﹣5 D.x﹣4y=1
3.下列关于x的方程是分式方程的为( )
A.﹣x= B.=1﹣
C.+1= D.=
4.下列关于x的方程中,是分式方程的是( )
A.﹣3= B.﹣﹣
C.=3﹣x D.=1
5.下列关于x的方程①,②,③,④中,是分式方程的有( )
A.4个 B.3个 C.2个 D.1个
二.分式的方程的解
6.已知关于x的方程的解是正数,则m的取值范围为 .
7.若关于x的方程=1的解是负数,则a的取值范围是 .
8.若关于x的方程=+1无解,则a的值为( )
A.1 B.2 C.1或2 D.0或2
9.已知关于x的分式方程+﹣1=0有整数解,且关于x的不等式组有且只有3个整数解,则符合条件的所有整数a的个数为( )
A.1 B.2 C.3 D.4
10.若关于x的不等式组有解,且关于x的分式方程的解为非负数,则满足条件的整数a的值的和为( )
A.﹣10 B.﹣7 C.﹣9 D.﹣8
三.解分式方程、换元法
11.解分式方程,分以下四步,其中,错误的一步是( )
A.方程两边分式的最简公分母是(x﹣1)(x+1)
B.方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1
12.解分式方程:﹣=.
13.解分式方程:﹣=1.
14.解分式方程:﹣1=.
15.解分式方程:.
16.用换元法解分式方程x2﹣x+=1时,如果设x2﹣x=y,则原方程可化为关于y的整式方程是( )
A.y2+2y+1=0 B.y2+2y﹣1=0 C.y2﹣y+2=0 D.y2+y﹣2=0
17.用换元法解分式方程时,如果设,那么原方程可化为( )
A.2y2+3y﹣5=0 B.2y2﹣5y+3=0 C.y2+3y﹣5=0 D.y2﹣5y+3=0
18.已知实数x满足x2++x﹣=4,则x﹣的值是( )
A.﹣2 B.1 C.﹣1或2 D.﹣2或1
19.已知方程,如果设,那么原方程可以变形为 .
20.在方程=3x﹣4中,如果设y=x2﹣3x,那么原方程可化为关于y的整式方程是 .
四.分式方程的增根
21.若关于x的方程有增根,则k的值为( )
A.3 B.1 C.0 D.﹣1
22.若关于x的分式方程+=1有增根,则m的值是( )
A.m=0 B.m=﹣1 C.m=0或m=3 D.m=3
23.若关于x的方程=有增根,则m的值与增根x的值分别是( )
A.m=﹣4,x=2 B.m=4,x=2 C.m=﹣4,x=﹣2 D.m=4,x=﹣2
24.关于x的方程:﹣=1.
(1)当a=3时,求这个方程的解;
(2)若这个方程有增根,求a的值.
25.m为何值时,关于x的方程 +=会产生增根?
五.由实际问题抽象出分式方程
26.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A. B.
C. D.
27.《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B.
C. D.
28.某部门组织调运一批物资,一运送物资车开往距离出发地180千米的目的地,出发第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地.设原计划速度为x千米/小时,则方程可列为( )
A.=
B.=
C.+1=﹣
D.+1=+
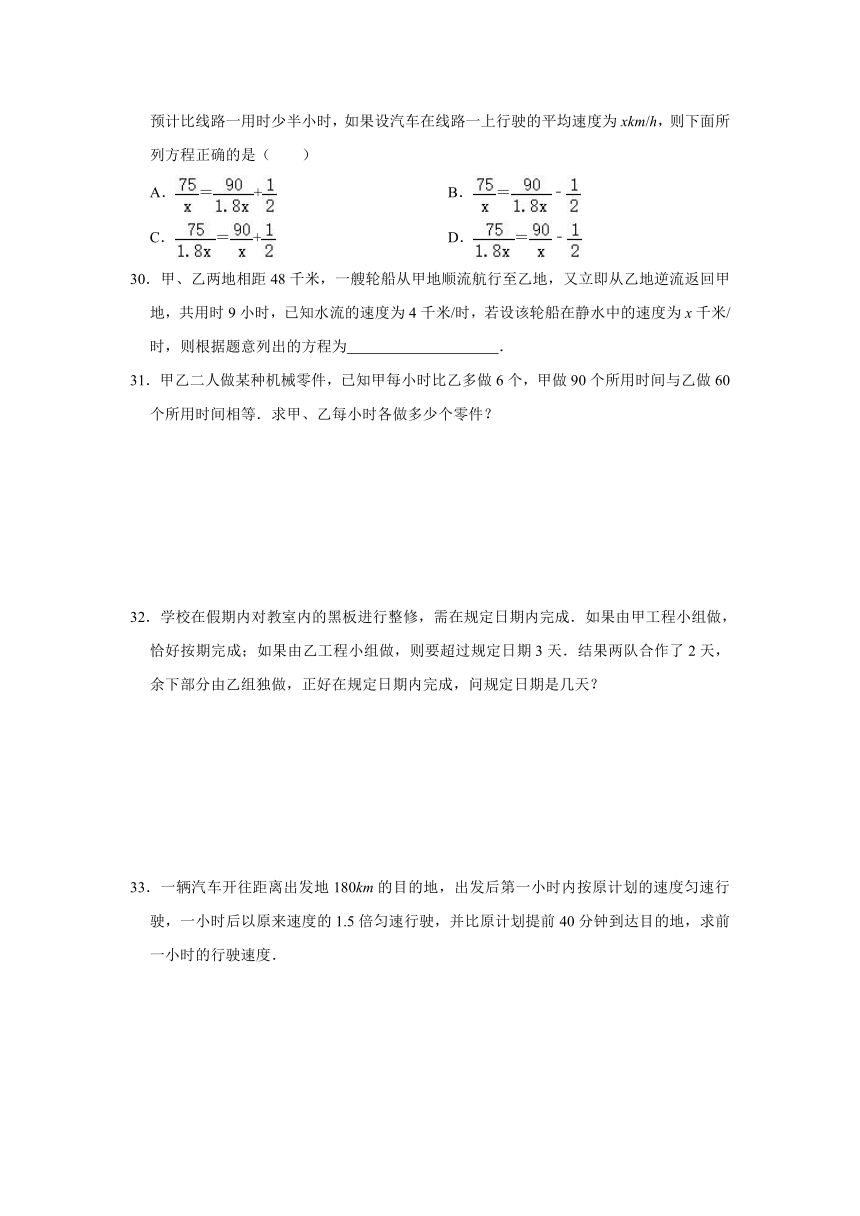
29.小东一家自驾车去某地旅行,手机导航系统推荐了两条线路,线路一全程75km,线路二全程90km,汽车在线路二上行驶的平均时速是线路一上车速的1.8倍,线路二的用时预计比线路一用时少半小时,如果设汽车在线路一上行驶的平均速度为xkm/h,则下面所列方程正确的是( )
A.=+ B.=﹣
C.=+ D.=﹣
30.甲、乙两地相距48千米,一艘轮船从甲地顺流航行至乙地,又立即从乙地逆流返回甲地,共用时9小时,已知水流的速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则根据题意列出的方程为 .
31.甲乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等.求甲、乙每小时各做多少个零件?
32.学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?
33.一辆汽车开往距离出发地180km的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地,求前一小时的行驶速度.
34.在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.
(1)求甲、乙两条生产线每天的产能各是多少?
(2)若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?
(3)正式开工满负荷生产3天后,通过技术革新,甲生产线的日产能提高了50%,乙生产线的日产能翻了一番.再满负荷生产13天能否完成任务?
35.倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
36.某小区为了排污,需铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,需缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前2天完成任务.求原计划每天铺设多少米?
37.某服装店用960元购进一批服装,并以每件46元的价格全部售完,由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售,卖了部分后,为了加快资金周转,服装店将剩余的20件以售价的九折全部出售.问:
(1)该服装店第一次购买了此种服装多少件?
(2)两次出售服装共盈利多少元?
38.某中学为了创设“书香校园”,准备购买A,B两种书架,用于放置图书.在购买时发现,A种书架的单价比B种书架的单价多20元,用600元购买A种书架的个数与用480元购买B种书架的个数相同.
(1)求A,B两种书架的单价各是多少元?
(2)学校准备购买A,B两种书架共15个,且购买的总费用不超过1400元,求最多可以购买多少个A种书架?
39.某社区拟建A,B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米.建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元.用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的.
(1)求每个A,B类摊位占地面积各为多少平方米?
(2)该社区拟建A,B两类摊位共90个,且B类摊位的数量不少于A类摊位数量的3倍.求建造这90个摊位的最大费用.
40.“阅读陪伴成长,书香润泽人生.”某校为了开展学生阅读活动,计划从书店购进若干本A、B两类图书(每本A类图书的价格相同,每本B类图书的价格也相同),且每本A类图书的价格比每本B类图书的价格多5元,用1200元购进的A类图书与用900元购进的B类图书册数相同.
(1)求每本A类图书和每本B类图书的价格各为多少元?
(2)根据学校实际情况,需从书店一次性购买A、B两类图书共300册,购买时得知:一次性购买A、B两类图书超过100册时,A类图书九折优惠(B类图书按原价销售),若该校此次用于购买A、B两类图书的总费用不超过5100元,那么最多可以购买多少本A类图书?
参考答案
一.分式方程的定义
1.解:A、该方程属于一元一次方程,不符合题意.
B、该方程属于分式方程,符合题意.
C、该方程属于一元二次方程,不符合题意.
D、该方程属于一元一次方程,不符合题意.
故选:B.
2.解:A、该方程是一元一次方程,故本选项不符合题意;
B、该方程符合分式方程的定义,故本选项符合题意;
C、该方程是一元一次方程,故本选项不符合题意;
D、该方程是二元一次方程,故本选项不符合题意;
故选:B.
3.解:A、方程分母中不含未知数,故不是分式方程;
B、方程分母中含未知数x,故是分式方程;
C、方程分母中不含表示未知数的字母,π是常数;
D、方程分母中不含未知数,故不是分式方程.
故选:B.
4.解:A、C选项项中的方程分母中不含未知数,故不是分式方程;
B选项不是方程.
D选项中的方程分母中含未知数x,故是分式方程,
故选:D.
5.解:关于x的方程②,③中,分母中都含有字母,都是分式方程;
关于x的方程①,④中,分母中不含未知数,故不是分式方程.
综上所述,是分式方程的有②、③,共2个.
故选:C.
二.分式的方程的解
6.解:分式方程去分母得:2x﹣m=x﹣1,
解得:x=m﹣1,
由分式方程的解为正数,得到m﹣1>0,且m﹣1≠1,
解得:m>1且m≠2,
故答案为:m>1且m≠2.
7.解:去分母得:2x+a=x+1,
解得:x=1﹣a,
由解为负数,得到1﹣a<0,且1﹣a≠﹣1,
解得:a>1且a≠2,
故答案为:a>1且a≠2
8.解:方程去分母得:ax=4+x﹣2
解得:(a﹣1)x=2,
∴当a﹣1=0即a=1时,整式方程无解,分式方程无解;
当a≠1时,x=
x=2时分母为0,方程无解,
即=2,
∴a=2时方程无解.
故选:C.
9.解:分式方程去分母得:1﹣ax﹣3﹣2+x=0,即(1﹣a)x=4,
由分式方程有整数解,得到1﹣a≠0,
解得:x=,
不等式组整理得:,即﹣3≤x<,
由不等式组有且只有3个整数解,得到﹣1<≤0,
解得:﹣1<a≤,
由x为整数,且≠2,得到1﹣a=±1,﹣2,±4,
解得:a=0,
则符合条件的所有整数a的个数为1,
故选:A.
10.解:不等式组整理得:,
由不等式组有解,得到﹣5≤x<a,
解得:a>﹣5,
,
分式方程去分母得:ax﹣x+2=﹣3x,
解得:x=,
∵关于x的分式方程的解为非负数,
∴≥0,解得a≤1,
当a=﹣1时,x=1(不合题意舍去)
∴﹣5<a≤1,
∵a为整数,
∴a=﹣4,﹣3,﹣2,0,1,
则满足题意的整数a的值的和是﹣2﹣3﹣4+0+1=﹣8.
故选:D.
三.解分式方程、换元法
11.解:分式方程的最简公分母为(x﹣1)(x+1),
方程两边乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6,
解得:x=1,
经检验x=1是增根,分式方程无解.
故选:D.
12.解:去分母得:3﹣2(x+3)=x﹣3,
去括号得:3﹣2x﹣6=x﹣3,
移项合并得:﹣3x=0,
解得:x=0,
经检验x=0是分式方程的解.
13.解:﹣=1
(x+1)2﹣4=x2﹣1
x2+2x+1﹣4=x2﹣1
x=1,
检验:把x=1代入x2﹣1=1﹣1=0,
∴x=1不是原方程的根,原方程无解.
14.解:原方程变形为:﹣1=,
方程两边同乘以3(x+1),得3x﹣3x﹣3=2x,
解得:x=﹣1.5,
经检验,x=﹣1.5是原方程的根.
15.解:=方程的两边同乘(x﹣1)(x﹣3)得,
2(x﹣1)=x﹣3解得,
x=﹣1
检验:把x=﹣1代入(x﹣1)(x﹣3)≠0
∴原方程的解为:x=﹣1
16.解:设x2﹣x=y,原方程等价于y﹣1+=0,
两边都乘以y,得
y2﹣y+2=0,
故选:C.
17.解:设=y,则原方程化为2y2+3y﹣5=0.
故选:A.
18.解:x2+﹣2+x﹣﹣2=0
∴(x﹣)2+(x﹣)﹣2=0
解得x﹣=﹣2或1.
经检验,x﹣=1和x﹣=﹣2均有实数根.
所以x﹣=﹣2或1.
故选:D.
19.解:根据题意得:设,
则=,
∴原方程可变为;
故答案为.
20.解:根据等式的性质原方程可整理为x2﹣3x++4=0.
把y=x2﹣3x代入可得y++4=0,
去分母得y2+4y+3=0.
四.分式方程的增根
21.解:方程两边都乘x﹣1,
得:3=x﹣1+k,
∵原方程有增根,
∴最简公分母x﹣1=0,
解得x=1,
当x=1时,k=3.
故k的值为3.
故选:A.
22.解:方程两边都乘x﹣4,
得3﹣(x+m)=x﹣4,
∵原方程有增根,
∴最简公分母x﹣4=0,
解得x=4,
当x=4时,3﹣(4+m)=4﹣4,
m=﹣1,
故选:B.
23.解:去分母得:x+2=m,
由分式方程有增根,得到x﹣2=0,即x=2,
把x=2代入整式方程得:m=4,
则m的值与增根x的值分别是m=4,x=2,
故选:B.
24.解:(1)当a=3时,原方程为﹣=1,
方程两边同时乘以(x﹣1)得:3x+1+2=x﹣1,
解这个整式方程得:x=﹣2,
检验:将x=﹣2代入x﹣1=﹣2﹣1=﹣3≠0,
∴x=﹣2是原方程的解;
(2)方程两边同时乘以(x﹣1)得ax+1+2=x﹣1,即(a﹣1)x=﹣4,
当a≠1时,若原方程有增根,则x﹣1=0,
解得:x=1,
将x=1代入整式方程得:a+1+2=0,
解得:a=﹣3,
综上,a的值为﹣3.
25.解:原方程化为+=,
方程两边同时乘以(x+2)(x﹣2)
得2(x+2)+mx=3(x﹣2),
整理得(m﹣1)x+10=0,
∵关于x的方程 +=会产生增根,
∴(x+2)(x﹣2)=0,
∴x=﹣2 或x=2,
∴当x=﹣2时,(m﹣1)×(﹣2)+10=0,解得m=6,
当x=2时,(m﹣1)×2+10=0,解得m=﹣4,
∴m=﹣4或m=6时,原方程会产生增根.
五.由实际问题抽象出分式方程
26.解:若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
27.解:设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得:
×2=,
故选:A.
28.解:设原计划速度为x千米/小时,
根据题意得:
原计划的时间为:,
实际的时间为:+1,
∵实际比原计划提前40分钟到达目的地,
∴+1=﹣,
故选:C.
29.解:设汽车在线路一上行驶的平均速度为xkm/h,则在线路二上行驶的平均速度为1.8xkm/h,
由题意得:=+,
故选:A.
30.解:顺流所用的时间为:,逆流所用的时间为:.所列方程为:=9.
31.解:设乙每小时做x个零件,甲每小时做(x+6)个零件,
根据题意得:,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+6=18.
答:乙每小时做12个零件,甲每小时做18个零件.
32.解:设规定日期为x天,
根据题意,得2(+)+×(x﹣2)=1
解这个方程,得x=6
经检验,x=6
是原方程的解.
∴原方程的解是x=6.
答:规定日期是6天.
33.解:设前一小时的行驶速度为xkm/h,根据题意可得:
+1=﹣,
解得:x=60,
检验得:x=60是原方程的根,
答:前一小时的行驶速度为60km/h.
34.解:(1)设乙条生产线每天的产能是x万个,则甲条生产线每天的产能是2x万个,依题意有
﹣=2,
解得x=20,
经检验,x=20是原方程的解,
2x=2×20=40,
故甲条生产线每天的产能是40万个,乙条生产线每天的产能是20万个;
(2)设安排乙生产线生产y天,依题意有
0.5y+1.2×≤40,
解得y≥32.
故至少应安排乙生产线生产32天;
(3)(40+20)×3+[40×(1+50%)+20×2]×13
=180+1300
=1480(万个),
1440万个<1480万个,
故再满负荷生产13天能完成任务.
35.解:(1)设A种型号健身器材的单价为x元/套,B种型号健身器材的单价为1.5x元/套,
根据题意,可得:,
解得:x=360,
经检验x=360是原方程的根,
1.5×360=540(元),
因此,A,B两种健身器材的单价分别是360元,540元;
(2)设购买A种型号健身器材m套,则购买B种型号的健身器材(50﹣m)套,
根据题意,可得:360m+540(50﹣m)≤21000,
解得:m≥33,
因此,A种型号健身器材至少购买34套.
36.解:设原计划每天铺设管道x米,则实际每天铺设管道1.2x米,
由题意,得﹣=2.
解得:x=60.
经检验,x=60是原方程的解.且符合题意.
答:原计划每天铺设管道60米.
37.解:(1)设第一次购买了此种服装x件,那么第二次购进2x件,
依题意得,
解之得x=30,
经检验x=30是方程的解,
答:第一次购买了此种服装30件;
(2)∵第一次购买了此种服装30件,盈利46×30﹣960=420元;
∴第二次购买了此种服装60件,46×(60﹣20)+46×0.9×20﹣2220=448元;
∴两次出售服装共盈利420+448=868元.
38.解:(1)设B种书架的单价为x元,根据题意,得.
解得x=80.
经检验:x=80是原分式方程的解.
∴x+20=100.
答:购买A种书架需要100元,B种书架需要80元.
(2)设准备购买m个A种书架,根据题意,得100m+80(15﹣m)≤1400.
解得m≤10.
答:最多可购买10个A种书架.
39.解:(1)设每个B类摊位的占地面积为x平方米,则每个A类摊位占地面积为(x+2)平方米,
根据题意得:,
解得:x=3,
经检验x=3是原方程的解,
所以3+2=5,
答:每个A类摊位占地面积为5平方米,每个B类摊位的占地面积为3平方米;
(2)解法一:设建A摊位a个,建造这90个摊位的费用为y元,则建B摊位(90﹣a)个,
由题意得:y=5a×40+3×30(90﹣a)=110a+8100,
∵110>0,
∴y随a的增大而增大,
∵90﹣a≥3a,
解得a≤22.5,
∵a为整数,
∴当a取最大值22时,费用最大,
此时最大费用为:110×22+8100=10520;
解法二:设建A摊位a(a为整数)个,则建B摊位(90﹣a)个,
由题意得:90﹣a≥3a,
解得a≤22.5,
∵建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,
∴要想使建造这90个摊位有最大费用,所以要多建造A类摊位,即a取最大值22时,费用最大,
此时最大费用为:22×40×5+30×(90﹣22)×3=10520,
答:建造这90个摊位的最大费用是10520元.
40.解:(1)设每本A类图书的价格是x元,则每本B类图书的价格是(x﹣5)元,根据题意可得:
,
解得:x=20,
经检验x=20是方程的解,所以x﹣5=20﹣5=15,
答:每本A类图书的价格是20元,每本B类图书的价格是15元;
(2)设该校A类图书y本,则B类图书(300﹣y),
根据题意可得:20×90%y+15×(300﹣y)≤5100,
解得:y≤200,
答:最多可以购买200本A类图书.
一.分式方程的定义
1.下列方程是分式方程的是( )
A. B. C.x2﹣1=0 D.2x+1=3x
2.下列方程中,是分式方程的是( )
A.+=1 B.x+=2 C.2x=x﹣5 D.x﹣4y=1
3.下列关于x的方程是分式方程的为( )
A.﹣x= B.=1﹣
C.+1= D.=
4.下列关于x的方程中,是分式方程的是( )
A.﹣3= B.﹣﹣
C.=3﹣x D.=1
5.下列关于x的方程①,②,③,④中,是分式方程的有( )
A.4个 B.3个 C.2个 D.1个
二.分式的方程的解
6.已知关于x的方程的解是正数,则m的取值范围为 .
7.若关于x的方程=1的解是负数,则a的取值范围是 .
8.若关于x的方程=+1无解,则a的值为( )
A.1 B.2 C.1或2 D.0或2
9.已知关于x的分式方程+﹣1=0有整数解,且关于x的不等式组有且只有3个整数解,则符合条件的所有整数a的个数为( )
A.1 B.2 C.3 D.4
10.若关于x的不等式组有解,且关于x的分式方程的解为非负数,则满足条件的整数a的值的和为( )
A.﹣10 B.﹣7 C.﹣9 D.﹣8
三.解分式方程、换元法
11.解分式方程,分以下四步,其中,错误的一步是( )
A.方程两边分式的最简公分母是(x﹣1)(x+1)
B.方程两边都乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6
C.解这个整式方程,得x=1
D.原方程的解为x=1
12.解分式方程:﹣=.
13.解分式方程:﹣=1.
14.解分式方程:﹣1=.
15.解分式方程:.
16.用换元法解分式方程x2﹣x+=1时,如果设x2﹣x=y,则原方程可化为关于y的整式方程是( )
A.y2+2y+1=0 B.y2+2y﹣1=0 C.y2﹣y+2=0 D.y2+y﹣2=0
17.用换元法解分式方程时,如果设,那么原方程可化为( )
A.2y2+3y﹣5=0 B.2y2﹣5y+3=0 C.y2+3y﹣5=0 D.y2﹣5y+3=0
18.已知实数x满足x2++x﹣=4,则x﹣的值是( )
A.﹣2 B.1 C.﹣1或2 D.﹣2或1
19.已知方程,如果设,那么原方程可以变形为 .
20.在方程=3x﹣4中,如果设y=x2﹣3x,那么原方程可化为关于y的整式方程是 .
四.分式方程的增根
21.若关于x的方程有增根,则k的值为( )
A.3 B.1 C.0 D.﹣1
22.若关于x的分式方程+=1有增根,则m的值是( )
A.m=0 B.m=﹣1 C.m=0或m=3 D.m=3
23.若关于x的方程=有增根,则m的值与增根x的值分别是( )
A.m=﹣4,x=2 B.m=4,x=2 C.m=﹣4,x=﹣2 D.m=4,x=﹣2
24.关于x的方程:﹣=1.
(1)当a=3时,求这个方程的解;
(2)若这个方程有增根,求a的值.
25.m为何值时,关于x的方程 +=会产生增根?
五.由实际问题抽象出分式方程
26.暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A. B.
C. D.
27.《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B.
C. D.
28.某部门组织调运一批物资,一运送物资车开往距离出发地180千米的目的地,出发第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地.设原计划速度为x千米/小时,则方程可列为( )
A.=
B.=
C.+1=﹣
D.+1=+
29.小东一家自驾车去某地旅行,手机导航系统推荐了两条线路,线路一全程75km,线路二全程90km,汽车在线路二上行驶的平均时速是线路一上车速的1.8倍,线路二的用时预计比线路一用时少半小时,如果设汽车在线路一上行驶的平均速度为xkm/h,则下面所列方程正确的是( )
A.=+ B.=﹣
C.=+ D.=﹣
30.甲、乙两地相距48千米,一艘轮船从甲地顺流航行至乙地,又立即从乙地逆流返回甲地,共用时9小时,已知水流的速度为4千米/时,若设该轮船在静水中的速度为x千米/时,则根据题意列出的方程为 .
31.甲乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等.求甲、乙每小时各做多少个零件?
32.学校在假期内对教室内的黑板进行整修,需在规定日期内完成.如果由甲工程小组做,恰好按期完成;如果由乙工程小组做,则要超过规定日期3天.结果两队合作了2天,余下部分由乙组独做,正好在规定日期内完成,问规定日期是几天?
33.一辆汽车开往距离出发地180km的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地,求前一小时的行驶速度.
34.在抗击“新冠肺炎”战役中,某公司接到转产生产1440万个医用防护口罩补充防疫一线需要的任务,临时改造了甲、乙两条流水生产线.试产时甲生产线每天的产能(每天的生产的数量)是乙生产线的2倍,各生产80万个,甲比乙少用了2天.
(1)求甲、乙两条生产线每天的产能各是多少?
(2)若甲、乙两条生产线每天的运行成本分别是1.2万元和0.5万元,要使完成这批任务总运行成本不超过40万元,则至少应安排乙生产线生产多少天?
(3)正式开工满负荷生产3天后,通过技术革新,甲生产线的日产能提高了50%,乙生产线的日产能翻了一番.再满负荷生产13天能否完成任务?
35.倡导健康生活推进全民健身,某社区去年购进A,B两种健身器材若干件,经了解,B种健身器材的单价是A种健身器材的1.5倍,用7200元购买A种健身器材比用5400元购买B种健身器材多10件.
(1)A,B两种健身器材的单价分别是多少元?
(2)若今年两种健身器材的单价和去年保持不变,该社区计划再购进A,B两种健身器材共50件,且费用不超过21000元,请问:A种健身器材至少要购买多少件?
36.某小区为了排污,需铺设一段全长为720米的排污管道,为减少施工对居民生活的影响,需缩短施工时间,实际施工时每天的工作效率比原计划提高20%,结果提前2天完成任务.求原计划每天铺设多少米?
37.某服装店用960元购进一批服装,并以每件46元的价格全部售完,由于服装畅销,服装店又用2220元,再次以比第一次进价多5元的价格购进服装,数量是第一次购进服装的2倍,仍以每件46元的价格出售,卖了部分后,为了加快资金周转,服装店将剩余的20件以售价的九折全部出售.问:
(1)该服装店第一次购买了此种服装多少件?
(2)两次出售服装共盈利多少元?
38.某中学为了创设“书香校园”,准备购买A,B两种书架,用于放置图书.在购买时发现,A种书架的单价比B种书架的单价多20元,用600元购买A种书架的个数与用480元购买B种书架的个数相同.
(1)求A,B两种书架的单价各是多少元?
(2)学校准备购买A,B两种书架共15个,且购买的总费用不超过1400元,求最多可以购买多少个A种书架?
39.某社区拟建A,B两类摊位以搞活“地摊经济”,每个A类摊位的占地面积比每个B类摊位的占地面积多2平方米.建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元.用60平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的.
(1)求每个A,B类摊位占地面积各为多少平方米?
(2)该社区拟建A,B两类摊位共90个,且B类摊位的数量不少于A类摊位数量的3倍.求建造这90个摊位的最大费用.
40.“阅读陪伴成长,书香润泽人生.”某校为了开展学生阅读活动,计划从书店购进若干本A、B两类图书(每本A类图书的价格相同,每本B类图书的价格也相同),且每本A类图书的价格比每本B类图书的价格多5元,用1200元购进的A类图书与用900元购进的B类图书册数相同.
(1)求每本A类图书和每本B类图书的价格各为多少元?
(2)根据学校实际情况,需从书店一次性购买A、B两类图书共300册,购买时得知:一次性购买A、B两类图书超过100册时,A类图书九折优惠(B类图书按原价销售),若该校此次用于购买A、B两类图书的总费用不超过5100元,那么最多可以购买多少本A类图书?
参考答案
一.分式方程的定义
1.解:A、该方程属于一元一次方程,不符合题意.
B、该方程属于分式方程,符合题意.
C、该方程属于一元二次方程,不符合题意.
D、该方程属于一元一次方程,不符合题意.
故选:B.
2.解:A、该方程是一元一次方程,故本选项不符合题意;
B、该方程符合分式方程的定义,故本选项符合题意;
C、该方程是一元一次方程,故本选项不符合题意;
D、该方程是二元一次方程,故本选项不符合题意;
故选:B.
3.解:A、方程分母中不含未知数,故不是分式方程;
B、方程分母中含未知数x,故是分式方程;
C、方程分母中不含表示未知数的字母,π是常数;
D、方程分母中不含未知数,故不是分式方程.
故选:B.
4.解:A、C选项项中的方程分母中不含未知数,故不是分式方程;
B选项不是方程.
D选项中的方程分母中含未知数x,故是分式方程,
故选:D.
5.解:关于x的方程②,③中,分母中都含有字母,都是分式方程;
关于x的方程①,④中,分母中不含未知数,故不是分式方程.
综上所述,是分式方程的有②、③,共2个.
故选:C.
二.分式的方程的解
6.解:分式方程去分母得:2x﹣m=x﹣1,
解得:x=m﹣1,
由分式方程的解为正数,得到m﹣1>0,且m﹣1≠1,
解得:m>1且m≠2,
故答案为:m>1且m≠2.
7.解:去分母得:2x+a=x+1,
解得:x=1﹣a,
由解为负数,得到1﹣a<0,且1﹣a≠﹣1,
解得:a>1且a≠2,
故答案为:a>1且a≠2
8.解:方程去分母得:ax=4+x﹣2
解得:(a﹣1)x=2,
∴当a﹣1=0即a=1时,整式方程无解,分式方程无解;
当a≠1时,x=
x=2时分母为0,方程无解,
即=2,
∴a=2时方程无解.
故选:C.
9.解:分式方程去分母得:1﹣ax﹣3﹣2+x=0,即(1﹣a)x=4,
由分式方程有整数解,得到1﹣a≠0,
解得:x=,
不等式组整理得:,即﹣3≤x<,
由不等式组有且只有3个整数解,得到﹣1<≤0,
解得:﹣1<a≤,
由x为整数,且≠2,得到1﹣a=±1,﹣2,±4,
解得:a=0,
则符合条件的所有整数a的个数为1,
故选:A.
10.解:不等式组整理得:,
由不等式组有解,得到﹣5≤x<a,
解得:a>﹣5,
,
分式方程去分母得:ax﹣x+2=﹣3x,
解得:x=,
∵关于x的分式方程的解为非负数,
∴≥0,解得a≤1,
当a=﹣1时,x=1(不合题意舍去)
∴﹣5<a≤1,
∵a为整数,
∴a=﹣4,﹣3,﹣2,0,1,
则满足题意的整数a的值的和是﹣2﹣3﹣4+0+1=﹣8.
故选:D.
三.解分式方程、换元法
11.解:分式方程的最简公分母为(x﹣1)(x+1),
方程两边乘以(x﹣1)(x+1),得整式方程2(x﹣1)+3(x+1)=6,
解得:x=1,
经检验x=1是增根,分式方程无解.
故选:D.
12.解:去分母得:3﹣2(x+3)=x﹣3,
去括号得:3﹣2x﹣6=x﹣3,
移项合并得:﹣3x=0,
解得:x=0,
经检验x=0是分式方程的解.
13.解:﹣=1
(x+1)2﹣4=x2﹣1
x2+2x+1﹣4=x2﹣1
x=1,
检验:把x=1代入x2﹣1=1﹣1=0,
∴x=1不是原方程的根,原方程无解.
14.解:原方程变形为:﹣1=,
方程两边同乘以3(x+1),得3x﹣3x﹣3=2x,
解得:x=﹣1.5,
经检验,x=﹣1.5是原方程的根.
15.解:=方程的两边同乘(x﹣1)(x﹣3)得,
2(x﹣1)=x﹣3解得,
x=﹣1
检验:把x=﹣1代入(x﹣1)(x﹣3)≠0
∴原方程的解为:x=﹣1
16.解:设x2﹣x=y,原方程等价于y﹣1+=0,
两边都乘以y,得
y2﹣y+2=0,
故选:C.
17.解:设=y,则原方程化为2y2+3y﹣5=0.
故选:A.
18.解:x2+﹣2+x﹣﹣2=0
∴(x﹣)2+(x﹣)﹣2=0
解得x﹣=﹣2或1.
经检验,x﹣=1和x﹣=﹣2均有实数根.
所以x﹣=﹣2或1.
故选:D.
19.解:根据题意得:设,
则=,
∴原方程可变为;
故答案为.
20.解:根据等式的性质原方程可整理为x2﹣3x++4=0.
把y=x2﹣3x代入可得y++4=0,
去分母得y2+4y+3=0.
四.分式方程的增根
21.解:方程两边都乘x﹣1,
得:3=x﹣1+k,
∵原方程有增根,
∴最简公分母x﹣1=0,
解得x=1,
当x=1时,k=3.
故k的值为3.
故选:A.
22.解:方程两边都乘x﹣4,
得3﹣(x+m)=x﹣4,
∵原方程有增根,
∴最简公分母x﹣4=0,
解得x=4,
当x=4时,3﹣(4+m)=4﹣4,
m=﹣1,
故选:B.
23.解:去分母得:x+2=m,
由分式方程有增根,得到x﹣2=0,即x=2,
把x=2代入整式方程得:m=4,
则m的值与增根x的值分别是m=4,x=2,
故选:B.
24.解:(1)当a=3时,原方程为﹣=1,
方程两边同时乘以(x﹣1)得:3x+1+2=x﹣1,
解这个整式方程得:x=﹣2,
检验:将x=﹣2代入x﹣1=﹣2﹣1=﹣3≠0,
∴x=﹣2是原方程的解;
(2)方程两边同时乘以(x﹣1)得ax+1+2=x﹣1,即(a﹣1)x=﹣4,
当a≠1时,若原方程有增根,则x﹣1=0,
解得:x=1,
将x=1代入整式方程得:a+1+2=0,
解得:a=﹣3,
综上,a的值为﹣3.
25.解:原方程化为+=,
方程两边同时乘以(x+2)(x﹣2)
得2(x+2)+mx=3(x﹣2),
整理得(m﹣1)x+10=0,
∵关于x的方程 +=会产生增根,
∴(x+2)(x﹣2)=0,
∴x=﹣2 或x=2,
∴当x=﹣2时,(m﹣1)×(﹣2)+10=0,解得m=6,
当x=2时,(m﹣1)×2+10=0,解得m=﹣4,
∴m=﹣4或m=6时,原方程会产生增根.
五.由实际问题抽象出分式方程
26.解:若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
27.解:设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得:
×2=,
故选:A.
28.解:设原计划速度为x千米/小时,
根据题意得:
原计划的时间为:,
实际的时间为:+1,
∵实际比原计划提前40分钟到达目的地,
∴+1=﹣,
故选:C.
29.解:设汽车在线路一上行驶的平均速度为xkm/h,则在线路二上行驶的平均速度为1.8xkm/h,
由题意得:=+,
故选:A.
30.解:顺流所用的时间为:,逆流所用的时间为:.所列方程为:=9.
31.解:设乙每小时做x个零件,甲每小时做(x+6)个零件,
根据题意得:,
解得:x=12,
经检验,x=12是原方程的解,且符合题意,
∴x+6=18.
答:乙每小时做12个零件,甲每小时做18个零件.
32.解:设规定日期为x天,
根据题意,得2(+)+×(x﹣2)=1
解这个方程,得x=6
经检验,x=6
是原方程的解.
∴原方程的解是x=6.
答:规定日期是6天.
33.解:设前一小时的行驶速度为xkm/h,根据题意可得:
+1=﹣,
解得:x=60,
检验得:x=60是原方程的根,
答:前一小时的行驶速度为60km/h.
34.解:(1)设乙条生产线每天的产能是x万个,则甲条生产线每天的产能是2x万个,依题意有
﹣=2,
解得x=20,
经检验,x=20是原方程的解,
2x=2×20=40,
故甲条生产线每天的产能是40万个,乙条生产线每天的产能是20万个;
(2)设安排乙生产线生产y天,依题意有
0.5y+1.2×≤40,
解得y≥32.
故至少应安排乙生产线生产32天;
(3)(40+20)×3+[40×(1+50%)+20×2]×13
=180+1300
=1480(万个),
1440万个<1480万个,
故再满负荷生产13天能完成任务.
35.解:(1)设A种型号健身器材的单价为x元/套,B种型号健身器材的单价为1.5x元/套,
根据题意,可得:,
解得:x=360,
经检验x=360是原方程的根,
1.5×360=540(元),
因此,A,B两种健身器材的单价分别是360元,540元;
(2)设购买A种型号健身器材m套,则购买B种型号的健身器材(50﹣m)套,
根据题意,可得:360m+540(50﹣m)≤21000,
解得:m≥33,
因此,A种型号健身器材至少购买34套.
36.解:设原计划每天铺设管道x米,则实际每天铺设管道1.2x米,
由题意,得﹣=2.
解得:x=60.
经检验,x=60是原方程的解.且符合题意.
答:原计划每天铺设管道60米.
37.解:(1)设第一次购买了此种服装x件,那么第二次购进2x件,
依题意得,
解之得x=30,
经检验x=30是方程的解,
答:第一次购买了此种服装30件;
(2)∵第一次购买了此种服装30件,盈利46×30﹣960=420元;
∴第二次购买了此种服装60件,46×(60﹣20)+46×0.9×20﹣2220=448元;
∴两次出售服装共盈利420+448=868元.
38.解:(1)设B种书架的单价为x元,根据题意,得.
解得x=80.
经检验:x=80是原分式方程的解.
∴x+20=100.
答:购买A种书架需要100元,B种书架需要80元.
(2)设准备购买m个A种书架,根据题意,得100m+80(15﹣m)≤1400.
解得m≤10.
答:最多可购买10个A种书架.
39.解:(1)设每个B类摊位的占地面积为x平方米,则每个A类摊位占地面积为(x+2)平方米,
根据题意得:,
解得:x=3,
经检验x=3是原方程的解,
所以3+2=5,
答:每个A类摊位占地面积为5平方米,每个B类摊位的占地面积为3平方米;
(2)解法一:设建A摊位a个,建造这90个摊位的费用为y元,则建B摊位(90﹣a)个,
由题意得:y=5a×40+3×30(90﹣a)=110a+8100,
∵110>0,
∴y随a的增大而增大,
∵90﹣a≥3a,
解得a≤22.5,
∵a为整数,
∴当a取最大值22时,费用最大,
此时最大费用为:110×22+8100=10520;
解法二:设建A摊位a(a为整数)个,则建B摊位(90﹣a)个,
由题意得:90﹣a≥3a,
解得a≤22.5,
∵建A类摊位每平方米的费用为40元,建B类摊位每平方米的费用为30元,
∴要想使建造这90个摊位有最大费用,所以要多建造A类摊位,即a取最大值22时,费用最大,
此时最大费用为:22×40×5+30×(90﹣22)×3=10520,
答:建造这90个摊位的最大费用是10520元.
40.解:(1)设每本A类图书的价格是x元,则每本B类图书的价格是(x﹣5)元,根据题意可得:
,
解得:x=20,
经检验x=20是方程的解,所以x﹣5=20﹣5=15,
答:每本A类图书的价格是20元,每本B类图书的价格是15元;
(2)设该校A类图书y本,则B类图书(300﹣y),
根据题意可得:20×90%y+15×(300﹣y)≤5100,
解得:y≤200,
答:最多可以购买200本A类图书.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
