六年级数学下册教案:5 数学广角——鸽巢问题(人教版)
文档属性
| 名称 | 六年级数学下册教案:5 数学广角——鸽巢问题(人教版) | 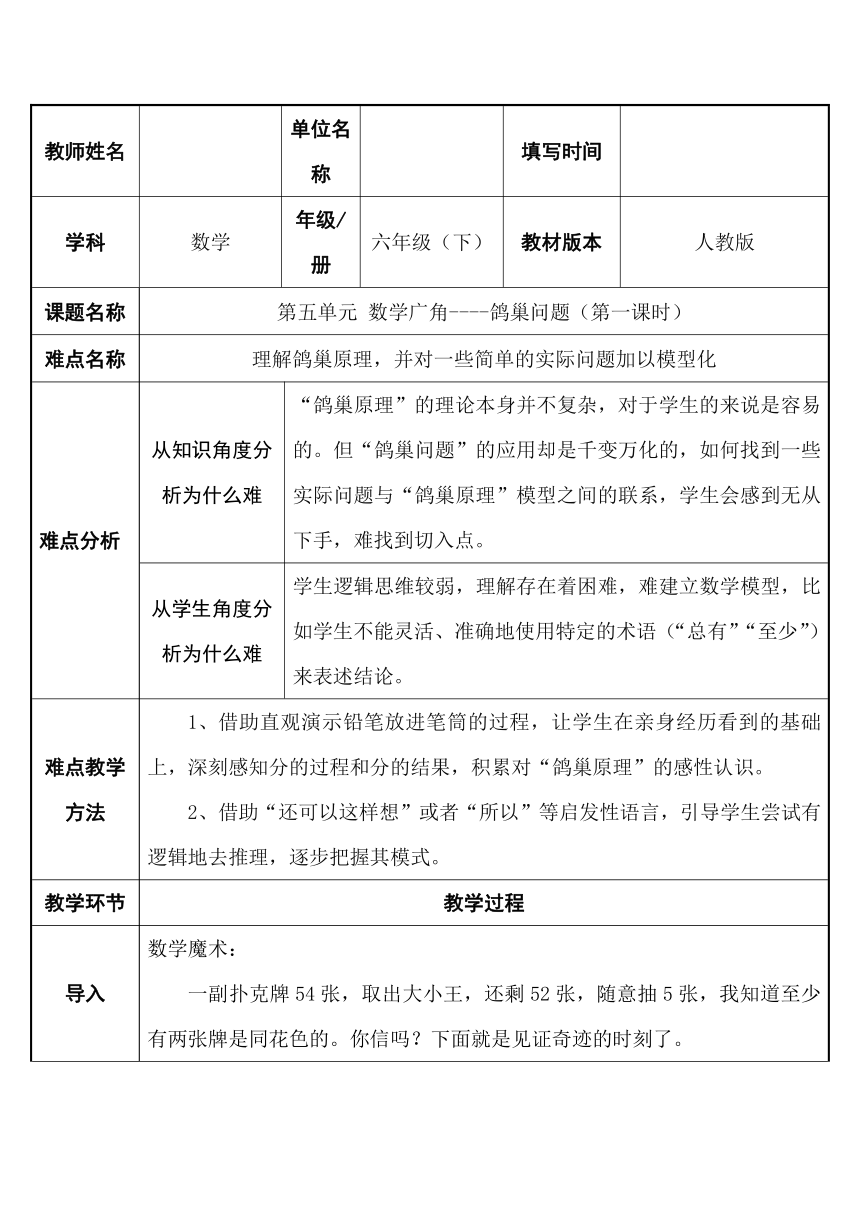 | |
| 格式 | docx | ||
| 文件大小 | 45.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 10:40:44 | ||
图片预览


文档简介
教师姓名
单位名称
填写时间
学科
数学
年级/册
六年级(下)
教材版本
人教版
课题名称
第五单元 数学广角----鸽巢问题(第一课时)
难点名称
理解鸽巢原理,并对一些简单的实际问题加以模型化
难点分析
从知识角度分析为什么难
“鸽巢原理”的理论本身并不复杂,对于学生的来说是容易的。但“鸽巢问题”的应用却是千变万化的,如何找到一些实际问题与“鸽巢原理”模型之间的联系,学生会感到无从下手,难找到切入点。
从学生角度分析为什么难
学生逻辑思维较弱,理解存在着困难,难建立数学模型,比如学生不能灵活、准确地使用特定的术语(“总有”“至少”)来表述结论。
难点教学方法
借助直观演示铅笔放进笔筒的过程,让学生在亲身经历看到的基础上,深刻感知分的过程和分的结果,积累对“鸽巢原理”的感性认识。
借助“还可以这样想”或者“所以”等启发性语言,引导学生尝试有逻辑地去推理,逐步把握其模式。
教学环节
教学过程
导入
数学魔术:
一副扑克牌54张,取出大小王,还剩52张,随意抽5张,我知道至少有两张牌是同花色的。你信吗?下面就是见证奇迹的时刻了。
知识讲解
(难点突破)
一、把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。为什么呢?
理解“总有”和“至少”的意思。
摆一摆、看一看、探一探
第①种摆法:可以把4支铅笔全部放到第一个笔筒里,这种摆法记为(4,0,0),也可以这样摆(0,4,0),还可以这样摆(0,0,4),虽然摆放的顺序不同,但情况都是一样的。
第②种摆法:记为(3,1,0)
第③种摆法:记为(2,2,0)
第④种摆法:记为(2,1,1)
验证4种摆法是否都符合结论,引出列举法。
假设法:还可以这样摆,先把3支铅笔放到3个笔筒中,每个笔筒放一支,也就是平均分,剩下的一支铅笔,可以任意的放入其中的笔筒中。这种摆法与刚刚第4种摆法是一样的。平均分能让每个笔筒的笔尽可能的少一些,如果这样都符合条件,那其它的摆法,肯定也符合条件。
二、把5支铅笔放进4个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设先把4支铅笔放进笔筒里,平均分,让每个笔筒都有1支铅笔,剩下的1支铅笔任意放进笔筒中,所以把5支铅笔放进4个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
三、把6支铅笔放进5个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设先把5支铅笔放进笔筒里,平均分,让每个笔筒都有1支铅笔,剩下的1支铅笔任意放进笔筒中,所以把6支铅笔放进5个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
四、把n+1支铅笔放进n个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设先把n支铅笔放进n个笔筒里,平均分,让每个笔筒都有1支铅笔,剩下的1支铅笔任意放进笔筒中,所以把n+1支铅笔放进n个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设法与列举法两种方法优越性与局限性的比较。
小结
只要放的铅笔数比笔筒数多1,不管怎么放,总有一个笔筒里至少有2支铅笔。
七、用假设法说说以下两句话能得到什么结论。
①把10个苹果放进9个抽屉
②6只鸽子飞进5个鸽巢
八、数学历史
介绍“狄利克雷原理”。
课堂练习
(难点巩固)
5只鸽子飞进3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?
假设法:假设每个鸽笼都有一只鸽子飞进去,剩下2只鸽子可以都飞进同一鸽笼里,或者分别飞进不同的鸽笼里,所以5只鸽子飞进3个鸽笼,总有一个鸽笼至少飞进了两只鸽子。
小结
只要放的铅笔数比笔筒数多1,不管怎么放,总有一个笔筒里至少有2支铅笔。
单位名称
填写时间
学科
数学
年级/册
六年级(下)
教材版本
人教版
课题名称
第五单元 数学广角----鸽巢问题(第一课时)
难点名称
理解鸽巢原理,并对一些简单的实际问题加以模型化
难点分析
从知识角度分析为什么难
“鸽巢原理”的理论本身并不复杂,对于学生的来说是容易的。但“鸽巢问题”的应用却是千变万化的,如何找到一些实际问题与“鸽巢原理”模型之间的联系,学生会感到无从下手,难找到切入点。
从学生角度分析为什么难
学生逻辑思维较弱,理解存在着困难,难建立数学模型,比如学生不能灵活、准确地使用特定的术语(“总有”“至少”)来表述结论。
难点教学方法
借助直观演示铅笔放进笔筒的过程,让学生在亲身经历看到的基础上,深刻感知分的过程和分的结果,积累对“鸽巢原理”的感性认识。
借助“还可以这样想”或者“所以”等启发性语言,引导学生尝试有逻辑地去推理,逐步把握其模式。
教学环节
教学过程
导入
数学魔术:
一副扑克牌54张,取出大小王,还剩52张,随意抽5张,我知道至少有两张牌是同花色的。你信吗?下面就是见证奇迹的时刻了。
知识讲解
(难点突破)
一、把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。为什么呢?
理解“总有”和“至少”的意思。
摆一摆、看一看、探一探
第①种摆法:可以把4支铅笔全部放到第一个笔筒里,这种摆法记为(4,0,0),也可以这样摆(0,4,0),还可以这样摆(0,0,4),虽然摆放的顺序不同,但情况都是一样的。
第②种摆法:记为(3,1,0)
第③种摆法:记为(2,2,0)
第④种摆法:记为(2,1,1)
验证4种摆法是否都符合结论,引出列举法。
假设法:还可以这样摆,先把3支铅笔放到3个笔筒中,每个笔筒放一支,也就是平均分,剩下的一支铅笔,可以任意的放入其中的笔筒中。这种摆法与刚刚第4种摆法是一样的。平均分能让每个笔筒的笔尽可能的少一些,如果这样都符合条件,那其它的摆法,肯定也符合条件。
二、把5支铅笔放进4个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设先把4支铅笔放进笔筒里,平均分,让每个笔筒都有1支铅笔,剩下的1支铅笔任意放进笔筒中,所以把5支铅笔放进4个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
三、把6支铅笔放进5个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设先把5支铅笔放进笔筒里,平均分,让每个笔筒都有1支铅笔,剩下的1支铅笔任意放进笔筒中,所以把6支铅笔放进5个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
四、把n+1支铅笔放进n个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设先把n支铅笔放进n个笔筒里,平均分,让每个笔筒都有1支铅笔,剩下的1支铅笔任意放进笔筒中,所以把n+1支铅笔放进n个笔筒中,不管怎么放,总有一个笔筒里至少有2支铅笔。
假设法与列举法两种方法优越性与局限性的比较。
小结
只要放的铅笔数比笔筒数多1,不管怎么放,总有一个笔筒里至少有2支铅笔。
七、用假设法说说以下两句话能得到什么结论。
①把10个苹果放进9个抽屉
②6只鸽子飞进5个鸽巢
八、数学历史
介绍“狄利克雷原理”。
课堂练习
(难点巩固)
5只鸽子飞进3个鸽笼,总有一个鸽笼至少飞进了2只鸽子。为什么?
假设法:假设每个鸽笼都有一只鸽子飞进去,剩下2只鸽子可以都飞进同一鸽笼里,或者分别飞进不同的鸽笼里,所以5只鸽子飞进3个鸽笼,总有一个鸽笼至少飞进了两只鸽子。
小结
只要放的铅笔数比笔筒数多1,不管怎么放,总有一个笔筒里至少有2支铅笔。
