1.4 正弦函数、余弦函数的图象(共22张PPT)
文档属性
| 名称 | 1.4 正弦函数、余弦函数的图象(共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
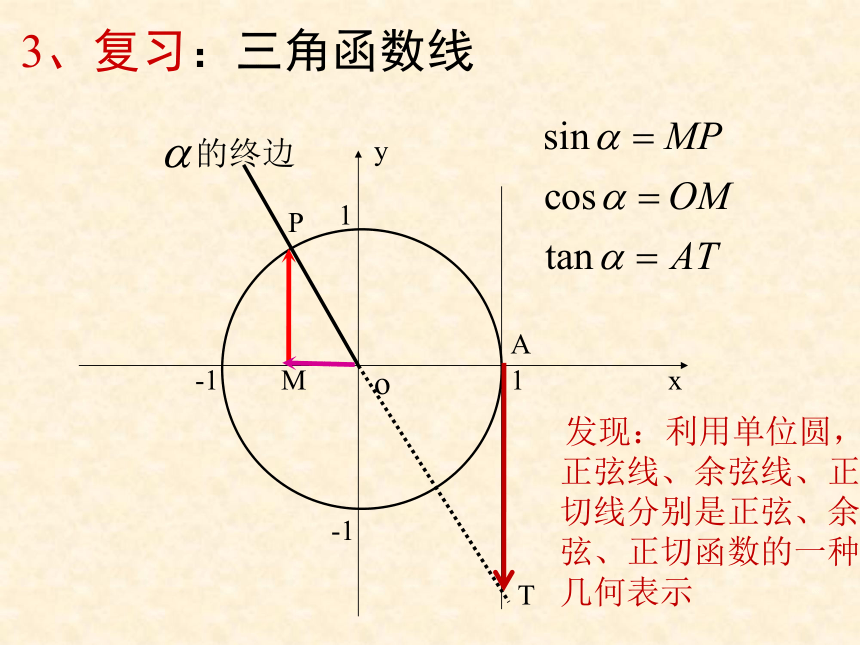
3、复习:三角函数线
x
y
o
P
M
T
1
A
的终边
-1
-1
1
发现:利用单位圆,正弦线、余弦线、正切线分别是正弦、余弦、正切函数的一种几何表示
课前思考1:既然一个确定的角对应着唯一确定的正(余)弦值,那么,任意给定一个实数
,有唯一确定的值
与之对应,由这个对应法则所确定函数
叫做正弦函数(余弦函数),其定义域为
则函数图象怎么画呢?
思考2:比如正弦函数
当自变量
时,函数值为
,那么对应到坐标系中的点
怎么取呢?
§1.4.1正弦函数、余弦函数的图象
课前复习:
1、引入弧度制后,实数与角建立一一对应关系,比如
2、回顾三角函数的定义:
都是以角为自变量,以单位圆上点的坐标或坐标比值为函数值的函数
1
-1
0
y
x
●
●
●
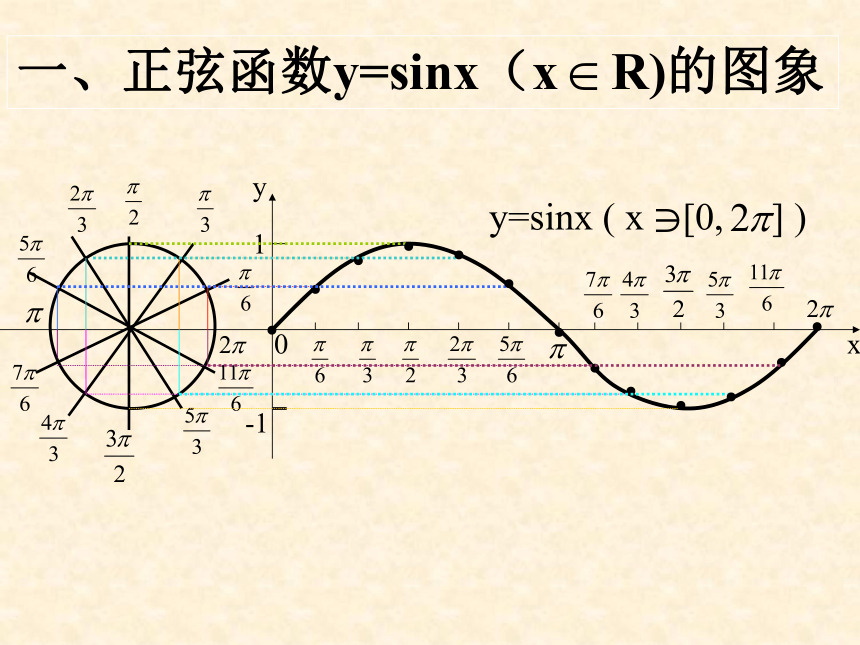
一、正弦函数y=sinx(x
R)的图象
y=sinx
(
x
[0,
]
)
●
●
●
●
●
●
●
●
●
●
-
-
-1
1
-
-1
在函数
的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
在精度要求不高的情况下,我们可以利用这5个点画出函数
的简图,一般把这种画图方法叫“五点法”。
因为终边相同的角的三角函数值相同,所以y=sinx,x∈R的图象在
…与y=sinx,x∈[0,2π]的图象相同
-
-
-
-
-
-
-
-
-
1
-1
思考:
正弦曲线:
x
y
1
-1
x
y
1
-1
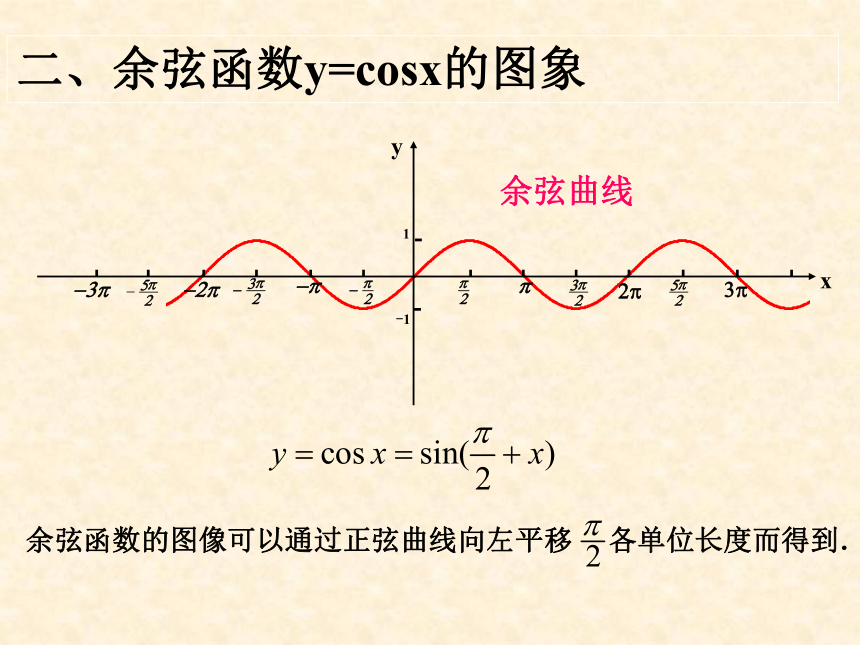
余弦曲线
余弦函数的图像可以通过正弦曲线向左平移
各单位长度而得到.
二、余弦函数y=cosx的图象
-
-
-
-1
1
-
-1
在函数
的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
余弦曲线:
x
y
1
-1
二、正弦函数的“五点画图法”
(0,0)、(
,
1)、(
,0)、(
,-1)、
(2
,0)
0
x
y
1
-1
●
●
●
●
●
余弦函数的“五点画图法”
(0,1)、(
,0)、(
,-1)、(
,0)、(
,
1)
o
x
y
●
●
●
●
●
1
-1
正弦曲线:
余弦曲线:
x
y
1
-1
x
y
1
-1
例2
例1:画出下列函数的简图
(1)y=1+sinx,
x
[0,
]
(2)y=
-
cosx,
x
[0,
]
解:(1)按五个关键点列表
x
sinx
1+sinx
0
0
1
0
-1
0
1
2
1
0
1
o
x
y
1
2
●
●
●
●
●
y=1+sinx
x
[0,
]
(2)按五个关键点列表
x
cosx
-cosx
0
1
0
-1
0
1
-1
0
1
0
-1
o
x
y
1
●
●
●
●
●
y=-cosx
x
[0,
]
-1
思考:
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系?
2、函数y=-cosx的图象与函数y=cosx的图象有什么关系?
o
-1
1
2
y=sinx
x
[0,
]
y=1+sinx
x
[0,
]
y
x
y
x
o
-1
1
y=cosx
x
[0,
]
y=-cosx
x
[0,
]
例2:观察正弦曲线和余弦曲线,写出满足下列条件x的区间:
图像
小结:
1、正弦函数、余弦函数图象以及五点法
作简图
2、正余弦函数的定义域、值域以及对称性
3、复习:三角函数线
x
y
o
P
M
T
1
A
的终边
-1
-1
1
发现:利用单位圆,正弦线、余弦线、正切线分别是正弦、余弦、正切函数的一种几何表示
课前思考1:既然一个确定的角对应着唯一确定的正(余)弦值,那么,任意给定一个实数
,有唯一确定的值
与之对应,由这个对应法则所确定函数
叫做正弦函数(余弦函数),其定义域为
则函数图象怎么画呢?
思考2:比如正弦函数
当自变量
时,函数值为
,那么对应到坐标系中的点
怎么取呢?
§1.4.1正弦函数、余弦函数的图象
课前复习:
1、引入弧度制后,实数与角建立一一对应关系,比如
2、回顾三角函数的定义:
都是以角为自变量,以单位圆上点的坐标或坐标比值为函数值的函数
1
-1
0
y
x
●
●
●
一、正弦函数y=sinx(x
R)的图象
y=sinx
(
x
[0,
]
)
●
●
●
●
●
●
●
●
●
●
-
-
-1
1
-
-1
在函数
的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
在精度要求不高的情况下,我们可以利用这5个点画出函数
的简图,一般把这种画图方法叫“五点法”。
因为终边相同的角的三角函数值相同,所以y=sinx,x∈R的图象在
…与y=sinx,x∈[0,2π]的图象相同
-
-
-
-
-
-
-
-
-
1
-1
思考:
正弦曲线:
x
y
1
-1
x
y
1
-1
余弦曲线
余弦函数的图像可以通过正弦曲线向左平移
各单位长度而得到.
二、余弦函数y=cosx的图象
-
-
-
-1
1
-
-1
在函数
的图象上,起关键作用的点有:
最高点:
最低点:
与x轴的交点:
余弦曲线:
x
y
1
-1
二、正弦函数的“五点画图法”
(0,0)、(
,
1)、(
,0)、(
,-1)、
(2
,0)
0
x
y
1
-1
●
●
●
●
●
余弦函数的“五点画图法”
(0,1)、(
,0)、(
,-1)、(
,0)、(
,
1)
o
x
y
●
●
●
●
●
1
-1
正弦曲线:
余弦曲线:
x
y
1
-1
x
y
1
-1
例2
例1:画出下列函数的简图
(1)y=1+sinx,
x
[0,
]
(2)y=
-
cosx,
x
[0,
]
解:(1)按五个关键点列表
x
sinx
1+sinx
0
0
1
0
-1
0
1
2
1
0
1
o
x
y
1
2
●
●
●
●
●
y=1+sinx
x
[0,
]
(2)按五个关键点列表
x
cosx
-cosx
0
1
0
-1
0
1
-1
0
1
0
-1
o
x
y
1
●
●
●
●
●
y=-cosx
x
[0,
]
-1
思考:
1、函数y=1+sinx的图象与函数y=sinx的图象有什么关系?
2、函数y=-cosx的图象与函数y=cosx的图象有什么关系?
o
-1
1
2
y=sinx
x
[0,
]
y=1+sinx
x
[0,
]
y
x
y
x
o
-1
1
y=cosx
x
[0,
]
y=-cosx
x
[0,
]
例2:观察正弦曲线和余弦曲线,写出满足下列条件x的区间:
图像
小结:
1、正弦函数、余弦函数图象以及五点法
作简图
2、正余弦函数的定义域、值域以及对称性
