第九章 图形的相似专项训练:相似三角形的判定和性质的综合应用(含答案)
文档属性
| 名称 | 第九章 图形的相似专项训练:相似三角形的判定和性质的综合应用(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 22:32:34 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
专项训练
相似三角形的判定和性质的综合应用
一、选择题
1.如图所示,在平行四边形ABCD中,E为BC的中点,连接AE交对角线BD于F,若BF=2,则FD等于( )
A.2 B.3 C.4 D.6
2.如图所示,在△ABC中,∠A=60°,BE、CF分别是AC、AB边上的高,连接EF,则EF:BC等于( )
A.1:2 B.2:3 C.1:4 D.2:5
3.如图所示,在△ABC中,AB=AC=6,D是AC的中点,E是边BC上一点,BE=,∠AED=∠B,则CE的长为( )
A. B. C. D.
4.如图所示,在等边三角形ABC中,D,E,F分别是边BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比为( )
A.1:3 B.2:3 C.:2 D.:3
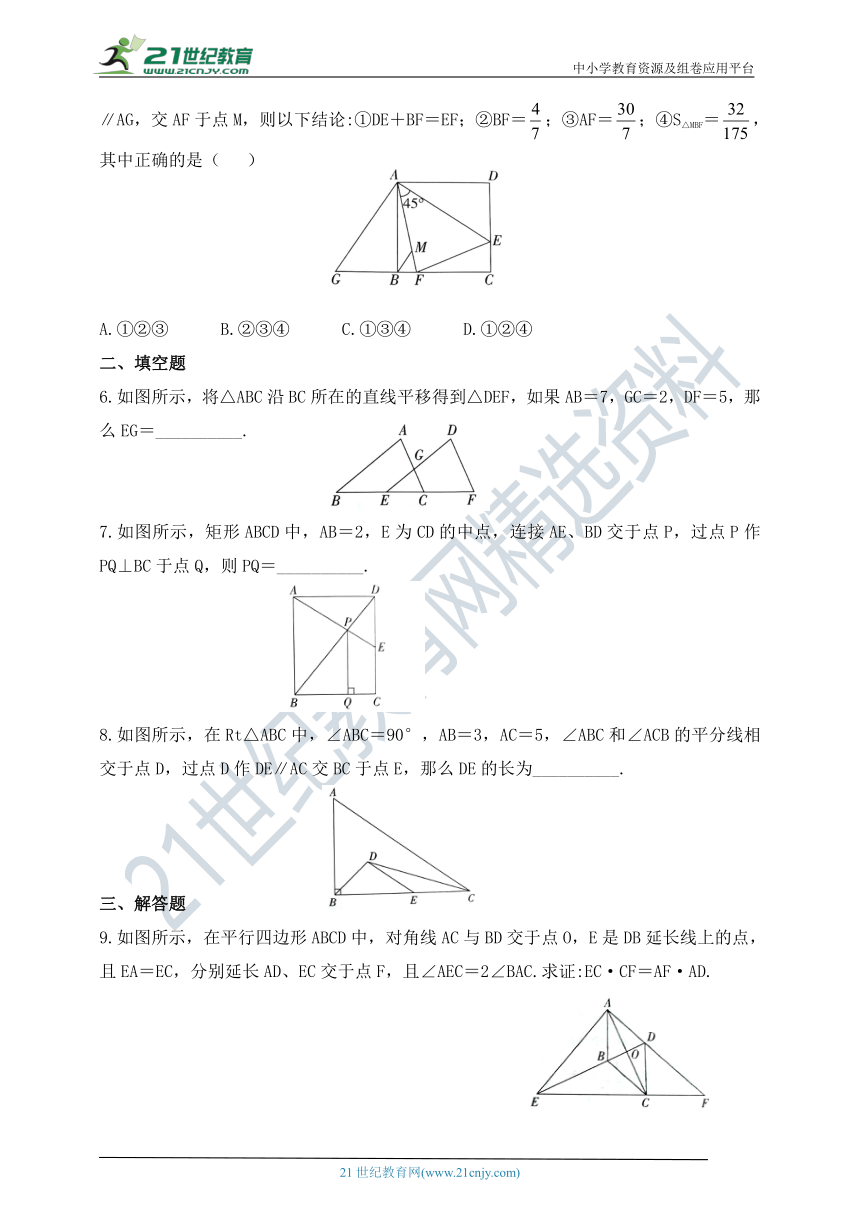
5.如图所示,在正方形ABCD中,AD=4,E,F分别是CD,BC上的点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF;②BF=;③AF=;④S△MBF=,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题
6.如图所示,将△ABC沿BC所在的直线平移得到△DEF,如果AB=7,GC=2,DF=5,那么EG=__________.
7.如图所示,矩形ABCD中,AB=2,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=__________.
8.如图所示,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,∠ABC和∠ACB的平分线相交于点D,过点D作DE∥AC交BC于点E,那么DE的长为__________.
三、解答题
9.如图所示,在平行四边形ABCD中,对角线AC与BD交于点O,E是DB延长线上的点,且EA=EC,分别延长AD、EC交于点F,且∠AEC=2∠BAC.求证:EC·CF=AF·AD.
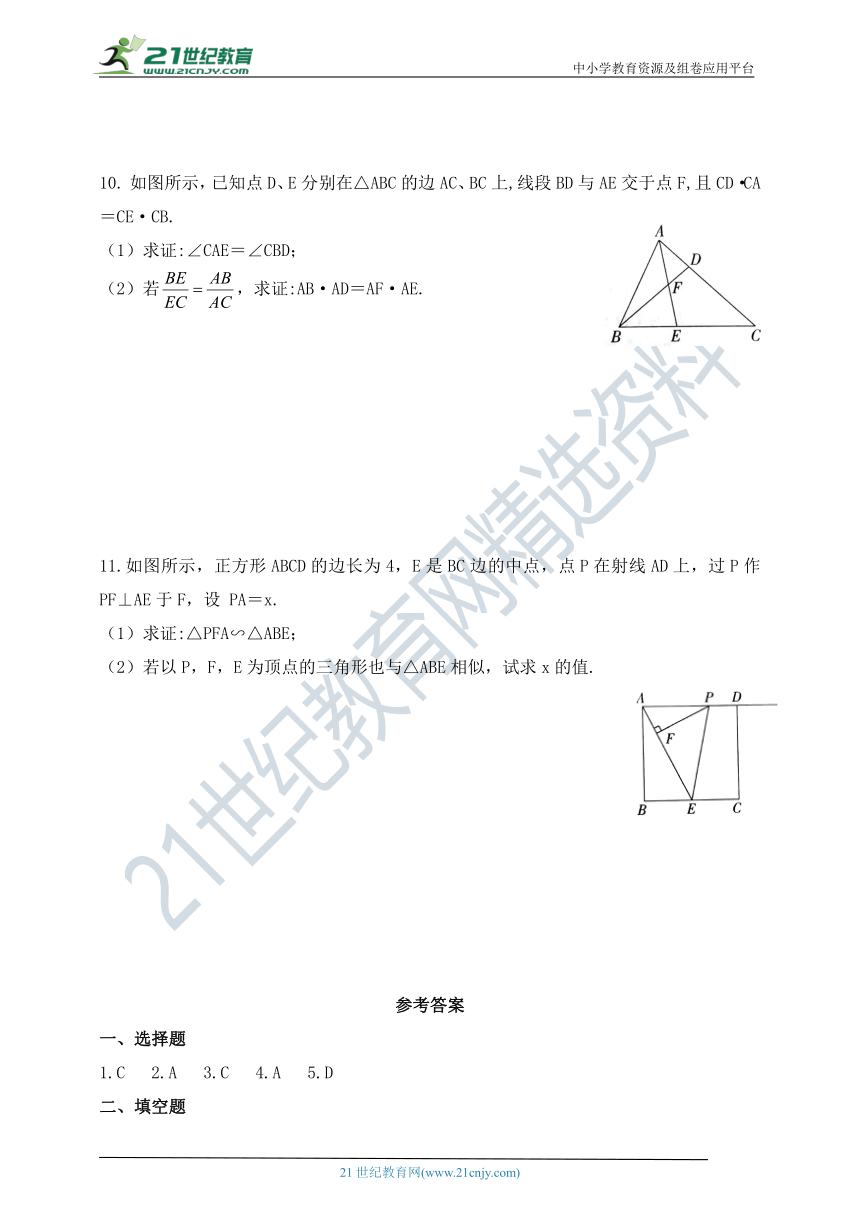
如图所示,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CD·CA=CE·CB.
(1)求证:∠CAE=∠CBD;
(2)若,求证:AB·AD=AF·AE.
11.如图所示,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设 PA=x.
(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值.
参考答案
一、选择题
1.C 2.A 3.C 4.A 5.D
二、填空题
6. 7. 8.
三、解答题
9.证明 ∵四边形ABCD是平行四边形,∴OA=OC,
又∵EA=EC,∴EO⊥AC,∴四边形ABCD是菱形,
∴∠BAC=∠BCA=∠DAC=∠DCA,∴∠CDF=∠DAC+∠DCA=2∠BAC,
∵∠AEC=2∠BAC,∴∠CDF=∠AEC,∵∠F=∠F,∴△FCD∽△FAE,∴,
∵CD=AD,EA=EC,∴,即EC·CF=AF·AD.
10.证明(1)∵CD·CA=CE·CB,∴,
∵∠ECA=∠DCB,∴△CAE△CBD,∴∠CAE=∠CBD.
(2)如图,过点C作CG∥AB,交AE的延长线于点G.
易得△ABE∽△GCE,∴,
又∵,∴,∴CG=CA,∴∠G=∠CAG,
∵AB∥CG,∴∠G=∠BAG,∴∠CAG=∠BAG.
∵∠CAE=∠CBD,∠AFD=∠BFE,∴∠ADF=∠BEF,∴△ADF∽△AEB,
∴,∴AB·AD=AF·AE.
11.解析(1)证明∵四边形ABCD是正方形,∴AD∥BC,且∠ABE=∠BAP=90°.
∴∠PAF=∠AEB,又∵PF⊥AE,∴∠PFA=∠ABE=90°,∴△PFA∽△ABE.
(2)①当△EFP∽△ABE时,∠PEF=∠EAB,∴PE∥AB,又AP∥BE,∠B=90°,
∴四边形ABEP为矩形,∴PA=EB=2,即x=2
②当△PFE∽△ABE时,∠PEF=∠AEB,
∵∠PAF=∠AEB,∴∠PEF=∠PAF,∴PE=PA∵PF⊥AE,∴F为AE的中点.
∵AE=,∴EF=AE=.
∵△PFE∽△ABE,∴,即,∴PE=5,
∴PA=5,即x=5.
综上所述,x的值为2或5.
_21?????????è?????(www.21cnjy.com)_
专项训练
相似三角形的判定和性质的综合应用
一、选择题
1.如图所示,在平行四边形ABCD中,E为BC的中点,连接AE交对角线BD于F,若BF=2,则FD等于( )
A.2 B.3 C.4 D.6
2.如图所示,在△ABC中,∠A=60°,BE、CF分别是AC、AB边上的高,连接EF,则EF:BC等于( )
A.1:2 B.2:3 C.1:4 D.2:5
3.如图所示,在△ABC中,AB=AC=6,D是AC的中点,E是边BC上一点,BE=,∠AED=∠B,则CE的长为( )
A. B. C. D.
4.如图所示,在等边三角形ABC中,D,E,F分别是边BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比为( )
A.1:3 B.2:3 C.:2 D.:3
5.如图所示,在正方形ABCD中,AD=4,E,F分别是CD,BC上的点,且∠EAF=45°,EC=1,将△ADE绕点A沿顺时针方向旋转90°后与△ABG重合,连接EF,过点B作BM∥AG,交AF于点M,则以下结论:①DE+BF=EF;②BF=;③AF=;④S△MBF=,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题
6.如图所示,将△ABC沿BC所在的直线平移得到△DEF,如果AB=7,GC=2,DF=5,那么EG=__________.
7.如图所示,矩形ABCD中,AB=2,E为CD的中点,连接AE、BD交于点P,过点P作PQ⊥BC于点Q,则PQ=__________.
8.如图所示,在Rt△ABC中,∠ABC=90°,AB=3,AC=5,∠ABC和∠ACB的平分线相交于点D,过点D作DE∥AC交BC于点E,那么DE的长为__________.
三、解答题
9.如图所示,在平行四边形ABCD中,对角线AC与BD交于点O,E是DB延长线上的点,且EA=EC,分别延长AD、EC交于点F,且∠AEC=2∠BAC.求证:EC·CF=AF·AD.
如图所示,已知点D、E分别在△ABC的边AC、BC上,线段BD与AE交于点F,且CD·CA=CE·CB.
(1)求证:∠CAE=∠CBD;
(2)若,求证:AB·AD=AF·AE.
11.如图所示,正方形ABCD的边长为4,E是BC边的中点,点P在射线AD上,过P作PF⊥AE于F,设 PA=x.
(1)求证:△PFA∽△ABE;
(2)若以P,F,E为顶点的三角形也与△ABE相似,试求x的值.
参考答案
一、选择题
1.C 2.A 3.C 4.A 5.D
二、填空题
6. 7. 8.
三、解答题
9.证明 ∵四边形ABCD是平行四边形,∴OA=OC,
又∵EA=EC,∴EO⊥AC,∴四边形ABCD是菱形,
∴∠BAC=∠BCA=∠DAC=∠DCA,∴∠CDF=∠DAC+∠DCA=2∠BAC,
∵∠AEC=2∠BAC,∴∠CDF=∠AEC,∵∠F=∠F,∴△FCD∽△FAE,∴,
∵CD=AD,EA=EC,∴,即EC·CF=AF·AD.
10.证明(1)∵CD·CA=CE·CB,∴,
∵∠ECA=∠DCB,∴△CAE△CBD,∴∠CAE=∠CBD.
(2)如图,过点C作CG∥AB,交AE的延长线于点G.
易得△ABE∽△GCE,∴,
又∵,∴,∴CG=CA,∴∠G=∠CAG,
∵AB∥CG,∴∠G=∠BAG,∴∠CAG=∠BAG.
∵∠CAE=∠CBD,∠AFD=∠BFE,∴∠ADF=∠BEF,∴△ADF∽△AEB,
∴,∴AB·AD=AF·AE.
11.解析(1)证明∵四边形ABCD是正方形,∴AD∥BC,且∠ABE=∠BAP=90°.
∴∠PAF=∠AEB,又∵PF⊥AE,∴∠PFA=∠ABE=90°,∴△PFA∽△ABE.
(2)①当△EFP∽△ABE时,∠PEF=∠EAB,∴PE∥AB,又AP∥BE,∠B=90°,
∴四边形ABEP为矩形,∴PA=EB=2,即x=2
②当△PFE∽△ABE时,∠PEF=∠AEB,
∵∠PAF=∠AEB,∴∠PEF=∠PAF,∴PE=PA∵PF⊥AE,∴F为AE的中点.
∵AE=,∴EF=AE=.
∵△PFE∽△ABE,∴,即,∴PE=5,
∴PA=5,即x=5.
综上所述,x的值为2或5.
_21?????????è?????(www.21cnjy.com)_
