变化率及导数(教案大赛一等奖)
图片预览


文档简介
§1.1.2导数的概念
教学目标:
知识与技能:通过具体实例,经历由平均变化率过渡到瞬时变化率的逼近过程,明确瞬时变化率即导数,从而形成导数概念.
过程与方法:⑴借助高台跳水问题,明确瞬时速度的含义;
⑵通过对瞬时速度的逼近过程,结合平均变化率,使学生认识到瞬时变化率的重大意义;
⑶结合其他实例,抽象出导数概念,使学生认识到导数就是瞬时变化率,了解导数的内涵.
情感、态度、价值观:通过运动的观点展现导数的内涵,使学生认识到“瞬时与永恒”的辨证关系,从而激发学生学习的兴趣.
教学重、难点:
重点:利用平均变化率的逼近瞬时变化率的过程及其理解;
难点:导数概念的形成,导数内涵的理解.
学法与教学用具:
教学方法:教师引导为主,学生自主探索、积极思考为辅;
教学手段:黑板和多媒体相结合,利用几何画板等数学工具演示逼近过程;
教学思想:以建构主义的“创设问题情境——提出数学问题——尝试解决问题——验证解题方法”为主,强调数学知识(导数概念)的建构过程;
教学用具:乒乓球(两枚)、几何画板课件、实物投影等.
教学设想:
教学基本情境 设计意图与评述 师生活动
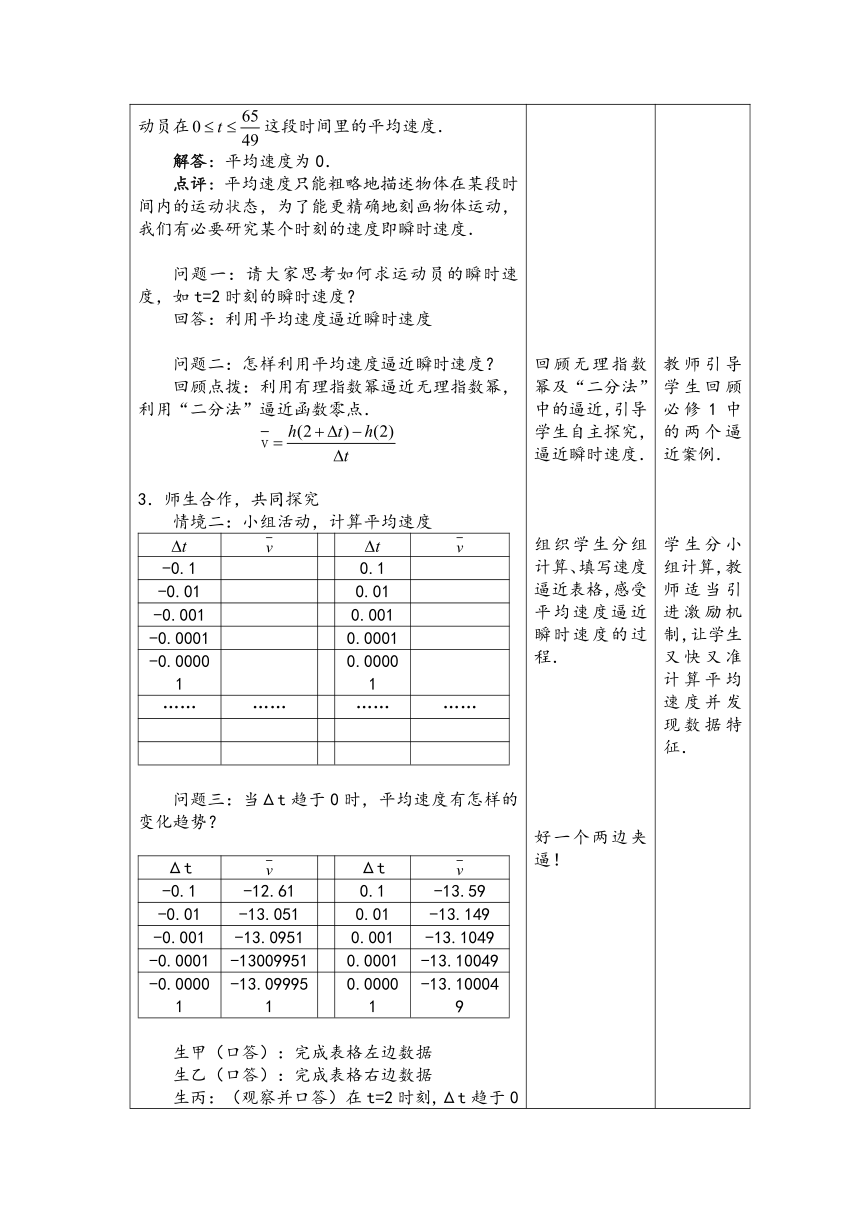
激趣激疑,引出课题情境一:教师手执两枚乒乓球,一枚拿稳、一枚抛动提问:两枚乒乓球是否相同?它们有何区别?回答:一枚是静止的,一枚是运动的T:但古希腊的大哲学家芝诺却不这么认为,他认为两枚乒乓球是一样的,因为在某个瞬间给它们拍照,它们的状态是一模一样的(在0时间里,位移为0).现代物理学告诉我们,这两枚乒乓球不一样,因为一个的瞬时速度为0,一个不为0.那怎样求一个物体的瞬时速度呢?引例分析,思想奠基引例1:在高台跳水运动中,运动员相对水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t) =-4.9t 2+6.5t+10.计算运动员在这段时间里的平均速度.解答:平均速度为0.点评:平均速度只能粗略地描述物体在某段时间内的运动状态,为了能更精确地刻画物体运动,我们有必要研究某个时刻的速度即瞬时速度.问题一:请大家思考如何求运动员的瞬时速度,如t=2时刻的瞬时速度?回答:利用平均速度逼近瞬时速度问题二:怎样利用平均速度逼近瞬时速度?回顾点拨:利用有理指数幂逼近无理指数幂,利用“二分法”逼近函数零点.师生合作,共同探究情境二:小组活动,计算平均速度-0.10.1-0.010.01-0.0010.001-0.00010.0001-0.000010.00001……………………问题三:当Δt趋于0时,平均速度有怎样的变化趋势?ΔtΔt-0.1-12.610.1-13.59-0.01-13.0510.01-13.149-0.001-13.09510.001-13.1049-0.0001-130099510.0001-13.10049-0.00001-13.0999510.00001-13.100049生甲(口答):完成表格左边数据生乙(口答):完成表格右边数据生丙:(观察并口答)在t=2时刻,Δt趋于0时,平均速度趋于一个确定的值-13.1,即瞬时速度.练习:求在t=1及1.5时刻,运动员的瞬时速度.解:;.问题四:运动员在某个时刻的瞬时速度如何表示呢?回答:.问题拓展,深化概念T:由上节课我们知道,速度是位移的变化率,那么瞬时速度就是位移的瞬时变化率,你能求出一般情况下的瞬时变化率吗?引例2:气球体积V(单位:L)与半径(单位:dm)之间的函数关系是当空气容量从增加到时,气球的平均膨胀率为你能写出气球在体积时的瞬时膨胀率吗?回答:.一般地,函数在处的瞬时变化率是我们称之为函数在处的导数,记作或,即.T:导数就是瞬时变化率,瞬时变化率是平均变化率的逼近.古希腊大哲学家芝诺无法理解这种逼近,他只知道瞬间可以堆积成永恒,殊不知永恒也可以通过逼近来表现瞬间,这就是唯物辨证论;人类用了几千年,直到17世纪的工业革命,人们才逐渐认识到这种逼近.一旦认识到这种逼近,我们才定义了导数的概念——导数是研究变化的一种强有力的工具!例题分析,练习巩固例1:将原油精炼为汽油、柴油、塑料等不同产品,需要对原油进行冷却和加热。如果在第x h时候,原油温度(单位:)为.计算第2h和第6h时,原油温度的瞬时变化率,并说明它的意义.解答:,;它说明在第2h附近,原油温度大约以3℃/h的速率下降;在第6h附近,原油问答大约以5℃/h的速率上升.练习:计算第3h和第5h时,原油温度的瞬时变化率,并说明它的意义.解答:,意义同上.点评:导数即瞬时变化率,可刻画物体变化的快慢.课堂小结,布置作业1°平均速度逼近瞬时速度2°瞬时变化率即导数的概念3°公式:课后练习:已知一个物体运动的位移(m)与时间t(s)满足关系S(t)=-2t2+5t⑴求物体第5秒和第6秒的瞬时速度⑵求物体在t时刻的瞬时速度⑶求物体t时刻运动的加速度,并判断物体作什么运动?作业(必做):P10,3、4作业(选做):P11,A组,5;P11,B组,1 利用芝诺“飞矢不动”悖论,吸引眼球,激发学生学习兴趣,并提出瞬时速度问题.通过具体问题,引导学生利用平均速度逼近瞬时速度.回顾无理指数幂及“二分法”中的逼近,引导学生自主探究,逼近瞬时速度.组织学生分组计算、填写速度逼近表格,感受平均速度逼近瞬时速度的过程.好一个两边夹逼!巩固逼近的思想方法,为后面的推广埋下伏笔!为瞬时变化率打下基础!速度是位移关于时间的变化率!从瞬时速度向瞬时变化率过渡!从特殊到一般,提出导数概念!承前起后,指出芝诺悖论的根源在于无法理解“瞬时与永恒”之间的辨证关系,升华学生的认识,并继续激发学习兴趣!巩固导数概念!导数的概念及其符号表示!作业体现层次性和选择性! 教师结合数学史实提出问题,引出课题.教师引导学生回顾必修1中的两个逼近案例.学生分小组计算,教师适当引进激励机制,让学生又快又准计算平均速度并发现数据特征.学生练习,教师纠错.类比、推广!学生接受导数符号,了解极限符号的意义!教师不失时机的进行数学文化渗透!学生练习!学生小结本节课所学内容!
板书设计§1.1.2导数的概念一、引例1二、逼近思想(无理指数幂与“二分法”)三、导数的概念四、归纳小结
评价设计本节课的教学安排是按照建构主义展开的,笔者力求让导数概念的生成符合螺旋上升特征!这尤其体现在本节课的例习题安排上,可以说适时的例习题演练是对学生学习情况最好反馈和评价.引例1的前三个问题,一环扣一环,力求让学生理解瞬时速度、理解逼近过程;问题三后的练习就是针对这种学习情况的评价,教师以此检阅学生对逼近过程的理解程度,要求学生至少在形式上知道这种逼近方法(实质是取极限).引例2是对引例1的推广,也就是将瞬时速度推广到瞬时变化率,这是本节课的第二次思维提升;例1及后面的练习则是在给出导数概念后,进一步巩固所学知识.课后练习是对本节课的又一次小结,教师通过习题揭示导数的内涵;必做的作业是对导数概念的基本要求,选做的作业则提出更高的要求,为后面的几何意义及进一步推广埋下伏笔!
课后反思:
从旧教材上看,导数概念学习的起点是极限,即从数列的极限,到函数的极限,再到导数。这种概念建立方式具有严密的逻辑性和系统性,但学生很难理解极限的形式化定义,因此也影响了对导数本质的理解。
新教材不介绍极限的形式化定义及相关知识,而是用直观形象的逼近方法定义导数。通过列表计算、直观地把握函数变化趋势(蕴涵着极限的描述性定义),学生更易于理解。
这堂课由平均速度到瞬时速度再到导数,展示了一个完整的数学探究过程。提出问题、计算观察、发现规律、给出定义,让学生经历了知识再发现的过程,促进了个性化学习。
在教学中尝试采用创设问题情景,以问题驱动、层层铺垫,帮助学生实现从被动接受知识变为主动获取知识;同时也试图改进学生的学习方式,以小组合作的方式展开,在合作中相互配合。灵活融合引导启发、数形结合、激励评价、多媒体辅助等教学方式,更好地实现教学目标。
在教学过程中,不失时机的进行数学文化渗透,除了能激发学生的学习兴趣、增强学习信心外,更是体现出了数学探索原貌,让学生看到数学探索的艰难和有趣,更客观的认识导数及发明导数的现实意义,这对接受和理解导数这个概念大有裨益!
本节课内容较多,一课时难以完成,教师可以根据教学实际删减该课例中的某些环节,比如后面的例1及练习题等!
电脑投影屏幕
列表(实物投影)
课后练习
作业:
教学目标:
知识与技能:通过具体实例,经历由平均变化率过渡到瞬时变化率的逼近过程,明确瞬时变化率即导数,从而形成导数概念.
过程与方法:⑴借助高台跳水问题,明确瞬时速度的含义;
⑵通过对瞬时速度的逼近过程,结合平均变化率,使学生认识到瞬时变化率的重大意义;
⑶结合其他实例,抽象出导数概念,使学生认识到导数就是瞬时变化率,了解导数的内涵.
情感、态度、价值观:通过运动的观点展现导数的内涵,使学生认识到“瞬时与永恒”的辨证关系,从而激发学生学习的兴趣.
教学重、难点:
重点:利用平均变化率的逼近瞬时变化率的过程及其理解;
难点:导数概念的形成,导数内涵的理解.
学法与教学用具:
教学方法:教师引导为主,学生自主探索、积极思考为辅;
教学手段:黑板和多媒体相结合,利用几何画板等数学工具演示逼近过程;
教学思想:以建构主义的“创设问题情境——提出数学问题——尝试解决问题——验证解题方法”为主,强调数学知识(导数概念)的建构过程;
教学用具:乒乓球(两枚)、几何画板课件、实物投影等.
教学设想:
教学基本情境 设计意图与评述 师生活动
激趣激疑,引出课题情境一:教师手执两枚乒乓球,一枚拿稳、一枚抛动提问:两枚乒乓球是否相同?它们有何区别?回答:一枚是静止的,一枚是运动的T:但古希腊的大哲学家芝诺却不这么认为,他认为两枚乒乓球是一样的,因为在某个瞬间给它们拍照,它们的状态是一模一样的(在0时间里,位移为0).现代物理学告诉我们,这两枚乒乓球不一样,因为一个的瞬时速度为0,一个不为0.那怎样求一个物体的瞬时速度呢?引例分析,思想奠基引例1:在高台跳水运动中,运动员相对水面的高度h(单位:m)与起跳后的时间t(单位:s)存在函数关系h(t) =-4.9t 2+6.5t+10.计算运动员在这段时间里的平均速度.解答:平均速度为0.点评:平均速度只能粗略地描述物体在某段时间内的运动状态,为了能更精确地刻画物体运动,我们有必要研究某个时刻的速度即瞬时速度.问题一:请大家思考如何求运动员的瞬时速度,如t=2时刻的瞬时速度?回答:利用平均速度逼近瞬时速度问题二:怎样利用平均速度逼近瞬时速度?回顾点拨:利用有理指数幂逼近无理指数幂,利用“二分法”逼近函数零点.师生合作,共同探究情境二:小组活动,计算平均速度-0.10.1-0.010.01-0.0010.001-0.00010.0001-0.000010.00001……………………问题三:当Δt趋于0时,平均速度有怎样的变化趋势?ΔtΔt-0.1-12.610.1-13.59-0.01-13.0510.01-13.149-0.001-13.09510.001-13.1049-0.0001-130099510.0001-13.10049-0.00001-13.0999510.00001-13.100049生甲(口答):完成表格左边数据生乙(口答):完成表格右边数据生丙:(观察并口答)在t=2时刻,Δt趋于0时,平均速度趋于一个确定的值-13.1,即瞬时速度.练习:求在t=1及1.5时刻,运动员的瞬时速度.解:;.问题四:运动员在某个时刻的瞬时速度如何表示呢?回答:.问题拓展,深化概念T:由上节课我们知道,速度是位移的变化率,那么瞬时速度就是位移的瞬时变化率,你能求出一般情况下的瞬时变化率吗?引例2:气球体积V(单位:L)与半径(单位:dm)之间的函数关系是当空气容量从增加到时,气球的平均膨胀率为你能写出气球在体积时的瞬时膨胀率吗?回答:.一般地,函数在处的瞬时变化率是我们称之为函数在处的导数,记作或,即.T:导数就是瞬时变化率,瞬时变化率是平均变化率的逼近.古希腊大哲学家芝诺无法理解这种逼近,他只知道瞬间可以堆积成永恒,殊不知永恒也可以通过逼近来表现瞬间,这就是唯物辨证论;人类用了几千年,直到17世纪的工业革命,人们才逐渐认识到这种逼近.一旦认识到这种逼近,我们才定义了导数的概念——导数是研究变化的一种强有力的工具!例题分析,练习巩固例1:将原油精炼为汽油、柴油、塑料等不同产品,需要对原油进行冷却和加热。如果在第x h时候,原油温度(单位:)为.计算第2h和第6h时,原油温度的瞬时变化率,并说明它的意义.解答:,;它说明在第2h附近,原油温度大约以3℃/h的速率下降;在第6h附近,原油问答大约以5℃/h的速率上升.练习:计算第3h和第5h时,原油温度的瞬时变化率,并说明它的意义.解答:,意义同上.点评:导数即瞬时变化率,可刻画物体变化的快慢.课堂小结,布置作业1°平均速度逼近瞬时速度2°瞬时变化率即导数的概念3°公式:课后练习:已知一个物体运动的位移(m)与时间t(s)满足关系S(t)=-2t2+5t⑴求物体第5秒和第6秒的瞬时速度⑵求物体在t时刻的瞬时速度⑶求物体t时刻运动的加速度,并判断物体作什么运动?作业(必做):P10,3、4作业(选做):P11,A组,5;P11,B组,1 利用芝诺“飞矢不动”悖论,吸引眼球,激发学生学习兴趣,并提出瞬时速度问题.通过具体问题,引导学生利用平均速度逼近瞬时速度.回顾无理指数幂及“二分法”中的逼近,引导学生自主探究,逼近瞬时速度.组织学生分组计算、填写速度逼近表格,感受平均速度逼近瞬时速度的过程.好一个两边夹逼!巩固逼近的思想方法,为后面的推广埋下伏笔!为瞬时变化率打下基础!速度是位移关于时间的变化率!从瞬时速度向瞬时变化率过渡!从特殊到一般,提出导数概念!承前起后,指出芝诺悖论的根源在于无法理解“瞬时与永恒”之间的辨证关系,升华学生的认识,并继续激发学习兴趣!巩固导数概念!导数的概念及其符号表示!作业体现层次性和选择性! 教师结合数学史实提出问题,引出课题.教师引导学生回顾必修1中的两个逼近案例.学生分小组计算,教师适当引进激励机制,让学生又快又准计算平均速度并发现数据特征.学生练习,教师纠错.类比、推广!学生接受导数符号,了解极限符号的意义!教师不失时机的进行数学文化渗透!学生练习!学生小结本节课所学内容!
板书设计§1.1.2导数的概念一、引例1二、逼近思想(无理指数幂与“二分法”)三、导数的概念四、归纳小结
评价设计本节课的教学安排是按照建构主义展开的,笔者力求让导数概念的生成符合螺旋上升特征!这尤其体现在本节课的例习题安排上,可以说适时的例习题演练是对学生学习情况最好反馈和评价.引例1的前三个问题,一环扣一环,力求让学生理解瞬时速度、理解逼近过程;问题三后的练习就是针对这种学习情况的评价,教师以此检阅学生对逼近过程的理解程度,要求学生至少在形式上知道这种逼近方法(实质是取极限).引例2是对引例1的推广,也就是将瞬时速度推广到瞬时变化率,这是本节课的第二次思维提升;例1及后面的练习则是在给出导数概念后,进一步巩固所学知识.课后练习是对本节课的又一次小结,教师通过习题揭示导数的内涵;必做的作业是对导数概念的基本要求,选做的作业则提出更高的要求,为后面的几何意义及进一步推广埋下伏笔!
课后反思:
从旧教材上看,导数概念学习的起点是极限,即从数列的极限,到函数的极限,再到导数。这种概念建立方式具有严密的逻辑性和系统性,但学生很难理解极限的形式化定义,因此也影响了对导数本质的理解。
新教材不介绍极限的形式化定义及相关知识,而是用直观形象的逼近方法定义导数。通过列表计算、直观地把握函数变化趋势(蕴涵着极限的描述性定义),学生更易于理解。
这堂课由平均速度到瞬时速度再到导数,展示了一个完整的数学探究过程。提出问题、计算观察、发现规律、给出定义,让学生经历了知识再发现的过程,促进了个性化学习。
在教学中尝试采用创设问题情景,以问题驱动、层层铺垫,帮助学生实现从被动接受知识变为主动获取知识;同时也试图改进学生的学习方式,以小组合作的方式展开,在合作中相互配合。灵活融合引导启发、数形结合、激励评价、多媒体辅助等教学方式,更好地实现教学目标。
在教学过程中,不失时机的进行数学文化渗透,除了能激发学生的学习兴趣、增强学习信心外,更是体现出了数学探索原貌,让学生看到数学探索的艰难和有趣,更客观的认识导数及发明导数的现实意义,这对接受和理解导数这个概念大有裨益!
本节课内容较多,一课时难以完成,教师可以根据教学实际删减该课例中的某些环节,比如后面的例1及练习题等!
电脑投影屏幕
列表(实物投影)
课后练习
作业:
