苏科版数学八年级上 【课题】§3.5矩形、菱形、正方形(4和5)
文档属性
| 名称 | 苏科版数学八年级上 【课题】§3.5矩形、菱形、正方形(4和5) |  | |
| 格式 | zip | ||
| 文件大小 | 24.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-28 19:05:09 | ||
图片预览


文档简介
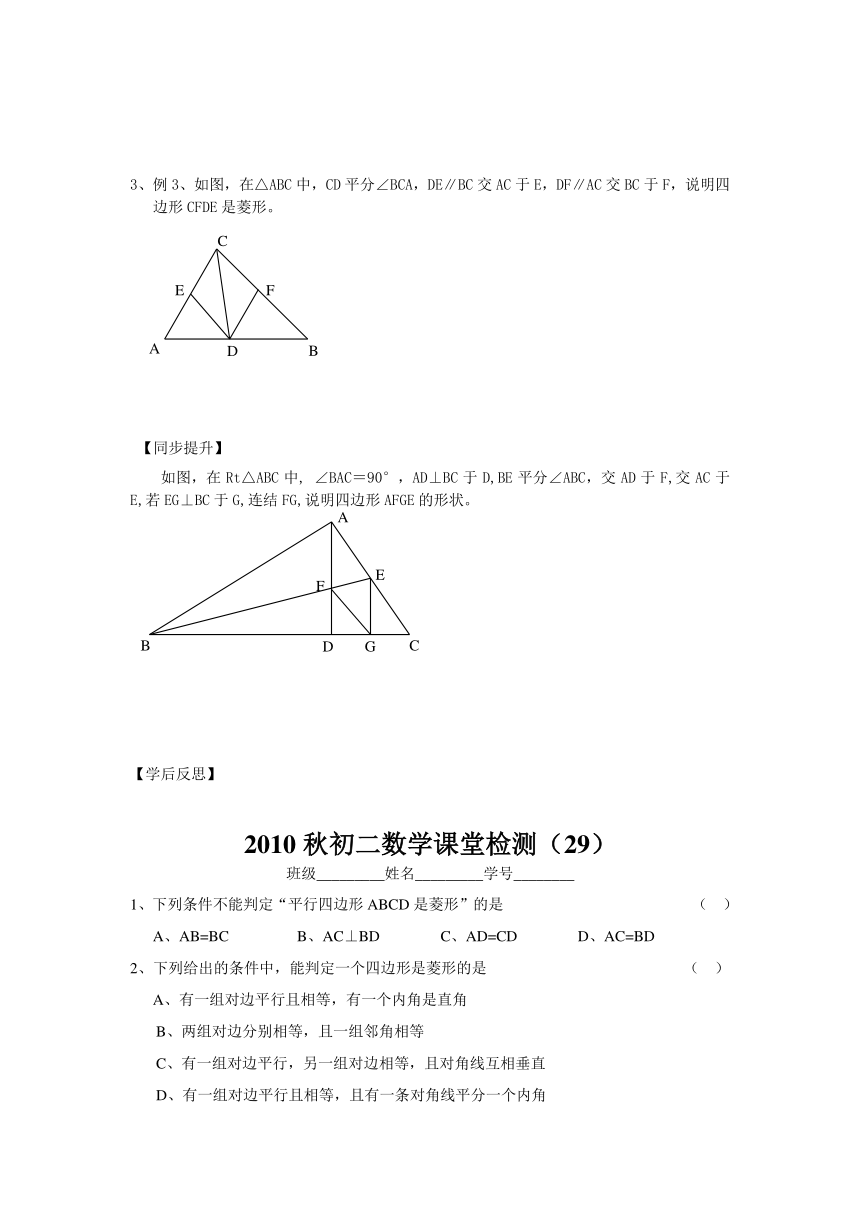
2010年秋初二数学导学案
【课题】§3.5矩形、菱形、正方形(4)
【学习目标】1、掌握四边形是菱形的条件,进一步获得判定菱形的方法,积累经验,形成解决问题的能力;
2、经历菱形的判定方法的探索过程,在活动中,发展合情推理意识,和主动探究的习惯,初步掌握说理的基本方法,发展有条理的表达能力;
【引入导学】
1、菱形是特殊的平行四边形,你能说一说特殊在什么地方?
2、菱形是特殊的平行四边形,它具有平行四边形一切性质,还具有一般平行四边形没有的特殊性质,你能把菱形的特殊性质写出来吗?
3、将2张宽相等的矩形纸片合在一起,得到四边形ABCD如图,你认为它是什么特殊的平行四边形?请动手叠一叠,检验你的猜想。
4、在平行四边形ABCD中,AC⊥BD,垂足为O,平行四边形ABCD是菱形吗?为什么?
【小组交流】
一个四边形是菱形的条件:
(1)邻边 的平行四边形是菱形。
(2)对角线 的平行四边形是菱形。
(3) 的四边形是菱形。
【学生展示】
1、例1、在四边形ABCD中,对角线AC与BD相交于点O,OC=OA,OB=OD且 AC⊥BD,请你说明四边形ABCD是菱形。
2、例2、在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F,四边形AFCE是菱形吗?说说你的理由.
3、例3、如图,在△ABC中,CD平分∠BCA,DE∥BC交AC于E,DF∥AC交BC于F,说明四边形CFDE是菱形。
【同步提升】
如图,在Rt△ABC中, ∠BAC=90°,AD⊥BC于D,BE平分∠ABC,交AD于F,交AC于E,若EG⊥BC于G,连结FG,说明四边形AFGE的形状。
【学后反思】
2010秋初二数学课堂检测(29)
班级_________姓名_________学号________
1、下列条件不能判定“平行四边形ABCD是菱形”的是 ( )
A、AB=BC B、AC⊥BD C、AD=CD D、AC=BD
2、下列给出的条件中,能判定一个四边形是菱形的是 ( )
A、有一组对边平行且相等,有一个内角是直角
B、两组对边分别相等,且一组邻角相等
C、有一组对边平行,另一组对边相等,且对角线互相垂直
D、有一组对边平行且相等,且有一条对角线平分一个内角
3、下列判断正确的是 ( )
A、两邻边相等的四边形是菱形
B、一条对角线平分一个内角的平行四边形是菱形
C、对角线互相垂直的四边形是菱形
D、对角线互相垂直且有一组邻边相等的四边形是菱形
4、□ABCD的对角线AC、BD相交于点O,分别添加下列条件:①AC⊥BD ②AB=BC ③AC平分∠BAD ④AO=DO,能使□ABCD是菱形的条件有 ( )
A、1个 B、2个 C、3个 D、4个
5、已知:如图,在△ABC中,AD是∠BAC的平分线,EF是AD的垂直平分线,分别交AB于E,交AC于F,那么四边形AEDF是菱形吗?为什么?
2010年秋初二数学导学案(30)
【课题】§3·6正方形(1)
【学习目标】经历探索正方形的性质和判别条件的过程,在操作活动和观察、分析过程中发展学生的主动探究习惯,进一步了解和体会说理的基本方法
【引入导学】
(1)你能用矩形纸片折出1个正方形吗?用虚线画出
折叠线。
(2)你能把一个菱形木框变成正方形木框?动手
试一试,并画出用虚线画出变化的过程图形和用
文字说明变动的方法。
(3)如图,BO是等腰直角三角形ABC的底边AC上的中线,
画出△ABC关于点O对称的图形;把点B关于点O的对
称点记为D,连结DA、DC想一想,四边形ABCD有什么特点?
【小组交流】
1、正方形的概念:
________________________________________叫做正方形。
2、正方形的性质:
(1)对称性:________________________________________;
(2)边:____________________________________________;
(3)角:____________________________________________;
(4)对角线:________________________________________。
3、正方形与平行四边形,矩形与菱形的关系:
把名称填入相应的图开形内
【学生展示】
1、例1:正方形ABCD的两条对角线AC和BD相交于点O,
△AOB、△BOC、△COD、△AOD是什么样的三角形?
他们之间有什么关系?并说明理由。
2、例2:如图,已知正方形ABCD,延长AB到E,
作AG⊥EC于G,AG交BC于F,说明:AF=CE。
3、例3、正方形ABCD中,点E是对角线AC上的
任意一点,连结BE、DE,则BE与DE大小关系
如何?并说明理由。
4、例4、如图,四边形ABCD是正方形,点E是AC上的点EG⊥BC,EF⊥AB,(1)试猜测DE与FG关系如何?并说明理由。(2)如果正方形ABCD的边长为4㎝,求四边形BGEF的周长
【能力提升】
如图,在△ABC中,∠C=900,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F。(1)问四边形CFDE是正方形吗?请说明理由;(2)若AC=3,BC=4,则CF的长为多少?
【学后反思】
2010年秋初二数学课堂检测(30)
班级_________姓名_________学号________
1、正方形、矩形、菱形都具有的特征是月日 ( )
A、对角线互相平分 B、对角线相等
C、对角线互相垂直 D、对角线平分一组对角
2、下列结论:
(1)正方形具有平行四边形的一切性质;
(2)正方形具有矩形的一切性质;
(3)正方形具有菱形的一切性质;
(4)正方形具有四边形的一切性质,其中正确结论有 ( )
A、1个 B、2个 C、3个 D、4个
3、正方形的边长为a,当边长增加1时,其面积增加了 。
4、如图,点E是正方形ABCD的边BC延长线上的一点,且CE=AC,若AE交CD于点F,则∠E= °;∠AFC=
5、如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于E,
交CD于F,则∠BEC= 度.
6、如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由。
A
B
D
C
A
D
C
B
O
A
D
C
B
O
A
B
F
C
E
D
A
B
C
E
G
D
F
A
F
E
D
B
C
A
D
C
B
B
A
C
O
O
D
A
B
C
A
D
C
E
B
F
G
D
A
B
C
E
D
A
B
C
E
F
G
A
F
C
E
D
B
A
B
C
E
F
D
_
F
_
E
_
D
_
C
_
B
_
A
D
C
O
M
N
B
A
【课题】§3.5矩形、菱形、正方形(4)
【学习目标】1、掌握四边形是菱形的条件,进一步获得判定菱形的方法,积累经验,形成解决问题的能力;
2、经历菱形的判定方法的探索过程,在活动中,发展合情推理意识,和主动探究的习惯,初步掌握说理的基本方法,发展有条理的表达能力;
【引入导学】
1、菱形是特殊的平行四边形,你能说一说特殊在什么地方?
2、菱形是特殊的平行四边形,它具有平行四边形一切性质,还具有一般平行四边形没有的特殊性质,你能把菱形的特殊性质写出来吗?
3、将2张宽相等的矩形纸片合在一起,得到四边形ABCD如图,你认为它是什么特殊的平行四边形?请动手叠一叠,检验你的猜想。
4、在平行四边形ABCD中,AC⊥BD,垂足为O,平行四边形ABCD是菱形吗?为什么?
【小组交流】
一个四边形是菱形的条件:
(1)邻边 的平行四边形是菱形。
(2)对角线 的平行四边形是菱形。
(3) 的四边形是菱形。
【学生展示】
1、例1、在四边形ABCD中,对角线AC与BD相交于点O,OC=OA,OB=OD且 AC⊥BD,请你说明四边形ABCD是菱形。
2、例2、在四边形ABCD中,AD∥BC,对角线AC的垂直平分线与边AD、BC分别相交于点E、F,四边形AFCE是菱形吗?说说你的理由.
3、例3、如图,在△ABC中,CD平分∠BCA,DE∥BC交AC于E,DF∥AC交BC于F,说明四边形CFDE是菱形。
【同步提升】
如图,在Rt△ABC中, ∠BAC=90°,AD⊥BC于D,BE平分∠ABC,交AD于F,交AC于E,若EG⊥BC于G,连结FG,说明四边形AFGE的形状。
【学后反思】
2010秋初二数学课堂检测(29)
班级_________姓名_________学号________
1、下列条件不能判定“平行四边形ABCD是菱形”的是 ( )
A、AB=BC B、AC⊥BD C、AD=CD D、AC=BD
2、下列给出的条件中,能判定一个四边形是菱形的是 ( )
A、有一组对边平行且相等,有一个内角是直角
B、两组对边分别相等,且一组邻角相等
C、有一组对边平行,另一组对边相等,且对角线互相垂直
D、有一组对边平行且相等,且有一条对角线平分一个内角
3、下列判断正确的是 ( )
A、两邻边相等的四边形是菱形
B、一条对角线平分一个内角的平行四边形是菱形
C、对角线互相垂直的四边形是菱形
D、对角线互相垂直且有一组邻边相等的四边形是菱形
4、□ABCD的对角线AC、BD相交于点O,分别添加下列条件:①AC⊥BD ②AB=BC ③AC平分∠BAD ④AO=DO,能使□ABCD是菱形的条件有 ( )
A、1个 B、2个 C、3个 D、4个
5、已知:如图,在△ABC中,AD是∠BAC的平分线,EF是AD的垂直平分线,分别交AB于E,交AC于F,那么四边形AEDF是菱形吗?为什么?
2010年秋初二数学导学案(30)
【课题】§3·6正方形(1)
【学习目标】经历探索正方形的性质和判别条件的过程,在操作活动和观察、分析过程中发展学生的主动探究习惯,进一步了解和体会说理的基本方法
【引入导学】
(1)你能用矩形纸片折出1个正方形吗?用虚线画出
折叠线。
(2)你能把一个菱形木框变成正方形木框?动手
试一试,并画出用虚线画出变化的过程图形和用
文字说明变动的方法。
(3)如图,BO是等腰直角三角形ABC的底边AC上的中线,
画出△ABC关于点O对称的图形;把点B关于点O的对
称点记为D,连结DA、DC想一想,四边形ABCD有什么特点?
【小组交流】
1、正方形的概念:
________________________________________叫做正方形。
2、正方形的性质:
(1)对称性:________________________________________;
(2)边:____________________________________________;
(3)角:____________________________________________;
(4)对角线:________________________________________。
3、正方形与平行四边形,矩形与菱形的关系:
把名称填入相应的图开形内
【学生展示】
1、例1:正方形ABCD的两条对角线AC和BD相交于点O,
△AOB、△BOC、△COD、△AOD是什么样的三角形?
他们之间有什么关系?并说明理由。
2、例2:如图,已知正方形ABCD,延长AB到E,
作AG⊥EC于G,AG交BC于F,说明:AF=CE。
3、例3、正方形ABCD中,点E是对角线AC上的
任意一点,连结BE、DE,则BE与DE大小关系
如何?并说明理由。
4、例4、如图,四边形ABCD是正方形,点E是AC上的点EG⊥BC,EF⊥AB,(1)试猜测DE与FG关系如何?并说明理由。(2)如果正方形ABCD的边长为4㎝,求四边形BGEF的周长
【能力提升】
如图,在△ABC中,∠C=900,∠BAC、∠ABC的角平分线交于点D,DE⊥BC于E,DF⊥AC于F。(1)问四边形CFDE是正方形吗?请说明理由;(2)若AC=3,BC=4,则CF的长为多少?
【学后反思】
2010年秋初二数学课堂检测(30)
班级_________姓名_________学号________
1、正方形、矩形、菱形都具有的特征是月日 ( )
A、对角线互相平分 B、对角线相等
C、对角线互相垂直 D、对角线平分一组对角
2、下列结论:
(1)正方形具有平行四边形的一切性质;
(2)正方形具有矩形的一切性质;
(3)正方形具有菱形的一切性质;
(4)正方形具有四边形的一切性质,其中正确结论有 ( )
A、1个 B、2个 C、3个 D、4个
3、正方形的边长为a,当边长增加1时,其面积增加了 。
4、如图,点E是正方形ABCD的边BC延长线上的一点,且CE=AC,若AE交CD于点F,则∠E= °;∠AFC=
5、如图,正方形ABCD中,∠DAF=25°,AF交对角线BD于E,
交CD于F,则∠BEC= 度.
6、如图,在正方形ABCD的边BC上任取一点M,过点C作CN⊥DM交AB于N,设正方形对角线交点为O,试确定OM与ON之间的关系,并说明理由。
A
B
D
C
A
D
C
B
O
A
D
C
B
O
A
B
F
C
E
D
A
B
C
E
G
D
F
A
F
E
D
B
C
A
D
C
B
B
A
C
O
O
D
A
B
C
A
D
C
E
B
F
G
D
A
B
C
E
D
A
B
C
E
F
G
A
F
C
E
D
B
A
B
C
E
F
D
_
F
_
E
_
D
_
C
_
B
_
A
D
C
O
M
N
B
A
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
