七年级数学有理数的乘法法则 课件
文档属性
| 名称 | 七年级数学有理数的乘法法则 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 309.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-28 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
知之者不如好之者,好知者不如乐知者。
——孔子
进入
有理数的乘法法则
问题的提出
试试你自己
有理数的乘法法则
例题展示
课堂练习
课堂小结
小资料
问题的提出
一只小虫,沿一条东西巷的跑道,以每分钟3米的速度向东爬行2分钟,那么它现在位于原来位置的哪个方向?相距多少米?
说明:若规定向东为正,向西为负
我的解释:
这个问题用乘法来解答为:
3×2=6
即小虫位于原来位置的东方6米处
能用数轴表示这一事实么?动手画一画吧。
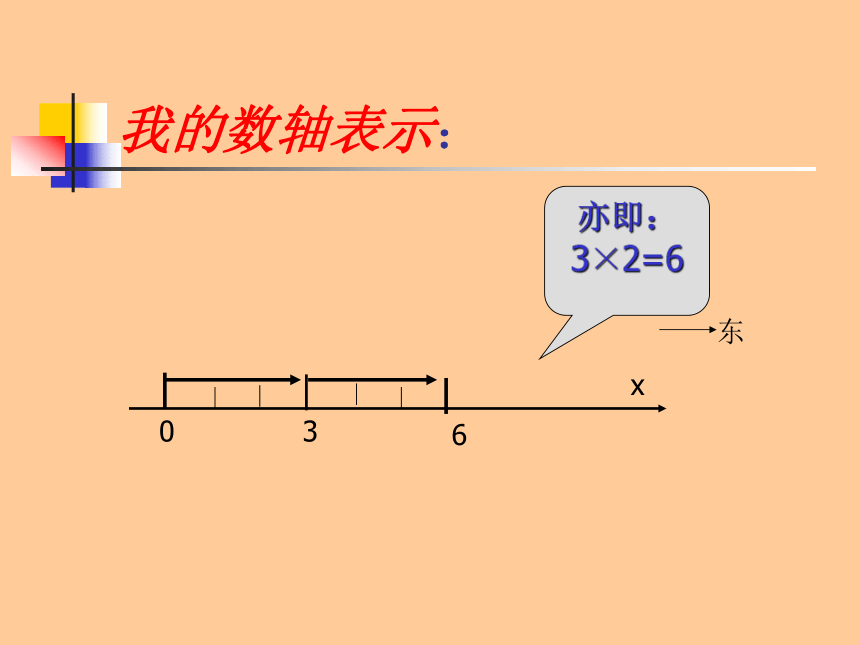
我的数轴表示:
0
3
6
x
东
亦即:3×2=6
问题提出2
一只小虫,沿一条东西巷的跑道,以每分钟3米的速度向西爬行2分钟,那么它现在位于原来位置的哪个方向?相距多少米?
请你也用算式和数轴的方式予以解答
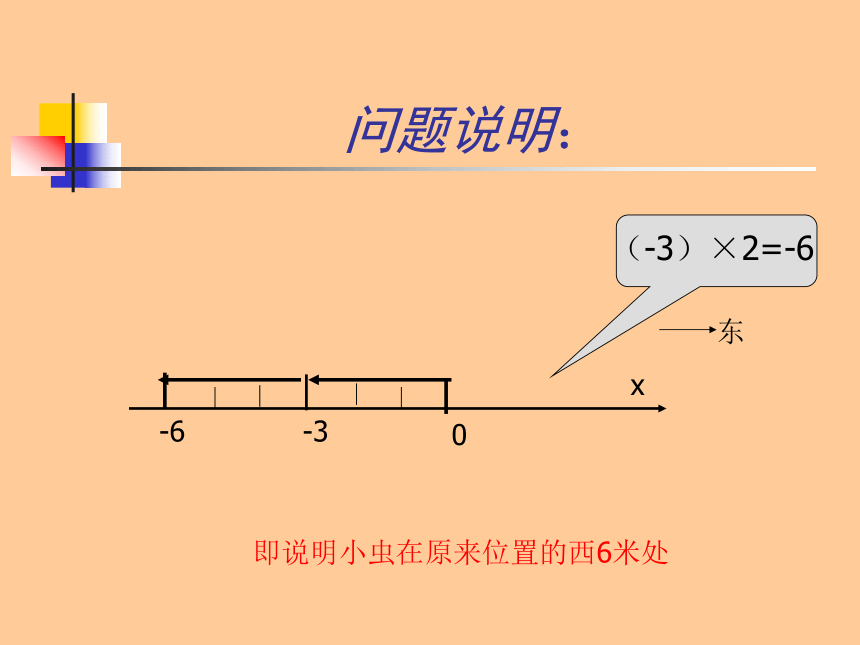
问题说明:
-6
-3
0
x
东
(-3)×2=-6
即说明小虫在原来位置的西6米处
比较以上的两个算式,你有什么发现?
(-3)×2=-6
3×2=6
从以上的实例可以看出,当我们把两个正数乘积中的一个因数换成它的相反数时,其乘积的结果也变成了原来的相反数。
一般的,把一个因数换成它的相反数,所得的积是原来积的相反数。
回主页
试试你自己
(-5)×2=
3×(-4)=
-6
-10
-12
3×(-2)=
一般的,把一个因数换成它的相反数,所得的积是原来积的相反数。
回主页
有理数的乘法法则:
前面我们知道了两个因数相乘时,改变其中的一个因数的符号后,乘积的符号也发生了改变。请看下面的运算,你能解释么?
(-3)×(-2)=6
(-3)×2我们知道它的乘积是-6,当我们把因数2变成其相反数(-2)时,由刚才的道理(规则)可知,其乘积也应当变为原来乘积的相反数。
3×2=6
(-3)×2=-6
(-5)×2=-10
3×(-4)=-12
(-3)×(-2)=6
从以上的练习等都在表明两数相乘之间的某种规律,你能说说么?特殊情况你考虑了么?
得出有理数乘法法则:
我们可以从两数的符号变化来探究积的符号变化,并决定乘得的最后数值结果。
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0。
我的解释
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-5)×(-2)
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-5)×(-2)=+( )的判断
三,把绝对值相乘,得出结果。
所以有
(-5)×(-2)=+(10)的结果
感受法则、理解法则:
再例如计算(-6)×4
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-6)×4= -( )的判断
三,把绝对值相乘,得出结果。
所以有
(-6)×4= -(24)的结果
感受法则、理解法则
若均用 或 表示是相同符号的
数相乘的话,请判断下面几种图形相乘所得到的图形结果。
+
-
+
-
×
=
+
+
+
-
-
-
×
×
×
=
=
=
-
+
-
+
回主页
例题学习
计算:
①(-5)×(-6); ②
解: (-5)×(-6)
解:
=+( 5×6)
=30
回主页
课堂练习
请解答教材P52中的练习1、2、3。
书中的想一想的问题,你想好了么?请你来回答行么?
任何数同1相乘,结果仍得原数;任何数同(-1)相乘,得原数的相反数。
课堂练习(正误辨析)
你能看出下面计算有误么?
计算:
解:原式=
=
这个解答正确么?你认为应该怎么做?答案是多少呢?
课堂练习(选择题)
1)如果a×b=0,则这两个数 ( )
A 都等于0, B 有一个等于0,另一个不等于0;
C 至少有一个等于0, D 互为相反数
2)已知-3a是一个负数,则 ( )
A a>0 B a<0 C a≥0 D a≤0
C
A
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
回主页
课堂小结
1)有理数的乘法法则,它的做法带给我们这样的启示。
2)特殊的乘法运算,比如任何数同0相乘,任何数同1或者(-1)相乘,互为倒数的两个数相乘等等。
3)我们在进行乘法运算的时候,应该注意些什么呢?
回主页
读一读 数字成语算式
(三天打渔)- (两天晒网)=(一事无成)
3 - 2 = 1
(十年树木) × (百年树人)=(各有千秋)
10 × 100 = 1000
(三顾茅庐) + (三十六计)=(五湖四海)
3 + 6 = 9
成语与算式
(五颜六色) ÷(七窍生烟)=(八面玲珑)
56 ÷ 7 = 8
(一问三不知) × (六神无主)=(七荤八素)
13 × 6 = 78
回主页
知之者不如好之者,好知者不如乐知者。
——孔子
进入
有理数的乘法法则
问题的提出
试试你自己
有理数的乘法法则
例题展示
课堂练习
课堂小结
小资料
问题的提出
一只小虫,沿一条东西巷的跑道,以每分钟3米的速度向东爬行2分钟,那么它现在位于原来位置的哪个方向?相距多少米?
说明:若规定向东为正,向西为负
我的解释:
这个问题用乘法来解答为:
3×2=6
即小虫位于原来位置的东方6米处
能用数轴表示这一事实么?动手画一画吧。
我的数轴表示:
0
3
6
x
东
亦即:3×2=6
问题提出2
一只小虫,沿一条东西巷的跑道,以每分钟3米的速度向西爬行2分钟,那么它现在位于原来位置的哪个方向?相距多少米?
请你也用算式和数轴的方式予以解答
问题说明:
-6
-3
0
x
东
(-3)×2=-6
即说明小虫在原来位置的西6米处
比较以上的两个算式,你有什么发现?
(-3)×2=-6
3×2=6
从以上的实例可以看出,当我们把两个正数乘积中的一个因数换成它的相反数时,其乘积的结果也变成了原来的相反数。
一般的,把一个因数换成它的相反数,所得的积是原来积的相反数。
回主页
试试你自己
(-5)×2=
3×(-4)=
-6
-10
-12
3×(-2)=
一般的,把一个因数换成它的相反数,所得的积是原来积的相反数。
回主页
有理数的乘法法则:
前面我们知道了两个因数相乘时,改变其中的一个因数的符号后,乘积的符号也发生了改变。请看下面的运算,你能解释么?
(-3)×(-2)=6
(-3)×2我们知道它的乘积是-6,当我们把因数2变成其相反数(-2)时,由刚才的道理(规则)可知,其乘积也应当变为原来乘积的相反数。
3×2=6
(-3)×2=-6
(-5)×2=-10
3×(-4)=-12
(-3)×(-2)=6
从以上的练习等都在表明两数相乘之间的某种规律,你能说说么?特殊情况你考虑了么?
得出有理数乘法法则:
我们可以从两数的符号变化来探究积的符号变化,并决定乘得的最后数值结果。
有理数乘法法则:
两数相乘,同号得正,异号得负,并把绝对值相乘;
任何数同0相乘,都得0。
我的解释
感受法则、理解法则:
有理数乘法法则也秉承了有理数加减的探究思路,即将问题予以归类处理,分类计算,这样有助于我们问题的解决。
例如计算(-5)×(-2)
一,是同号相乘,所乘得的结果应为正。
二,可以先得到(-5)×(-2)=+( )的判断
三,把绝对值相乘,得出结果。
所以有
(-5)×(-2)=+(10)的结果
感受法则、理解法则:
再例如计算(-6)×4
一,是异号相乘,所乘得的结果应为负。
二,可以先得到(-6)×4= -( )的判断
三,把绝对值相乘,得出结果。
所以有
(-6)×4= -(24)的结果
感受法则、理解法则
若均用 或 表示是相同符号的
数相乘的话,请判断下面几种图形相乘所得到的图形结果。
+
-
+
-
×
=
+
+
+
-
-
-
×
×
×
=
=
=
-
+
-
+
回主页
例题学习
计算:
①(-5)×(-6); ②
解: (-5)×(-6)
解:
=+( 5×6)
=30
回主页
课堂练习
请解答教材P52中的练习1、2、3。
书中的想一想的问题,你想好了么?请你来回答行么?
任何数同1相乘,结果仍得原数;任何数同(-1)相乘,得原数的相反数。
课堂练习(正误辨析)
你能看出下面计算有误么?
计算:
解:原式=
=
这个解答正确么?你认为应该怎么做?答案是多少呢?
课堂练习(选择题)
1)如果a×b=0,则这两个数 ( )
A 都等于0, B 有一个等于0,另一个不等于0;
C 至少有一个等于0, D 互为相反数
2)已知-3a是一个负数,则 ( )
A a>0 B a<0 C a≥0 D a≤0
C
A
课堂练习
3)两个有理数和为0,积为负,则这两个数的关系是 ( )
A 两个数均为0, B 两个数中一个为0
C 两数互为相反数, D 两数互为相反数,但不为0。
D
回主页
课堂小结
1)有理数的乘法法则,它的做法带给我们这样的启示。
2)特殊的乘法运算,比如任何数同0相乘,任何数同1或者(-1)相乘,互为倒数的两个数相乘等等。
3)我们在进行乘法运算的时候,应该注意些什么呢?
回主页
读一读 数字成语算式
(三天打渔)- (两天晒网)=(一事无成)
3 - 2 = 1
(十年树木) × (百年树人)=(各有千秋)
10 × 100 = 1000
(三顾茅庐) + (三十六计)=(五湖四海)
3 + 6 = 9
成语与算式
(五颜六色) ÷(七窍生烟)=(八面玲珑)
56 ÷ 7 = 8
(一问三不知) × (六神无主)=(七荤八素)
13 × 6 = 78
回主页
