三年级数学下册教案-3.2 列队表演(一) 北师大版
文档属性
| 名称 | 三年级数学下册教案-3.2 列队表演(一) 北师大版 | 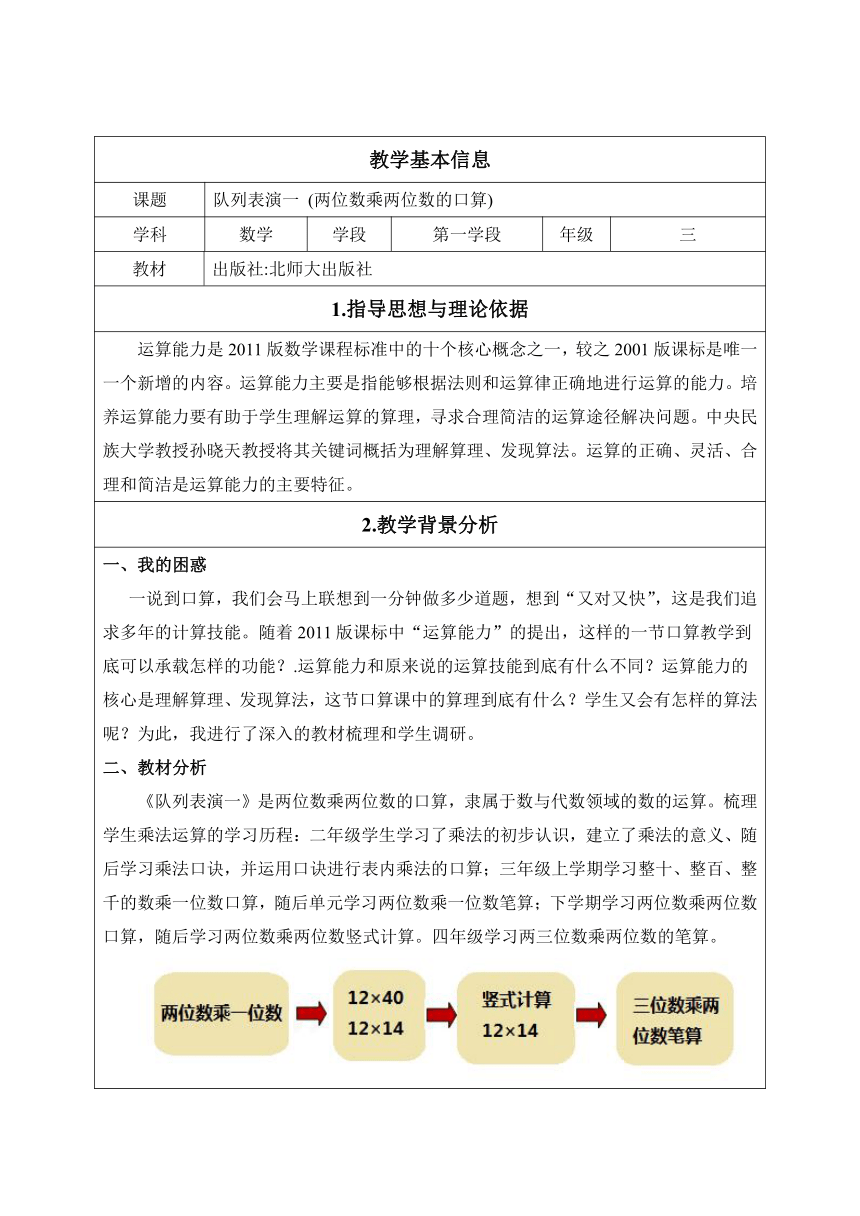 | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-26 19:59:10 | ||
图片预览


文档简介
教学基本信息
课题 队列表演一 (两位数乘两位数的口算)
学科 数学 学段 第一学段 年级 三
教材 出版社:北师大出版社
1.指导思想与理论依据
运算能力是2011版数学课程标准中的十个核心概念之一,较之2001版课标是唯一一个新增的内容。运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力要有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题。中央民族大学教授孙晓天教授将其关键词概括为理解算理、发现算法。运算的正确、灵活、合理和简洁是运算能力的主要特征。
2.教学背景分析
一、我的困惑 一说到口算,我们会马上联想到一分钟做多少道题,想到“又对又快”,这是我们追求多年的计算技能。随着2011版课标中“运算能力”的提出,这样的一节口算教学到底可以承载怎样的功能?.运算能力和原来说的运算技能到底有什么不同?运算能力的核心是理解算理、发现算法,这节口算课中的算理到底有什么?学生又会有怎样的算法呢?为此,我进行了深入的教材梳理和学生调研。
二、教材分析
《队列表演一》是两位数乘两位数的口算,隶属于数与代数领域的数的运算。梳理学生乘法运算的学习历程:二年级学生学习了乘法的初步认识,建立了乘法的意义、随后学习乘法口诀,并运用口诀进行表内乘法的口算;三年级上学期学习整十、整百、整千的数乘一位数口算,随后单元学习两位数乘一位数笔算;下学期学习两位数乘两位数口算,随后学习两位数乘两位数竖式计算。四年级学习两三位数乘两位数的笔算。
由上图可看出,“两位数乘两位数口算”放在“两位数乘两位数笔算”的前面。口算这节课若定位在算得又对又快的运算技能上,那么笔算那节课的意义又是什么?竖式笔算方便快捷,用竖式笔算一定会比口算的正确率要高?笔算前的这样一节口算到底有什么意义?
为此,我又认真分析了本课的教材:
虽然是口算,但是教材借助点子图模型来理解算理,并对应出现了乘法算式,沟通了模型和算法之间的联系。然后借助“表格”进一步理解算理。借助对点子图的操作,进行乘法的直观运算。从教材的意图来看,显然不是在关注计算技能,恰恰是关注通过直观的方式促进学生对算理的理解,在独立面对问题的过程中,让学生经历寻找算法的过程。
荷兰著名教育家弗兰登塔尔在(《作为教育任务的数学》中有这样的一段论述:……为了“快”的教学是一种类似于把学生训练成计算机的教育,即学生只能被动的执行程序,缺少自己发挥主动性和创造性的空间。其结果,不仅在计算方面人无法与计算机相比,反而极大的抑制了学生主动性和创造性的发展。
就这样的一节口算课,学生有没有主动需找算法的经验和知识呢?如果我们把课堂慢下来,努力给孩子们一些空间,他们会有怎样的创造呢?为此,我进行了学生调研:
三、学情分析
通过调研我们发现学生在面对新的问题时想法是非常丰富的,他们有面对新的运算问题,进行独立思考的能力,在学生探寻算法的过程中,我们真切的看到了孩子们丰富的创造性。我们只有尊重学生的想法才能调动他们学习的积极性,才是真正关注不同层次的学生。
四、我的思考
1. 给学生空间,为学生自主的需找算法提供机会。
2.借助直观,充分交流,为学生理解算法的合理性提供平台。
3.教学目标(含重难点)
教学目标: 1.结合情境经历寻找两位数乘两位数口算算法的思考的过程,借助直观理解算理。
2.了解点子图、表格是进行两位数乘两位数乘法的工具,在理解算理的基础上体验算法多样化,发展学生的运算能力。
3. 结合操作、理解算理的过程培养学生交流与表达能力及数学阅读和思考的能力。
教学重点:结合操作,理解两位数乘两位数乘法的算理。
教学难点:结合操作,理解算理,体验算法多样化。
4.教学过程与教学资源设计(可附教学流程图)
教学流程图:
教学过程:
一、创设情境 提出问题 尝试解决
(出示情境图)
问:学校组织队列表演,排成这样的队形,你观察到了什么数学信息?
问:想知道一共需要选拔多少名学生,你会列式吗?
预设:12×14
问:怎么得到12×14的结果?把你的想法写在纸上。(学生独立完成)
【设计意图:在真实的生活情境中,引导学生感受到现实生活动蕴含着大量的数学信息,生活中的一些问题,可以抽象成数学问题来解决】
二、借助直观 明确算理 体会算法多样化
1.展示学生的多种方法,要求学生认真看,思考:这些方法合理吗?
2.在小组内借助点子图把自己读懂的方法讲给同学听,并提出自己不懂的问题。
3.集体交流:
(1)请小组代表到台前讲自己读懂的一种方法(一人讲,一人同时在点子图上圈画)
学生活动:补充、质疑、评价。
(2)借助直观感悟方法之间的联系
问:看一看黑板上的方法,你有什么新发现?
【设计意图:交流分享是重要的学习活动,在分享的过程中,引导学生借助点子图的直观模型分一分,学生在表达中,体会直观对于理解思考过程的重要,也在实物与算法的勾连中理解算理。】
(3)小结:回忆解决12×4的过程,我们是怎么解决12×14的?
(预设两种方法:①利用乘法意义,把乘法转化为加法计算;②把其中一个两位数分成两部分,分别乘另一个两位数,再求和)。这些方法之间有什么联系?
【设计意图:学生的算法很多,但需要引导学生关注算法的合理性,这与培养学生运算能力的目标一致。在此环节中,通过结合实物的操作解释具体的计算过程,让学生感觉到无论是怎样算,怎样分,都是在计算14个12。利用乘法的意义支撑学生对合理性的判断。】
三、选择合适的方法计算18×14
1.选择你喜欢的方法独立解决“要排18排需要多少人?”
2.反馈学生做法。
统计每种方法有多少人,让学生说一说你为什么选择这种方法,体会不同方法的优势。
让做的又快又好的学生给大家介绍经验。(体会方法的简洁性)
【设计意图:算法的合理是运算能力的一个特征,但如何引导学生关注简洁呢?在此环节让学生自主选择运算方法,在交流分享中,让孩子表达他们心目中的简洁。】
四、回顾反思 总结提升
谈谈这节课的收获或感受。
对自己或他人的表现进行评价。
5.学习效果评价设计
30×15=450
4×15=60,
450+60=510
6.教学设计特色说明与教学反思
1.直观模型的介入,让抽象的算法变得合情合理
三年级学生处于形象思维向抽象思维转化的开始阶段,理解算理离不开操作和观察,为此,我们鼓励学生使用点子图理解算理,这样的有结构的学具,让道理被学生看得到、摸得着。
2.当我们慢了下来,看到了学生自主的探索和无限的创造
l 只要给学生留出较充分的探索空间,引导学生寻找,每个算法都可能被学生找到,都能成为发现和创造的富饶土壤。
课题 队列表演一 (两位数乘两位数的口算)
学科 数学 学段 第一学段 年级 三
教材 出版社:北师大出版社
1.指导思想与理论依据
运算能力是2011版数学课程标准中的十个核心概念之一,较之2001版课标是唯一一个新增的内容。运算能力主要是指能够根据法则和运算律正确地进行运算的能力。培养运算能力要有助于学生理解运算的算理,寻求合理简洁的运算途径解决问题。中央民族大学教授孙晓天教授将其关键词概括为理解算理、发现算法。运算的正确、灵活、合理和简洁是运算能力的主要特征。
2.教学背景分析
一、我的困惑 一说到口算,我们会马上联想到一分钟做多少道题,想到“又对又快”,这是我们追求多年的计算技能。随着2011版课标中“运算能力”的提出,这样的一节口算教学到底可以承载怎样的功能?.运算能力和原来说的运算技能到底有什么不同?运算能力的核心是理解算理、发现算法,这节口算课中的算理到底有什么?学生又会有怎样的算法呢?为此,我进行了深入的教材梳理和学生调研。
二、教材分析
《队列表演一》是两位数乘两位数的口算,隶属于数与代数领域的数的运算。梳理学生乘法运算的学习历程:二年级学生学习了乘法的初步认识,建立了乘法的意义、随后学习乘法口诀,并运用口诀进行表内乘法的口算;三年级上学期学习整十、整百、整千的数乘一位数口算,随后单元学习两位数乘一位数笔算;下学期学习两位数乘两位数口算,随后学习两位数乘两位数竖式计算。四年级学习两三位数乘两位数的笔算。
由上图可看出,“两位数乘两位数口算”放在“两位数乘两位数笔算”的前面。口算这节课若定位在算得又对又快的运算技能上,那么笔算那节课的意义又是什么?竖式笔算方便快捷,用竖式笔算一定会比口算的正确率要高?笔算前的这样一节口算到底有什么意义?
为此,我又认真分析了本课的教材:
虽然是口算,但是教材借助点子图模型来理解算理,并对应出现了乘法算式,沟通了模型和算法之间的联系。然后借助“表格”进一步理解算理。借助对点子图的操作,进行乘法的直观运算。从教材的意图来看,显然不是在关注计算技能,恰恰是关注通过直观的方式促进学生对算理的理解,在独立面对问题的过程中,让学生经历寻找算法的过程。
荷兰著名教育家弗兰登塔尔在(《作为教育任务的数学》中有这样的一段论述:……为了“快”的教学是一种类似于把学生训练成计算机的教育,即学生只能被动的执行程序,缺少自己发挥主动性和创造性的空间。其结果,不仅在计算方面人无法与计算机相比,反而极大的抑制了学生主动性和创造性的发展。
就这样的一节口算课,学生有没有主动需找算法的经验和知识呢?如果我们把课堂慢下来,努力给孩子们一些空间,他们会有怎样的创造呢?为此,我进行了学生调研:
三、学情分析
通过调研我们发现学生在面对新的问题时想法是非常丰富的,他们有面对新的运算问题,进行独立思考的能力,在学生探寻算法的过程中,我们真切的看到了孩子们丰富的创造性。我们只有尊重学生的想法才能调动他们学习的积极性,才是真正关注不同层次的学生。
四、我的思考
1. 给学生空间,为学生自主的需找算法提供机会。
2.借助直观,充分交流,为学生理解算法的合理性提供平台。
3.教学目标(含重难点)
教学目标: 1.结合情境经历寻找两位数乘两位数口算算法的思考的过程,借助直观理解算理。
2.了解点子图、表格是进行两位数乘两位数乘法的工具,在理解算理的基础上体验算法多样化,发展学生的运算能力。
3. 结合操作、理解算理的过程培养学生交流与表达能力及数学阅读和思考的能力。
教学重点:结合操作,理解两位数乘两位数乘法的算理。
教学难点:结合操作,理解算理,体验算法多样化。
4.教学过程与教学资源设计(可附教学流程图)
教学流程图:
教学过程:
一、创设情境 提出问题 尝试解决
(出示情境图)
问:学校组织队列表演,排成这样的队形,你观察到了什么数学信息?
问:想知道一共需要选拔多少名学生,你会列式吗?
预设:12×14
问:怎么得到12×14的结果?把你的想法写在纸上。(学生独立完成)
【设计意图:在真实的生活情境中,引导学生感受到现实生活动蕴含着大量的数学信息,生活中的一些问题,可以抽象成数学问题来解决】
二、借助直观 明确算理 体会算法多样化
1.展示学生的多种方法,要求学生认真看,思考:这些方法合理吗?
2.在小组内借助点子图把自己读懂的方法讲给同学听,并提出自己不懂的问题。
3.集体交流:
(1)请小组代表到台前讲自己读懂的一种方法(一人讲,一人同时在点子图上圈画)
学生活动:补充、质疑、评价。
(2)借助直观感悟方法之间的联系
问:看一看黑板上的方法,你有什么新发现?
【设计意图:交流分享是重要的学习活动,在分享的过程中,引导学生借助点子图的直观模型分一分,学生在表达中,体会直观对于理解思考过程的重要,也在实物与算法的勾连中理解算理。】
(3)小结:回忆解决12×4的过程,我们是怎么解决12×14的?
(预设两种方法:①利用乘法意义,把乘法转化为加法计算;②把其中一个两位数分成两部分,分别乘另一个两位数,再求和)。这些方法之间有什么联系?
【设计意图:学生的算法很多,但需要引导学生关注算法的合理性,这与培养学生运算能力的目标一致。在此环节中,通过结合实物的操作解释具体的计算过程,让学生感觉到无论是怎样算,怎样分,都是在计算14个12。利用乘法的意义支撑学生对合理性的判断。】
三、选择合适的方法计算18×14
1.选择你喜欢的方法独立解决“要排18排需要多少人?”
2.反馈学生做法。
统计每种方法有多少人,让学生说一说你为什么选择这种方法,体会不同方法的优势。
让做的又快又好的学生给大家介绍经验。(体会方法的简洁性)
【设计意图:算法的合理是运算能力的一个特征,但如何引导学生关注简洁呢?在此环节让学生自主选择运算方法,在交流分享中,让孩子表达他们心目中的简洁。】
四、回顾反思 总结提升
谈谈这节课的收获或感受。
对自己或他人的表现进行评价。
5.学习效果评价设计
30×15=450
4×15=60,
450+60=510
6.教学设计特色说明与教学反思
1.直观模型的介入,让抽象的算法变得合情合理
三年级学生处于形象思维向抽象思维转化的开始阶段,理解算理离不开操作和观察,为此,我们鼓励学生使用点子图理解算理,这样的有结构的学具,让道理被学生看得到、摸得着。
2.当我们慢了下来,看到了学生自主的探索和无限的创造
l 只要给学生留出较充分的探索空间,引导学生寻找,每个算法都可能被学生找到,都能成为发现和创造的富饶土壤。
