【八下优化训练】第十八章 平行四边形(含解析)
文档属性
| 名称 | 【八下优化训练】第十八章 平行四边形(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 07:17:38 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2020-2021学年度人教版八年级数学下册优化全方位训练
第十八章
平行四边形
题号
一
二
三
总分
得分
考试时间:100分钟
满分:100分
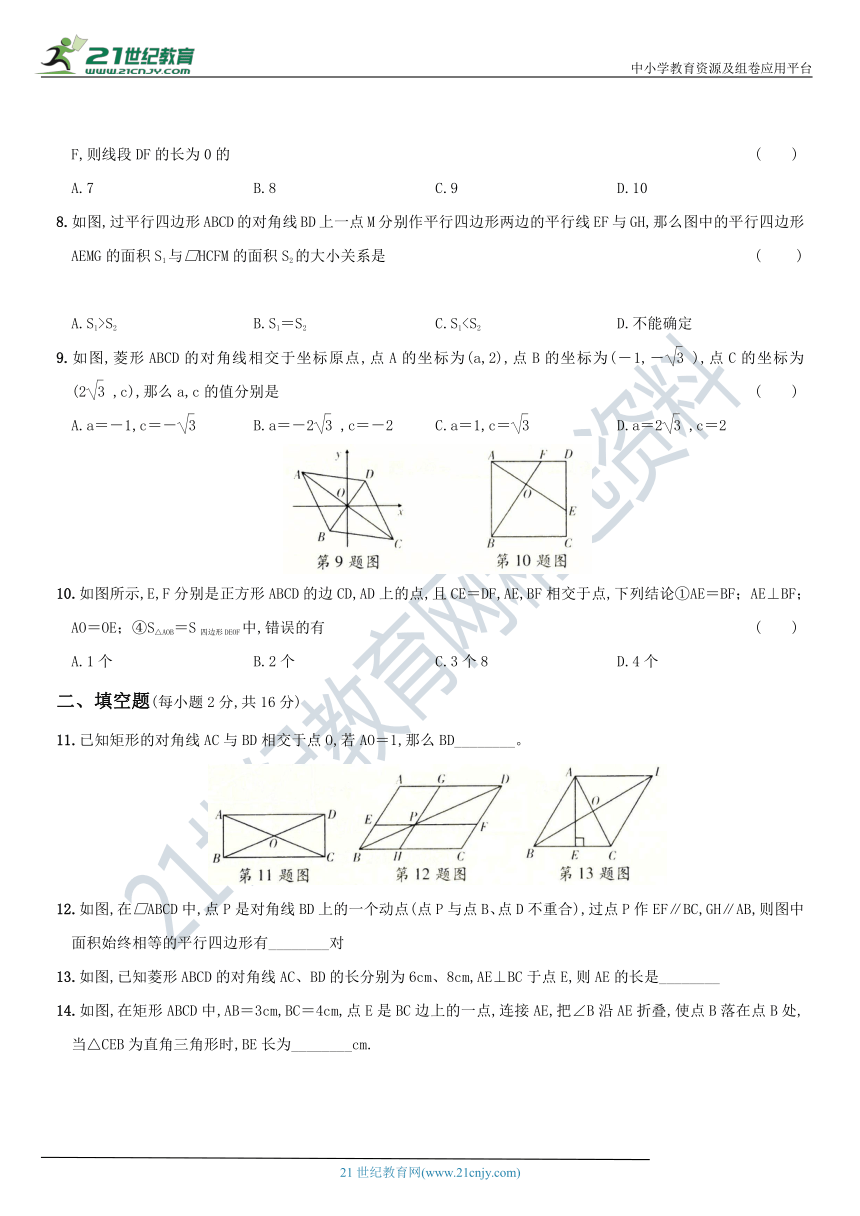
一、选择题(本大题共10小题,每小题3分,共30分.在每小题的4个选项中,只有一个选项是符合题目要求的)
1.下列语句正确的是
(
)
A.对角线互相垂直的四边形是菱形
B.有两边及一角对应相等的两个三角形全等
C.矩形的对角线相等
D.平行四边形是轴对称图形
2.在□ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则□ABCD的周长是
(
)
A.22
B.20
C.22或20
D.18
3.如图,在□ABCD中,AD=8,点E,F分别是BD,CD的中点,直则EF等于
(
)
A.
2
B.3
C.4
D.5
4.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为
(
)
A.13
B.14
C.15
D.16
5.如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标为
(
)
A.(-5,4)
B.(-5,5)
C.(-4,4)
D.(-4,3)
6.如图,在菱形ABCD中,BE⊥AD,BF⊥CD,E、F为垂足,AE=ED,则∠EBF等于
(
)
A.75°
B.60°
C.50°
D.45°
7.如图,在△ABC中,∠B=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为0的
(
)
A.7
B.8
C.9
D.10
8.如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与□HCFM的面积S2的大小关系是
(
)
A.S1>S2
B.S1=S2
C.S1D.不能确定
9.如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-),点C的坐标为(2,c),那么a,c的值分别是
(
)
A.a=-1,c=-
B.a=-2,c=-2
C.a=1,c=
D.a=2,c=2
10.如图所示,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点,下列结论①AE=BF;AE⊥BF;AO=OE;④S△AOB=S四边形DEOF中,错误的有
(
)
A.1个
B.2个
C.3个8
D.4个
二、填空题(每小题2分,共16分)
11.已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD________。
12.如图,在□ABCD中,点P是对角线BD上的一个动点(点P与点B、点D不重合),过点P作EF∥BC,GH∥AB,则图中面积始终相等的平行四边形有________对
13.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是________
14.如图,在矩形ABCD中,AB=3cm,BC=4cm,点E是BC边上的一点,连接AE,把∠B沿AE折叠,使点B落在点B处,当△CEB为直角三角形时,BE长为________cm.
15.如图,△ABC中,D是边AB上一点,O是边AC的中点,连接DO并延长到点E,使OE=DO,连接DC,CE,EA,则四边形ADCE的形状是________
16.如图,正方形ABCD的面积为5,正方形BEFG的面积为4,那么△GCE的面积是________
17.如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=60°,连接EF,则△AEF的面积最小值是________
18.如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________
三、解答题(本题共8小题,共54分)
19.(6分)如图,在□ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由
20.(6分)如图,□ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.求证:四边形EGFH是平行四边形
21.(6分)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将四△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形
22.(6分)如图,已知□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点E.
(1)试说明线段CD与FA相等的理由;
(2)若要使∠F=∠BCF,□ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线)
23.(6分)如图,点E、F为线段BD的两个三等分点,四边形AECF是菱形
(1)试判断四边形ABCD的形状,并加以证明;
(2)若菱形AECF的周长为20,BD为24,试求四边形ABCD的面积
24.(6分)将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下求折痕EF的长
25.(8分)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从点A向点D以1cm/s的速度运动,到点D即停止点Q从点C向点B以2cm/s的速度运动,到点B即停止直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
26.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE。
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由。
※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
《参考答案及解析》
第十八章
测评卷
1.C
【解析】对角线互相垂直且平分的四边形是菱形,故A错误;两边及其夹角对应相等的两个三角形全等,故B错误;矩形的对角线相等,故C正确;平行四边形是中心对称图形,故D错误
2.C
【解析】在□ABCD中,AD∥BC,则∠AEB=∠DAE.∵AE平分∠BAD∴∠Bae=∠dae=∠aeb,∴ab=BE.
①当BE=3时,周长=(BC+AB)×2=(3+4+3)×2=20
当BE=4时,周长=(BC+AB)×2=(4+3+4)×2=22.
3.C
【解析】∵点E,F分别是BD,CD的中点,
∴EF是△BCD的中位线,∴bc=2EF.
∵AD=8,四边形ABCD是平行四边形,
∴BC=AD=8,∴EF=4.
4.D
【解析】如图所示:
∵四边形ABCD是平行四边形,∴AD∥BC,∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,∴∠DAE=∠BAE,∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,∴AF=BE
∴四边形ABEF是平行四边形,∵AB=AF,∴四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF=BF=6,∴OA===8,
∴AE=20A=16
5.A
【解析】A(3,0),B(0,4),OA=3,OB=4,
∴AB==5,∵四边形ABCD是菱形,∴BC=AD=AB=5,∴点C的坐标为(-5,4)
6.B
【解析】连接BD
∵BE⊥AD,AE=ED,∴BD=AB=AD,∴△ABD是等边三角形,∴∠A=60°,
又∵BE⊥AD,BF⊥CD,∴∠BED+∠BFD=180°,∴∠ADC+∠EBF=180°,
又∵∠ADC+∠A=180°,∴∠EBF=∠A=60°
7.B
【解析】在Rt△ABC中,∠ABC=90°,AB=8,BC=6,∴AC===10,
∵DE是△ABC的中位线,∴DF∥BM,DE=BC=3,
∴∠EFC=∠FCM,∵∠FCE=∠FCM,∴∠EFC=∠ECF,∴EC=EF=AC=5,∴DF=DE+EF=3+5=8.
8.B
【解析】四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
∴△ABD≌△CDB(SSS),即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2
9.B
【解析】四边形ABCD为菱形,∴OA=OC,
又∵点O为坐标原点,∴点A和点C关于原点对称,
∵点A的坐标为(a,2),点C的坐标为(2,c),∴a=-2,c=-2
10.A
【解析】四边形ABCD是正方形,∴CD=AD.
∵CE=DF,∴DE=AF,又∵AD=AB,∠BAF=∠D=90°,
∴△ADE≌△BAF,∴AE=BF,S△ADE=S△BAF,
∠Dea=∠AFB,∠EAD=∠FBA,∴S△AOB=S四边形DEOF,故①、④正确
∵∠ABF+∠AFB=∠DAE+∠DEA=90°∴∠AFB+∠EAF=90°,
∴AE⊥BF,故②正确.错误的结论是:③AO=OE
11.2
【解析】在矩形ABCD中,∵对角线AC与BD相交于点
O,AO=1,∴AO=CO=BO=DO=1,∴BD=2.
12.3
【解析】∵四边形ABCD是平行四边形,∴S△ABD=S△CBD
∵BP是平行四边形BEPH的对角线,∴S△BEP=S△BHP,
∵pD是平行
GPFD四边形的对角线,
∴S△GPD=S△FPD
∴s△ABD-S△BEP-S△GPD=S△BCD-S△BHP-S△PFD,即S□AEPG
=S□HCFP,
∴
S□ABHG=S□BCFE,
同理
S□AEFD=S□GDCH
即
S□ABHC
=S□BCFE
,S□AGPE
=S□HCFP,
S□AEFD
=S□GDCH
13.cm
【解析】∵四边形ABCD是菱形,∴CO=AC=3cm,BO=BD=4cm,AO⊥BO,
∴BC==5cm,
∵S菱形ABCD==×6×8=24cm2,S菱形ABCD=BC×AE,
∴BC×AE=24,∴AE==cm.
14.或3
【解析】如图1中,当A,B′,C共线时,∠EB′C=90°
∵四边形ABCD是矩形,∴∠B=90°,
∴AC===5,
∵AB=AB′=3,
∴CB′=5-3=2,设BE=EB′
=x,则EC=4-x,
在Rt△CEB′中,CE2=B′E2+B′C2,
∴(4-x)2=22+x2,
∴x=,
如图2中,当点B′落在AD上时,
∠CE′B=90°,
此时四边形ABEB′是正方形,
∴BE=AB=3,
综上所述,满足条件的BE的值为或3.
15.平行四边形
【解析】∵0是AC的中点,∴OA=OC.∵OE=DO,∴四边形ADCE是平行四边形
16.-2【解析】∵正方形ABCD的面积为5,正方形BEFG的面积为4,
∴正方形ABCD的边长为,正方形BEFG的边长为2,∴CE=-2,△GCE的面积
CE·BG=×(-2)×2=-2
17.3【解析】连接AC.
则△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
∴∠B=∠ACF=60°,
∵AD∥BC,∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,
∠AFC=∠D+∠FAD=60°+∠FAD,
∴∠AEB=∠AFC,
在△ABE和△ACF中,
.
∴△ABE≌△ACF(AAS),∴AE=AF,
∵∠EAF=60°,∴△AEF是等边三角形,
∴AE=2,
∴△AEF任意一边上的高=
eq
\r((2)2-()2)
=3.
∴△AEF的面积最小值=×3×2=3
18.6【解析】设BE与AC交于点P,连接BD,
∵点B与D关于AC对称,∴PD=PB
∴pd+pe=pB+pE=BE最小
即P在AC与BE的交点上时,PD+PE最小,为BE的长度;
∵正方形ABCD的边长为6,∴AB=6
又∵△ABE是等边三角形,∴BE=AB=6
故所求最小值为6.
19.解:∠AFC=∠AEC,理由如下:平行四边形ABCD中,BC∥AD,又AE∥CF,∴四边形AECF为平行四边形,
∴∠AEC=∠AFC
20.证明:四边形ABCD为平行四边形,∴AD∥BC∴∠EAO=∠FCO
∵O为AC的中点,∴OA=OC
在△OAE和△OCF中,
∴△OAE≌△OCF(ASA)∴
OE=OF.
同理可证得OG=OH
∴四边形EGFH是平行四边形
21.证明:由平移变换的性质得:CF=AD=10cm,DF=AC,
∵∠B=90°,AB=6,BC=8,
∴AC===10,
∴AC=DF=AD=CF=10,
∴四边形ACFD是菱形。
22.(1)∵证明四边形ABCD是平行四边形,∴CD∥AB
又∵CE的延长线交BA的延长线于点F,∴∠CDA=∠DAF;
∵E是AD中点,∴DE=AE.
∵∠CED=∠AEF
∴△CDE≌△FAE
∴CD=AF.
(2)解:要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB
证明:∵由(1)知,△CDE≌△FAE,∴CD=AF
又∵四边形ABCD是平行四边形,∴CD=AB
∴AB=AF,即BF=2AB
∵BC=2AB
∴BF=BC,
∴∠F=∠BCF
23.解:(1)四边形ABCD为菱形理由如下:如图,连接AC交BD于点O,
∵四边形AECF是菱形,∴AC⊥BD,AO=OC,EO=OF,
又∵点E、F为线段BD的两个三等分点,∴BE=FD,BO=OD,
∵AO=OC,∴四边形ABCD为平行四边形,∵AC⊥BD,∴四边形ABCD为菱形;
(2)∵四边形AECF为菱形,且周长为20,AE=5,BD=24,∴EF=8,OE=EF=×8=4,
由勾股定理得,AO===3,∴AC=2AO=2×3=6,
s四边形ABCD=bd·ac=×24×6=72.
24.(1)证明∵矩形ABCD折叠使A,C重合,折痕为EF,∴OA=OC,EF⊥AC,EA=EC,∵AD∥BC,∴∠FAC=∠ECA,在
△AOF和△COE中,,∴△AOF≌△COE
∴OF=OE,∵OA=OC,AC⊥EF,∴四边形AECF为菱形;
(2)解:设菱形的边长为x,则BE=BC-CE=8-x,AE=x
在Rt△ABE中,
,∴(8-x)2+42=x2,解得x=5,即菱形的边长为5;
(3)解:在Rt△ABC中,AC===4,∴OA=AC=2,在Rt△AOE中,
OE==
eq
\r(52-(2)2)
=,∴EF=2OE=2
25.解:设当P,Q两点同时出发ts后,四边形ABQP或四边形PQCD是平行四边形
根据题意,得AP=tcm,PD=(24-t)cm,CQ=2tcm,BQ=(30-2t)cm(0≤t≤15).
①若四边形ABQP是平行四边形,∵AD∥BC,∴还需满足AP=BQ
∴t=30-2t.解得t=10.
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,∵AD∥BC,∴还需满足PD=CQ
∴24-t=2t.解得t=8.
∴8s后四边形PQCD是平行四边形
综上所述:当P,Q两点同时出发8秒或10秒后,所截得两个四边形中其中一个四边形为平行四边形
26.(1)证明:∵DE⊥BC,∴∠DFB=90°
又∵∠ACB=90°,∴∠ACB=∠DFB
∴AC∥DE
又MN∥AB,即CE∥AD
D.,
∴四边形ADEC是平行四边形
∴CE=AD.
(2)解:四边形BECD是菱形。
理由:∵D为AB中点,∴AD=BD
又由(1)得CE=AD,∴BD=CE
又∵BD∥CE,∴四边形BECD是平行四边形
又∵DE⊥BC,∴四边形BECD是菱形
(3)解:当∠A=45°时,四边形BECD是正方形。理由:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°∴AC=BC
又∵D为AB中点,CD⊥AB,即∠CDB=90°
又∵四边形BECD是菱形,∴四边形BECD是正方形
∴当∠A=45°时,四边形BECD是正方形
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
2020-2021学年度人教版八年级数学下册优化全方位训练
第十八章
平行四边形
题号
一
二
三
总分
得分
考试时间:100分钟
满分:100分
一、选择题(本大题共10小题,每小题3分,共30分.在每小题的4个选项中,只有一个选项是符合题目要求的)
1.下列语句正确的是
(
)
A.对角线互相垂直的四边形是菱形
B.有两边及一角对应相等的两个三角形全等
C.矩形的对角线相等
D.平行四边形是轴对称图形
2.在□ABCD中,∠A的平分线把BC边分成长度是3和4的两部分,则□ABCD的周长是
(
)
A.22
B.20
C.22或20
D.18
3.如图,在□ABCD中,AD=8,点E,F分别是BD,CD的中点,直则EF等于
(
)
A.
2
B.3
C.4
D.5
4.如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为
(
)
A.13
B.14
C.15
D.16
5.如图,四边形ABCD是菱形,A(3,0),B(0,4),则点C的坐标为
(
)
A.(-5,4)
B.(-5,5)
C.(-4,4)
D.(-4,3)
6.如图,在菱形ABCD中,BE⊥AD,BF⊥CD,E、F为垂足,AE=ED,则∠EBF等于
(
)
A.75°
B.60°
C.50°
D.45°
7.如图,在△ABC中,∠B=90°,AB=8,BC=6.若DE是△ABC的中位线,延长DE交△ABC的外角∠ACM的平分线于点F,则线段DF的长为0的
(
)
A.7
B.8
C.9
D.10
8.如图,过平行四边形ABCD的对角线BD上一点M分别作平行四边形两边的平行线EF与GH,那么图中的平行四边形AEMG的面积S1与□HCFM的面积S2的大小关系是
(
)
A.S1>S2
B.S1=S2
C.S1
9.如图,菱形ABCD的对角线相交于坐标原点,点A的坐标为(a,2),点B的坐标为(-1,-),点C的坐标为(2,c),那么a,c的值分别是
(
)
A.a=-1,c=-
B.a=-2,c=-2
C.a=1,c=
D.a=2,c=2
10.如图所示,E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点,下列结论①AE=BF;AE⊥BF;AO=OE;④S△AOB=S四边形DEOF中,错误的有
(
)
A.1个
B.2个
C.3个8
D.4个
二、填空题(每小题2分,共16分)
11.已知矩形的对角线AC与BD相交于点O,若AO=1,那么BD________。
12.如图,在□ABCD中,点P是对角线BD上的一个动点(点P与点B、点D不重合),过点P作EF∥BC,GH∥AB,则图中面积始终相等的平行四边形有________对
13.如图,已知菱形ABCD的对角线AC、BD的长分别为6cm、8cm,AE⊥BC于点E,则AE的长是________
14.如图,在矩形ABCD中,AB=3cm,BC=4cm,点E是BC边上的一点,连接AE,把∠B沿AE折叠,使点B落在点B处,当△CEB为直角三角形时,BE长为________cm.
15.如图,△ABC中,D是边AB上一点,O是边AC的中点,连接DO并延长到点E,使OE=DO,连接DC,CE,EA,则四边形ADCE的形状是________
16.如图,正方形ABCD的面积为5,正方形BEFG的面积为4,那么△GCE的面积是________
17.如图,菱形ABCD中,AB=4,∠B=60°,E,F分别是BC,DC上的点,∠EAF=60°,连接EF,则△AEF的面积最小值是________
18.如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为________
三、解答题(本题共8小题,共54分)
19.(6分)如图,在□ABCD中,点E,F分别在BC,AD上,AE∥CF,请说明∠AFC与∠AEC的大小关系,并说明理由
20.(6分)如图,□ABCD中,点O是对角线AC的中点,EF过点O,与AD,BC分别相交于点E,F,GH过点O,与AB,CD分别相交于点G,H,连接EG,FG,FH,EH.求证:四边形EGFH是平行四边形
21.(6分)如图,△ABC中,∠B=90°,AB=6cm,BC=8cm.将四△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形
22.(6分)如图,已知□ABCD中,E为AD的中点,CE的延长线交BA的延长线于点E.
(1)试说明线段CD与FA相等的理由;
(2)若要使∠F=∠BCF,□ABCD的边长之间还需再添加一个什么条件?请你补上这个条件,并说明你的理由(不要再增添辅助线)
23.(6分)如图,点E、F为线段BD的两个三等分点,四边形AECF是菱形
(1)试判断四边形ABCD的形状,并加以证明;
(2)若菱形AECF的周长为20,BD为24,试求四边形ABCD的面积
24.(6分)将矩形ABCD折叠使A,C重合,折痕交BC于E,交AD于F,
(1)求证:四边形AECF为菱形;
(2)若AB=4,BC=8,求菱形的边长;
(3)在(2)的条件下求折痕EF的长
25.(8分)如图所示,在四边形ABCD中,AD∥BC,AD=24cm,BC=30cm,点P从点A向点D以1cm/s的速度运动,到点D即停止点Q从点C向点B以2cm/s的速度运动,到点B即停止直线PQ将四边形ABCD截成两个四边形,分别为四边形ABQP和四边形PQCD,则当P,Q两点同时出发,几秒后所截得两个四边形中,其中一个四边形为平行四边形?
26.(10分)如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE。
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由。
※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※
《参考答案及解析》
第十八章
测评卷
1.C
【解析】对角线互相垂直且平分的四边形是菱形,故A错误;两边及其夹角对应相等的两个三角形全等,故B错误;矩形的对角线相等,故C正确;平行四边形是中心对称图形,故D错误
2.C
【解析】在□ABCD中,AD∥BC,则∠AEB=∠DAE.∵AE平分∠BAD∴∠Bae=∠dae=∠aeb,∴ab=BE.
①当BE=3时,周长=(BC+AB)×2=(3+4+3)×2=20
当BE=4时,周长=(BC+AB)×2=(4+3+4)×2=22.
3.C
【解析】∵点E,F分别是BD,CD的中点,
∴EF是△BCD的中位线,∴bc=2EF.
∵AD=8,四边形ABCD是平行四边形,
∴BC=AD=8,∴EF=4.
4.D
【解析】如图所示:
∵四边形ABCD是平行四边形,∴AD∥BC,∠DAE=∠AEB,
∵∠BAD的平分线交BC于点E,∴∠DAE=∠BAE,∴∠BAE=∠BEA,
∴AB=BE,同理可得AB=AF,∴AF=BE
∴四边形ABEF是平行四边形,∵AB=AF,∴四边形ABEF是菱形,
∴AE⊥BF,OA=OE,OB=OF=BF=6,∴OA===8,
∴AE=20A=16
5.A
【解析】A(3,0),B(0,4),OA=3,OB=4,
∴AB==5,∵四边形ABCD是菱形,∴BC=AD=AB=5,∴点C的坐标为(-5,4)
6.B
【解析】连接BD
∵BE⊥AD,AE=ED,∴BD=AB=AD,∴△ABD是等边三角形,∴∠A=60°,
又∵BE⊥AD,BF⊥CD,∴∠BED+∠BFD=180°,∴∠ADC+∠EBF=180°,
又∵∠ADC+∠A=180°,∴∠EBF=∠A=60°
7.B
【解析】在Rt△ABC中,∠ABC=90°,AB=8,BC=6,∴AC===10,
∵DE是△ABC的中位线,∴DF∥BM,DE=BC=3,
∴∠EFC=∠FCM,∵∠FCE=∠FCM,∴∠EFC=∠ECF,∴EC=EF=AC=5,∴DF=DE+EF=3+5=8.
8.B
【解析】四边形ABCD是平行四边形,EF∥BC,HG∥AB,
∴AD=BC,AB=CD,AB∥GH∥CD,AD∥EF∥BC,
∴四边形HBEM、GMFD是平行四边形,
在△ABD和△CDB中,
∴△ABD≌△CDB(SSS),即△ABD和△CDB的面积相等;
同理△BEM和△MHB的面积相等,△GMD和△FDM的面积相等,
故四边形AEMG和四边形HCFM的面积相等,即S1=S2
9.B
【解析】四边形ABCD为菱形,∴OA=OC,
又∵点O为坐标原点,∴点A和点C关于原点对称,
∵点A的坐标为(a,2),点C的坐标为(2,c),∴a=-2,c=-2
10.A
【解析】四边形ABCD是正方形,∴CD=AD.
∵CE=DF,∴DE=AF,又∵AD=AB,∠BAF=∠D=90°,
∴△ADE≌△BAF,∴AE=BF,S△ADE=S△BAF,
∠Dea=∠AFB,∠EAD=∠FBA,∴S△AOB=S四边形DEOF,故①、④正确
∵∠ABF+∠AFB=∠DAE+∠DEA=90°∴∠AFB+∠EAF=90°,
∴AE⊥BF,故②正确.错误的结论是:③AO=OE
11.2
【解析】在矩形ABCD中,∵对角线AC与BD相交于点
O,AO=1,∴AO=CO=BO=DO=1,∴BD=2.
12.3
【解析】∵四边形ABCD是平行四边形,∴S△ABD=S△CBD
∵BP是平行四边形BEPH的对角线,∴S△BEP=S△BHP,
∵pD是平行
GPFD四边形的对角线,
∴S△GPD=S△FPD
∴s△ABD-S△BEP-S△GPD=S△BCD-S△BHP-S△PFD,即S□AEPG
=S□HCFP,
∴
S□ABHG=S□BCFE,
同理
S□AEFD=S□GDCH
即
S□ABHC
=S□BCFE
,S□AGPE
=S□HCFP,
S□AEFD
=S□GDCH
13.cm
【解析】∵四边形ABCD是菱形,∴CO=AC=3cm,BO=BD=4cm,AO⊥BO,
∴BC==5cm,
∵S菱形ABCD==×6×8=24cm2,S菱形ABCD=BC×AE,
∴BC×AE=24,∴AE==cm.
14.或3
【解析】如图1中,当A,B′,C共线时,∠EB′C=90°
∵四边形ABCD是矩形,∴∠B=90°,
∴AC===5,
∵AB=AB′=3,
∴CB′=5-3=2,设BE=EB′
=x,则EC=4-x,
在Rt△CEB′中,CE2=B′E2+B′C2,
∴(4-x)2=22+x2,
∴x=,
如图2中,当点B′落在AD上时,
∠CE′B=90°,
此时四边形ABEB′是正方形,
∴BE=AB=3,
综上所述,满足条件的BE的值为或3.
15.平行四边形
【解析】∵0是AC的中点,∴OA=OC.∵OE=DO,∴四边形ADCE是平行四边形
16.-2【解析】∵正方形ABCD的面积为5,正方形BEFG的面积为4,
∴正方形ABCD的边长为,正方形BEFG的边长为2,∴CE=-2,△GCE的面积
CE·BG=×(-2)×2=-2
17.3【解析】连接AC.
则△ABC是等边三角形,
∴AB=AC,∠ACB=60°,
∴∠B=∠ACF=60°,
∵AD∥BC,∴∠AEB=∠EAD=∠EAF+∠FAD=60°+∠FAD,
∠AFC=∠D+∠FAD=60°+∠FAD,
∴∠AEB=∠AFC,
在△ABE和△ACF中,
.
∴△ABE≌△ACF(AAS),∴AE=AF,
∵∠EAF=60°,∴△AEF是等边三角形,
∴AE=2,
∴△AEF任意一边上的高=
eq
\r((2)2-()2)
=3.
∴△AEF的面积最小值=×3×2=3
18.6【解析】设BE与AC交于点P,连接BD,
∵点B与D关于AC对称,∴PD=PB
∴pd+pe=pB+pE=BE最小
即P在AC与BE的交点上时,PD+PE最小,为BE的长度;
∵正方形ABCD的边长为6,∴AB=6
又∵△ABE是等边三角形,∴BE=AB=6
故所求最小值为6.
19.解:∠AFC=∠AEC,理由如下:平行四边形ABCD中,BC∥AD,又AE∥CF,∴四边形AECF为平行四边形,
∴∠AEC=∠AFC
20.证明:四边形ABCD为平行四边形,∴AD∥BC∴∠EAO=∠FCO
∵O为AC的中点,∴OA=OC
在△OAE和△OCF中,
∴△OAE≌△OCF(ASA)∴
OE=OF.
同理可证得OG=OH
∴四边形EGFH是平行四边形
21.证明:由平移变换的性质得:CF=AD=10cm,DF=AC,
∵∠B=90°,AB=6,BC=8,
∴AC===10,
∴AC=DF=AD=CF=10,
∴四边形ACFD是菱形。
22.(1)∵证明四边形ABCD是平行四边形,∴CD∥AB
又∵CE的延长线交BA的延长线于点F,∴∠CDA=∠DAF;
∵E是AD中点,∴DE=AE.
∵∠CED=∠AEF
∴△CDE≌△FAE
∴CD=AF.
(2)解:要使∠F=∠BCF,需平行四边形ABCD的边长之间是2倍的关系,即BC=2AB
证明:∵由(1)知,△CDE≌△FAE,∴CD=AF
又∵四边形ABCD是平行四边形,∴CD=AB
∴AB=AF,即BF=2AB
∵BC=2AB
∴BF=BC,
∴∠F=∠BCF
23.解:(1)四边形ABCD为菱形理由如下:如图,连接AC交BD于点O,
∵四边形AECF是菱形,∴AC⊥BD,AO=OC,EO=OF,
又∵点E、F为线段BD的两个三等分点,∴BE=FD,BO=OD,
∵AO=OC,∴四边形ABCD为平行四边形,∵AC⊥BD,∴四边形ABCD为菱形;
(2)∵四边形AECF为菱形,且周长为20,AE=5,BD=24,∴EF=8,OE=EF=×8=4,
由勾股定理得,AO===3,∴AC=2AO=2×3=6,
s四边形ABCD=bd·ac=×24×6=72.
24.(1)证明∵矩形ABCD折叠使A,C重合,折痕为EF,∴OA=OC,EF⊥AC,EA=EC,∵AD∥BC,∴∠FAC=∠ECA,在
△AOF和△COE中,,∴△AOF≌△COE
∴OF=OE,∵OA=OC,AC⊥EF,∴四边形AECF为菱形;
(2)解:设菱形的边长为x,则BE=BC-CE=8-x,AE=x
在Rt△ABE中,
,∴(8-x)2+42=x2,解得x=5,即菱形的边长为5;
(3)解:在Rt△ABC中,AC===4,∴OA=AC=2,在Rt△AOE中,
OE==
eq
\r(52-(2)2)
=,∴EF=2OE=2
25.解:设当P,Q两点同时出发ts后,四边形ABQP或四边形PQCD是平行四边形
根据题意,得AP=tcm,PD=(24-t)cm,CQ=2tcm,BQ=(30-2t)cm(0≤t≤15).
①若四边形ABQP是平行四边形,∵AD∥BC,∴还需满足AP=BQ
∴t=30-2t.解得t=10.
∴10s后四边形ABQP是平行四边形;
②若四边形PQCD是平行四边形,∵AD∥BC,∴还需满足PD=CQ
∴24-t=2t.解得t=8.
∴8s后四边形PQCD是平行四边形
综上所述:当P,Q两点同时出发8秒或10秒后,所截得两个四边形中其中一个四边形为平行四边形
26.(1)证明:∵DE⊥BC,∴∠DFB=90°
又∵∠ACB=90°,∴∠ACB=∠DFB
∴AC∥DE
又MN∥AB,即CE∥AD
D.,
∴四边形ADEC是平行四边形
∴CE=AD.
(2)解:四边形BECD是菱形。
理由:∵D为AB中点,∴AD=BD
又由(1)得CE=AD,∴BD=CE
又∵BD∥CE,∴四边形BECD是平行四边形
又∵DE⊥BC,∴四边形BECD是菱形
(3)解:当∠A=45°时,四边形BECD是正方形。理由:
∵∠ACB=90°,∠A=45°,
∴∠ABC=∠A=45°∴AC=BC
又∵D为AB中点,CD⊥AB,即∠CDB=90°
又∵四边形BECD是菱形,∴四边形BECD是正方形
∴当∠A=45°时,四边形BECD是正方形
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
