2020-2021学年鲁教五四新版六年级下册数学期末练习试题(Word版有答案)
文档属性
| 名称 | 2020-2021学年鲁教五四新版六年级下册数学期末练习试题(Word版有答案) |  | |
| 格式 | zip | ||
| 文件大小 | 184.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 08:05:48 | ||
图片预览


文档简介
2020-2021学年鲁教五四新版六年级下册数学期末练习试题
一.选择题(共10小题,满分30分,每小题3分)
1.下列调查方式合适的是( )
A.为了了解市民对70周年国庆大阅兵的感受,小华在某校随机采访了8名初一学生
B.为了了解全校学生用于做数学作业的时间,小民同学在网上向6位好友做了调查
C.为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式
D.为了了解“北斗导航”卫星零部件的状况,检测人员采用了普查的方式
2.下列计算正确的有( )
①3﹣1=﹣3;
②(x2)3=x5;
③x3+x3=2x3;
④(π﹣3.14)0=1.
A.1个
B.2个
C.3个
D.4个
3.从五边形的一个顶点出发可以连接的对角线条数为( )
A.1
B.2
C.3
D.4
4.石墨烯是目前世界上最薄却又最坚硬同时还是导电性能最好的纳米材料,其理论厚度大约仅0.00000034毫米.将0.00000034用科学记数法表示为( )
A.3.4×10﹣7
B.3.4×10﹣8
C.34×10﹣8
D.0.34×10﹣6
5.小亮在计算(6x3y﹣3x2y2)÷3xy时,错把括号内的减号写成了加号,那么正确结果与错误结果的乘积是( )
A.2x2﹣xy
B.2x2+xy
C.4x4﹣x2y2
D.无法计算
6.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )
A.75°
B.90°
C.105°
D.115°
7.若单项式﹣8xay和x2yb的积为﹣2x5y6,则ab的值为( )
A.2
B.30
C.﹣15
D.15
8.下列各式中,正确的有( )
A.a3+a2=a5
B.x(x
m
)3=x3m
C.a8÷a2=a4
D.(﹣2a3)2=4a6
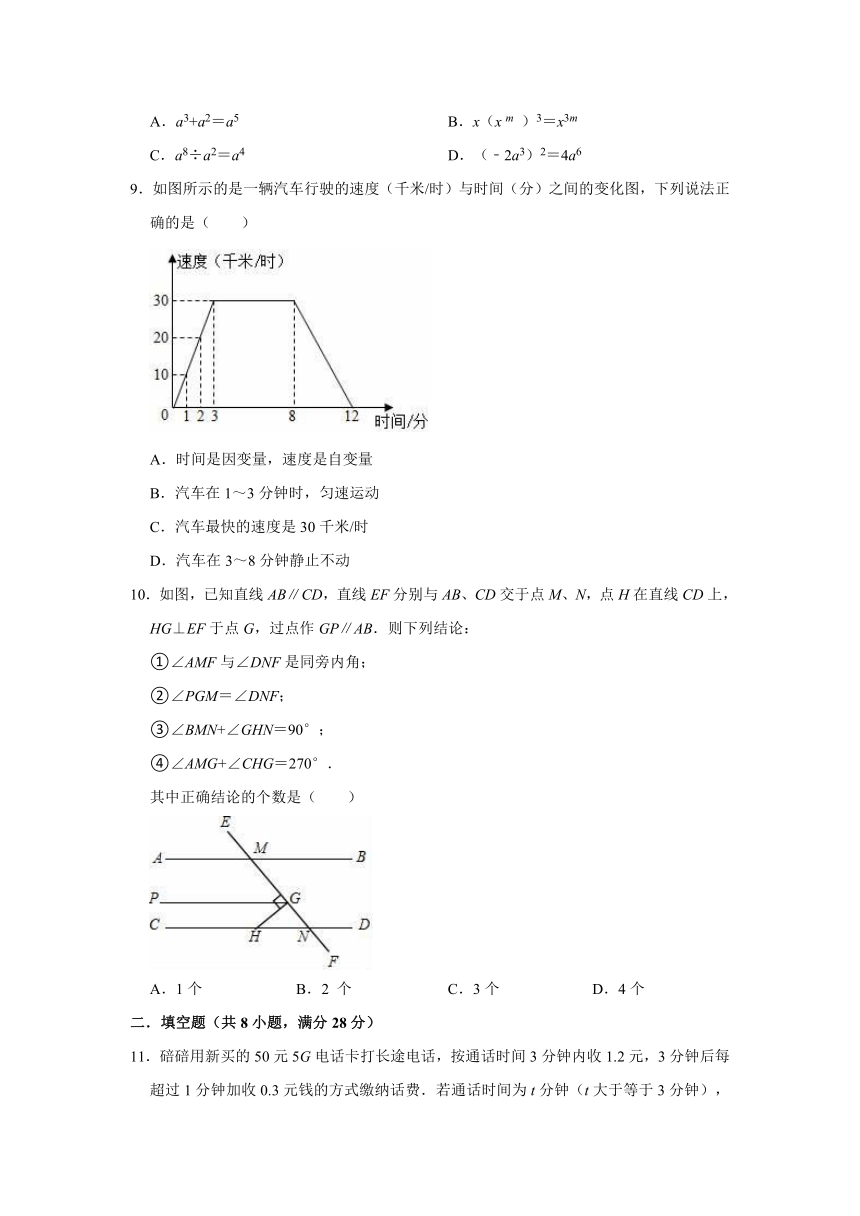
9.如图所示的是一辆汽车行驶的速度(千米/时)与时间(分)之间的变化图,下列说法正确的是( )
A.时间是因变量,速度是自变量
B.汽车在1~3分钟时,匀速运动
C.汽车最快的速度是30千米/时
D.汽车在3~8分钟静止不动
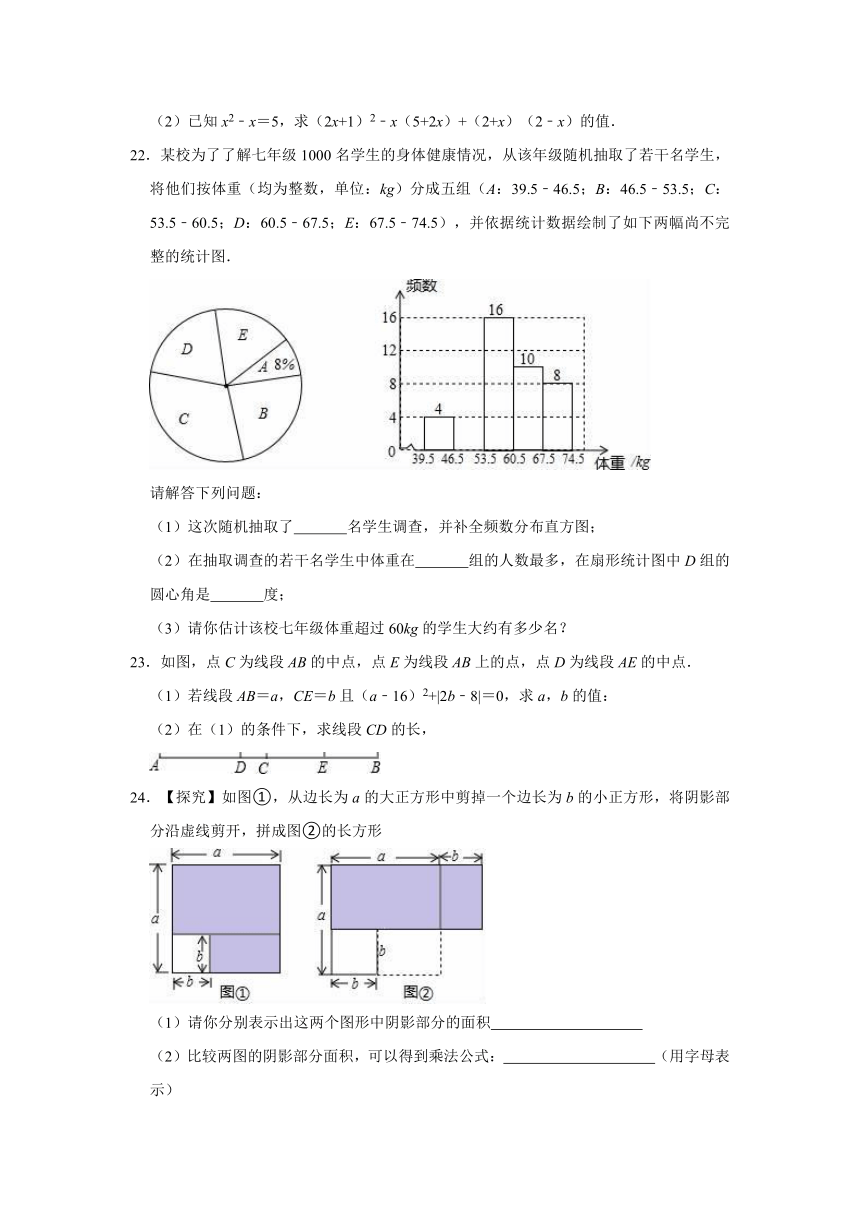
10.如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点作GP∥AB.则下列结论:
①∠AMF与∠DNF是同旁内角;
②∠PGM=∠DNF;
③∠BMN+∠GHN=90°;
④∠AMG+∠CHG=270°.
其中正确结论的个数是( )
A.1个
B.2
个
C.3个
D.4个
二.填空题(共8小题,满分28分)
11.碚碚用新买的50元5G电话卡打长途电话,按通话时间3分钟内收1.2元,3分钟后每超过1分钟加收0.3元钱的方式缴纳话费.若通话时间为t分钟(t大于等于3分钟),那么电话费用w(元)与时间t(分钟)的关系式可以表示为
.
12.如图,点C、D在线段AB上,点C为AB中点,若AC=5cm,BD=2cm,则CD=
cm.
13.若am?a2=a7,则m的值为
.
14.如图,AB∥CD,∠A=25°,∠C=70°,则∠E=
.
15.已知a2+b2=18,ab=﹣1,则a+b=
.
16.如图,射线OA的方向是北偏东20度,射线OB的方向是北偏西40度,OD是OB的反向延长线.若OC是∠AOD的平分线,则射线OC的方向是北偏东
度.
17.已知x+y=2,且(x﹣2)(y﹣2)=﹣3,则xy的值是
.
18.若a+b=2,a2﹣b2=6,则a﹣b=
.
三.解答题(共7小题,满分62分)
19.计算:[(2x﹣y)2+(x﹣y)(x+y)﹣2x(x﹣2y)]÷3x.
20.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的5倍.
求:(1)∠AOD、∠BOD的度数;
(2)∠BOE的度数.
21.(1)已知,y=3,求多项式[(2x﹣y)(2x+y)﹣y(6x﹣y)]÷2x的值;
(2)已知x2﹣x=5,求(2x+1)2﹣x(5+2x)+(2+x)(2﹣x)的值.
22.某校为了了解七年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5﹣46.5;B:46.5﹣53.5;C:53.5﹣60.5;D:60.5﹣67.5;E:67.5﹣74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
请解答下列问题:
(1)这次随机抽取了
名学生调查,并补全频数分布直方图;
(2)在抽取调查的若干名学生中体重在
组的人数最多,在扇形统计图中D组的圆心角是
度;
(3)请你估计该校七年级体重超过60kg的学生大约有多少名?
23.如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b且(a﹣16)2+|2b﹣8|=0,求a,b的值:
(2)在(1)的条件下,求线段CD的长,
24.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式:
(用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
25.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、为了了解市民对70周年国庆大阅兵的感受,小华在某校随机采访了8名初一学生,8名初一学生不具有代表性,调查方式不合适;
B、为了了解全校学生用于做数学作业的时间,小民同学在网上向6位好友做了调查,小民的6位好友不具有代表性,调查方式不合适;
C、为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式,普查的意义或价值不大,应选择抽样调查,调查方式不合适;
D、为了了解“北斗导航”卫星零部件的状况,检测人员采用了普查的方式,调查方式合适;
故选:D.
2.解:①;
②(x2)3=x6;
③x3+x3=2x3;
④(π﹣3.14)0=1.
∴正确的有③④共2个.
故选:B.
3.解:∵n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线,
∴从五边形的一个顶点出发可以画出5﹣3=2(条)对角线.
故选:B.
4.解:0.00000034=3.4×10﹣7.
故选:A.
5.解:正确结果为:
原式=6x3y÷3xy﹣3x2y2÷3xy
=2x2﹣xy,
错误结果为:
原式=6x3y÷3xy+3x2y2÷3xy
=2x2+xy,
∴(2x2﹣xy)(2x2+xy)=4x4﹣x2y2,
故选:C.
6.解:∵AB∥EF,
∴∠BDE=∠E=45°,
又∵∠A=30°,
∴∠B=60°,
∴∠1=∠BDE+∠B=45°+60°=105°,
故选:C.
7.解:﹣8xay×x2yb=﹣2xa+2yb+1=﹣2x5y6,
∴a+2=5,b+1=6,
解得a=3,b=5,
∴ab=3×5=15,
故选:D.
8.解:A、a3+a2,无法合并,故此选项错误;
B、x(x
m
)3=x3m+1,故此选项错误;
C、a8÷a2=a6,故此选项错误;
D、(﹣2a3)2=4a6,正确.
故选:D.
9.解:速度是因变量,时间是自变量,故选项A不合题意;
汽车在1~3分钟时,速度在增加,故选项B不合题意;
汽车最快速度是30千米/时,故选项C符合题意;
汽车在3~8分钟,匀速运动,故选项D不合题意;
故选:C.
10.解:∵∠AMF与∠DNF不是同旁内角,
∴①错误;
∵AB∥CD,GP∥AB,
∴AB∥CD∥GP,
∴∠PGM=∠CNM=∠DNF,∠BMN=∠HNG,∠AMN+∠HNG=180°,故②正确;
∵HG⊥MN,
∴∠HNG+∠GHN=90°,
∴∠BMN+∠GHN=90°,故③正确;
∵∠CHG=∠MNH+∠HGN,
∴∠MNH=∠CHG﹣90°,
∴∠AMN+∠HNG=∠AMN+∠CHG﹣90°=180°,
∴∠AMG+∠CHG=270°,故④正确,
故选:C.
二.填空题(共8小题,满分28分)
11.解:由题意得:w=1.2+0.3(t﹣3)=0.3t+0.3(t≥3).
故答案为:w=0.3t+0.3(t≥3).
12.解:∵点C为AB中点,
∴BC=AC=5cm,
∴CD=BC﹣BD=3cm.
13.解:根据同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
得m+2=7
解得m=5.
故答案为5.
14.解:∵AB∥CD,
∴∠1=∠C=70°,
∴∠E=∠1﹣∠A=70°﹣25°=45°,
故答案为:45°.
15.解:(a+b)2=a2+2ab+b2=(a2+b2)+2ab=18﹣2=16,则a+b=±4;
故答案是:±4.
16.解:∵OB的方向是北偏西40°,OA的方向是北偏东20°,
∴∠AOB=40°+20°=60°,
∴∠AOD=180°﹣60°=120°,
∵OC是∠AOD的平分线,
∴∠AOC=60°,
∵20°+60°=80°,
∴射线OC的方向是北偏东80°;
故答案为:80.
17.解:(x﹣2)(y﹣2)=xy﹣2x﹣2y+4=xy﹣2(x+y)+4=﹣3,
∵x+y=2,
∴xy﹣2×2+4=﹣3,
∴xy=﹣3.
故答案为:﹣3.
18.解:∵(a+b)(a﹣b)=a2﹣b2,
∴2×(a﹣b)=6,
∴a﹣b=3.
故答案为:3.
三.解答题(共7小题,满分62分)
19.解:[(2x﹣y)2+(x﹣y)(x+y)﹣2x(x﹣2y)]÷3x
=(4x2﹣4xy+y2+x2﹣y2﹣2x2+4xy)÷3x
=3x2÷3x
=x.
20.解:(1)∵AB是直线(已知),
∴∠BOD+∠AOD=180°,
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD=×180°=30°,∠BOD=×180°=150°.
(2)∵∠BOC=∠AOD=30°,OE⊥DC,
∴∠EOC=90°,
∴∠BOE=∠EOC﹣∠BOC=90°﹣30°=60°.
21.解:(1)[(2x﹣y)(2x+y)﹣y(6x﹣y)]÷2x
=(4x2﹣y2﹣6xy+y2)÷2x
=(4x2﹣6xy)÷2x
=2x﹣3y,
当x=﹣,y=3时,原式=2×(﹣)﹣3×3=﹣10;
(2)(2x+1)2﹣x(5+2x)+(2+x)(2﹣x)
=4x2+4x+1﹣5x﹣2x2+4﹣x2
=x2﹣x+5,
当x2﹣x=5时,原式=5+5=10.
22.解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50﹣4﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
故答案为:50;
(2)在抽取调查的若干名学生中体重在C组的人数最多;D组的圆心角=×360°=72°,
故答案为:C、72;
(3)样本中体重超过60kg的学生是10+8=18人,
估计该校七年级体重超过60kg的学生大约有×1000=360人.
23.解:(1)∵(a﹣16)2+|2b﹣8|=0,
∴a﹣16=0,2b﹣8=0,
∵a、b均为非负数,
∴a=16,b=4,
(2)∵点C为线段AB的中点,AB=16,CE=4,
∴AC=AB=8,
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=AE=6,
∴CD=DE﹣CE=6﹣4=2.
24.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)
=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2
=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1
=(216﹣1)…(232+1)+1
=264﹣1+1
=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
25.(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFM=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
一.选择题(共10小题,满分30分,每小题3分)
1.下列调查方式合适的是( )
A.为了了解市民对70周年国庆大阅兵的感受,小华在某校随机采访了8名初一学生
B.为了了解全校学生用于做数学作业的时间,小民同学在网上向6位好友做了调查
C.为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式
D.为了了解“北斗导航”卫星零部件的状况,检测人员采用了普查的方式
2.下列计算正确的有( )
①3﹣1=﹣3;
②(x2)3=x5;
③x3+x3=2x3;
④(π﹣3.14)0=1.
A.1个
B.2个
C.3个
D.4个
3.从五边形的一个顶点出发可以连接的对角线条数为( )
A.1
B.2
C.3
D.4
4.石墨烯是目前世界上最薄却又最坚硬同时还是导电性能最好的纳米材料,其理论厚度大约仅0.00000034毫米.将0.00000034用科学记数法表示为( )
A.3.4×10﹣7
B.3.4×10﹣8
C.34×10﹣8
D.0.34×10﹣6
5.小亮在计算(6x3y﹣3x2y2)÷3xy时,错把括号内的减号写成了加号,那么正确结果与错误结果的乘积是( )
A.2x2﹣xy
B.2x2+xy
C.4x4﹣x2y2
D.无法计算
6.将一副三角板(∠A=30°)按如图所示方式摆放,使得AB∥EF,则∠1等于( )
A.75°
B.90°
C.105°
D.115°
7.若单项式﹣8xay和x2yb的积为﹣2x5y6,则ab的值为( )
A.2
B.30
C.﹣15
D.15
8.下列各式中,正确的有( )
A.a3+a2=a5
B.x(x
m
)3=x3m
C.a8÷a2=a4
D.(﹣2a3)2=4a6
9.如图所示的是一辆汽车行驶的速度(千米/时)与时间(分)之间的变化图,下列说法正确的是( )
A.时间是因变量,速度是自变量
B.汽车在1~3分钟时,匀速运动
C.汽车最快的速度是30千米/时
D.汽车在3~8分钟静止不动
10.如图,已知直线AB∥CD,直线EF分别与AB、CD交于点M、N,点H在直线CD上,HG⊥EF于点G,过点作GP∥AB.则下列结论:
①∠AMF与∠DNF是同旁内角;
②∠PGM=∠DNF;
③∠BMN+∠GHN=90°;
④∠AMG+∠CHG=270°.
其中正确结论的个数是( )
A.1个
B.2
个
C.3个
D.4个
二.填空题(共8小题,满分28分)
11.碚碚用新买的50元5G电话卡打长途电话,按通话时间3分钟内收1.2元,3分钟后每超过1分钟加收0.3元钱的方式缴纳话费.若通话时间为t分钟(t大于等于3分钟),那么电话费用w(元)与时间t(分钟)的关系式可以表示为
.
12.如图,点C、D在线段AB上,点C为AB中点,若AC=5cm,BD=2cm,则CD=
cm.
13.若am?a2=a7,则m的值为
.
14.如图,AB∥CD,∠A=25°,∠C=70°,则∠E=
.
15.已知a2+b2=18,ab=﹣1,则a+b=
.
16.如图,射线OA的方向是北偏东20度,射线OB的方向是北偏西40度,OD是OB的反向延长线.若OC是∠AOD的平分线,则射线OC的方向是北偏东
度.
17.已知x+y=2,且(x﹣2)(y﹣2)=﹣3,则xy的值是
.
18.若a+b=2,a2﹣b2=6,则a﹣b=
.
三.解答题(共7小题,满分62分)
19.计算:[(2x﹣y)2+(x﹣y)(x+y)﹣2x(x﹣2y)]÷3x.
20.如图,直线AB、CD相交于O,OE⊥CD,且∠BOD的度数是∠AOD的5倍.
求:(1)∠AOD、∠BOD的度数;
(2)∠BOE的度数.
21.(1)已知,y=3,求多项式[(2x﹣y)(2x+y)﹣y(6x﹣y)]÷2x的值;
(2)已知x2﹣x=5,求(2x+1)2﹣x(5+2x)+(2+x)(2﹣x)的值.
22.某校为了了解七年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5﹣46.5;B:46.5﹣53.5;C:53.5﹣60.5;D:60.5﹣67.5;E:67.5﹣74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.
请解答下列问题:
(1)这次随机抽取了
名学生调查,并补全频数分布直方图;
(2)在抽取调查的若干名学生中体重在
组的人数最多,在扇形统计图中D组的圆心角是
度;
(3)请你估计该校七年级体重超过60kg的学生大约有多少名?
23.如图,点C为线段AB的中点,点E为线段AB上的点,点D为线段AE的中点.
(1)若线段AB=a,CE=b且(a﹣16)2+|2b﹣8|=0,求a,b的值:
(2)在(1)的条件下,求线段CD的长,
24.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形
(1)请你分别表示出这两个图形中阴影部分的面积
(2)比较两图的阴影部分面积,可以得到乘法公式:
(用字母表示)
【应用】请应用这个公式完成下列各题
①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为
②计算:(2a+b﹣c)(2a﹣b+c)
【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为
②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12
25.如图,AE平分∠BAC,∠CAE=∠CEA.
(1)如图1,求证:AB∥CD;
(2)如图2,点F为线段AC上一点,连接EF,求证:∠BAF+∠AFE+∠DEF=360°;
(3)如图3,在(2)的条件下,在射线AB上取点G,连接EG,使得∠GEF=∠C,当∠AEF=35°,∠GED=2∠GEF时,求∠C的度数.
参考答案与试题解析
一.选择题(共10小题,满分30分,每小题3分)
1.解:A、为了了解市民对70周年国庆大阅兵的感受,小华在某校随机采访了8名初一学生,8名初一学生不具有代表性,调查方式不合适;
B、为了了解全校学生用于做数学作业的时间,小民同学在网上向6位好友做了调查,小民的6位好友不具有代表性,调查方式不合适;
C、为了了解全国青少年儿童的睡眠时间,统计人员采用了普查的方式,普查的意义或价值不大,应选择抽样调查,调查方式不合适;
D、为了了解“北斗导航”卫星零部件的状况,检测人员采用了普查的方式,调查方式合适;
故选:D.
2.解:①;
②(x2)3=x6;
③x3+x3=2x3;
④(π﹣3.14)0=1.
∴正确的有③④共2个.
故选:B.
3.解:∵n边形(n>3)从一个顶点出发可以引(n﹣3)条对角线,
∴从五边形的一个顶点出发可以画出5﹣3=2(条)对角线.
故选:B.
4.解:0.00000034=3.4×10﹣7.
故选:A.
5.解:正确结果为:
原式=6x3y÷3xy﹣3x2y2÷3xy
=2x2﹣xy,
错误结果为:
原式=6x3y÷3xy+3x2y2÷3xy
=2x2+xy,
∴(2x2﹣xy)(2x2+xy)=4x4﹣x2y2,
故选:C.
6.解:∵AB∥EF,
∴∠BDE=∠E=45°,
又∵∠A=30°,
∴∠B=60°,
∴∠1=∠BDE+∠B=45°+60°=105°,
故选:C.
7.解:﹣8xay×x2yb=﹣2xa+2yb+1=﹣2x5y6,
∴a+2=5,b+1=6,
解得a=3,b=5,
∴ab=3×5=15,
故选:D.
8.解:A、a3+a2,无法合并,故此选项错误;
B、x(x
m
)3=x3m+1,故此选项错误;
C、a8÷a2=a6,故此选项错误;
D、(﹣2a3)2=4a6,正确.
故选:D.
9.解:速度是因变量,时间是自变量,故选项A不合题意;
汽车在1~3分钟时,速度在增加,故选项B不合题意;
汽车最快速度是30千米/时,故选项C符合题意;
汽车在3~8分钟,匀速运动,故选项D不合题意;
故选:C.
10.解:∵∠AMF与∠DNF不是同旁内角,
∴①错误;
∵AB∥CD,GP∥AB,
∴AB∥CD∥GP,
∴∠PGM=∠CNM=∠DNF,∠BMN=∠HNG,∠AMN+∠HNG=180°,故②正确;
∵HG⊥MN,
∴∠HNG+∠GHN=90°,
∴∠BMN+∠GHN=90°,故③正确;
∵∠CHG=∠MNH+∠HGN,
∴∠MNH=∠CHG﹣90°,
∴∠AMN+∠HNG=∠AMN+∠CHG﹣90°=180°,
∴∠AMG+∠CHG=270°,故④正确,
故选:C.
二.填空题(共8小题,满分28分)
11.解:由题意得:w=1.2+0.3(t﹣3)=0.3t+0.3(t≥3).
故答案为:w=0.3t+0.3(t≥3).
12.解:∵点C为AB中点,
∴BC=AC=5cm,
∴CD=BC﹣BD=3cm.
13.解:根据同底数幂的乘法法则:
同底数幂相乘,底数不变,指数相加.
得m+2=7
解得m=5.
故答案为5.
14.解:∵AB∥CD,
∴∠1=∠C=70°,
∴∠E=∠1﹣∠A=70°﹣25°=45°,
故答案为:45°.
15.解:(a+b)2=a2+2ab+b2=(a2+b2)+2ab=18﹣2=16,则a+b=±4;
故答案是:±4.
16.解:∵OB的方向是北偏西40°,OA的方向是北偏东20°,
∴∠AOB=40°+20°=60°,
∴∠AOD=180°﹣60°=120°,
∵OC是∠AOD的平分线,
∴∠AOC=60°,
∵20°+60°=80°,
∴射线OC的方向是北偏东80°;
故答案为:80.
17.解:(x﹣2)(y﹣2)=xy﹣2x﹣2y+4=xy﹣2(x+y)+4=﹣3,
∵x+y=2,
∴xy﹣2×2+4=﹣3,
∴xy=﹣3.
故答案为:﹣3.
18.解:∵(a+b)(a﹣b)=a2﹣b2,
∴2×(a﹣b)=6,
∴a﹣b=3.
故答案为:3.
三.解答题(共7小题,满分62分)
19.解:[(2x﹣y)2+(x﹣y)(x+y)﹣2x(x﹣2y)]÷3x
=(4x2﹣4xy+y2+x2﹣y2﹣2x2+4xy)÷3x
=3x2÷3x
=x.
20.解:(1)∵AB是直线(已知),
∴∠BOD+∠AOD=180°,
∵∠BOD的度数是∠AOD的5倍,
∴∠AOD=×180°=30°,∠BOD=×180°=150°.
(2)∵∠BOC=∠AOD=30°,OE⊥DC,
∴∠EOC=90°,
∴∠BOE=∠EOC﹣∠BOC=90°﹣30°=60°.
21.解:(1)[(2x﹣y)(2x+y)﹣y(6x﹣y)]÷2x
=(4x2﹣y2﹣6xy+y2)÷2x
=(4x2﹣6xy)÷2x
=2x﹣3y,
当x=﹣,y=3时,原式=2×(﹣)﹣3×3=﹣10;
(2)(2x+1)2﹣x(5+2x)+(2+x)(2﹣x)
=4x2+4x+1﹣5x﹣2x2+4﹣x2
=x2﹣x+5,
当x2﹣x=5时,原式=5+5=10.
22.解:(1)这次抽样调查的样本容量是4÷8%=50,B组的频数=50﹣4﹣16﹣10﹣8=12,
补全频数分布直方图,如图:
故答案为:50;
(2)在抽取调查的若干名学生中体重在C组的人数最多;D组的圆心角=×360°=72°,
故答案为:C、72;
(3)样本中体重超过60kg的学生是10+8=18人,
估计该校七年级体重超过60kg的学生大约有×1000=360人.
23.解:(1)∵(a﹣16)2+|2b﹣8|=0,
∴a﹣16=0,2b﹣8=0,
∵a、b均为非负数,
∴a=16,b=4,
(2)∵点C为线段AB的中点,AB=16,CE=4,
∴AC=AB=8,
∴AE=AC+CE=12,
∵点D为线段AE的中点,
∴DE=AE=6,
∴CD=DE﹣CE=6﹣4=2.
24.解:(1)图①按照正方形面积公式可得:a2﹣b2;
图②按照长方形面积公式可得:(a+b)(a﹣b).
故答案为:a2﹣b2;(a+b)(a﹣b).
(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2
故答案为:(a+b)(a﹣b)=a2﹣b2.
【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)
∴(2m﹣n)=12÷4=3
故答案为:3.
②(2a+b﹣c)(2a﹣b+c)
=[2a+(b﹣c)][2a﹣(b﹣c)]
=4a2﹣(b﹣c)2
=4a2﹣b2+2bc﹣c2
【拓展】①
原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1
=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1
=(24﹣1)(24+1)(28+1)…(232+1)+1
=(28﹣1)(28+1)…(232+1)+1
=(216﹣1)…(232+1)+1
=264﹣1+1
=264
∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16
故答案为:6.
②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)
=100+99+98+97+…+4+3+2+1
=5050
25.(1)证明:∵AE平分∠BAC,
∴∠BAE=∠CAE,
∵∠CAE=∠CEA,
∴∠CEA=∠BAE,
∴AB∥CD;
(2)证明:过F作FM∥AB,如图,
∵AB∥CD,
∴AB∥FM∥CD,
∴∠BAF+∠AFM=180°,∠DEF+∠EFM=180°,
∴∠BAF+∠AFM+∠DEF+∠EFM=360°,
即∠BAF+∠AFE+∠DEF=360°;
(3)解:设∠GEF=∠C=x°,
∵∠GEF=∠C,∠GED=2∠GEF,
∴∠GED=2x°,
∵AB∥CD,
∴∠C+∠BAC=180°,
∴∠BAC=180°﹣x°,
∵AE平分∠BAC,
∴∠BAE=BAC=(180°﹣x°)=90°﹣x°,
由(1)知:AB∥CD,
∴∠BAE+∠AED=180°,
∵∠AEF=35°,
∴90﹣x+x﹣35+2x=180,
解得:x=50,
即∠C=50°.
同课章节目录
