2021年九年级中考数学二轮复习:因动点产生的直角三角形及平行四边形问题压轴题练习(Word版无答案)
文档属性
| 名称 | 2021年九年级中考数学二轮复习:因动点产生的直角三角形及平行四边形问题压轴题练习(Word版无答案) | 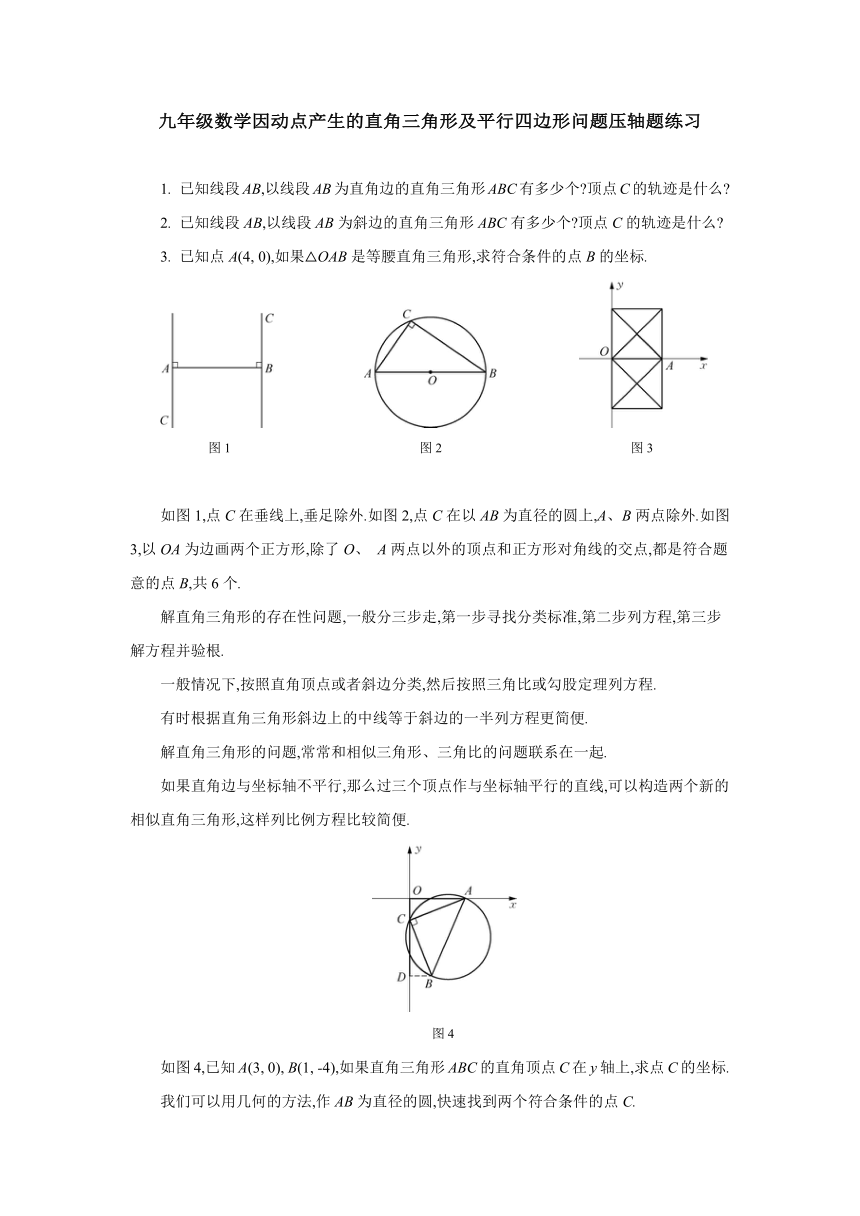 | |
| 格式 | docx | ||
| 文件大小 | 465.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 09:59:12 | ||
图片预览




文档简介
九年级数学因动点产生的直角三角形及平行四边形问题压轴题练习
1. 已知线段AB,以线段AB为直角边的直角三角形ABC有多少个?顶点C的轨迹是什么?
2. 已知线段AB,以线段AB为斜边的直角三角形ABC有多少个?顶点C的轨迹是什么?
3. 已知点A(4, 0),如果△OAB是等腰直角三角形,求符合条件的点B的坐标.
图1 图2 图3
如图1,点C在垂线上,垂足除外.如图2,点C在以AB为直径的圆上,A、 B两点除外.如图3,以OA为边画两个正方形,除了O、 A两点以外的顶点和正方形对角线的交点,都是符合题意的点B,共6个.
解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根.
一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.
有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.
解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.
如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.
图4
如图4,已知A(3, 0), B(1, -4),如果直角三角形ABC的直角顶点C在y轴上,求点C的坐标.
我们可以用几何的方法,作AB为直径的圆,快速找到两个符合条件的点C.
如果作BD⊥y轴于D,那么△AOC∽△CDB.
设OC=m,那么3m=4-m1.
这个方程有两个解,分别对应图中圆与y轴的两个交点.
1、如图,在矩形ABCO中,点O为坐标原点,点B的坐标为(4, 3),点A、 C在坐标轴上,点P在BC边上,直线l1: y=2x+3,直线l2: y=2x-3.
(1) 分别求直线l1与x轴、直线l2与AB的交点坐标;
(2) 已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3) 我们把直线l1和直线l2上的点所组成的图形称为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且点N的横坐标为x,请直接写出x的取值范围(不用说明理由).
1. 第(2)题:设M(x, 2x-3),擦去两条直线,在BC上取点P.
2. 以AP为斜边构造等腰Rt△APM,再以MA和MP为斜边构造直角三角形全等.
3. 以AP为直角边构造等腰Rt△APM,再以AP和PM为斜边构造直角三角形全等.
4. 第(3)题与(2)题相同的是∠AMP=∠ANP.求x关于m的关系式.
如图1,点A的坐标为(2, 0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A的右侧,连结BC,以BC为边在第一象限内作等边△BCD,连结AD交BC于点E.
(1) ① 直接回答:△OBC与△ABD全等吗?
② 试说明:无论点C如何移动, AD始终与OB平行;
(2) 当点C运动到使AC2=AE·AD时,如图2,经过O、 B、 C三点的抛物线y1.试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,将y1沿x轴翻折得y2,设y1与y2组成的图形为M,函数y=3x+3m的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
图1 图2
1. △CBO绕着点B逆时针旋转60°与△DBA重合,把图形中60°的角都标记出来.
2. 第(2)题要分三步完成:先确定点C,再求抛物线的解析式,最后分两种情况讨论点P,共有3个符合条件的点P.
3. 第(3)题采用数形结合思想,当直线与抛物线相切时,联立方程组消去y,那么Δ=0.
如图,已知☉O的半径长为1, AB、 AC是☉O的两条弦,且AB=AC, BO的延长线交AC于点D,连结OA、 OC.
(1) 求证:△OAD∽△ABD;
(2) 当△OCD是直角三角形时,求B、 C两点的距离;
(3) 记△AOB、 △AOD、 △COD的面积为S1、 S2、 S3,若S2是S1和S3的比例中项,求OD的长.
1. 把相等的弦所对的圆心角标记出来,由此得到的等腰三角形的底角都相等.
2. 直角三角形OCD存在两种情况,不存在∠OCD为直角的可能.
3. 第(3)题中的三个三角形都是等高三角形,把面积比转化为对应底边的比.
我们先思考三个问题:
1. 已知A、 B、 C三点,以A、 B、 C、 D为顶点的平行四边形有几个,怎么画?
2. 在坐标平面内,如何理解平行四边形ABCD的对边AB与DC平行且相等?
3. 在坐标平面内,如何理解平行四边形ABCD的对角线互相平分?
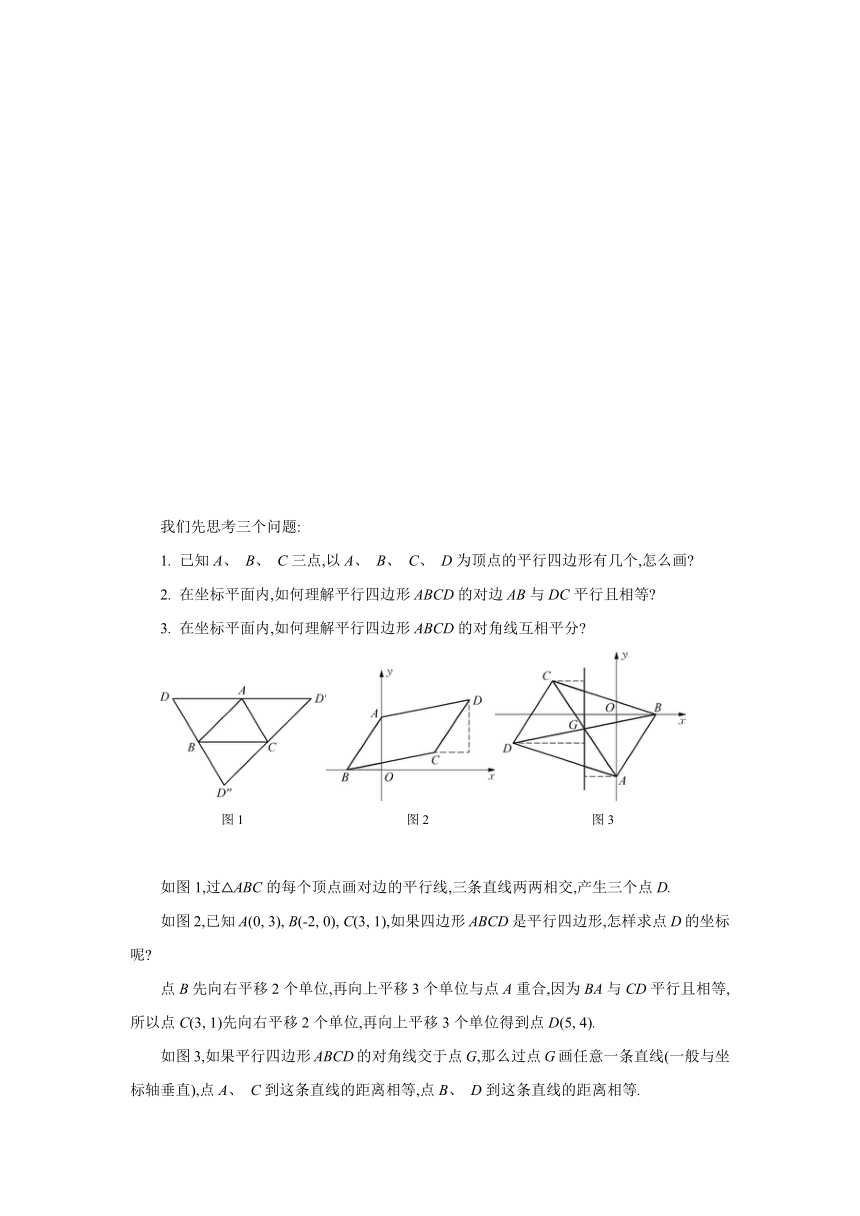
图1 图2 图3
如图1,过△ABC的每个顶点画对边的平行线,三条直线两两相交,产生三个点D.
如图2,已知A(0, 3), B(-2, 0), C(3, 1),如果四边形ABCD是平行四边形,怎样求点D的坐标呢?
点B先向右平移2个单位,再向上平移3个单位与点A重合,因为BA与CD平行且相等,所以点C(3, 1)先向右平移2个单位,再向上平移3个单位得到点D(5, 4).
如图3,如果平行四边形ABCD的对角线交于点G,那么过点G画任意一条直线(一般与坐标轴垂直),点A、 C到这条直线的距离相等,点B、 D到这条直线的距离相等.
关系式xA+xC=xB+xD和yA+yC=yB+yD有时候用起来很方便.
我们再来说说压轴题常常要用到的数形结合.
图4
如图4,点A是抛物线y=-x2+2x+3在x轴上方的一个动点, AB⊥x轴于点B,线段AB交直线y=x-1于点C,那么点A的坐标可以表示为(x, -x2+2x+3),点C的坐标可以表示为(x, x-1).
线段AB的长可以用点A的纵坐标表示为
AB=yA=-x2+2x+3,
线段AC的长可以用A、 C两点的纵坐标表示为
AC=yA-yC=-x2+2x+3-(x-1)=-x2+x+4.
通俗地说,数形结合就是: 点在图象上,可以用图象的解析式表示点的坐标,用点的坐标表示点到坐标轴的距离.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2, 9),与y轴交于点A(0, 5),与x轴交于点E、 B.
(1) 求二次函数y=ax2+bx+c的表达式;
(2) 过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3) 若点M在抛物线上,点N在其对称轴上,使得以A、 E、 N、 M为顶点的四边形是平行四边形,且AE为其一边,求点M、 N的坐标.
1. 设抛物线的顶点式比较简便.
2. 四边形APCD的对角线互相垂直,面积等于对角线积的一半.
3. 因为AE与MN平行且相等,所以M、 N两点间的水平距离、竖直距离与A、 E两点间的水平距离、竖直距离分别相等.
如图,在平面直角坐标系中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1) 求点A的坐标;
(2) 求直线AC的表达式;
(3) 点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、 B、 E、 F为顶点的四边形是菱形,直接写出点F的坐标.
请打开几何画板文件名,可以体验到,以A、 B、 E、 F为顶点的菱形存在四种情况,其中一种情况点F在x轴的下方.
1. 从待定系数的二次函数的解析式中可以得到抛物线的对称轴是直线x=1,然后这道题目和抛物线没有什么关系了.
2. 第(3)题以AB为分类标准,分两种情况讨论菱形.两种情况的菱形都可以画出准确的示意图.
如图1,在平面直角坐标系中,抛物线C: y=ax2+bx+c与x轴相交于A、 B两点,顶点为D(0, 4), AB=42.设点F(m, 0)是x轴正半轴上一点,将抛物线C绕点F旋转180°,得抛物线C'.
(1) 求抛物线C的函数表达式;
(2) 若抛物线C'与抛物线C在y轴右侧有两个不同的公共点,求m的取值范围;
(3) 如图2, P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C'上的对应点为P'.设M是C上的动点,N是C'上的动点,试探究四边形PMP'N能否成为正方形?若能,求出m的值;若不能,请说明理由.
图1 图2
1. 用m表示抛物线C'的顶点坐标,设抛物线C'的顶点式.
2. 抛物线C'与抛物线C在y轴右侧有两个不同的公共点,一个临界时刻是抛物线C'经过点D,另一个临界时刻是B、 F重合.
3. 第(3)题:先构造正方形,用m表示点M的坐标,再把点M代入抛物线C的解析式求解m的值.
如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4, 0),与过点A的直线相交于另一个点D3,52,过点D作DC⊥x轴,垂足为C.
(1) 求抛物线的表达式;
(2) 点P在线段OC上(不与点O、 C重合),过点P作PN⊥x轴,交直线AD于点M,交抛物线于点N,连结CM,求△PCM面积的最大值;
(3) 若点P是x轴正半轴上一动点,设OP的长为t,是否存在t,使以点M、 C、 D、 N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
1. 点N、 M、 P的横坐标都用t表示,点N、 M的纵坐标分别用抛物线和直线AD的解析式表示.
2. 第(2)题先求S△PCM关于t的二次函数,再求这个二次函数的最大值.
3. 第(3)题根据NM与DC相等列方程,分两种情况:N在M上方,M在N上方.
如图1,已知抛物线y=ax2+bx+c过点A(-1, 0), B(3, 0), C(0, 3).点M、 N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.
(1) 求二次函数的表达式;
(2) 过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;
(3) 若∠DMN=90°, MD=MN,求点M的横坐标.
图1 备用图
1. 设MN与抛物线的对称轴交于点H,那么MN=2MH.因此ME、 MN的长就可以用点M的坐标表示了.
2. 第(3)题中MN=MD,点M与D、 N的位置关系存在四种情况.
如图,在平面直角坐标系中,抛物线y=x2-2x-3交x轴于A、 B两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连结AC、 BC.
(1) 求曲线N所在抛物线相应的函数表达式;
(2) 求△ABC外接圆的半径;
(3) 点P为曲线M或曲线N上的一个动点,点Q为x轴上的一个动点,若以点B、 C、 P、 Q为顶点的四边形是平行四边形,求点Q的坐标.
1. 翻折以后的抛物线与x轴的交点不变,开口方向改变了,可以直接写出交点式.
2. 观察△ABC的三个顶点,发现AB边和BC边的垂直平分线都是特殊的直线,这两条直线的交点就是△ABC外接圆的圆心.
3. 第(3)题的平行四边形,以BC为分类标准,按照边或者对角线分两种情况讨论.
1. 已知线段AB,以线段AB为直角边的直角三角形ABC有多少个?顶点C的轨迹是什么?
2. 已知线段AB,以线段AB为斜边的直角三角形ABC有多少个?顶点C的轨迹是什么?
3. 已知点A(4, 0),如果△OAB是等腰直角三角形,求符合条件的点B的坐标.
图1 图2 图3
如图1,点C在垂线上,垂足除外.如图2,点C在以AB为直径的圆上,A、 B两点除外.如图3,以OA为边画两个正方形,除了O、 A两点以外的顶点和正方形对角线的交点,都是符合题意的点B,共6个.
解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根.
一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程.
有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便.
解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起.
如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便.
图4
如图4,已知A(3, 0), B(1, -4),如果直角三角形ABC的直角顶点C在y轴上,求点C的坐标.
我们可以用几何的方法,作AB为直径的圆,快速找到两个符合条件的点C.
如果作BD⊥y轴于D,那么△AOC∽△CDB.
设OC=m,那么3m=4-m1.
这个方程有两个解,分别对应图中圆与y轴的两个交点.
1、如图,在矩形ABCO中,点O为坐标原点,点B的坐标为(4, 3),点A、 C在坐标轴上,点P在BC边上,直线l1: y=2x+3,直线l2: y=2x-3.
(1) 分别求直线l1与x轴、直线l2与AB的交点坐标;
(2) 已知点M在第一象限,且是直线l2上的点,若△APM是等腰直角三角形,求点M的坐标;
(3) 我们把直线l1和直线l2上的点所组成的图形称为图形F.已知矩形ANPQ的顶点N在图形F上,Q是坐标平面内的点,且点N的横坐标为x,请直接写出x的取值范围(不用说明理由).
1. 第(2)题:设M(x, 2x-3),擦去两条直线,在BC上取点P.
2. 以AP为斜边构造等腰Rt△APM,再以MA和MP为斜边构造直角三角形全等.
3. 以AP为直角边构造等腰Rt△APM,再以AP和PM为斜边构造直角三角形全等.
4. 第(3)题与(2)题相同的是∠AMP=∠ANP.求x关于m的关系式.
如图1,点A的坐标为(2, 0),以OA为边在第一象限内作等边△OAB,点C为x轴上一动点,且在点A的右侧,连结BC,以BC为边在第一象限内作等边△BCD,连结AD交BC于点E.
(1) ① 直接回答:△OBC与△ABD全等吗?
② 试说明:无论点C如何移动, AD始终与OB平行;
(2) 当点C运动到使AC2=AE·AD时,如图2,经过O、 B、 C三点的抛物线y1.试问:y1上是否存在动点P,使△BEP为直角三角形且BE为直角边?若存在,求出点P的坐标;若不存在,请说明理由;
(3) 在(2)的条件下,将y1沿x轴翻折得y2,设y1与y2组成的图形为M,函数y=3x+3m的图象l与M有公共点.试写出:l与M的公共点为3个时,m的取值.
图1 图2
1. △CBO绕着点B逆时针旋转60°与△DBA重合,把图形中60°的角都标记出来.
2. 第(2)题要分三步完成:先确定点C,再求抛物线的解析式,最后分两种情况讨论点P,共有3个符合条件的点P.
3. 第(3)题采用数形结合思想,当直线与抛物线相切时,联立方程组消去y,那么Δ=0.
如图,已知☉O的半径长为1, AB、 AC是☉O的两条弦,且AB=AC, BO的延长线交AC于点D,连结OA、 OC.
(1) 求证:△OAD∽△ABD;
(2) 当△OCD是直角三角形时,求B、 C两点的距离;
(3) 记△AOB、 △AOD、 △COD的面积为S1、 S2、 S3,若S2是S1和S3的比例中项,求OD的长.
1. 把相等的弦所对的圆心角标记出来,由此得到的等腰三角形的底角都相等.
2. 直角三角形OCD存在两种情况,不存在∠OCD为直角的可能.
3. 第(3)题中的三个三角形都是等高三角形,把面积比转化为对应底边的比.
我们先思考三个问题:
1. 已知A、 B、 C三点,以A、 B、 C、 D为顶点的平行四边形有几个,怎么画?
2. 在坐标平面内,如何理解平行四边形ABCD的对边AB与DC平行且相等?
3. 在坐标平面内,如何理解平行四边形ABCD的对角线互相平分?
图1 图2 图3
如图1,过△ABC的每个顶点画对边的平行线,三条直线两两相交,产生三个点D.
如图2,已知A(0, 3), B(-2, 0), C(3, 1),如果四边形ABCD是平行四边形,怎样求点D的坐标呢?
点B先向右平移2个单位,再向上平移3个单位与点A重合,因为BA与CD平行且相等,所以点C(3, 1)先向右平移2个单位,再向上平移3个单位得到点D(5, 4).
如图3,如果平行四边形ABCD的对角线交于点G,那么过点G画任意一条直线(一般与坐标轴垂直),点A、 C到这条直线的距离相等,点B、 D到这条直线的距离相等.
关系式xA+xC=xB+xD和yA+yC=yB+yD有时候用起来很方便.
我们再来说说压轴题常常要用到的数形结合.
图4
如图4,点A是抛物线y=-x2+2x+3在x轴上方的一个动点, AB⊥x轴于点B,线段AB交直线y=x-1于点C,那么点A的坐标可以表示为(x, -x2+2x+3),点C的坐标可以表示为(x, x-1).
线段AB的长可以用点A的纵坐标表示为
AB=yA=-x2+2x+3,
线段AC的长可以用A、 C两点的纵坐标表示为
AC=yA-yC=-x2+2x+3-(x-1)=-x2+x+4.
通俗地说,数形结合就是: 点在图象上,可以用图象的解析式表示点的坐标,用点的坐标表示点到坐标轴的距离.
如图,在平面直角坐标系中,抛物线y=ax2+bx+c的顶点坐标为(2, 9),与y轴交于点A(0, 5),与x轴交于点E、 B.
(1) 求二次函数y=ax2+bx+c的表达式;
(2) 过点A作AC平行于x轴,交抛物线于点C,点P为抛物线上的一点(点P在AC上方),作PD平行于y轴交AB于点D,问当点P在何位置时,四边形APCD的面积最大?并求出最大面积;
(3) 若点M在抛物线上,点N在其对称轴上,使得以A、 E、 N、 M为顶点的四边形是平行四边形,且AE为其一边,求点M、 N的坐标.
1. 设抛物线的顶点式比较简便.
2. 四边形APCD的对角线互相垂直,面积等于对角线积的一半.
3. 因为AE与MN平行且相等,所以M、 N两点间的水平距离、竖直距离与A、 E两点间的水平距离、竖直距离分别相等.
如图,在平面直角坐标系中,二次函数y=x2-2x+m(m>0)的对称轴与比例系数为5的反比例函数图象交于点A,与x轴交于点B,抛物线的图象与y轴交于点C,且OC=3OB.
(1) 求点A的坐标;
(2) 求直线AC的表达式;
(3) 点E是直线AC上一动点,点F在x轴上方的平面内,且使以A、 B、 E、 F为顶点的四边形是菱形,直接写出点F的坐标.
请打开几何画板文件名,可以体验到,以A、 B、 E、 F为顶点的菱形存在四种情况,其中一种情况点F在x轴的下方.
1. 从待定系数的二次函数的解析式中可以得到抛物线的对称轴是直线x=1,然后这道题目和抛物线没有什么关系了.
2. 第(3)题以AB为分类标准,分两种情况讨论菱形.两种情况的菱形都可以画出准确的示意图.
如图1,在平面直角坐标系中,抛物线C: y=ax2+bx+c与x轴相交于A、 B两点,顶点为D(0, 4), AB=42.设点F(m, 0)是x轴正半轴上一点,将抛物线C绕点F旋转180°,得抛物线C'.
(1) 求抛物线C的函数表达式;
(2) 若抛物线C'与抛物线C在y轴右侧有两个不同的公共点,求m的取值范围;
(3) 如图2, P是第一象限内抛物线C上一点,它到两坐标轴的距离相等,点P在抛物线C'上的对应点为P'.设M是C上的动点,N是C'上的动点,试探究四边形PMP'N能否成为正方形?若能,求出m的值;若不能,请说明理由.
图1 图2
1. 用m表示抛物线C'的顶点坐标,设抛物线C'的顶点式.
2. 抛物线C'与抛物线C在y轴右侧有两个不同的公共点,一个临界时刻是抛物线C'经过点D,另一个临界时刻是B、 F重合.
3. 第(3)题:先构造正方形,用m表示点M的坐标,再把点M代入抛物线C的解析式求解m的值.
如图,在平面直角坐标系中,抛物线y=ax2+bx+1交y轴于点A,交x轴正半轴于点B(4, 0),与过点A的直线相交于另一个点D3,52,过点D作DC⊥x轴,垂足为C.
(1) 求抛物线的表达式;
(2) 点P在线段OC上(不与点O、 C重合),过点P作PN⊥x轴,交直线AD于点M,交抛物线于点N,连结CM,求△PCM面积的最大值;
(3) 若点P是x轴正半轴上一动点,设OP的长为t,是否存在t,使以点M、 C、 D、 N为顶点的四边形是平行四边形?若存在,求出t的值;若不存在,请说明理由.
1. 点N、 M、 P的横坐标都用t表示,点N、 M的纵坐标分别用抛物线和直线AD的解析式表示.
2. 第(2)题先求S△PCM关于t的二次函数,再求这个二次函数的最大值.
3. 第(3)题根据NM与DC相等列方程,分两种情况:N在M上方,M在N上方.
如图1,已知抛物线y=ax2+bx+c过点A(-1, 0), B(3, 0), C(0, 3).点M、 N为抛物线上的动点,过点M作MD∥y轴,交直线BC于点D,交x轴于点E.
(1) 求二次函数的表达式;
(2) 过点N作NF⊥x轴,垂足为点F,若四边形MNFE为正方形(此处限定点M在对称轴的右侧),求该正方形的面积;
(3) 若∠DMN=90°, MD=MN,求点M的横坐标.
图1 备用图
1. 设MN与抛物线的对称轴交于点H,那么MN=2MH.因此ME、 MN的长就可以用点M的坐标表示了.
2. 第(3)题中MN=MD,点M与D、 N的位置关系存在四种情况.
如图,在平面直角坐标系中,抛物线y=x2-2x-3交x轴于A、 B两点(点A在点B的左侧),将该抛物线位于x轴上方曲线记作M,将该抛物线位于x轴下方部分沿x轴翻折,翻折后所得曲线记作N,曲线N交y轴于点C,连结AC、 BC.
(1) 求曲线N所在抛物线相应的函数表达式;
(2) 求△ABC外接圆的半径;
(3) 点P为曲线M或曲线N上的一个动点,点Q为x轴上的一个动点,若以点B、 C、 P、 Q为顶点的四边形是平行四边形,求点Q的坐标.
1. 翻折以后的抛物线与x轴的交点不变,开口方向改变了,可以直接写出交点式.
2. 观察△ABC的三个顶点,发现AB边和BC边的垂直平分线都是特殊的直线,这两条直线的交点就是△ABC外接圆的圆心.
3. 第(3)题的平行四边形,以BC为分类标准,按照边或者对角线分两种情况讨论.
同课章节目录
