2021年中考数学二轮复习:选择、填空压轴题冲刺训练(Word版 含答案)
文档属性
| 名称 | 2021年中考数学二轮复习:选择、填空压轴题冲刺训练(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 10:02:08 | ||
图片预览




文档简介
`
中考数学选择、填空压轴题冲刺训练
题型一:选择压轴
1.立体图形展开图
⑴
美术课上,老师要求同学们将右图所示的白纸只沿虚线裁开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下列四个示意图中,只有一个符合上述要求,那么这个示意图是(
)
⑵
如图所示,E、F、G、H、M、N均为正方体棱上的中点,请在下
图中画出该正方体的展开图(标注所有的字母和线段)
⑴
B.
⑵
2.动点函数图像
⑴
如图,点是以为圆心,为直径的半圆上的动点,,设弦的长为,
的面积为,则下列图象中,能表示与的函数关系的图象大致是(
)
⑵如图,在矩形中,是对角线的中点,动点从点出发,沿方向匀
速运动到终点,动点从点出发,沿方向匀速运动到终点.已知,两
点同时出发,并同时到达终点,连接,.设运动时间为,四边形的
面积为,那么下列图象能大致刻画与之间的关系的是( )
⑶
1.如图,△是等边三角形,厘米,点从点出发,沿以每秒厘米的速度运动到点停止;同时点从点出发,沿折线以每秒厘米的速度运动到点停止.如果其中一个点停止运动,则另一个点也停止运动.设点的运动时间为秒,、两点之间的距离为厘米,则表示与的函数关系的图象大致是( )
A.
B.
C.
D.
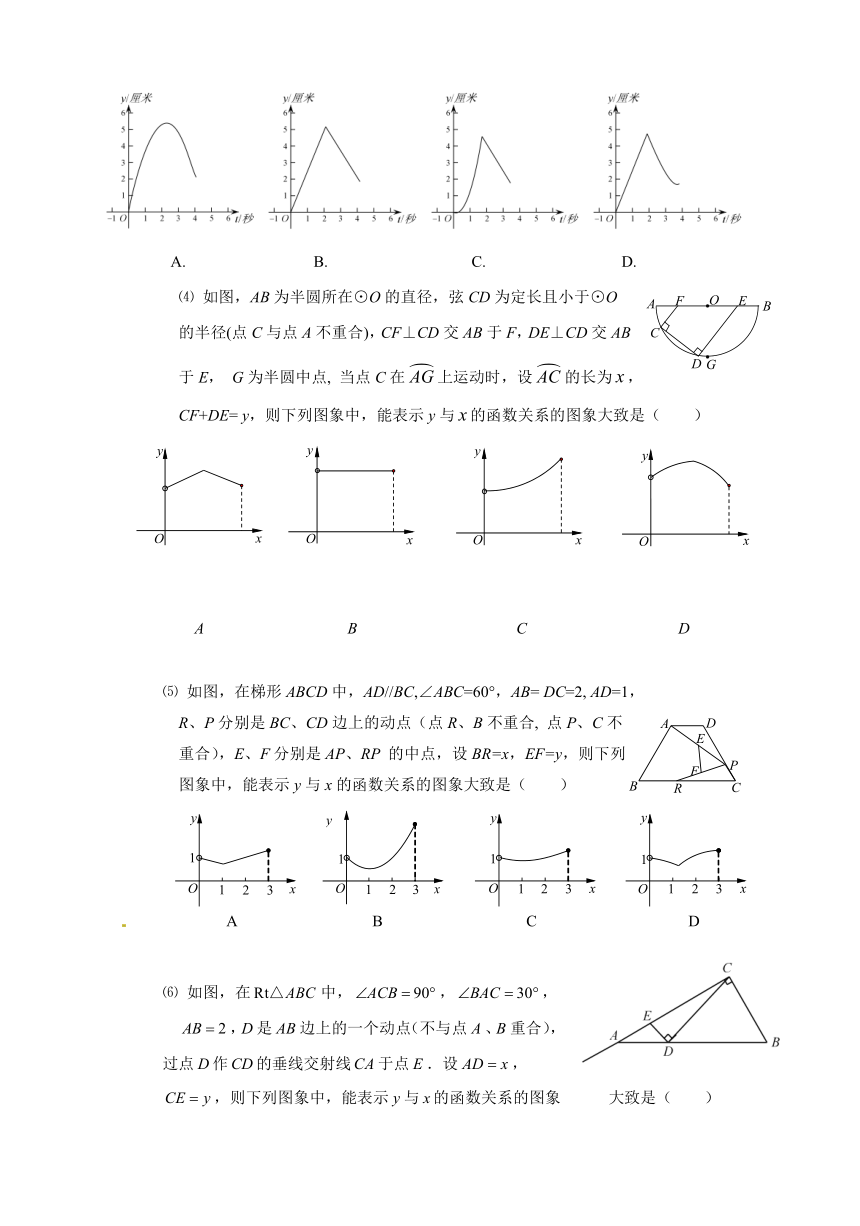
⑷
如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O
的半径(点C与点A不重合),CF⊥CD交AB于F,DE⊥CD交AB
于E,
G为半圆中点,
当点C在上运动时,设的长为,
CF+DE=
y,则下列图象中,能表示y与的函数关系的图象大致是(
)
A
B
C
D
⑸
如图,在梯形ABCD中,AD//BC,∠ABC=60°,AB=
DC=2,
AD=1,
R、P分别是BC、CD边上的动点(点R、B不重合,
点P、C不
重合),E、F分别是AP、RP
的中点,设BR=x,EF=y,则下列
图象中,能表示y与x的函数关系的图象大致是( )
A
B
C
D
⑹
如图,在中,,,
,是边上的一个动点(不与点、重合),
过点作的垂线交射线于点.设,
,则下列图象中,能表示与的函数关系的图象
大致是( )
⑴A.
⑵
A.
⑶
D.⑷B.⑸C.⑹B.
1.递进数字规律
⑴
观察下列各数,它们是按一定规律排列的,则第n个数是
.
,,,,,
⑵
观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
………………………………
请解答下列问题:
按以上规律列出第5个等式:a5
=
=
;求a1
+
a2
+
a3
+
a4
+
…
+
a100的值为
.
⑶一组按规律排列的式子:,,,,…(),其中第个式子
是
,第个式子是
(为正整数)
⑷在平面直角坐标系xOy中,动点P从原点O出发,每次向上平移1个单位长度或向
右平移2个单位长度,在上一次平移的基础上进行下一次平移.例如第1次平移后可
能到达的点是(0,1)、(2,0),第2次平移后可能到达的点是(0,2)、(2,1)、(4,
0),第3次平移后可能到达的点是(0,3)、(2,2)、(4,1)、(6,0),依此类推…….我
们记第1次平移后可能到达的所有点的横、纵坐标之和为l1,l1=3;第2次平移后可
能到达的所有点的横、纵坐标之和为l2,l2=9;第3次平移后可能到达的所有点的横、
纵坐标之和为l3,l3=18;按照这样的规律,l4=
;
ln=
(用含n的式子表示,n
是正整数).
【解析】⑴.
⑵,,.
⑶、.⑷30;.
2.递进图形规律
⑴
如图,边长为1的菱形中,,则菱形的面积是
,连结对角线,以为边作第二个菱形,使;连结,再以为边作第三个菱形,使;……,按此规律所作的第个菱形的面积为___________.
⑵如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;……;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,……,则线段D1D2的长为
,线段
Dn-1Dn
的长为
(n为正整数).
⑶
在平面直角坐标系xOy中,
正方形A1B1C1O、
A2B2C2B1、A3B3C3B2,
…,按右图所示的方
式放置.
点A1、A2、A3,
…和
B1、B2、B3,
…
分别在直线y=kx+b和x轴上.
已知C1(1,
-1),
C
2(),
则点A3的坐标是
;点An的坐标是
.
⑷
如图,已知直线:与:,过直线与轴的交点[]
作轴的垂线交于,过作轴的平行线交于,再过作轴的垂线交于,过作轴的平行线交于,……,这样一直作下去
,可在直线l1上继续得到点,,…,,….设点的横坐标为,则=
,
与的数量关系是
.
【解析】⑴,.
⑵.
.
⑶
.
⑷;.
3.循环数字规律
⑴
定义一种对正整数n的“F运算”:①当n为奇数时,结果为;②当n为偶数时,结果为(其中k是使得为奇数的正整数),并且运算重复进行.例如,取,则:
……,若,则第2次“F运算”的结果是
;若,则第2013次“F运算”的结果是
.
⑵将全体正整数排成一个三角形数阵:
1
2
3
4
5
6
7
8
9
10
.
.
.
.
.
.
.
按照以上排列的规律,第5行从左到右的第3个数为_______;第行(≥3)从左
到右的第3个数为
.(用含的代数式表示)
⑶
一列数,,,…,其中,(为不小于2的整数),则的值为
【解析】⑴1,4.
⑵13,
.
⑶.
4.循环图形规律
⑴
如图,在平面直角坐标系中,点的坐标为,
将线段绕原点O沿逆时针方向旋转,再将其延
长到,使得,得到线段;又将线段
绕原点O沿逆时针方向旋转,再将其延长到,
使得,得到线段,如此下去,得到线
段,,,则点的坐标是
,
点M5的坐标是
;若把点(是自然数)的横坐标,纵坐
标都取绝对值后得到的新坐标称之为点的绝对坐标,
则点的绝
对坐标是
(用含的代数式表示).
⑵
如图,在平面直角坐标系中,以原点O为圆心的同心圆半径由内向外依次为1,2,3,4,…,同心圆与直线和分别交于,,,
,…,则点的坐标是
.
⑶
在数学校本活动课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…
,以此类推,跳动第10次到达的顶点是
,跳动第2012次到达的顶点是
.
【解析】⑴.
⑵()
.
⑶B;C.
⑴如图3所示,△ABC内接于⊙O,∠B=90°,AB=BC,
点D是⊙O上与点B关于圆心O成中心对称的点,点P是BC边上一点,连结AD,DC,AP,已知AB=8,CP=2,
点Q是线段AP上一动点,且连结BQ并延长交四边形ABCD的一边于点R,且满足AP=BR,则的值为,则下列图象中,能表示与的函数关系的图象大致是(
)
A
B
C
D
【解析】D
⑵
如图,在平面直角坐标系中,射线是直线在第一象限的部分,圆
的圆心都在射线上且所有的圆均与轴相切,同时圆与圆外切
(为正整数),若点,则圆的半径为
【解析】
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB
上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于
点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示
y关于x的函数关系的图象大致是(
)
A.
B.
C.
D.
【解析】C
如图,矩形纸片中,.第一次将纸片折叠,使点与点重合,折痕与交于点;设的中点为,第二次将纸片折叠使点与点重合,折痕与交于点;设的中点为,第三次将纸片折叠使点与点重合,折痕与交于点,…
.按上述方法折叠,第n次折叠后的折痕交于点,则=
,=
.
第一次折叠
第二次折叠
第三次折叠
【解析】2,
某如图,在平面直角坐标系中,A1是以O为圆心,2为半径的圆与过点(0,1)且平行于x轴的直线l1的一个交点;A2是以原点O为圆心,3为半径的圆与过点(0,-2)且平行于x轴的直线l2的一个交点;A3是以原点O为圆心,4为半径的圆与过点(0,3)且平行于x轴的直线l3的一个交点;A4是以原点O为圆心,5为半径的圆与过点(0,-4)且平行于x轴的直线l4的一个交点;……,且点、、、、…都在y轴右侧,按照这样的规律进行下去,点A6的坐标为
,点An的坐标为
(用含n的式子表示,n是正整数).
【解析】(,),(,)
课后巩固
已知:如图,无盖无底的正方体纸盒,,分别为棱,上的点,且,若将这个正方体纸盒沿折线裁剪并展开,得到的平面图形是(
)
A.一个六边形
B.一个平行四边形
C.两个直角三角形
D.
一个直角三角形和一个直角梯形
【解析】B
如图:已知P是线段AB上的动点(P不与A、B重合),
分别以AP、PB为边在线段AB的同侧作等边△AEP和等
边△PFB,连结EF,设EF的中点为G;点C、D在线段
AB上且AC=BD,当点P从点C运动到点D时,
设点G到直线AB的距离为y,则能表示y与P点移动的
时间x之间函数关系的大致图象是(
)
【解析】D
⑴
一个正整数数表如下(表中下一行中数的个数是上一行中数的个数的2倍):
第1行
1
第2行
3 5
第3行
7 9 11 13
…
…
则第4行中的最后一个数是
,第行中共有
个数,
第行的第个数是
.
⑵
符号“”表示一种运算,它对一些数的运算如下:
,,,,…,
利用以上运算的规律写出
(n为正整数)
;
.
【解析】⑴
29;;
⑵
;5151
⑴
在平面直角坐标系中,正方形ABCD的位置如右图所示,
点A的坐标为(1,0),点D的坐标为(0,2).延长CB
交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于
点A2,作正方形A2B2C2C1,…按这样的规律进行下去,
第2013个正方形的面积为
.
⑵
如图,直线,点坐标为(1,0),过点作轴的垂线交直线于点,
以原点为圆心,长为半径画弧交轴于点;再过点作轴的垂线交直线于
点,以原点为圆心,长为半径画弧交轴于点,…,按此做法进行下去,
点的坐标为(
,
);点(
,
).
【解析】⑴
⑵
,
12
中考数学选择、填空压轴题冲刺训练
题型一:选择压轴
1.立体图形展开图
⑴
美术课上,老师要求同学们将右图所示的白纸只沿虚线裁开,用裁开的纸片和白纸上的阴影部分围成一个立体模型,然后放在桌面上,下列四个示意图中,只有一个符合上述要求,那么这个示意图是(
)
⑵
如图所示,E、F、G、H、M、N均为正方体棱上的中点,请在下
图中画出该正方体的展开图(标注所有的字母和线段)
⑴
B.
⑵
2.动点函数图像
⑴
如图,点是以为圆心,为直径的半圆上的动点,,设弦的长为,
的面积为,则下列图象中,能表示与的函数关系的图象大致是(
)
⑵如图,在矩形中,是对角线的中点,动点从点出发,沿方向匀
速运动到终点,动点从点出发,沿方向匀速运动到终点.已知,两
点同时出发,并同时到达终点,连接,.设运动时间为,四边形的
面积为,那么下列图象能大致刻画与之间的关系的是( )
⑶
1.如图,△是等边三角形,厘米,点从点出发,沿以每秒厘米的速度运动到点停止;同时点从点出发,沿折线以每秒厘米的速度运动到点停止.如果其中一个点停止运动,则另一个点也停止运动.设点的运动时间为秒,、两点之间的距离为厘米,则表示与的函数关系的图象大致是( )
A.
B.
C.
D.
⑷
如图,AB为半圆所在⊙O的直径,弦CD为定长且小于⊙O
的半径(点C与点A不重合),CF⊥CD交AB于F,DE⊥CD交AB
于E,
G为半圆中点,
当点C在上运动时,设的长为,
CF+DE=
y,则下列图象中,能表示y与的函数关系的图象大致是(
)
A
B
C
D
⑸
如图,在梯形ABCD中,AD//BC,∠ABC=60°,AB=
DC=2,
AD=1,
R、P分别是BC、CD边上的动点(点R、B不重合,
点P、C不
重合),E、F分别是AP、RP
的中点,设BR=x,EF=y,则下列
图象中,能表示y与x的函数关系的图象大致是( )
A
B
C
D
⑹
如图,在中,,,
,是边上的一个动点(不与点、重合),
过点作的垂线交射线于点.设,
,则下列图象中,能表示与的函数关系的图象
大致是( )
⑴A.
⑵
A.
⑶
D.⑷B.⑸C.⑹B.
1.递进数字规律
⑴
观察下列各数,它们是按一定规律排列的,则第n个数是
.
,,,,,
⑵
观察下列等式:
第1个等式:;
第2个等式:;
第3个等式:;
第4个等式:;
………………………………
请解答下列问题:
按以上规律列出第5个等式:a5
=
=
;求a1
+
a2
+
a3
+
a4
+
…
+
a100的值为
.
⑶一组按规律排列的式子:,,,,…(),其中第个式子
是
,第个式子是
(为正整数)
⑷在平面直角坐标系xOy中,动点P从原点O出发,每次向上平移1个单位长度或向
右平移2个单位长度,在上一次平移的基础上进行下一次平移.例如第1次平移后可
能到达的点是(0,1)、(2,0),第2次平移后可能到达的点是(0,2)、(2,1)、(4,
0),第3次平移后可能到达的点是(0,3)、(2,2)、(4,1)、(6,0),依此类推…….我
们记第1次平移后可能到达的所有点的横、纵坐标之和为l1,l1=3;第2次平移后可
能到达的所有点的横、纵坐标之和为l2,l2=9;第3次平移后可能到达的所有点的横、
纵坐标之和为l3,l3=18;按照这样的规律,l4=
;
ln=
(用含n的式子表示,n
是正整数).
【解析】⑴.
⑵,,.
⑶、.⑷30;.
2.递进图形规律
⑴
如图,边长为1的菱形中,,则菱形的面积是
,连结对角线,以为边作第二个菱形,使;连结,再以为边作第三个菱形,使;……,按此规律所作的第个菱形的面积为___________.
⑵如图,△ABC是一个边长为2的等边三角形,AD0⊥BC,垂足为点D0.过点D0作D0D1⊥AB,垂足为点D1;再过点D1作D1D2⊥AD0,垂足为点D2;又过点D2作D2D3⊥AB,垂足为点D3;……;这样一直作下去,得到一组线段:D0D1,D1D2,D2D3,……,则线段D1D2的长为
,线段
Dn-1Dn
的长为
(n为正整数).
⑶
在平面直角坐标系xOy中,
正方形A1B1C1O、
A2B2C2B1、A3B3C3B2,
…,按右图所示的方
式放置.
点A1、A2、A3,
…和
B1、B2、B3,
…
分别在直线y=kx+b和x轴上.
已知C1(1,
-1),
C
2(),
则点A3的坐标是
;点An的坐标是
.
⑷
如图,已知直线:与:,过直线与轴的交点[]
作轴的垂线交于,过作轴的平行线交于,再过作轴的垂线交于,过作轴的平行线交于,……,这样一直作下去
,可在直线l1上继续得到点,,…,,….设点的横坐标为,则=
,
与的数量关系是
.
【解析】⑴,.
⑵.
.
⑶
.
⑷;.
3.循环数字规律
⑴
定义一种对正整数n的“F运算”:①当n为奇数时,结果为;②当n为偶数时,结果为(其中k是使得为奇数的正整数),并且运算重复进行.例如,取,则:
……,若,则第2次“F运算”的结果是
;若,则第2013次“F运算”的结果是
.
⑵将全体正整数排成一个三角形数阵:
1
2
3
4
5
6
7
8
9
10
.
.
.
.
.
.
.
按照以上排列的规律,第5行从左到右的第3个数为_______;第行(≥3)从左
到右的第3个数为
.(用含的代数式表示)
⑶
一列数,,,…,其中,(为不小于2的整数),则的值为
【解析】⑴1,4.
⑵13,
.
⑶.
4.循环图形规律
⑴
如图,在平面直角坐标系中,点的坐标为,
将线段绕原点O沿逆时针方向旋转,再将其延
长到,使得,得到线段;又将线段
绕原点O沿逆时针方向旋转,再将其延长到,
使得,得到线段,如此下去,得到线
段,,,则点的坐标是
,
点M5的坐标是
;若把点(是自然数)的横坐标,纵坐
标都取绝对值后得到的新坐标称之为点的绝对坐标,
则点的绝
对坐标是
(用含的代数式表示).
⑵
如图,在平面直角坐标系中,以原点O为圆心的同心圆半径由内向外依次为1,2,3,4,…,同心圆与直线和分别交于,,,
,…,则点的坐标是
.
⑶
在数学校本活动课上,张老师设计了一个游戏,让电动娃娃在边长为1的正方形的四个顶点上依次跳动.规定:从顶点A出发,每跳动一步的长均为1.第一次顺时针方向跳1步到达顶点D,第二次逆时针方向跳2步到达顶点B,第三次顺时针方向跳3步到达顶点C,第四次逆时针方向跳4步到达顶点C,…
,以此类推,跳动第10次到达的顶点是
,跳动第2012次到达的顶点是
.
【解析】⑴.
⑵()
.
⑶B;C.
⑴如图3所示,△ABC内接于⊙O,∠B=90°,AB=BC,
点D是⊙O上与点B关于圆心O成中心对称的点,点P是BC边上一点,连结AD,DC,AP,已知AB=8,CP=2,
点Q是线段AP上一动点,且连结BQ并延长交四边形ABCD的一边于点R,且满足AP=BR,则的值为,则下列图象中,能表示与的函数关系的图象大致是(
)
A
B
C
D
【解析】D
⑵
如图,在平面直角坐标系中,射线是直线在第一象限的部分,圆
的圆心都在射线上且所有的圆均与轴相切,同时圆与圆外切
(为正整数),若点,则圆的半径为
【解析】
如图,Rt△ABC中,∠C=90°,AC=3,BC=4,P是斜边AB
上一动点(不与点A、B重合),PQ⊥AB交△ABC的直角边于
点Q,设AP为x,△APQ的面积为y,则下列图象中,能表示
y关于x的函数关系的图象大致是(
)
A.
B.
C.
D.
【解析】C
如图,矩形纸片中,.第一次将纸片折叠,使点与点重合,折痕与交于点;设的中点为,第二次将纸片折叠使点与点重合,折痕与交于点;设的中点为,第三次将纸片折叠使点与点重合,折痕与交于点,…
.按上述方法折叠,第n次折叠后的折痕交于点,则=
,=
.
第一次折叠
第二次折叠
第三次折叠
【解析】2,
某如图,在平面直角坐标系中,A1是以O为圆心,2为半径的圆与过点(0,1)且平行于x轴的直线l1的一个交点;A2是以原点O为圆心,3为半径的圆与过点(0,-2)且平行于x轴的直线l2的一个交点;A3是以原点O为圆心,4为半径的圆与过点(0,3)且平行于x轴的直线l3的一个交点;A4是以原点O为圆心,5为半径的圆与过点(0,-4)且平行于x轴的直线l4的一个交点;……,且点、、、、…都在y轴右侧,按照这样的规律进行下去,点A6的坐标为
,点An的坐标为
(用含n的式子表示,n是正整数).
【解析】(,),(,)
课后巩固
已知:如图,无盖无底的正方体纸盒,,分别为棱,上的点,且,若将这个正方体纸盒沿折线裁剪并展开,得到的平面图形是(
)
A.一个六边形
B.一个平行四边形
C.两个直角三角形
D.
一个直角三角形和一个直角梯形
【解析】B
如图:已知P是线段AB上的动点(P不与A、B重合),
分别以AP、PB为边在线段AB的同侧作等边△AEP和等
边△PFB,连结EF,设EF的中点为G;点C、D在线段
AB上且AC=BD,当点P从点C运动到点D时,
设点G到直线AB的距离为y,则能表示y与P点移动的
时间x之间函数关系的大致图象是(
)
【解析】D
⑴
一个正整数数表如下(表中下一行中数的个数是上一行中数的个数的2倍):
第1行
1
第2行
3 5
第3行
7 9 11 13
…
…
则第4行中的最后一个数是
,第行中共有
个数,
第行的第个数是
.
⑵
符号“”表示一种运算,它对一些数的运算如下:
,,,,…,
利用以上运算的规律写出
(n为正整数)
;
.
【解析】⑴
29;;
⑵
;5151
⑴
在平面直角坐标系中,正方形ABCD的位置如右图所示,
点A的坐标为(1,0),点D的坐标为(0,2).延长CB
交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于
点A2,作正方形A2B2C2C1,…按这样的规律进行下去,
第2013个正方形的面积为
.
⑵
如图,直线,点坐标为(1,0),过点作轴的垂线交直线于点,
以原点为圆心,长为半径画弧交轴于点;再过点作轴的垂线交直线于
点,以原点为圆心,长为半径画弧交轴于点,…,按此做法进行下去,
点的坐标为(
,
);点(
,
).
【解析】⑴
⑵
,
12
同课章节目录
