2020-2021学年人教版(2019)选择性必修第一册 4.1光的折射 课件(18张PPT)
文档属性
| 名称 | 2020-2021学年人教版(2019)选择性必修第一册 4.1光的折射 课件(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 573.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-05-27 05:26:03 | ||
图片预览



文档简介
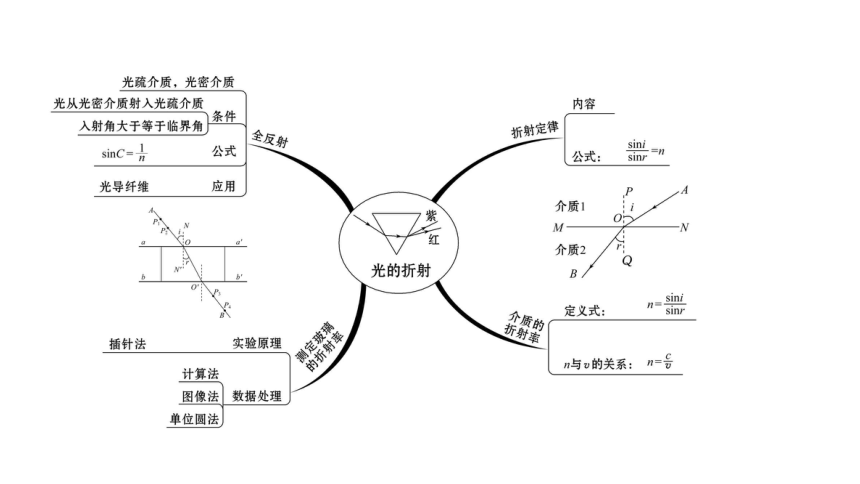
光的折射
知识体系?思维导图
考点整合?素养提升
【核心素养-物理观念】
考 点 反射定律、折射定律和折射率
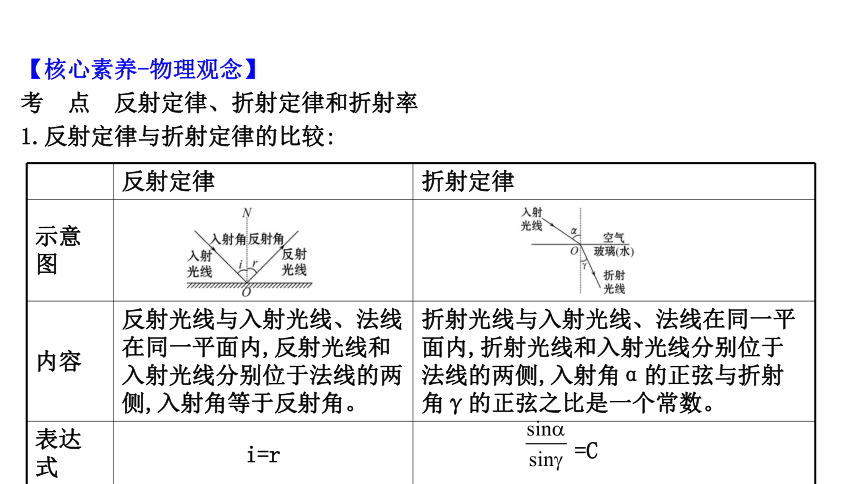
1.反射定律与折射定律的比较:
反射定律
折射定律
示意图
内容
反射光线与入射光线、法线在同一平面内,反射光线和入射光线分别位于法线的两侧,入射角等于反射角。
折射光线与入射光线、法线在同一平面内,折射光线和入射光线分别位于法线的两侧,入射角α的正弦与折射角γ的正弦之比是一个常数。
表达式
i=r
=C
2.折射率的两种表述:
(1)光从真空进入某种介质发生折射时,入射角α的正弦跟折射角γ的正弦之比等于这种介质的折射率n,即 。
(2)某种介质的折射率n亦等于光在真空中的速度c跟光在介质中的速度v之比,即n= 。
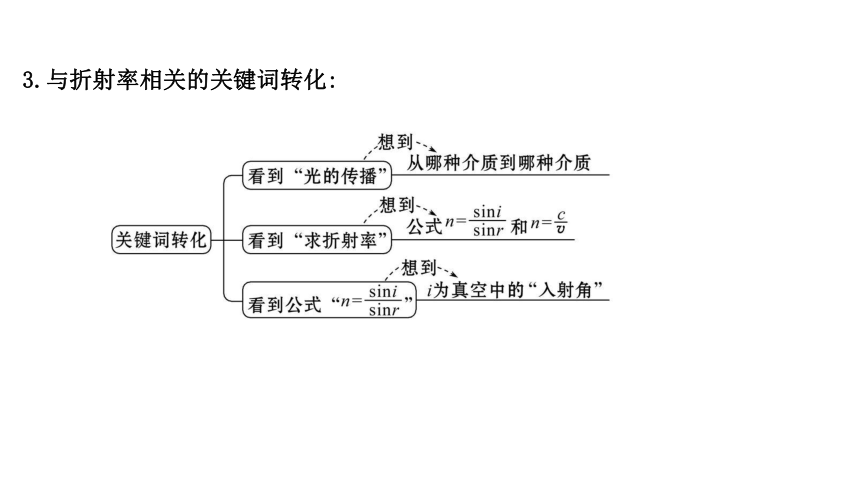
3.与折射率相关的关键词转化:
【典例】
(2020·全国Ⅱ卷)直角棱镜的折射率n=1.5,其横截面如图所示,
图中∠C=90°,∠A=30°。截面内一细束与BC边平行的光线,从
棱镜AB边上的D点射入,经折射后射到BC边上。
(1)光线在BC边上是否会发生全反射?说明理由;
(2)不考虑多次反射,求从AC边射出的光线与最初的入射光线夹角的正弦值。
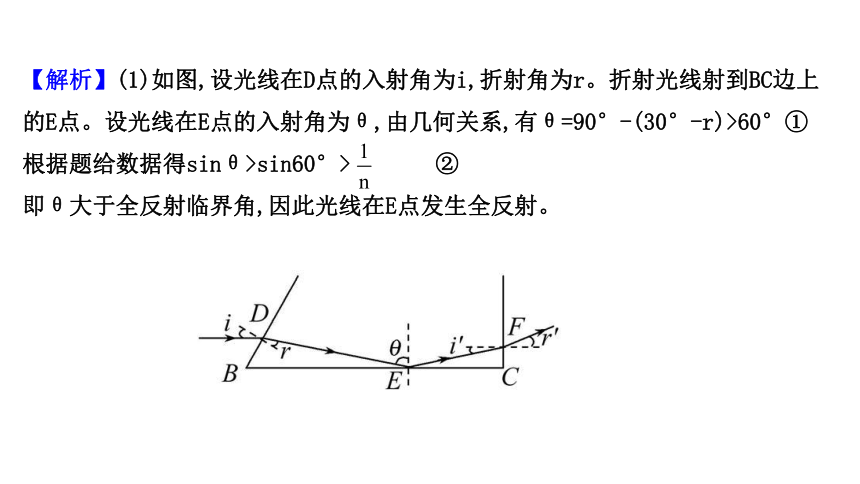
【解析】(1)如图,设光线在D点的入射角为i,折射角为r。折射光线射到BC边上的E点。设光线在E点的入射角为θ,由几何关系,有θ=90°-(30°-r)>60°①
根据题给数据得sinθ>sin60°> ②
即θ大于全反射临界角,因此光线在E点发生全反射。
(2)设光线在AC边上的F点射出棱镜,光线的入射角为i′,折射角为r′,由几何关系、反射定律及折射定律,有i=30°③
i′=90°-θ ④
sin i=nsinr ⑤
nsini′=sinr′ ⑥
联立①③④⑤⑥式并代入题给数据,得
⑦
由几何关系,r′即AC边射出的光线与最初的入射光线的夹角。
答案:(1)能 原因见解析 (2)
【素养评价】
如图,置于空气中的直角三棱镜ABC,折射率为 、AB长为2a。一束光线以45°的入射角射至AB边的中点。设空气中的光速为c,求:光线进入棱镜到从AC边射出所经历的时间。
【解析】由 ,已知:i=45°,n= ,
得:r=30°。
所以光线在三棱镜中平行BC传播且垂直AC射出,如图,由几何关系可知,光线在三棱镜中传播的距离s= ,
设光在三棱镜内的速度为v,则:v= ,
又s=vt得:
答案:
【核心素养-科学思维】
考 点 分析光路控制问题
平行玻璃砖、三棱镜和圆柱体(球)对光路的控制:
类别
项目
平行玻璃砖
三棱镜
圆柱体(球)
结构
玻璃砖上下表面是平行的
横截面为三角形
横截面是圆
对光线
的作用
通过平行玻璃砖的光
线不改变传播方向,但要发生侧移
通过三棱镜的光线经两
次折射后,出射光线向棱镜底边偏折
圆界面的法线是过圆心
的直线,经过两次折射后向圆心偏折
应用
测定玻璃的折射率
全反射棱镜,改变光的传播方向
改变光的传播方向
提醒:不同颜色的光的频率不同,在同一种介质中的折射率、光速也不同,发生全反射现象的临界角也不同。
【典例】(2020·成都高二检测)如图所示为一个均匀透明介质球,球心位于O点,半径为R,一束单色光从真空中沿DC方向平行于直径AOB射到介质球上的C点,DC与AB的距离H= R,若该光束射入球体经一次反射后由P点(图中未标出)再次折射向真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c。求:
(1)介质球的折射率和光束从C点射入到从P点射出所经历的总时间;
(2)射入球体内的光线有可能发生全反射吗?
【解析】(1)作出光路如图,
光线经反射后到达介质与空气的界面时,出射角i′=i,由折射定律可得r′=r
折射光线PQ与入射光线DC平行,则∠POA=∠COA=i,i=60°,折射角r=30°,
折射率
光从C射入到射出通过的路程是s=4Rcos30° ,光在介质球中的传播速度
v=
则该光从C射入到射出的总时间t= =
(2)由n= 可知,sinC=
由图知θ=r′=30°答案:(1) (2)不会发生全反射
【素养评价】
如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m。从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为 。
(1)求池内的水深。
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接收的光线与竖直方向的夹角恰好为45°。求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
【解析】(1)如图,设到达池边的光线的入射角为i。依题意,水的折射率n= ,光线的折射角θ=90°。由折射定律有
nsini=sinθ ①
由几何关系有
②
式中,l=3 m,h是池内水的深度。联立①②式并代入题给数据得h= m≈2.6 m③
(2)设此时救生员的眼睛到池边的距离为x。依题意,救生员的视线与竖直方向的夹角为θ′=45°。由折射定律有
nsini′=sinθ′ ④
式中,i′是光线在水面的入射角。设池底点光源A到水面入射点的水平距离为a。由几何关系有
⑤
x+l=a+h′ ⑥
式中h′=2 m。联立各式得
x=(3 -1) m≈0.7 m
答案:(1)2.6 m (2)0.7 m
知识体系?思维导图
考点整合?素养提升
【核心素养-物理观念】
考 点 反射定律、折射定律和折射率
1.反射定律与折射定律的比较:
反射定律
折射定律
示意图
内容
反射光线与入射光线、法线在同一平面内,反射光线和入射光线分别位于法线的两侧,入射角等于反射角。
折射光线与入射光线、法线在同一平面内,折射光线和入射光线分别位于法线的两侧,入射角α的正弦与折射角γ的正弦之比是一个常数。
表达式
i=r
=C
2.折射率的两种表述:
(1)光从真空进入某种介质发生折射时,入射角α的正弦跟折射角γ的正弦之比等于这种介质的折射率n,即 。
(2)某种介质的折射率n亦等于光在真空中的速度c跟光在介质中的速度v之比,即n= 。
3.与折射率相关的关键词转化:
【典例】
(2020·全国Ⅱ卷)直角棱镜的折射率n=1.5,其横截面如图所示,
图中∠C=90°,∠A=30°。截面内一细束与BC边平行的光线,从
棱镜AB边上的D点射入,经折射后射到BC边上。
(1)光线在BC边上是否会发生全反射?说明理由;
(2)不考虑多次反射,求从AC边射出的光线与最初的入射光线夹角的正弦值。
【解析】(1)如图,设光线在D点的入射角为i,折射角为r。折射光线射到BC边上的E点。设光线在E点的入射角为θ,由几何关系,有θ=90°-(30°-r)>60°①
根据题给数据得sinθ>sin60°> ②
即θ大于全反射临界角,因此光线在E点发生全反射。
(2)设光线在AC边上的F点射出棱镜,光线的入射角为i′,折射角为r′,由几何关系、反射定律及折射定律,有i=30°③
i′=90°-θ ④
sin i=nsinr ⑤
nsini′=sinr′ ⑥
联立①③④⑤⑥式并代入题给数据,得
⑦
由几何关系,r′即AC边射出的光线与最初的入射光线的夹角。
答案:(1)能 原因见解析 (2)
【素养评价】
如图,置于空气中的直角三棱镜ABC,折射率为 、AB长为2a。一束光线以45°的入射角射至AB边的中点。设空气中的光速为c,求:光线进入棱镜到从AC边射出所经历的时间。
【解析】由 ,已知:i=45°,n= ,
得:r=30°。
所以光线在三棱镜中平行BC传播且垂直AC射出,如图,由几何关系可知,光线在三棱镜中传播的距离s= ,
设光在三棱镜内的速度为v,则:v= ,
又s=vt得:
答案:
【核心素养-科学思维】
考 点 分析光路控制问题
平行玻璃砖、三棱镜和圆柱体(球)对光路的控制:
类别
项目
平行玻璃砖
三棱镜
圆柱体(球)
结构
玻璃砖上下表面是平行的
横截面为三角形
横截面是圆
对光线
的作用
通过平行玻璃砖的光
线不改变传播方向,但要发生侧移
通过三棱镜的光线经两
次折射后,出射光线向棱镜底边偏折
圆界面的法线是过圆心
的直线,经过两次折射后向圆心偏折
应用
测定玻璃的折射率
全反射棱镜,改变光的传播方向
改变光的传播方向
提醒:不同颜色的光的频率不同,在同一种介质中的折射率、光速也不同,发生全反射现象的临界角也不同。
【典例】(2020·成都高二检测)如图所示为一个均匀透明介质球,球心位于O点,半径为R,一束单色光从真空中沿DC方向平行于直径AOB射到介质球上的C点,DC与AB的距离H= R,若该光束射入球体经一次反射后由P点(图中未标出)再次折射向真空中,此时的出射光线刚好与入射光线平行,已知光在真空中的速度为c。求:
(1)介质球的折射率和光束从C点射入到从P点射出所经历的总时间;
(2)射入球体内的光线有可能发生全反射吗?
【解析】(1)作出光路如图,
光线经反射后到达介质与空气的界面时,出射角i′=i,由折射定律可得r′=r
折射光线PQ与入射光线DC平行,则∠POA=∠COA=i,i=60°,折射角r=30°,
折射率
光从C射入到射出通过的路程是s=4Rcos30° ,光在介质球中的传播速度
v=
则该光从C射入到射出的总时间t= =
(2)由n= 可知,sinC=
由图知θ=r′=30°
【素养评价】
如图,在注满水的游泳池的池底有一点光源A,它到池边的水平距离为3.0 m。从点光源A射向池边的光线AB与竖直方向的夹角恰好等于全反射的临界角,水的折射率为 。
(1)求池内的水深。
(2)一救生员坐在离池边不远处的高凳上,他的眼睛到池面的高度为2.0 m。当他看到正前下方的点光源A时,他的眼睛所接收的光线与竖直方向的夹角恰好为45°。求救生员的眼睛到池边的水平距离(结果保留1位有效数字)。
【解析】(1)如图,设到达池边的光线的入射角为i。依题意,水的折射率n= ,光线的折射角θ=90°。由折射定律有
nsini=sinθ ①
由几何关系有
②
式中,l=3 m,h是池内水的深度。联立①②式并代入题给数据得h= m≈2.6 m③
(2)设此时救生员的眼睛到池边的距离为x。依题意,救生员的视线与竖直方向的夹角为θ′=45°。由折射定律有
nsini′=sinθ′ ④
式中,i′是光线在水面的入射角。设池底点光源A到水面入射点的水平距离为a。由几何关系有
⑤
x+l=a+h′ ⑥
式中h′=2 m。联立各式得
x=(3 -1) m≈0.7 m
答案:(1)2.6 m (2)0.7 m
