青岛版数学九年级上册第四章第六节圆与圆的位置关系授课课件
文档属性
| 名称 | 青岛版数学九年级上册第四章第六节圆与圆的位置关系授课课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-29 06:50:38 | ||
图片预览




文档简介
(共34张PPT)
4.6 圆与圆的位置关系
青岛版数学九年级上册第四章第六节 圆与圆的位置关系
东平县州城街道第二中学 崔兴彬
一、预习反馈
二、复习引入
三、合作探究
四、互动拓展
五、展示交流
六、达标检测
七、课堂小结
课前预习
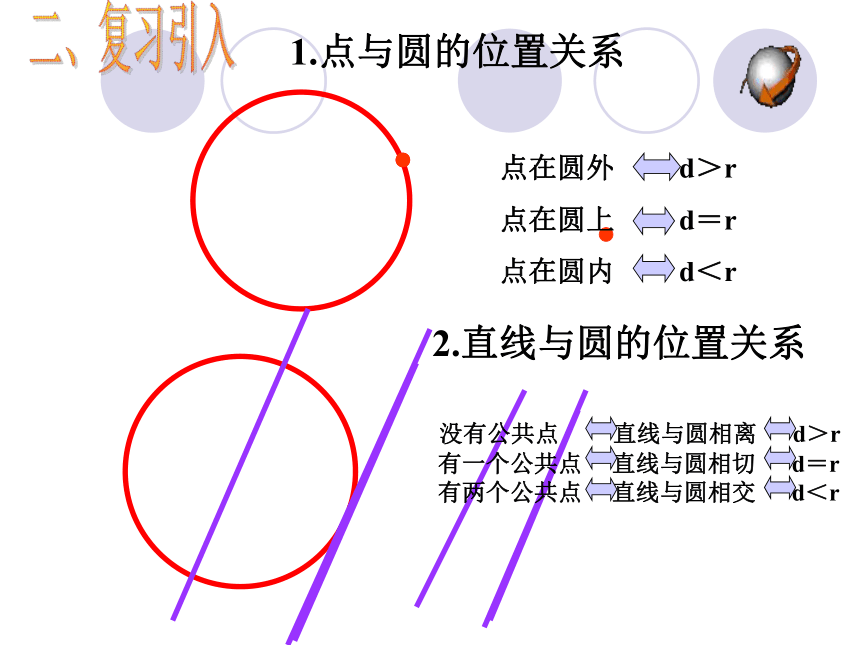
1.点与圆的位置关系
2.直线与圆的位置关系
点在圆外 d>r
点在圆上 d=r
点在圆内 d<r
没有公共点 直线与圆相离 d>r
有一个公共点 直线与圆相切 d=r
有两个公共点 直线与圆相交 d<r
1.经历探索圆与圆的位置关系的过程,了解圆与圆的位置关系。
2.能利用圆心距d、半径R和r的关系判定圆与圆的位置关系。
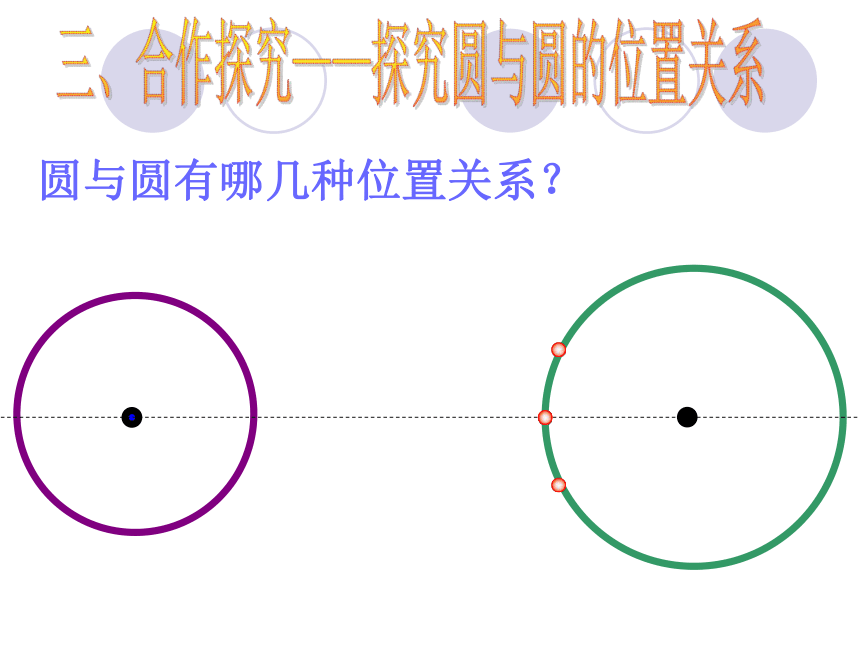
圆与圆有哪几种位置关系?
外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离.
外切:两圆有一个公共点,并且除了公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.
切点
切点
相交:两圆有两个公共点时,叫两圆相交.
内切:两圆有一个公共点,并且除了公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切.
内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含.
特 例
同心圆
圆
和
圆
的
位
置
关
系
外 离
内切
相交
外切
内含
没有公共点
相 离
一个公共点
相切
两个公共点
相 交
圆与圆的位置关系(交点个数)
圆心距:两圆圆心之间的距离
1.⊙A和⊙B外离
d>r1+r2
A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
2.⊙A和⊙B外切
d=r1+r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
r1-r23.⊙A和⊙B相交
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
4.⊙A和⊙B内切
d=r1-r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
5.⊙A和⊙B内含
dA
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
两圆的半径和圆心距数量关系与圆的位置关系
1.⊙A和⊙B外离
d>r1+r2
2.⊙A和⊙B外切
d=r1+r2
3.⊙A和⊙B相交
r1-r24.⊙A和⊙B内切
5.⊙A和⊙B内含
d=r1-r2
d例1 如图,⊙O的半径为5 cm,点P是⊙O外一点,OP=8 cm.以P点为圆心作⊙P与⊙O相切, 则⊙P的半径是多少
解:(1)设⊙O与⊙P外切于点A,
则 PA=OP-OA
所以PA=3 cm,
(2)设⊙O与⊙P内切于点B,
则 PB=PO+OB
所以PB=13 cm.
A
B
P
O
例2 已知两圆半径分别为3和4,圆心的坐标分别是(0,3)和(4,0),试判断这两圆的位置关系.
y
x
1、举出一些能表示两个圆不同位置关系的实例。
2、 ⊙O1和⊙O2的半径分别为3厘米和4厘米,设
(1) O1O2=8厘米; (2) O1O2=7厘米;
(3) O1O2=5厘米; (4) O1O2=1厘米;
(5) O1O2=0.5厘米; (6) O1和O2重合。
⊙O1和⊙O2的位置关系怎样?
(1)外离 (2)外切
(3)相交 (4)内切
(5)内含 (6)同心圆
4. ⊙01和⊙02 的半径分别为3cm 和 5 cm ,
当0102= 8cm时,两圆的位置关是 .
当0102= 2cm时,两圆的位置关是 .
当0102= 10cm时,两圆的位置关是 .
3. 两圆有两个交点,则两圆的位置关系是 .
两圆没有交点,则两圆的位置关系是 .
两圆只有一个交点,则两圆的位置关系是 .
5. 当两圆外切, 0102= 10,r1=4时,r2= .
当两圆内切, 0102= 2,r1=5时,r2 = .
6.定圆⊙O半径为3cm,动圆⊙P半径为1cm.
当两圆 时,OP为 cm?点P可以在什么样的线上运动?
O
P
外切
内切
当两圆相切时,OP为多少?
两个等圆有那几种位置关系?
(外离.外切.相交.重合)
动脑筋
完成导学案《达标检测》
相信你能行!
1.圆与圆的位置关系(从公共点个数看)
(没有公共点)
(有1个公共点)
(有2个公共点)
相离
外离
内含
特殊情况
同心圆
相切
外切
内切
相交
圆与圆的五种位置关系
相交
位置关系 d 和R、 r关系 交点
两圆外离 d >R+ r 0
两圆外切 d =R+ r 1
两圆相交 R r两圆内切 d = R r 1
两圆内含 0≤ dr) 0
性质
判定
2.两圆位置关系的性质与判定:
教师寄语
要养成用数学的思维去解读世界,用数学的语言去说明道理的习惯.
下课了!
4.6 圆与圆的位置关系
青岛版数学九年级上册第四章第六节 圆与圆的位置关系
东平县州城街道第二中学 崔兴彬
一、预习反馈
二、复习引入
三、合作探究
四、互动拓展
五、展示交流
六、达标检测
七、课堂小结
课前预习
1.点与圆的位置关系
2.直线与圆的位置关系
点在圆外 d>r
点在圆上 d=r
点在圆内 d<r
没有公共点 直线与圆相离 d>r
有一个公共点 直线与圆相切 d=r
有两个公共点 直线与圆相交 d<r
1.经历探索圆与圆的位置关系的过程,了解圆与圆的位置关系。
2.能利用圆心距d、半径R和r的关系判定圆与圆的位置关系。
圆与圆有哪几种位置关系?
外离:两圆无公共点,并且每个圆上的点都在另一个圆的外部时,叫两圆外离.
外切:两圆有一个公共点,并且除了公共点外,每个圆上的点都在另一个圆的外部时,叫两圆外切.
切点
切点
相交:两圆有两个公共点时,叫两圆相交.
内切:两圆有一个公共点,并且除了公共点外,一个圆上的点都在另一个圆的内部时,叫两圆内切.
内含:两圆无公共点,并且一个圆上的点都在另一个圆的内部时,叫两圆内含.
特 例
同心圆
圆
和
圆
的
位
置
关
系
外 离
内切
相交
外切
内含
没有公共点
相 离
一个公共点
相切
两个公共点
相 交
圆与圆的位置关系(交点个数)
圆心距:两圆圆心之间的距离
1.⊙A和⊙B外离
d>r1+r2
A
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
2.⊙A和⊙B外切
d=r1+r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
r1-r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
A
B
4.⊙A和⊙B内切
d=r1-r2
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
5.⊙A和⊙B内含
d
B
设⊙A的半径为r1,⊙B的半径为r2,圆心距为d
两圆的半径和圆心距数量关系与圆的位置关系
1.⊙A和⊙B外离
d>r1+r2
2.⊙A和⊙B外切
d=r1+r2
3.⊙A和⊙B相交
r1-r2
5.⊙A和⊙B内含
d=r1-r2
d
解:(1)设⊙O与⊙P外切于点A,
则 PA=OP-OA
所以PA=3 cm,
(2)设⊙O与⊙P内切于点B,
则 PB=PO+OB
所以PB=13 cm.
A
B
P
O
例2 已知两圆半径分别为3和4,圆心的坐标分别是(0,3)和(4,0),试判断这两圆的位置关系.
y
x
1、举出一些能表示两个圆不同位置关系的实例。
2、 ⊙O1和⊙O2的半径分别为3厘米和4厘米,设
(1) O1O2=8厘米; (2) O1O2=7厘米;
(3) O1O2=5厘米; (4) O1O2=1厘米;
(5) O1O2=0.5厘米; (6) O1和O2重合。
⊙O1和⊙O2的位置关系怎样?
(1)外离 (2)外切
(3)相交 (4)内切
(5)内含 (6)同心圆
4. ⊙01和⊙02 的半径分别为3cm 和 5 cm ,
当0102= 8cm时,两圆的位置关是 .
当0102= 2cm时,两圆的位置关是 .
当0102= 10cm时,两圆的位置关是 .
3. 两圆有两个交点,则两圆的位置关系是 .
两圆没有交点,则两圆的位置关系是 .
两圆只有一个交点,则两圆的位置关系是 .
5. 当两圆外切, 0102= 10,r1=4时,r2= .
当两圆内切, 0102= 2,r1=5时,r2 = .
6.定圆⊙O半径为3cm,动圆⊙P半径为1cm.
当两圆 时,OP为 cm?点P可以在什么样的线上运动?
O
P
外切
内切
当两圆相切时,OP为多少?
两个等圆有那几种位置关系?
(外离.外切.相交.重合)
动脑筋
完成导学案《达标检测》
相信你能行!
1.圆与圆的位置关系(从公共点个数看)
(没有公共点)
(有1个公共点)
(有2个公共点)
相离
外离
内含
特殊情况
同心圆
相切
外切
内切
相交
圆与圆的五种位置关系
相交
位置关系 d 和R、 r关系 交点
两圆外离 d >R+ r 0
两圆外切 d =R+ r 1
两圆相交 R r
两圆内含 0≤ d
性质
判定
2.两圆位置关系的性质与判定:
教师寄语
要养成用数学的思维去解读世界,用数学的语言去说明道理的习惯.
下课了!
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
