1.6有理数的乘法课件

(共26张PPT)
教材背景分析
在此之前，学生已经学习了非负整
数乘法以及有理数的加减法运算，这
为学生学习本节课打下了良好的基础，
本节课，也为学生学习有理数的除法
和有理数的乘方做铺垫，可以说，本
节内容，是数学知识的“桥梁”。
教学目标设计
知识目标：理解有理数乘法的意义，掌握有理数乘法法则，能正确进行计算。
难点：有理数乘法的意义。
重点：有理数的乘法法则。
能力目标：渗透分类，化归等数学思想方法，培养学生观察，分析，运算等能力。
情感目标：让学生经历有理数乘法法则的探究过程，激发学生的求知欲望，培养学生乐于探索的精神。
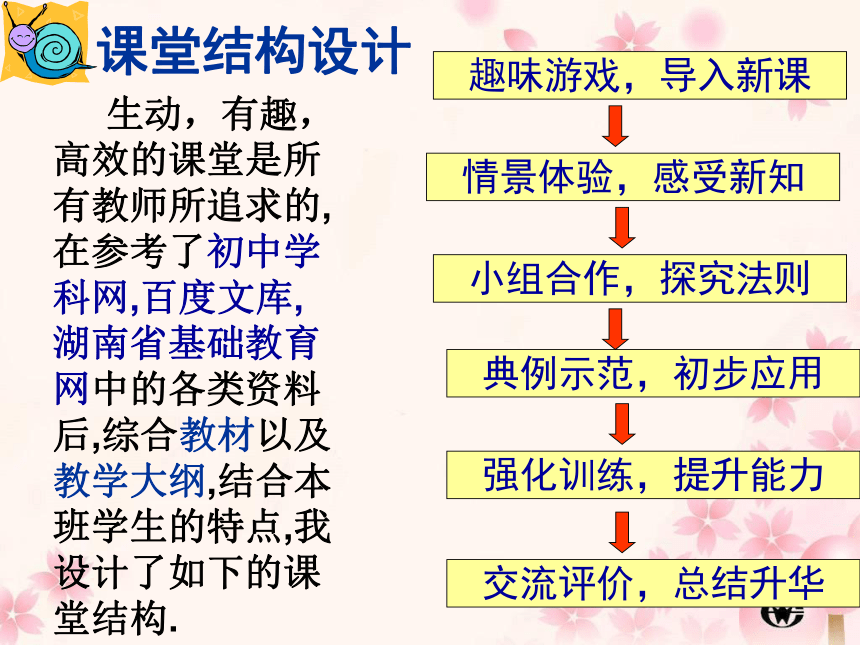
课堂结构设计
生动，有趣，高效的课堂是所有教师所追求的,
在参考了初中,百度文库,
湖南省基础教育网中的各类资料后,综合教材以及教学大纲,结合本班学生的特点,我设计了如下的课堂结构.
趣味游戏，导入新课
情景体验，感受新知
交流评价，总结升华
小组合作，探究法则
典例示范，初步应用
强化训练，提升能力
你还记得非负整数的乘法的意义是什么吗？
有理数可以做乘法运算吗？
如果可以，积又要怎么确定呢？
伸出你们的手，我们一般都有五根手指头。现在右手握拳，把你同桌弯曲的五根手指头，每次改变任意的两根手指的状态（弯曲的手指改变后变成伸直的，伸直的手指头改变后变成弯曲的，可以重复改变同一根），你能用“剪刀”把同桌的 “石头”变成“布”吗？
趣味游戏，导入新课
“石头” ＝
(－1)×(－1)×(－1)×(－1)×(－1)
“布” ＝
1×1×1×1×1
在一条由西向东的笔直马路上，取一个点O.以向东的路程为正数，则向西的路程为负数。小丽从点O出发，以5㎞/h的速度向西行走，那么经过了3h，她向西一共走了多远？
o
西
东
情景体验，感受新知
15
5
0
10
-5
-10
- 15
西
（－5）× 3
＝－（5 × 3）
分析：她向西一共走了（5×3）㎞.
又向西走为负
＝－15
3×（－5），
5×（－3），
（－5）×（－3）
应怎样计算？
小组合作，探究法则
你还记得小学学过的乘法对加法的分配律吗？
两个数的和与一个数相乘的积等于每个加数分别与这个数相乘再把所得的积加起来，这叫做乘法分配律
表达式是a (b + c) = a b + a c
计算： 3×5 ＋3×（－5）=？
互为相反数的两数相加为0.
所以：
3×（－5）＝
3×5＋3×（－5）
=3×[5＋（－5）]
=3×0
=0
－（ 3×5） ＝
－15
5×（－3） ＋5×3
=5×[（－3） ＋ 3]
=5×0 =0
（－5）×（－3） ＋ （－5） ×3
= （－5） ×[（－3） ＋ 3]
= （－5） ×0 =0
所以：
5×（－3）＝－（ 5×3） ＝－15
所以：
（－5） ×（－3）＝－[ （－5） ×3]
＝ －( －15)＝15
在上述4个式子中，我们从符号和绝对值两方面，找找看有什么规律？
（+5） （+3）=+15 （– 5） （+3） = –15
（– 5） （– 3）=+15 （+5） （– 3）= –15
同号两数相乘得 ，并把绝对值相乘；
异号两数相乘得 ，并把绝对值相乘；
正
负
例1 计算
（1）（－5）×（－4）；（2）2×（－3.5）
（3） ；（4）（－0. 57）×0
（2）2×（－3.5）
=－（2×3.5 ）
=－7
解： （1）（－5）×（－4）
=＋(5×4)
=20
（4）（－0. 57）×0
=0
（3）
=－
=－
求解中的第一步是
确定积的符号
第二步是
把绝对值相乘
0乘任何数都得 。
0
典例示范，初步应用
练一练：
(1) ( 2) ( 3) (2) ( 3) 9
(3) 6 （－9） (4) 0 ( 6)
(5) ( 6) 0 (6) 6 ( 1)
(7) ( 6) ( 1) (8) ( 6) 1
=6
=－27
=－54
=0
=0
=－6
=6
=－6
总结：
一个数乘以1都等于它 ；
一个数乘以-1都等于它的 .
本身
相反数
2.填表：
20
20
＋
8
2.5
－ 3
3
－
－10
0.3
＋
－1
－
－14
14
－
7
－2
积
绝对值的积
积的符号
因数
因数
强化训练，提升能力
1.“石头” ＝(－1)×(－1)×(－1)×(－1)×(－1)
“布” ＝(＋1)×(＋ 1)×(＋ 1)×(＋ 1)×(＋ 1)
计算中遇到小数与分数相乘、带分数与分数或小数相乘应怎么办？
2. 计算：
（1）－9×（－ ）
（2）（－7）×（－1）
（3）（ ）×（ ）
（4）（ ） ×（－0.5）
3.在足球比赛中，胜一场球，得分记为＋2, 负一场球，得分记为－2，某球队共负了五场球，最后得分应记为多少？
有理数乘法法则
3.任何数与 0 相乘，积仍为 0.
1.同号两数相乘得正，并把绝对值相乘；
2.异号两数相乘得负，并把绝对值相乘；
交流评价，总结升华
有理数乘法 有理数加法
同号
（－5）×（－3）= （－5）+（－3）=
异号
（－5）×3= （－5）+3=
任何数与0
作业：
P.35 A组 第1题
第2题（1）（2）题
能力提升 ①（－8）×[－(－ )]
② ×0.3
通过本节课的学习，夯实了学生的基础，题型从易到难，突现了从低级到高级的自然规律，满足了各种层次的学生学习的巩固和提高；题量适中，留给学生几分钟的自由思考和计算时间，提高了学生的探究能力与灵活运用能力。在游戏中，让学生体会到了数学知识在解决问题中的快捷性，增加了学生学习数学的热情。教学目标基本达到。