6.2.1 频率的稳定性(1) 课件(共24张PPT)
文档属性
| 名称 | 6.2.1 频率的稳定性(1) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 921.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 00:00:00 | ||
图片预览






文档简介
6.2.1频率的稳定性(1)
第六章 概率初步
2020-2021北师大版七年级数学下册
学习目标
1.通过试验让学生理解当试验次数较大时,实验的
频率具有稳定性,并据此能初步估计出某一事件
发生的可能性大小.
2.大量重复试验得到频率的稳定值的分析.(重点)
3.在活动中进一步发展学生合作交流的意识与能力,
发展学生的辩证思维能力.(难点)
小明和小丽在玩抛图钉游戏.
抛掷一枚图钉,落地后会
出现两种情况:钉尖朝上 ,
钉尖朝下.你认为钉尖朝上和
钉尖朝下的可能性一样
大吗?
导入新课
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的.
我的直觉跟你一样,但我不知道对不对.
不妨让我们用试验来验证吧!
导入新课
频率的稳定性
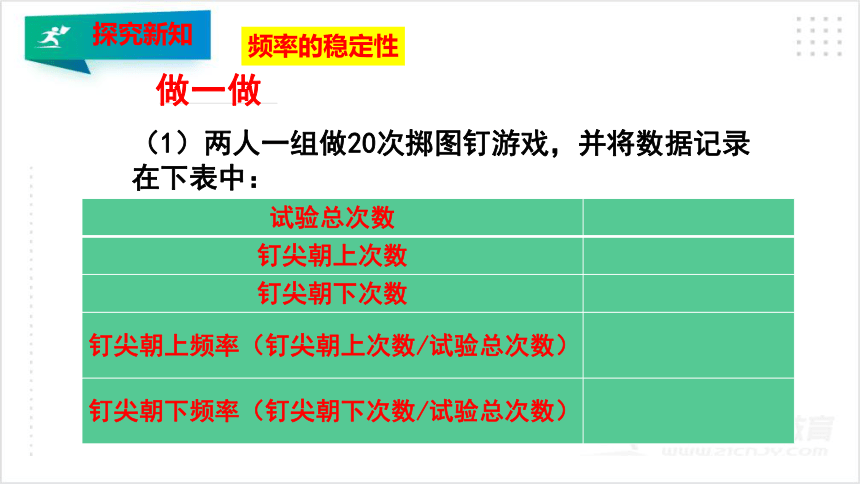
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
做一做
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
探究新知
频率:在n次重复试验中,事件A发生了m次,则
比值 称为事件A发生的频率.
(2)累计全班同学的实验2结果,并将试验数据
汇总填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数n
20
40
80
120
160
200
240
280
320
360
400
钉尖朝上次数m
钉尖朝上频率
探究新知
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
(3)根据上表完成下面的折线统计图:
探究新知
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
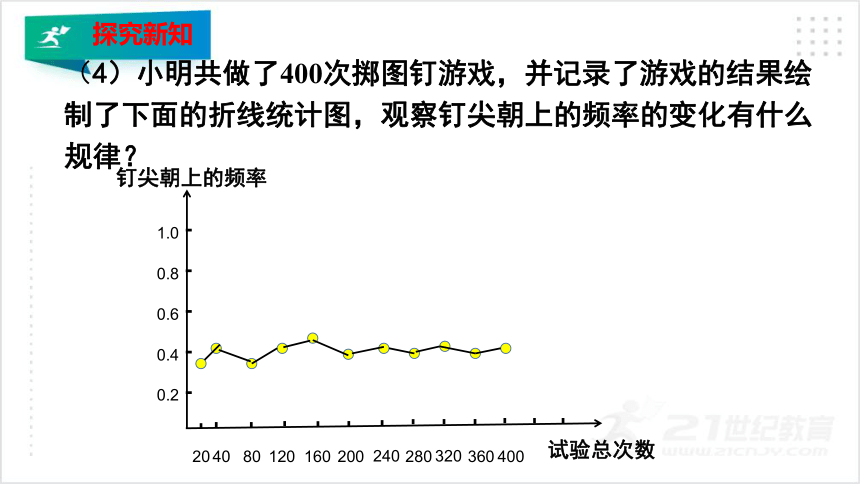
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察钉尖朝上的频率的变化有什么规律?
探究新知
在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
结论:
探究新知
议一议
(1)通过上面的试验,你认为钉尖朝上和钉尖
朝下的可能性一样大吗?你是怎样想的?
(2)小明和小丽一起做了1000次掷图钉的试验,
其中有640次钉尖朝上.据此,他们认为钉
尖朝上的可能性比钉尖朝下的可能性大.
你同意他们的说法吗?
探究新知
例1 在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有( )
A.5个 B.10个 C.15个 D.45个
C
例题讲解
例2 为了看图钉落地后钉尖着地的频率有多大,小明做了大量重复试验,发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着试验次数的增加,钉尖着地的频率稳定
在0.4附近
C.钉尖着地的概率约为0.4
D.前20次试验结束后,钉尖着地的次数一定是
8次
D
例题讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}射击总次数n
10
20
50
100
200
500
1000
击中靶心的次数m
9
16
41
88
168
429
861
击中靶心的频率m/n
(1)完成上表;
(2)根据上表画出该运动员击中靶心的频率的折线
统计图;
(3)观察画出的折线统计图,击中靶心的频率变化
有什么规律?
某射击运动员在同一条件下进行射击,结果如下表:
针对练习
1.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是 ( )
A.6 B.10 C.18 D.20
解析:根据题意得 =30%,解得n=20,所以这个不透明的盒子里大约有20个除颜色外其他完全相同的小球.故选D.
D
课堂练习
2.掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上
B.可能有5次正面向上
C.必有5次正面向上
D.不可能有10次正面向上
解析:因为一枚质地均匀的硬币只有正反两面,所以不管抛多少次,硬币正面朝上的可能性都是 ,所以掷一枚质地均匀的硬币10次,可能有5次正面向上.故选B.
B
课堂练习
3.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民
通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率
是31%和42%,则这个水塘里有鲤鱼 尾,
鲢鱼 尾.
310
270
课堂练习
4.养鱼专业户为了估计他承包的鱼塘里有多少条
鱼(假设这个塘里养的是同一种鱼),先捕上100
条做上标记,然后放回塘里,过了一段时间,
待带标记的鱼完全和塘里的鱼混合后,再捕上
100条,发现其中带标记的鱼有10条,鱼塘里大
约有鱼多少条?
解:设鱼塘里有鱼x条,根据题意可得
解得 x=1000.
答:鱼塘里有鱼1000条.
课堂练习
5.某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率,绘制折线图如下:
课堂练习
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
课堂练习
(3)若你是该厂的负责人,你将如何安排生产各种
颜色的产量?
红、黄、蓝、绿及其它颜色的生产比例大约为
4:2:1:2:1 .
(2)你能估计调查到10000名同学时,红色的频率
是多少吗?
估计调查到10000名同学时,红色的频率大约
仍是40%左右.
课堂练习
6. 任意掷一枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6),“6”朝上的概率是多少?
解:任意掷一枚均匀的小立方体,所有可能出现的结果 有6种:“1”朝上,“2”朝上,“3”朝上,“4”朝上,“5”朝上,“6”朝上,每种结果出现的概率都相等。其中, “6”朝上的结果只有1种,因此
P( “6”朝上)=
课堂练习
在试验次数很大时,钉尖朝上的频率都会在一个
常数附近摆动,即钉尖朝上的频率具有稳定性.
频率:在n次重复试验中,事件A发生了m次,则
比值 称为事件A发生的频率.
课堂小结
https://www.21cnjy.com/help/help_extract.php
第六章 概率初步
2020-2021北师大版七年级数学下册
学习目标
1.通过试验让学生理解当试验次数较大时,实验的
频率具有稳定性,并据此能初步估计出某一事件
发生的可能性大小.
2.大量重复试验得到频率的稳定值的分析.(重点)
3.在活动中进一步发展学生合作交流的意识与能力,
发展学生的辩证思维能力.(难点)
小明和小丽在玩抛图钉游戏.
抛掷一枚图钉,落地后会
出现两种情况:钉尖朝上 ,
钉尖朝下.你认为钉尖朝上和
钉尖朝下的可能性一样
大吗?
导入新课
直觉告诉我任意掷一枚图钉,钉尖朝上和钉尖朝下的可能性是不相同的.
我的直觉跟你一样,但我不知道对不对.
不妨让我们用试验来验证吧!
导入新课
频率的稳定性
(1)两人一组做20次掷图钉游戏,并将数据记录在下表中:
做一做
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数
钉尖朝上次数
钉尖朝下次数
钉尖朝上频率(钉尖朝上次数/试验总次数)
钉尖朝下频率(钉尖朝下次数/试验总次数)
探究新知
频率:在n次重复试验中,事件A发生了m次,则
比值 称为事件A发生的频率.
(2)累计全班同学的实验2结果,并将试验数据
汇总填入下表:
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}试验总次数n
20
40
80
120
160
200
240
280
320
360
400
钉尖朝上次数m
钉尖朝上频率
探究新知
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
(3)根据上表完成下面的折线统计图:
探究新知
20
40
80
120
200
240
160
320
280
0.2
400
360
1.0
0.6
0.8
0.4
钉尖朝上的频率
试验总次数
(4)小明共做了400次掷图钉游戏,并记录了游戏的结果绘制了下面的折线统计图,观察钉尖朝上的频率的变化有什么规律?
探究新知
在试验次数很大时,钉尖朝上的频率都会在一个常数附近摆动,即钉尖朝上的频率具有稳定性.
结论:
探究新知
议一议
(1)通过上面的试验,你认为钉尖朝上和钉尖
朝下的可能性一样大吗?你是怎样想的?
(2)小明和小丽一起做了1000次掷图钉的试验,
其中有640次钉尖朝上.据此,他们认为钉
尖朝上的可能性比钉尖朝下的可能性大.
你同意他们的说法吗?
探究新知
例1 在一个不透明的布袋中装有红色、白色玻璃球共60个,除颜色外其他完全相同.小明通过多次摸球试验后发现,其中摸到红色球的频率稳定在25%左右,则口袋中红色球可能有( )
A.5个 B.10个 C.15个 D.45个
C
例题讲解
例2 为了看图钉落地后钉尖着地的频率有多大,小明做了大量重复试验,发现钉尖着地的次数是实验总次数的40%,下列说法错误的是( )
A.钉尖着地的频率是0.4
B.随着试验次数的增加,钉尖着地的频率稳定
在0.4附近
C.钉尖着地的概率约为0.4
D.前20次试验结束后,钉尖着地的次数一定是
8次
D
例题讲解
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}射击总次数n
10
20
50
100
200
500
1000
击中靶心的次数m
9
16
41
88
168
429
861
击中靶心的频率m/n
(1)完成上表;
(2)根据上表画出该运动员击中靶心的频率的折线
统计图;
(3)观察画出的折线统计图,击中靶心的频率变化
有什么规律?
某射击运动员在同一条件下进行射击,结果如下表:
针对练习
1.一个不透明的盒子里有n个除颜色外其他完全相同的小球,其中有6个黄球.每次摸球前先将盒子里的球摇匀,任意摸出一个球记下颜色后再放回盒子,通过大量重复摸球试验后发现,摸到黄球的频率稳定在30%,那么可以推算出n大约是 ( )
A.6 B.10 C.18 D.20
解析:根据题意得 =30%,解得n=20,所以这个不透明的盒子里大约有20个除颜色外其他完全相同的小球.故选D.
D
课堂练习
2.掷一枚质地均匀的硬币10次,下列说法正确的是 ( )
A.每两次必有1次正面向上
B.可能有5次正面向上
C.必有5次正面向上
D.不可能有10次正面向上
解析:因为一枚质地均匀的硬币只有正反两面,所以不管抛多少次,硬币正面朝上的可能性都是 ,所以掷一枚质地均匀的硬币10次,可能有5次正面向上.故选B.
B
课堂练习
3.一水塘里有鲤鱼、鲫鱼、鲢鱼共1 000尾,一渔民
通过多次捕获实验后发现:鲤鱼、鲫鱼出现的频率
是31%和42%,则这个水塘里有鲤鱼 尾,
鲢鱼 尾.
310
270
课堂练习
4.养鱼专业户为了估计他承包的鱼塘里有多少条
鱼(假设这个塘里养的是同一种鱼),先捕上100
条做上标记,然后放回塘里,过了一段时间,
待带标记的鱼完全和塘里的鱼混合后,再捕上
100条,发现其中带标记的鱼有10条,鱼塘里大
约有鱼多少条?
解:设鱼塘里有鱼x条,根据题意可得
解得 x=1000.
答:鱼塘里有鱼1000条.
课堂练习
5.某厂打算生产一种中学生使用的笔袋,但无法确定各种颜色的产量,于是该文具厂就笔袋的颜色随机调查了5000名中学生,并在调查到1000名、2000名、3000名、4000名、5000名时分别计算了各种颜色的频率,绘制折线图如下:
课堂练习
(1)随着调查次数的增加,红色的频率如何变化?
随着调查次数的增加,红色的频率基本稳定在40%左右.
课堂练习
(3)若你是该厂的负责人,你将如何安排生产各种
颜色的产量?
红、黄、蓝、绿及其它颜色的生产比例大约为
4:2:1:2:1 .
(2)你能估计调查到10000名同学时,红色的频率
是多少吗?
估计调查到10000名同学时,红色的频率大约
仍是40%左右.
课堂练习
6. 任意掷一枚均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6),“6”朝上的概率是多少?
解:任意掷一枚均匀的小立方体,所有可能出现的结果 有6种:“1”朝上,“2”朝上,“3”朝上,“4”朝上,“5”朝上,“6”朝上,每种结果出现的概率都相等。其中, “6”朝上的结果只有1种,因此
P( “6”朝上)=
课堂练习
在试验次数很大时,钉尖朝上的频率都会在一个
常数附近摆动,即钉尖朝上的频率具有稳定性.
频率:在n次重复试验中,事件A发生了m次,则
比值 称为事件A发生的频率.
课堂小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
