6.2.2 平行四边形的判定 课件(共22张PPT)
文档属性
| 名称 | 6.2.2 平行四边形的判定 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 14:14:47 | ||
图片预览







文档简介
第2节 平行四边形的判定
(第2课时)
第六章 平行四边形
2021年春北师大版八年级数学下册
1 探索并证明“对角线互相平分的四边形是平行四边形”;(重点)
2 应用平行四边形的判定定理解决问题.(难点)
学习目标
前面我们已经知道:
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
你还能找到其他的判定方法吗?
新课导入
由对角线的关系判定平行四边形
你同意他的想法吗?你能证明他的猜想吗?请你试一试.
如图,将两根木条AC,BD的中点重叠,并用钉子固定,四边形ABCD看起来是平行四边形. 于是我猜想:对角线互相平分的四边形是平行四边形.
猜想:对角线互相平分的四边形是平行四边形.
探究新知
例1 已知:如图,四边形ABCD的两条对角线AC与BD相交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
例题讲解
证明:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△AOD≌ △COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).
符号语言:
∴四边形ABCD是平行四边形
定理:对角线互相平分的四边形是平行四边形。
∵OA=OC,0B=0D
B
D
A
C
O
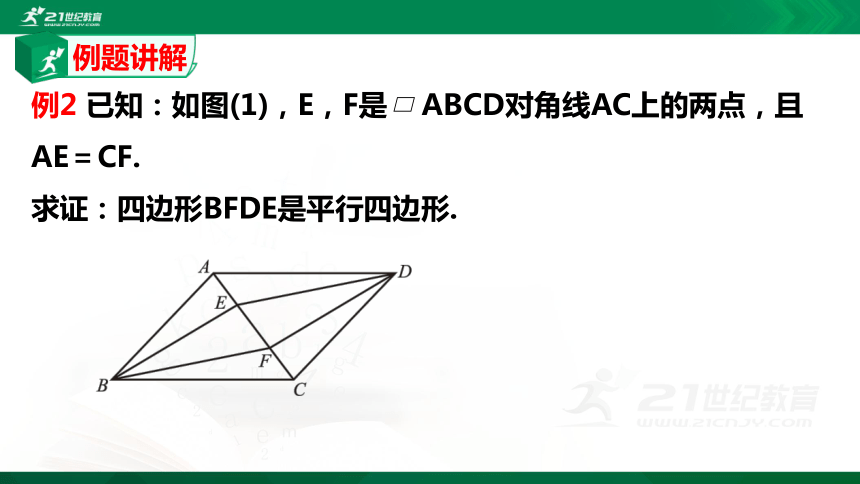
例2 已知:如图(1),E,F是 ABCD对角线AC上的两点,且AE=CF.
求证:四边形BFDE是平行四边形.
例题讲解
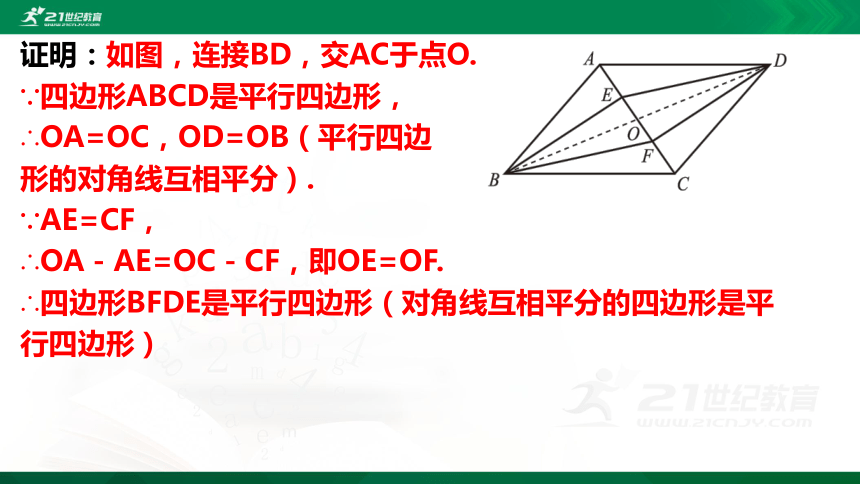
证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB(平行四边
形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
例3 已知:如图,在四边形ABCD中∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
例题讲解
证明:∵∠A =∠C,∠B =∠D,∠A+∠C+∠B+∠D=360°,
∴∠A+∠B=180°.
∴AD∥CB,
同理可得:AB∥CD.
∴四边形ABCD是平行四边形(平行四边形的定义).
两组对角分别相等的四边形是平行四边形.
平行四边形判定方法的综合应用
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
探究新知
例4 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;其中正确的说法是( )
A.①② B.①③ C.②③ D.②③
C
例题讲解
1 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
课堂练习
2.下列给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判断四边形ABCD是平行四边形的是( )
A.1∶2∶3∶4 B.2∶2∶3∶3
C.2∶3∶2∶3 D.2∶3∶3∶2
3 如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
4 如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
A.6 B.12
C.20 D.24
5 如图,在?ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或② B.②或③
C.③或④ D.①或③
5 如图,在□ ABCD中,对角线AC与BD相交于点O,点E,F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
从边来判定
1 两组对边分别平行的四边形是平行四边形
2 两组对边分别相等的四边形是平行四边形
3 一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
课堂小结
谢谢聆听
(第2课时)
第六章 平行四边形
2021年春北师大版八年级数学下册
1 探索并证明“对角线互相平分的四边形是平行四边形”;(重点)
2 应用平行四边形的判定定理解决问题.(难点)
学习目标
前面我们已经知道:
两组对边分别相等的四边形是平行四边形.
一组对边平行且相等的四边形是平行四边形.
你还能找到其他的判定方法吗?
新课导入
由对角线的关系判定平行四边形
你同意他的想法吗?你能证明他的猜想吗?请你试一试.
如图,将两根木条AC,BD的中点重叠,并用钉子固定,四边形ABCD看起来是平行四边形. 于是我猜想:对角线互相平分的四边形是平行四边形.
猜想:对角线互相平分的四边形是平行四边形.
探究新知
例1 已知:如图,四边形ABCD的两条对角线AC与BD相交于点O,并且OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
例题讲解
证明:∵OA=OC,OD=OB,∠AOD=∠COB,
∴△AOD≌ △COB.
∴AD=CB,∠ADO=∠CBO.
∴AD∥CB.
∴四边形ABCD是平行四边形(一组对边平行且相等的四边形是平行四边形).
符号语言:
∴四边形ABCD是平行四边形
定理:对角线互相平分的四边形是平行四边形。
∵OA=OC,0B=0D
B
D
A
C
O
例2 已知:如图(1),E,F是 ABCD对角线AC上的两点,且AE=CF.
求证:四边形BFDE是平行四边形.
例题讲解
证明:如图,连接BD,交AC于点O.
∵四边形ABCD是平行四边形,
∴OA=OC,OD=OB(平行四边
形的对角线互相平分).
∵AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BFDE是平行四边形(对角线互相平分的四边形是平行四边形)
例3 已知:如图,在四边形ABCD中∠A=∠C,∠B=∠D.
求证:四边形ABCD是平行四边形.
例题讲解
证明:∵∠A =∠C,∠B =∠D,∠A+∠C+∠B+∠D=360°,
∴∠A+∠B=180°.
∴AD∥CB,
同理可得:AB∥CD.
∴四边形ABCD是平行四边形(平行四边形的定义).
两组对角分别相等的四边形是平行四边形.
平行四边形判定方法的综合应用
平行四边形的判定方法:
(1)定义:两组对边分别平行的四边形是平行四边形.
(2)两组对边分别相等的四边形是平行四边形.
(3)一组对边平行且相等的四边形是平行四边形.
(4)两组对角分别相等的四边形是平行四边形.
(5)对角线互相平分的四边形是平行四边形.
探究新知
例4 在四边形ABCD中,AC交BD于点O,且AB∥CD,给出以下四种说法:
①如果再加上条件“BC=AD”,那么四边形ABCD一定是平行四边形;②如果再加上条件“∠BAD=∠BCD”,那么四边形ABCD一定是平行四边形;③如果再加上条件“AO=OC”,那么四边形ABCD一定是平行四边形;其中正确的说法是( )
A.①② B.①③ C.②③ D.②③
C
例题讲解
1 下列说法错误的是( )
A.对角线互相平分的四边形是平行四边形
B.两组对边分别相等的四边形是平行四边形
C.一组对边平行且相等的四边形是平行四边形
D.一组对边相等,另一组对边平行的四边形是平行四边形
课堂练习
2.下列给出了四边形ABCD中∠A、∠B、∠C、∠D的度数之比,其中能判断四边形ABCD是平行四边形的是( )
A.1∶2∶3∶4 B.2∶2∶3∶3
C.2∶3∶2∶3 D.2∶3∶3∶2
3 如图,在四边形ABCD中,对角线AC,BD相交于点O,下列条件不能判定四边形ABCD为平行四边形的是( )
A.AB∥CD,AD∥BC
B.OA=OC,OB=OD
C.AD=BC,AB∥CD
D.AB=CD,AD=BC
4 如图,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为( )
A.6 B.12
C.20 D.24
5 如图,在?ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或② B.②或③
C.③或④ D.①或③
5 如图,在□ ABCD中,对角线AC与BD相交于点O,点E,F分别是OA和OC的中点,四边形BFDE是平行四边形吗?请说明理由.
从边来判定
1 两组对边分别平行的四边形是平行四边形
2 两组对边分别相等的四边形是平行四边形
3 一组对边平行且相等的四边形是平行四边形
从角来判定
两组对角分别相等的四边形是平行四边形
从对角线来判定
两条对角线互相平分的四边形是平行四边形
平行四边形的判定方法
课堂小结
谢谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
