6.2.1 平行四边形的判定 课件(共21张PPT)
文档属性
| 名称 | 6.2.1 平行四边形的判定 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 00:00:00 | ||
图片预览





文档简介
第2节
平行四边形的判定
(第1课时)
第六章
平行四边形
2021年春北师大版八年级数学下册
1
探索平行四边形的判别条件;(重点)
2
掌握应用判别方法对一些平行四边形的判别进行说理。(难点)
学习目标
平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分;
我们已经学行四边形的这些性质,那么它们的逆命题各是什么呢?
新课导入
平行四边形对角线互相平分
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
思考:我们得到的这些逆命题都成立吗?我们一起探讨一下吧!
探究新知
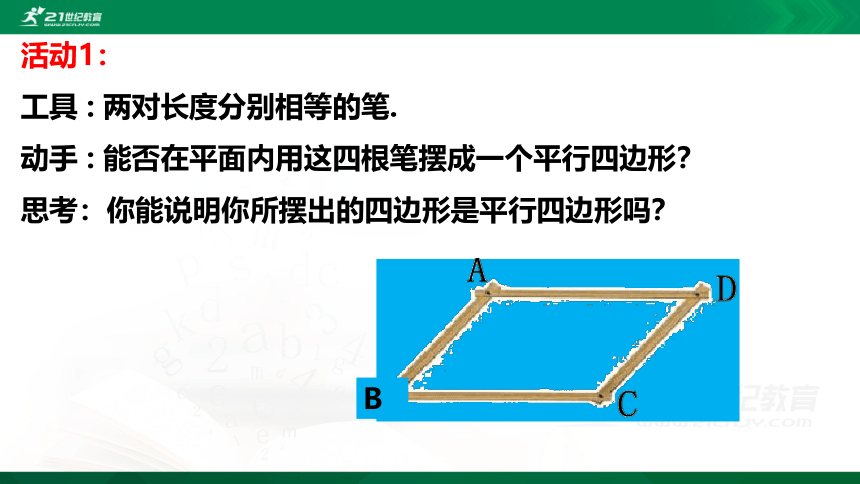
活动1:
工具
:
两对长度分别相等的笔.
动手
:
能否在平面内用这四根笔摆成一个平行四边形?
思考:你能说明你所摆出的四边形是平行四边形吗?
B
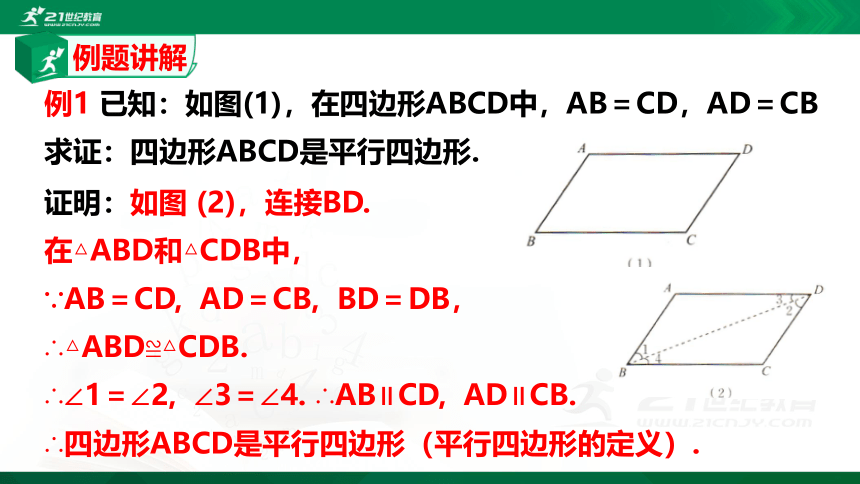
例1
已知:如图(1),在四边形ABCD中,AB=CD,AD=CB
求证:四边形ABCD是平行四边形.
证明:如图
(2),连接BD.
在△ABD和△CDB中,
∵AB=CD,
AD=CB,
BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,
∠3=∠4.
∴AB∥CD,
AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
例题讲解
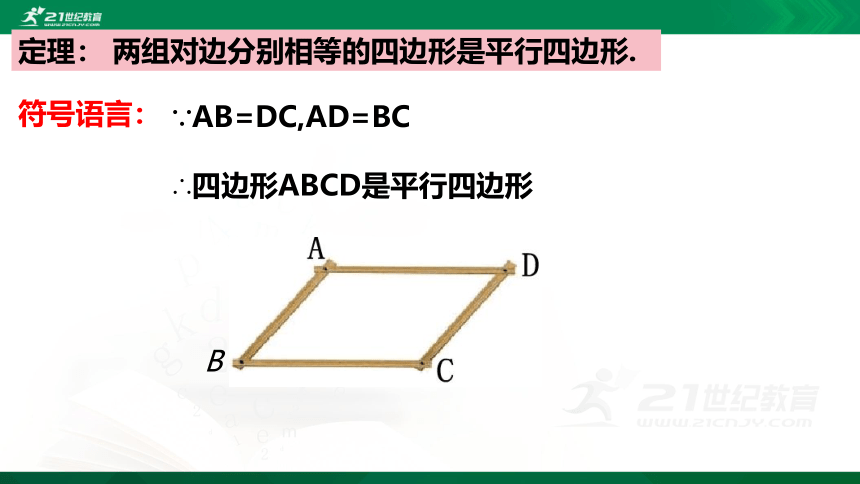
定理:
两组对边分别相等的四边形是平行四边形.
B
符号语言:
∵AB=DC,AD=BC
∴四边形ABCD是平行四边形
由一组对边的关系判定平行四边形
活动2
工具:
两根长度相等的笔,两条平行线(可利用横格线).
动手:
1
请利用两根长度相等的笔能摆出以笔顶端为顶点的平行四边形吗?
探究新知
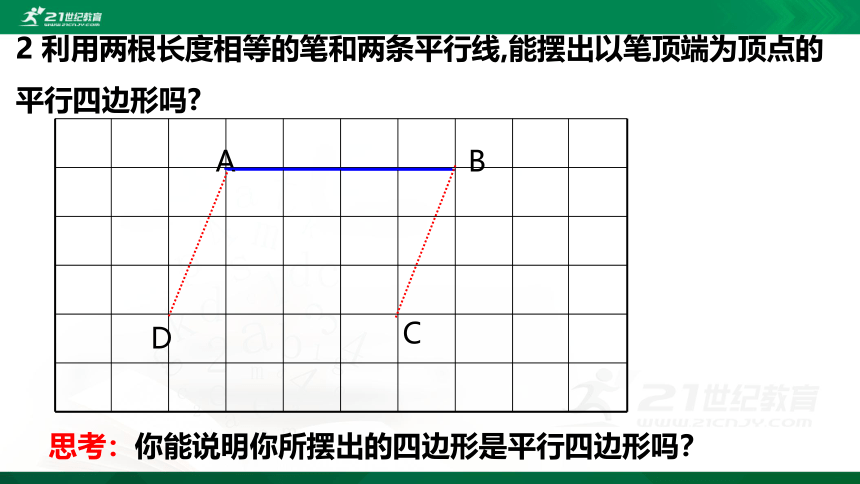
2
利用两根长度相等的笔和两条平行线,能摆出以笔顶端为顶点的平行四边形吗?
A
B
C
D
思考:你能说明你所摆出的四边形是平行四边形吗?
证明:如图
(2),连接AC.
∵AB∥CD,∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相
等的四边形是平行
四边形).
例2
已知:如图(1),在四边形ABCD中,AB
CD.
求证:四边形ABCD是平行四边形.
例题讲解
定理:一组对边平行且相等的四边形是平行四边形.
B
符号语言:
∵AB
DC
∴四边形ABCD是平行四边形
∥
=
例3
已知:如图,在
ABCD中,E,
F分别为AD和CB的中点.
证明:求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),AD∥CB(平行四边形的定义)
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形(一组对边平行且相等的四边形是平行四边形).
例题讲解
1
下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形
课堂练习
2
下列条件不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
3
在四边形ABCD中,AD=BC,若四边形ABCD是平行四边形,则还应满足( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
4
小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③
5
如图,在?ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或②
B.②或③
C.③或④
D.①或③
6
□
ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?
有边判定四边形是平行四边形的方法有:
1
定义:两组对边分别平行的四边形是平行四边形.
2
两组对边分别相等的四边形是平行四边形.
3
一组对边平行且相等的四边形是平行四边形.
课堂小结
谢谢聆听
平行四边形的判定
(第1课时)
第六章
平行四边形
2021年春北师大版八年级数学下册
1
探索平行四边形的判别条件;(重点)
2
掌握应用判别方法对一些平行四边形的判别进行说理。(难点)
学习目标
平行四边形的性质
平行四边形对边平行;
平行四边形对边相等;
平行四边形对角相等;
平行四边形对角线互相平分;
我们已经学行四边形的这些性质,那么它们的逆命题各是什么呢?
新课导入
平行四边形对角线互相平分
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
两组对边分别相等的四边形是平行四边形;
思考:我们得到的这些逆命题都成立吗?我们一起探讨一下吧!
探究新知
活动1:
工具
:
两对长度分别相等的笔.
动手
:
能否在平面内用这四根笔摆成一个平行四边形?
思考:你能说明你所摆出的四边形是平行四边形吗?
B
例1
已知:如图(1),在四边形ABCD中,AB=CD,AD=CB
求证:四边形ABCD是平行四边形.
证明:如图
(2),连接BD.
在△ABD和△CDB中,
∵AB=CD,
AD=CB,
BD=DB,
∴△ABD≌△CDB.
∴∠1=∠2,
∠3=∠4.
∴AB∥CD,
AD∥CB.
∴四边形ABCD是平行四边形(平行四边形的定义).
例题讲解
定理:
两组对边分别相等的四边形是平行四边形.
B
符号语言:
∵AB=DC,AD=BC
∴四边形ABCD是平行四边形
由一组对边的关系判定平行四边形
活动2
工具:
两根长度相等的笔,两条平行线(可利用横格线).
动手:
1
请利用两根长度相等的笔能摆出以笔顶端为顶点的平行四边形吗?
探究新知
2
利用两根长度相等的笔和两条平行线,能摆出以笔顶端为顶点的平行四边形吗?
A
B
C
D
思考:你能说明你所摆出的四边形是平行四边形吗?
证明:如图
(2),连接AC.
∵AB∥CD,∴∠BAC=∠DCA.
又∵AB=CD,AC=CA,
∴△ABC≌△CDA.
∴BC=DA.
∴四边形ABCD是平行四边形(两组对边分别相
等的四边形是平行
四边形).
例2
已知:如图(1),在四边形ABCD中,AB
CD.
求证:四边形ABCD是平行四边形.
例题讲解
定理:一组对边平行且相等的四边形是平行四边形.
B
符号语言:
∵AB
DC
∴四边形ABCD是平行四边形
∥
=
例3
已知:如图,在
ABCD中,E,
F分别为AD和CB的中点.
证明:求证:四边形BFDE是平行四边形.
∵四边形ABCD是平行四边形,
∴AD=CB(平行四边形的对边相等),AD∥CB(平行四边形的定义)
∵E,F分别是AD和CB的中点,
∴ED=FB,ED∥FB.
∴四边形DFDE是平行四边形(一组对边平行且相等的四边形是平行四边形).
例题讲解
1
下列图形中,一定可以拼成平行四边形的是( )
A.两个等腰三角形
B.两个直角三角形
C.两个锐角三角形
D.两个全等三角形
课堂练习
2
下列条件不能判定四边形ABCD是平行四边形的是( )
A.∠A=∠C,∠B=∠D
B.∠A=∠B=∠C=90°
C.∠A+∠B=180°,∠B+∠C=180°
D.∠A+∠B=180°,∠C+∠D=180°
3
在四边形ABCD中,AD=BC,若四边形ABCD是平行四边形,则还应满足( )
A.∠A+∠C=180°
B.∠B+∠D=180°
C.∠A+∠B=180°
D.∠A+∠D=180°
4
小敏不慎将一块平行四边形玻璃打碎成如图所示的四块,为了能在商店配到一块与原来相同的平行四边形玻璃,她带了两块碎玻璃,其编号应该是( )
A.①②
B.①④
C.③④
D.②③
5
如图,在?ABCD中,点E,F分别在AD,BC上,若要使四边形AFCE是平行四边形,可以添加的条件是( )
①AF=CF;②AE=CE;③BF=DE;④AF∥CE.
A.①或②
B.②或③
C.③或④
D.①或③
6
□
ABCD的对角线相交于点O,点E、F、G、H分别是OA、OB、OC、OD的中点。四边形EFGH是平行四边形吗?为什么?
有边判定四边形是平行四边形的方法有:
1
定义:两组对边分别平行的四边形是平行四边形.
2
两组对边分别相等的四边形是平行四边形.
3
一组对边平行且相等的四边形是平行四边形.
课堂小结
谢谢聆听
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
