第9章整式乘法与因式分解 单元测试-2020~2021年苏科版数学七年级下册(Word版 含解析)
文档属性
| 名称 | 第9章整式乘法与因式分解 单元测试-2020~2021年苏科版数学七年级下册(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 11:50:43 | ||
图片预览




文档简介
1073150010287000
第9章整式乘法与因式分解章节复习限时作业
一、选择题(本大题共8小题,共24.0分)
下列运算正确的是(????)
A. a2?a5=a10 B. (3a3)2=6a6
C. (a+b)2=a2+b2 D. (a+2)(a?3)=a2?a?6
计算(a?2)(a+3)的结果是(????)
A. a2?6 B. a2+a?6 C. a2+6 D. a2?a+6
下列各式由左到右的变形中,属于分解因式的是(????)
A. a(m+n)=am+an
B. a2?b2?c2=(a?b)(a+b)?c2
C. 10x2?5x=5x(2x?1)
D. x2?16+6x=(x+4)(x?4)+6x
若x+m与2?x的乘积中不含x的一次项,则实数m的值为(????)
A. ?2 B. 2 C. 0 D. 1
下列运算正确的是(????)
A. (?2a)2=?4a2 B. (a+b)2=a2+b2
C. (a5)2=a7 D. (?a+2)(?a?2)=a2?4
下列各式能用平方差公式计算的是(????)
A. (2a+b)(2b?a) B. (x+1)(?x?1)
C. (?m?n)(?m+n) D. (3x?y)(?3x+y)
若多项式a2+ka+9是完全平方式,则常数k的值为(????)
A. 6 B. 3 C. ±6 D. ±3
下面因式分解错误的是(????)
A. x2?y2=(x+y)(x?y) B. x2?8x+16=(x?4)2
C. 2x2?2xy=2x(x?y) D. x2+y2=(x+y)2
二、填空题(本大题共8小题,共24.0分)
已知a?2b=?2,则代数式a(b?2)?b(a?4)的值为______.
因式分解:3x3?12x=______.
若关于x的二次三项式x2+ax+14是完全平方式,则a的值是______.
已知:m?n=6,mn=1,则m2+n2=______.
若a?2b=3,则2a?4b?5=_________.
若?xa+by5与3x4y2b?a的和是单项式,则(2a+2b)(a?3b)的值为??????????.
已知a+b=10,a?b=8,则a2?b2=______.
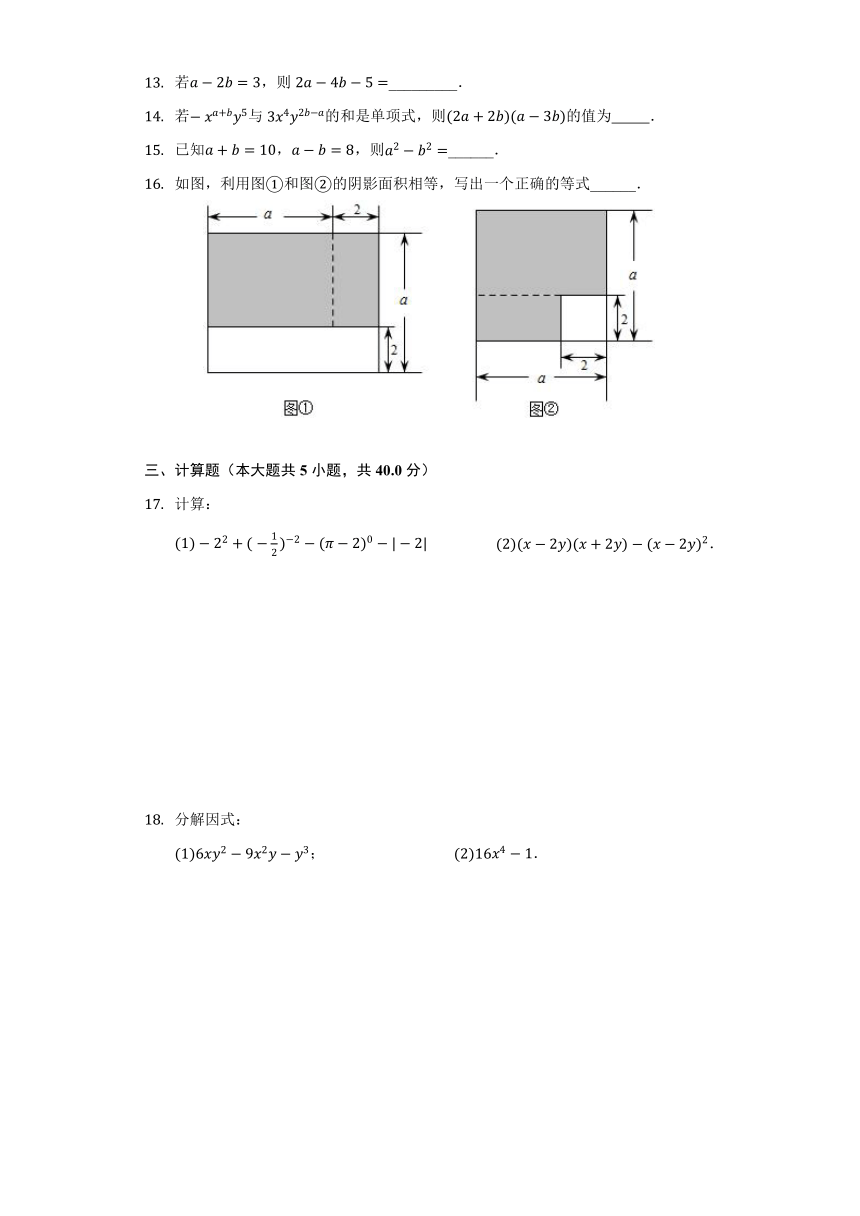
如图,利用图①和图②的阴影面积相等,写出一个正确的等式______.
center0
三、计算题(本大题共5小题,共40.0分)
计算:
(1)?22+(?12)?2?(π?2)0?|?2| (2)(x?2y)(x+2y)?(x?2y)2.
分解因式:
(1)6xy2?9x2y?y3; (2)16x4?1.
先化简,再求值:(a+3)2?(a+1)(a?1)?2(2a+4),其中a=?12.
已知?(a+b)2=7,(a?b)2=3,求:
(1)ab的值.?????????
(2)a2+b2的值.
发现与探索.
(1)根据小明的解答将下列各式因式分解
小明的解答:a2?6a+5=a2?6a+9?9+5=(a?3)2?4=(a?5)(a?1)
①a2?12a+20
②(a?1)2?8(a?1)+7
③a2?6ab+5b2
(2)根据小丽的思考解决下列问题:
小丽的思考:代数式(a?3)2+4无论a取何值(a?3)2都大于等于0,再加上4,则代数式(a?3)2+4大于等于4,则(a?3)2+4有最小值为4.
①说明:代数式a2?12a+20的最小值为?16.
②请仿照小丽的思考解释代数式?(a+1)2+8的最大值为8,并求代数式?a2+12a?8的最大值.
四、解答题(本大题共4小题,共32.0分)
对于任意有理数a、b、c、d,我们规定符号(a,b)?(c,d)=ad?bc,
例如:(1,3)?(2,4)=1×4?2×3=?2.
(1)求(?2,3)?(4,5)的值为______;
(2)求(3a+1,a?2)?(a+2,a?3)的值,其中a2?4a+1=0.
甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2?7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x?3.
(1)求a,b的值;
(2)请计算这道题的正确结果.
阅读理解题:
定义:如果一个数的平方等于?1,记为i2=?1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2?i)+(5+3i)=(2+5)+(?1+3)i=7+2i;
(1+i)×(2?i)=1×2?i+2×i?i2=2+(?1+2)i+1=3+i;
根据以上信息,完成下列问题:
(1)填空:i3=______,i4=______;
(2)计算:(1+i)×(3?4i);
(3)计算:i+i2+i3+…+i2017.
动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:______,______;
(2)请写出三个代数式(a+b)2,(a?b)2,ab之间的一个等量关系:______;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=6,xy=5,求x?y的值.
center0
答案和解析
1.【答案】D
【解析】解:A、原式=a7,不符合题意;
B、原式=9a6,不符合题意;
C、原式=a2+2ab+b2,不符合题意;
D、原式=a2?a?6,符合题意,
故选:D.
各式计算得到结果,即可作出判断.
此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
2.【答案】B
【解析】
【分析】
此题考查多项式的乘法,关键是根据多项式乘法的法则解答.
根据多项式的乘法解答即可.
【解答】
解:(a?2)(a+3)=a2+3a?2a?6=a2+a?6,
故选:B.
3.【答案】C
【解析】
【分析】
本题考查因式分解的概念,解题的关键是正确理解因式分解的概念,属于基础题.
根据因式分解的定义即可判断.
【解答】
解:A.该变形为去括号,故A不是因式分解;
B.该等式右边没有化为几个整式的乘积形式,故B不是因式分解;
C.符合因式分解定义,故C是因式分解;
D该等式右边没有化为几个整式的乘积形式,故D不是因式分解.
故选:C.
4.【答案】B
【解析】
【分析】
此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
根据多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,计算即可.
【解答】
解:根据题意得:
(x+m)(2?x)=2x?x2+2m?mx=?x2+(2?m)x+2m,
∵x+m与2?x的乘积中不含x的一次项,
∴m=2;
故选:B.
5.【答案】D
【解析】
【分析】
此题考查整式的运算,掌握各运算法则是关键,还要注意符号的处理.
按照积的乘方运算、完全平方公式、幂的乘方、平方差公式分别计算,再选择.
【解答】
解:A.(?2a)2=4a2,故选项A不符合题意;
B.(a+b)2=a2+2ab+b2,故选项B不符合题意;
C.(a5)2=a10,故选项C不符合题意;
D.(?a+2)(?a?2)=a2?4,故选项D符合题意.
故选:D.
6.【答案】C
【解析】解:A、B、D都不是平方差公式;
C、(?m?n)(?m+n)=(?m)2?n2,故C正确;
故选:C.
根据两数和乘以这两个数的差等于这两个数的平方差,可得答案.
本题考查了平方差公式,利用了平方差公式.
7.【答案】C
【解析】解:∵a2+ka+9=a2+ka+32,
∴ka=±2×a×3,
解得k=±6.
故选为:C.
先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定k的值.
本题主要考查了完全平方式,根据平方项确定出这两个数是解题的关键,也是难点,熟记完全平方公式对解题非常重要.
8.【答案】D
【解析】解:A、x2?y2=(x+y)(x?y),正确,不合题意;
B、x2?8x+16=(x?4)2,正确,不合题意;
C、2x2?2xy=2x(x?y),正确,不合题意;
D、x2+y2≠(x+y)2,此选项错误,符合题意.
故选:D.
分别利用完全平方公式以及平方差公式分解因式,进而判断得出答案.
此题主要考查了公式法以及提取公因式法分解因式,熟练应用乘法公式是解题关键.
9.【答案】4
【解析】解:a(b?2)?b(a?4)
=ab?2a?ab+4b
=?2a+4b
=?2(a?2b),
∵a?2b=?2,
∴原式=?2×(?2)=4.
故答案为:4.
直接利用单项式乘多项式计算,再把已知代入得出答案.
此题主要考查了单项式乘多项式,正确将原式变形是解题关键.
10.【答案】3x(x+2)(x?2)
【解析】解:3x3?12x
=3x(x2?4)
=3x(x+2)(x?2)
故答案是:3x(x+2)(x?2).
首先提公因式3x,然后利用平方差公式即可分解.
本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.
11.【答案】±1
【解析】解:中间一项为加上或减去x的系数和12积的2倍,
故a=±1,
解得a=±1,
故答案为:±1.
这里首末两项是x和12这两个数的平方,那么中间一项为加上或减去x的系数和12积的2倍,故?a=±1,求解即可
本题考查了完全平方式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.关键是注意积的2倍的符号,避免漏解.
12.【答案】38
【解析】解:∵(m?n)2=m2+n2?2mn,
∵36=m2+n2?2,
∴m2+n2=38,
故答案为38.
根据完全平方公式(m?n)2=m2+n2?2mn即可解题.
本题考查了完全平方公式的运用,解题的关键是正确运用(m?n)2=m2+n2?2mn.
13.【答案】1
【解析】
【分析】
此题考查整式的化简求值,根据题意,将原式变形为2(a?2b)?5,然后用整体代入法求解即可.
【解答】
解:∵a?2b=3
∴原式=2a?2b?5=2×3?5=1
故答案为1?.
14.【答案】?64
【解析】
【分析】
此题考查了多项式乘多项式,以及合并同类项,熟练掌握同类项性质及运算法则是解本题的关键.根据题意得到两式为同类项,确定出a与b的值,代入原式计算即可求出值.
【解答】
解:∵?xa+by5与3x4y2b?a的和是单项式,
∴?xa+by5与3x4y2b?a为同类项,即
a+b=4?①
2b?a=5?②
①+②得b=3,再代入①得a=1,
则(2a+2b)(a?3b)=(2+6)×(1?9)=?64,
故答案为:?64
15.【答案】80
【解析】
【分析】
本题考查平方差公式,解题的关键是熟练运用平方差公式,本题属于基础题型.根据平方差公式即可求出答案.
【解答】
解:∵(a+b)(a?b)=a2?b2,a+b=10,a?b=8,
∴a2?b2=10×8=80.
故答案为80.
16.【答案】(a+2)(a?2)=a2?4
【解析】解:①阴影部分的面积=(a+2)(a?2);
②阴影部分的面积=a2?22=a2?4;
∴(a+2)(a?2)=a2?4,
故答案为(a+2)(a?2)=a2?4;
①阴影部分的面积=(a+2)(a?2);
②阴影部分的面积=a2?22=a2?4;即可求解.
本题考查平方差公式的几何背景;理解题意,结合图形面积的关系得到公式,并能灵活运用公式是解题的关键.
17.【答案】解:(1)原式=?4+4?1?2=?3;
(2)原式=x2?4y2?x2+4xy?4y2=4xy?8y2.
【解析】(1)原式利用零指数幂、负整数指数幂法则和绝对值的代数意义化简,计算即可得到结果;
(2)原式利用平方差公式以及完全平方公式化简,去括号合并即可得到结果.
本题考查了平方差公式以及完全平方公式,熟练掌握公式是解本题的关键.
18.【答案】解:(1)原式=?y(y2?6xy+9x2)
=?y(y?3x)2;
(2)原式=(4x2+1)(4x2?1)
=(4x2+1)(2x+1)(2x?1).
【解析】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
(1)原式提取公因式,再利用完全平方公式分解即可;
(2)原式利用平方差公式分解即可.
19.【答案】解:
原式=a2+6a+9?(a2?1)?4a?8
=2a+2
将a=?12代入原式=2×(?12)+2=1
【解析】注意到(a+3)2可以利用完全平方公式进行展开,(a+1)(a?1)利润平方差公式可化为(a2?1),则将各项合并即可化简,最后代入a=?12进行计算.
本题主要考查整式的混合运算,灵活运用两条乘法公式:完全平方公式和平方差公式是解题的关键,同时,在去括号的过程中要注意括号前的符号,若为负号,去括号后,括号里面的符号要改变
20.【答案】解:(1)∵(a+b)2=a2+2ab+b2=7①,(a?b)2=a2?2ab+b2=3②,
∴①?②得:4ab=4,即ab=1;
(2)①+②得:2(a2+b2)=10,即a2+b2=5.
【解析】利用完全平方公式将已知等式左边展开,分别记作①和②,
(1)①?②后,即可求出ab的值;(2)①+②,整理即可求出a2+b2的值.
此题考查了完全平方公式的运用,熟练掌握完全平方公式是解本题的关键.
21.【答案】解:(1)①a2?12a+20
=a2?12a+36?36+20
=(a?6)2?42
=(a?10)(a?2);
②(a?1)2?8(a?1)+12
=(a?1)2?8(a?1)+16?16+12
=(a?5)2?22
=(a?7)(a?3);
③a2?6ab+5b2
=a2?6ab+9b2?9b2+5b2
=(a?3b)2?4b2
=(a?5b)(a?b);
(2)①a2?12a+20
=a2?12a+36?36+20
=(a?6)2?16,
无论a取何值(a?6)2都大于等于0,再加上?16,
则代数式(a?6)2?16大于等于?16,
则a2?12a+20的最小值为?16;
②无论a取何值?(a+1)2都小于等于0,再加上8,
则代数式?(a+1)2+8小于等于8,
则?(a+1)2+8的最大值为8,
?a2+12a?8.
=?(a2?12a+8)
=?(a2?12a+36?36+8)
=?(a?6)2+36?8
=?(a?6)2+28
无论a取何值?(a?6)2都小于等于0,再加上28,
则代数式?(a?6)2+28小于等于28,
则?a2+12a?8的最大值为28.
【解析】本题考查的是因式分解的应用、偶次方的非负性,掌握完全平方公式、平方差公式、偶次方的非负性是解题的关键.
(1)仿照小明的解答过程、利用完全平方公式、平方差公式计算;
(2)仿照小丽的思考过程,利用完全平方公式、平方差公式计算、偶次方的非负性解答.
22.【答案】(1)?22;
(2)(3a+1,a?2)?(a+2,a?3)
=(3a+1)(a?3)?(a?2)(a+2)
=3a2?9a+a?3?(a2?4)
=3a2?9a+a?3?a2+4
=2a2?8a+1,
∵a2?4a+1=0,
∴a2=4a?1,
∴3a+1,a?2)?(a+2,a?3)=2(4a?1)?8a+1=?1.
【解析】解:(1)(?2,3)?(4,5)=?2×5?3×4=?10?12=?22;
故答案为:?22;
(2)见答案.
(1)利用新定义得到(?2,3)?(4,5)=?2×5?3×4,然后进行有理数的混合运算即可;
(2)利用新定义得到原式=(3a+1)(a?3)?(a?2)(a+2),然后去括号后合并,最后利用整体代入的方法计算.
本题考查了整式的混合运算?化简求值:先按运算顺序把整式化简,再把对应字母的值代入求整式的值.有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
23.【答案】解:(1)由题意,得(x?a)(2x+b)=2x2?7x+3,
2x2+(b?2a)x?ab=2x2?7x+3,
得b?2a=?7,
(x+a)(x+b)=x2+2x?3,
x2+(a+b)x+ab=x2+2x?3,
得a+b=2,
由b?2a=?7a+b=2,
得a=3b=?1,
(2)把a=3b=?1代入整式(x+a)(2x+b),得
(x+3)(2x?1)
=2x2?x+6x?3,
=2x2+5x?3.
【解析】此题考查了多项式乘多项式,解题的关键是根据多项式乘多项式的运算法则分别进行计算,是常考题型,解题时要细心.
(1)先按甲、乙错误的说法得出关于a、b的二元一次方程组,求出a,b的值;
(2)把a,b的值代入原式求出整式乘法的正确结果.
24.【答案】解:(1)?i;1;
(2)(1+i)×(3?4i)
=3?4i+3i?4i2
=3?i+4
=7?i;
(3)i+i2+i3+…+i2017
=i?1?i+1+…+i
=i.
【解析】
【分析】
本题考查了新定义问题,能读懂题意是解此题的关键,主要考查了学生的理解能力和计算能力,难度适中.
(1)把i2=?1代入求出即可;
(2)根据多项式乘以多项式的计算法则进行计算,再把i2=?1代入求出即可;
(3)先根据复数的定义计算,再合并即可求解.
【解答】
解:(1)i3=i2?i=?i,i4=(i2)2=(?1)2=1.
故答案为:?i,1;
(2)见答案;
(3)见答案.
25.【答案】(1)(a?b)2? ?,(a+b)2?4ab? ;
(2)?(a+b)2?4ab=(a?b)2? ;
问题解决:由(2)得(x?y)2=(x+y)2?4xy.
∵x+y=6,xy=5,
∴(x?y)2=36?20=16,
∴x?y=±4.
【解析】
【分析】
本题考查了完全平方公式的几何背景、正方形的面积以及长方形的面积,解题的关键是:(1)利用长方形、正方形的面积公式,找出结论;(2)由阴影部分的面积相等,找出(a+b)2?4ab=(a?b)2?;(问题解决)代入x+y=6,xy=5求出结论.
(1)图②中阴影部分为边长为(a?b)的正方形,利用正方形的面积公式可得出S阴影=(a?b)2;图②中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,利用正方形及长方形的面积公式可得出S阴影=(a+b)2?4ab;
(2)由阴影部分的面积相等可得出:(a+b)2?4ab=(a?b)2?;
问题解决:由(2)可得出(x?y)2=(x+y)2?4xy,代入x+y=6,xy=5开方后即可得出结论.
【解答】
解:(1)图②中阴影部分为边长为(a?b)的正方形,
∴S阴影=(a?b)2;
图②中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,
∴S阴影=(a+b)2?4ab.
故答案为:(a?b)2;(a+b)2?4ab.
(2)由(1)可知:(a+b)2?4ab=(a?b)2?.
故答案为:(a+b)2?4ab=(a?b)2?.
问题解决见答案.
第9章整式乘法与因式分解章节复习限时作业
一、选择题(本大题共8小题,共24.0分)
下列运算正确的是(????)
A. a2?a5=a10 B. (3a3)2=6a6
C. (a+b)2=a2+b2 D. (a+2)(a?3)=a2?a?6
计算(a?2)(a+3)的结果是(????)
A. a2?6 B. a2+a?6 C. a2+6 D. a2?a+6
下列各式由左到右的变形中,属于分解因式的是(????)
A. a(m+n)=am+an
B. a2?b2?c2=(a?b)(a+b)?c2
C. 10x2?5x=5x(2x?1)
D. x2?16+6x=(x+4)(x?4)+6x
若x+m与2?x的乘积中不含x的一次项,则实数m的值为(????)
A. ?2 B. 2 C. 0 D. 1
下列运算正确的是(????)
A. (?2a)2=?4a2 B. (a+b)2=a2+b2
C. (a5)2=a7 D. (?a+2)(?a?2)=a2?4
下列各式能用平方差公式计算的是(????)
A. (2a+b)(2b?a) B. (x+1)(?x?1)
C. (?m?n)(?m+n) D. (3x?y)(?3x+y)
若多项式a2+ka+9是完全平方式,则常数k的值为(????)
A. 6 B. 3 C. ±6 D. ±3
下面因式分解错误的是(????)
A. x2?y2=(x+y)(x?y) B. x2?8x+16=(x?4)2
C. 2x2?2xy=2x(x?y) D. x2+y2=(x+y)2
二、填空题(本大题共8小题,共24.0分)
已知a?2b=?2,则代数式a(b?2)?b(a?4)的值为______.
因式分解:3x3?12x=______.
若关于x的二次三项式x2+ax+14是完全平方式,则a的值是______.
已知:m?n=6,mn=1,则m2+n2=______.
若a?2b=3,则2a?4b?5=_________.
若?xa+by5与3x4y2b?a的和是单项式,则(2a+2b)(a?3b)的值为??????????.
已知a+b=10,a?b=8,则a2?b2=______.
如图,利用图①和图②的阴影面积相等,写出一个正确的等式______.
center0
三、计算题(本大题共5小题,共40.0分)
计算:
(1)?22+(?12)?2?(π?2)0?|?2| (2)(x?2y)(x+2y)?(x?2y)2.
分解因式:
(1)6xy2?9x2y?y3; (2)16x4?1.
先化简,再求值:(a+3)2?(a+1)(a?1)?2(2a+4),其中a=?12.
已知?(a+b)2=7,(a?b)2=3,求:
(1)ab的值.?????????
(2)a2+b2的值.
发现与探索.
(1)根据小明的解答将下列各式因式分解
小明的解答:a2?6a+5=a2?6a+9?9+5=(a?3)2?4=(a?5)(a?1)
①a2?12a+20
②(a?1)2?8(a?1)+7
③a2?6ab+5b2
(2)根据小丽的思考解决下列问题:
小丽的思考:代数式(a?3)2+4无论a取何值(a?3)2都大于等于0,再加上4,则代数式(a?3)2+4大于等于4,则(a?3)2+4有最小值为4.
①说明:代数式a2?12a+20的最小值为?16.
②请仿照小丽的思考解释代数式?(a+1)2+8的最大值为8,并求代数式?a2+12a?8的最大值.
四、解答题(本大题共4小题,共32.0分)
对于任意有理数a、b、c、d,我们规定符号(a,b)?(c,d)=ad?bc,
例如:(1,3)?(2,4)=1×4?2×3=?2.
(1)求(?2,3)?(4,5)的值为______;
(2)求(3a+1,a?2)?(a+2,a?3)的值,其中a2?4a+1=0.
甲、乙两人共同计算一道整式:(x+a)(2x+b),由于甲抄错了a的符号,得到的结果是2x2?7x+3,乙漏抄了第二个多项式中x的系数,得到的结果是x2+2x?3.
(1)求a,b的值;
(2)请计算这道题的正确结果.
阅读理解题:
定义:如果一个数的平方等于?1,记为i2=?1,这个数i叫做虚数单位,把形如a+bi(a,b为实数)的数叫做复数,其中a叫这个复数的实部,b叫做这个复数的虚部,它的加,减,乘法运算与整式的加,减,乘法运算类似.
例如计算:(2?i)+(5+3i)=(2+5)+(?1+3)i=7+2i;
(1+i)×(2?i)=1×2?i+2×i?i2=2+(?1+2)i+1=3+i;
根据以上信息,完成下列问题:
(1)填空:i3=______,i4=______;
(2)计算:(1+i)×(3?4i);
(3)计算:i+i2+i3+…+i2017.
动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:______,______;
(2)请写出三个代数式(a+b)2,(a?b)2,ab之间的一个等量关系:______;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=6,xy=5,求x?y的值.
center0
答案和解析
1.【答案】D
【解析】解:A、原式=a7,不符合题意;
B、原式=9a6,不符合题意;
C、原式=a2+2ab+b2,不符合题意;
D、原式=a2?a?6,符合题意,
故选:D.
各式计算得到结果,即可作出判断.
此题考查了整式的混合运算,熟练掌握运算法则是解本题的关键.
2.【答案】B
【解析】
【分析】
此题考查多项式的乘法,关键是根据多项式乘法的法则解答.
根据多项式的乘法解答即可.
【解答】
解:(a?2)(a+3)=a2+3a?2a?6=a2+a?6,
故选:B.
3.【答案】C
【解析】
【分析】
本题考查因式分解的概念,解题的关键是正确理解因式分解的概念,属于基础题.
根据因式分解的定义即可判断.
【解答】
解:A.该变形为去括号,故A不是因式分解;
B.该等式右边没有化为几个整式的乘积形式,故B不是因式分解;
C.符合因式分解定义,故C是因式分解;
D该等式右边没有化为几个整式的乘积形式,故D不是因式分解.
故选:C.
4.【答案】B
【解析】
【分析】
此题考查了多项式乘多项式,熟练掌握运算法则是解本题的关键.
根据多项式乘以多项式的法则,可表示为(a+b)(m+n)=am+an+bm+bn,计算即可.
【解答】
解:根据题意得:
(x+m)(2?x)=2x?x2+2m?mx=?x2+(2?m)x+2m,
∵x+m与2?x的乘积中不含x的一次项,
∴m=2;
故选:B.
5.【答案】D
【解析】
【分析】
此题考查整式的运算,掌握各运算法则是关键,还要注意符号的处理.
按照积的乘方运算、完全平方公式、幂的乘方、平方差公式分别计算,再选择.
【解答】
解:A.(?2a)2=4a2,故选项A不符合题意;
B.(a+b)2=a2+2ab+b2,故选项B不符合题意;
C.(a5)2=a10,故选项C不符合题意;
D.(?a+2)(?a?2)=a2?4,故选项D符合题意.
故选:D.
6.【答案】C
【解析】解:A、B、D都不是平方差公式;
C、(?m?n)(?m+n)=(?m)2?n2,故C正确;
故选:C.
根据两数和乘以这两个数的差等于这两个数的平方差,可得答案.
本题考查了平方差公式,利用了平方差公式.
7.【答案】C
【解析】解:∵a2+ka+9=a2+ka+32,
∴ka=±2×a×3,
解得k=±6.
故选为:C.
先根据两平方项确定出这两个数,再根据完全平方公式的乘积二倍项即可确定k的值.
本题主要考查了完全平方式,根据平方项确定出这两个数是解题的关键,也是难点,熟记完全平方公式对解题非常重要.
8.【答案】D
【解析】解:A、x2?y2=(x+y)(x?y),正确,不合题意;
B、x2?8x+16=(x?4)2,正确,不合题意;
C、2x2?2xy=2x(x?y),正确,不合题意;
D、x2+y2≠(x+y)2,此选项错误,符合题意.
故选:D.
分别利用完全平方公式以及平方差公式分解因式,进而判断得出答案.
此题主要考查了公式法以及提取公因式法分解因式,熟练应用乘法公式是解题关键.
9.【答案】4
【解析】解:a(b?2)?b(a?4)
=ab?2a?ab+4b
=?2a+4b
=?2(a?2b),
∵a?2b=?2,
∴原式=?2×(?2)=4.
故答案为:4.
直接利用单项式乘多项式计算,再把已知代入得出答案.
此题主要考查了单项式乘多项式,正确将原式变形是解题关键.
10.【答案】3x(x+2)(x?2)
【解析】解:3x3?12x
=3x(x2?4)
=3x(x+2)(x?2)
故答案是:3x(x+2)(x?2).
首先提公因式3x,然后利用平方差公式即可分解.
本题考查了提公因式法与公式法分解因式,要求灵活使用各种方法对多项式进行因式分解,一般来说,如果可以先提取公因式的要先提取公因式,再考虑运用公式法分解.
11.【答案】±1
【解析】解:中间一项为加上或减去x的系数和12积的2倍,
故a=±1,
解得a=±1,
故答案为:±1.
这里首末两项是x和12这两个数的平方,那么中间一项为加上或减去x的系数和12积的2倍,故?a=±1,求解即可
本题考查了完全平方式的应用,两数的平方和,再加上或减去它们积的2倍,就构成了一个完全平方式.关键是注意积的2倍的符号,避免漏解.
12.【答案】38
【解析】解:∵(m?n)2=m2+n2?2mn,
∵36=m2+n2?2,
∴m2+n2=38,
故答案为38.
根据完全平方公式(m?n)2=m2+n2?2mn即可解题.
本题考查了完全平方公式的运用,解题的关键是正确运用(m?n)2=m2+n2?2mn.
13.【答案】1
【解析】
【分析】
此题考查整式的化简求值,根据题意,将原式变形为2(a?2b)?5,然后用整体代入法求解即可.
【解答】
解:∵a?2b=3
∴原式=2a?2b?5=2×3?5=1
故答案为1?.
14.【答案】?64
【解析】
【分析】
此题考查了多项式乘多项式,以及合并同类项,熟练掌握同类项性质及运算法则是解本题的关键.根据题意得到两式为同类项,确定出a与b的值,代入原式计算即可求出值.
【解答】
解:∵?xa+by5与3x4y2b?a的和是单项式,
∴?xa+by5与3x4y2b?a为同类项,即
a+b=4?①
2b?a=5?②
①+②得b=3,再代入①得a=1,
则(2a+2b)(a?3b)=(2+6)×(1?9)=?64,
故答案为:?64
15.【答案】80
【解析】
【分析】
本题考查平方差公式,解题的关键是熟练运用平方差公式,本题属于基础题型.根据平方差公式即可求出答案.
【解答】
解:∵(a+b)(a?b)=a2?b2,a+b=10,a?b=8,
∴a2?b2=10×8=80.
故答案为80.
16.【答案】(a+2)(a?2)=a2?4
【解析】解:①阴影部分的面积=(a+2)(a?2);
②阴影部分的面积=a2?22=a2?4;
∴(a+2)(a?2)=a2?4,
故答案为(a+2)(a?2)=a2?4;
①阴影部分的面积=(a+2)(a?2);
②阴影部分的面积=a2?22=a2?4;即可求解.
本题考查平方差公式的几何背景;理解题意,结合图形面积的关系得到公式,并能灵活运用公式是解题的关键.
17.【答案】解:(1)原式=?4+4?1?2=?3;
(2)原式=x2?4y2?x2+4xy?4y2=4xy?8y2.
【解析】(1)原式利用零指数幂、负整数指数幂法则和绝对值的代数意义化简,计算即可得到结果;
(2)原式利用平方差公式以及完全平方公式化简,去括号合并即可得到结果.
本题考查了平方差公式以及完全平方公式,熟练掌握公式是解本题的关键.
18.【答案】解:(1)原式=?y(y2?6xy+9x2)
=?y(y?3x)2;
(2)原式=(4x2+1)(4x2?1)
=(4x2+1)(2x+1)(2x?1).
【解析】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.
(1)原式提取公因式,再利用完全平方公式分解即可;
(2)原式利用平方差公式分解即可.
19.【答案】解:
原式=a2+6a+9?(a2?1)?4a?8
=2a+2
将a=?12代入原式=2×(?12)+2=1
【解析】注意到(a+3)2可以利用完全平方公式进行展开,(a+1)(a?1)利润平方差公式可化为(a2?1),则将各项合并即可化简,最后代入a=?12进行计算.
本题主要考查整式的混合运算,灵活运用两条乘法公式:完全平方公式和平方差公式是解题的关键,同时,在去括号的过程中要注意括号前的符号,若为负号,去括号后,括号里面的符号要改变
20.【答案】解:(1)∵(a+b)2=a2+2ab+b2=7①,(a?b)2=a2?2ab+b2=3②,
∴①?②得:4ab=4,即ab=1;
(2)①+②得:2(a2+b2)=10,即a2+b2=5.
【解析】利用完全平方公式将已知等式左边展开,分别记作①和②,
(1)①?②后,即可求出ab的值;(2)①+②,整理即可求出a2+b2的值.
此题考查了完全平方公式的运用,熟练掌握完全平方公式是解本题的关键.
21.【答案】解:(1)①a2?12a+20
=a2?12a+36?36+20
=(a?6)2?42
=(a?10)(a?2);
②(a?1)2?8(a?1)+12
=(a?1)2?8(a?1)+16?16+12
=(a?5)2?22
=(a?7)(a?3);
③a2?6ab+5b2
=a2?6ab+9b2?9b2+5b2
=(a?3b)2?4b2
=(a?5b)(a?b);
(2)①a2?12a+20
=a2?12a+36?36+20
=(a?6)2?16,
无论a取何值(a?6)2都大于等于0,再加上?16,
则代数式(a?6)2?16大于等于?16,
则a2?12a+20的最小值为?16;
②无论a取何值?(a+1)2都小于等于0,再加上8,
则代数式?(a+1)2+8小于等于8,
则?(a+1)2+8的最大值为8,
?a2+12a?8.
=?(a2?12a+8)
=?(a2?12a+36?36+8)
=?(a?6)2+36?8
=?(a?6)2+28
无论a取何值?(a?6)2都小于等于0,再加上28,
则代数式?(a?6)2+28小于等于28,
则?a2+12a?8的最大值为28.
【解析】本题考查的是因式分解的应用、偶次方的非负性,掌握完全平方公式、平方差公式、偶次方的非负性是解题的关键.
(1)仿照小明的解答过程、利用完全平方公式、平方差公式计算;
(2)仿照小丽的思考过程,利用完全平方公式、平方差公式计算、偶次方的非负性解答.
22.【答案】(1)?22;
(2)(3a+1,a?2)?(a+2,a?3)
=(3a+1)(a?3)?(a?2)(a+2)
=3a2?9a+a?3?(a2?4)
=3a2?9a+a?3?a2+4
=2a2?8a+1,
∵a2?4a+1=0,
∴a2=4a?1,
∴3a+1,a?2)?(a+2,a?3)=2(4a?1)?8a+1=?1.
【解析】解:(1)(?2,3)?(4,5)=?2×5?3×4=?10?12=?22;
故答案为:?22;
(2)见答案.
(1)利用新定义得到(?2,3)?(4,5)=?2×5?3×4,然后进行有理数的混合运算即可;
(2)利用新定义得到原式=(3a+1)(a?3)?(a?2)(a+2),然后去括号后合并,最后利用整体代入的方法计算.
本题考查了整式的混合运算?化简求值:先按运算顺序把整式化简,再把对应字母的值代入求整式的值.有乘方、乘除的混合运算中,要按照先乘方后乘除的顺序运算,其运算顺序和有理数的混合运算顺序相似.
23.【答案】解:(1)由题意,得(x?a)(2x+b)=2x2?7x+3,
2x2+(b?2a)x?ab=2x2?7x+3,
得b?2a=?7,
(x+a)(x+b)=x2+2x?3,
x2+(a+b)x+ab=x2+2x?3,
得a+b=2,
由b?2a=?7a+b=2,
得a=3b=?1,
(2)把a=3b=?1代入整式(x+a)(2x+b),得
(x+3)(2x?1)
=2x2?x+6x?3,
=2x2+5x?3.
【解析】此题考查了多项式乘多项式,解题的关键是根据多项式乘多项式的运算法则分别进行计算,是常考题型,解题时要细心.
(1)先按甲、乙错误的说法得出关于a、b的二元一次方程组,求出a,b的值;
(2)把a,b的值代入原式求出整式乘法的正确结果.
24.【答案】解:(1)?i;1;
(2)(1+i)×(3?4i)
=3?4i+3i?4i2
=3?i+4
=7?i;
(3)i+i2+i3+…+i2017
=i?1?i+1+…+i
=i.
【解析】
【分析】
本题考查了新定义问题,能读懂题意是解此题的关键,主要考查了学生的理解能力和计算能力,难度适中.
(1)把i2=?1代入求出即可;
(2)根据多项式乘以多项式的计算法则进行计算,再把i2=?1代入求出即可;
(3)先根据复数的定义计算,再合并即可求解.
【解答】
解:(1)i3=i2?i=?i,i4=(i2)2=(?1)2=1.
故答案为:?i,1;
(2)见答案;
(3)见答案.
25.【答案】(1)(a?b)2? ?,(a+b)2?4ab? ;
(2)?(a+b)2?4ab=(a?b)2? ;
问题解决:由(2)得(x?y)2=(x+y)2?4xy.
∵x+y=6,xy=5,
∴(x?y)2=36?20=16,
∴x?y=±4.
【解析】
【分析】
本题考查了完全平方公式的几何背景、正方形的面积以及长方形的面积,解题的关键是:(1)利用长方形、正方形的面积公式,找出结论;(2)由阴影部分的面积相等,找出(a+b)2?4ab=(a?b)2?;(问题解决)代入x+y=6,xy=5求出结论.
(1)图②中阴影部分为边长为(a?b)的正方形,利用正方形的面积公式可得出S阴影=(a?b)2;图②中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,利用正方形及长方形的面积公式可得出S阴影=(a+b)2?4ab;
(2)由阴影部分的面积相等可得出:(a+b)2?4ab=(a?b)2?;
问题解决:由(2)可得出(x?y)2=(x+y)2?4xy,代入x+y=6,xy=5开方后即可得出结论.
【解答】
解:(1)图②中阴影部分为边长为(a?b)的正方形,
∴S阴影=(a?b)2;
图②中阴影部分可看成在边长为(a+b)的正方形中减去4个长为a、宽为b的长方形,
∴S阴影=(a+b)2?4ab.
故答案为:(a?b)2;(a+b)2?4ab.
(2)由(1)可知:(a+b)2?4ab=(a?b)2?.
故答案为:(a+b)2?4ab=(a?b)2?.
问题解决见答案.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
