2020-2021学年鲁教版五四制数学六年级下册期末测试卷(一)(含答案)
文档属性
| 名称 | 2020-2021学年鲁教版五四制数学六年级下册期末测试卷(一)(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-28 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
鲁教版五四制数学六年级下册期末测试(一)
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.下列四个图形中,∠1与∠2是对顶角的是( )
2下列运算正确的是( )
A.a3·a4=a12 B.(-a4)3=a12 C.(2y2)3=6y6 D.a12÷a2=a10
3.过点B画线段AC所在直线的垂线段,其中正确的是( )
4.如图,下列说法错误的是( )
A.∠A与∠C是同旁内角 B.∠1与∠3是同位角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
5.下列问题中,不适合采用普查的是( )
A.了解本班学生对数学老师的满意度 B.“嫦娥三号”发射前对各部件的检查
C.调查八年级三班所有学生的身高情况 D.了解“DF-21”对航空母舰的杀伤力
6.赵悦同学从家骑自行车上,一开始以某一速度行进,途中车子发生故障,只好停下来修车,车修好后,因怕耽误上课,于是就加快了速度,s为赵悦离家的距离,t为赵悦离家的时间,则下列能表示s关于t的关系的是( )
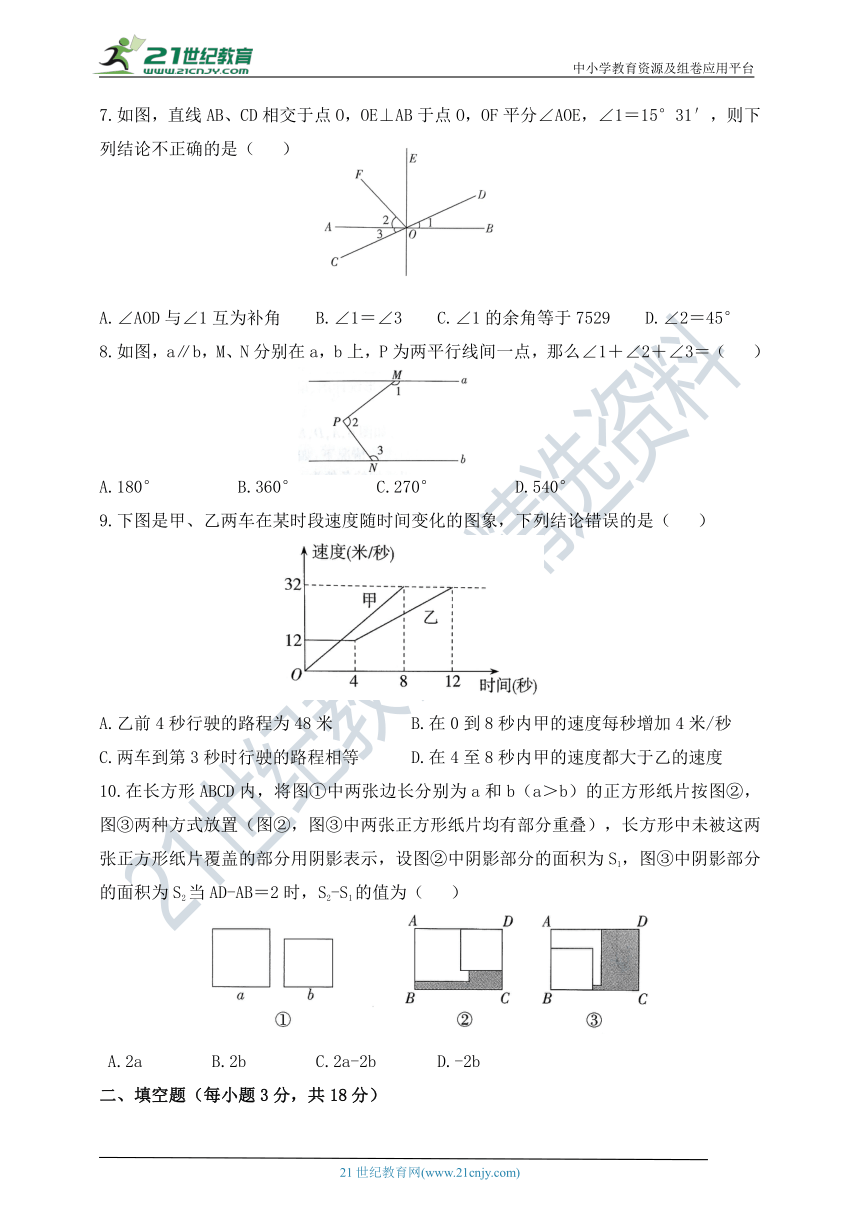
7.如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°31′,则下列结论不正确的是( )
A.∠AOD与∠1互为补角 B.∠1=∠3 C.∠1的余角等于7529 D.∠2=45°
8.如图,a∥b,M、N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180° B.360° C.270° D.540°
9.下图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米 B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等 D.在4至8秒内甲的速度都大于乙的速度
10.在长方形ABCD内,将图①中两张边长分别为a和b(a>b)的正方形纸片按图②,图③两种方式放置(图②,图③中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图②中阴影部分的面积为S1,图③中阴影部分的面积为S2当AD-AB=2时,S2-S1的值为( )
A.2a B.2b C.2a-2b D.-2b
二、填空题(每小题3分,共18分)
11.计算:___________.
12.2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于0.000 000 02秒,则0.000 000 02用科学记数法表示为____________.
13.随着国家计划生育政策的改变,家庭人口的组成也发生了改变某城市家庭人口数的一次统计结果表明:2口之家占20%,3口之家占50%,四口之家占20%,5口之家占10%,选用_______________来反映这些数据最合适(从折线统计图、条形统计图、扇形统计图中选一个).
14.如图,A,D,E三点在同一条直线上,在不添加辅助线的情况下,如果添加一个条件,使AB∥CD,则可以添加的条件为_____________.(任意添加一个符合题意的条件即可)
15.已知线段AB=10 cm,点D是线段AB的中点,直线AB上有一点C,并且BC=2 cm,则线段DC的长为____________.
16.下图是由同样大小的圆按一定规律排列组成的,第1个图形中一共有4个圆,第2个图形中一共有8个圆,第3个图形中一共有14个圆,第4个图形中一共有22个圆……按此规律排列下去,第9个图形中圆的个数是___________.
三、解答题(共62分)
17.(9分)
(1)计算:;
(2)计算:(a-b)3·(a-b)2·(b-a);
(3)先化简,再求值:3a(2a+b)-(a+3b)(a-3b),其中a=1,b=-.
18.(10分)如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.
19.(10分)在“一带一路”的倡议下,我国已成为设施联通、贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,图9是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图:
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?补全条形统计图;
(3)求扇形统计图中陆运货物量对应的扇形圆心角的度数.
20.(10分)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又返回到刚经过的某书店,买到书后继续去学校.图10是他本次上学所用的时间与离家距离的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的距离是多少米?小明在书店停留了多少分钟?
(2)上学途中,小明一共骑行了多少米?一共用了多少分钟?
(3)在整个上学的途中,哪个时间段小明骑车的速度最快?最快的速度是多少?
(4)小明出发多长时间离家的距离为1200米?
21.(10分)如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发,以1cm/s、3cm/s的速度沿直线BA向左运动.
(1)若AB=10cm,2m<AM<4cm,当点C、D运动了2s时,求AC+MD的值;
(2)若点C、D在运动过程中,总有MD=3AC,则AM=________AB;
(3)如图②,若AM=AB,点N是直线AB上一点,且AN-BN=MN,求的值.
22.(13分)已知AB∥CD,∠ABE与∠CDE的平分线相交于点F.
(1)如图①,若∠E=80°,求∠BFD的度数;
(2)如图②,若∠ABM=∠ABF,∠CDM=∠CDF,试写出∠M与∠E之间的数量关系,并证明你的结论;
(3)如图②,若∠ABM=∠ABF,∠CDM=∠CDF,∠E=m,请直接用含有n,m的式子表示出∠M.
参考答案
一、选择题
1.D 2.D 3.D 4.B 5.D 6.B 7.C 8.B 9.C 10.B
二、填空题
11. -2019 12. 2×10-8 13.扇形统计图 14.答案不唯一,如∠A=∠EDC
15. 7 cm或3 cm 16. 92
三、解答题
17.解析(1)原式=-8x7y5÷(-x4y3)=16x3y2.
(2)原式=(a-b)3·(a-b)2·[-(a-b)]=-(a-b)6.
(3)原式=6a2+3ab-(a2-9b2)=5a2+3ab+9b2.
当a=1,b=-时,原式=5×12+3×1×(-)+9×(-)2=5.
18.解析 设∠COE=a,则∠BOE=2a,所以∠BOC=3a,
因为∠FOE=90°,所以∠BOF=90°+2a,
又因为OC平分∠BOF,所以∠BOC=∠BOF=45°+a,
所以3a=45°+a,解得a=22.5°,
所以∠BOC=67.5°,所以∠BOD=180°-∠BOC=112.5°.
19.解析 (1)该物流园2016年货运总量是120÷50%=240(万吨).
(2)该物流园2016年空运货物的总量是240×15%=36(万吨),补全条形统计图如图所示.
(3)扇形统计图中陆运货物量对应的扇形圆心角的度数为360°×(1-50%-30%-15%)=18°.
20.解析 (1)小明家到学校的距离是1500米,小明在书店停留了12-8=4(分钟).
(2)上学途中,小明一共骑行了1500+(200-600)×2=2700(米),一共用了14分钟.
(3)在整个上学的途中,12分钟至14分钟小明骑车的速度最快,最快的速度为(1500-600)÷(14-12)=450米/分钟.
(4)设t分钟时,小明离家的距离为1200米,
由题图得t=6或t-12=(1200-600)÷450,∴t=6或t=13,
故小明出发6分钟或13分钟时离家的距离为1200米.
21.解析 (1)当点C、D运动了2s时,CM=2cm,BD=6 cm.
因为AB=10cm,CM=2cm,BD=6cm,
所以AC+MD=AB-CM-BD=10-2-6=2cm.
(2)因为C,D两点的速度分别为1cm/s,3cm/s,所以BD=3CM.
又因为MD=3AC,所以BD+MD=3CM+3AC,即BM=3AM,所以AM=AB.
(3)当点N在线段AB上时,如图1,
因为AN-BN=MN,又因为AN-AM=MN,所以BN=AM=AB,
所以MN=AB,即.
当点N在线段AB的延长线上时,如图2,
因为AN-BN=MN,又因为AN-BN=AB,所以MN=AB,即=1.
综上所述,或1.
22.解析(1)如图,过E作EG∥AB,过F作FH∥AB,
因为AB∥CD,所以EG∥AB∥FH∥CD.
所以∠ABF=∠BFH,∠CDF=∠DFH,∠BE+∠BEG=180°,∠GED+∠CDE=180°,
所以∠ABE+∠BEG+∠GED+∠CDE=360°.
因为∠BED=∠BEG+∠DEG=80°,所以∠ABE+∠CDE=280°.
因为∠ABE和∠CDE的平分线相交于点F,所以∠ABF+∠CDF=140°.
所以∠BFD=∠BFH+∠DFH=140°.
(2)6∠M+∠E=360°.
证明:因为∠ABM=∠ABF,∠CDM=∠CDF,所以∠ABF=3∠ABM,∠CDF=3∠CDM,
因为∠ABE与∠CDE的平分线相交于点F,所以∠ABE=6∠ABM,∠CDE=6∠CDM,
所以6∠ABM+6∠CDM+∠E=360°.
易知∠M=∠ABM+∠CDM,所以6∠M+∠E=360°.
(3)由(2)的结论可得2n∠ABM+2n∠CDM+∠E=360°,∠M=∠ABM+∠CDM,
所以∠M=.
_21?????????è?????(www.21cnjy.com)_
鲁教版五四制数学六年级下册期末测试(一)
(时间:100分钟 满分:120分)
一、选择题(每小题4分,共40分)
1.下列四个图形中,∠1与∠2是对顶角的是( )
2下列运算正确的是( )
A.a3·a4=a12 B.(-a4)3=a12 C.(2y2)3=6y6 D.a12÷a2=a10
3.过点B画线段AC所在直线的垂线段,其中正确的是( )
4.如图,下列说法错误的是( )
A.∠A与∠C是同旁内角 B.∠1与∠3是同位角
C.∠2与∠3是内错角 D.∠3与∠B是同旁内角
5.下列问题中,不适合采用普查的是( )
A.了解本班学生对数学老师的满意度 B.“嫦娥三号”发射前对各部件的检查
C.调查八年级三班所有学生的身高情况 D.了解“DF-21”对航空母舰的杀伤力
6.赵悦同学从家骑自行车上,一开始以某一速度行进,途中车子发生故障,只好停下来修车,车修好后,因怕耽误上课,于是就加快了速度,s为赵悦离家的距离,t为赵悦离家的时间,则下列能表示s关于t的关系的是( )
7.如图,直线AB、CD相交于点O,OE⊥AB于点O,OF平分∠AOE,∠1=15°31′,则下列结论不正确的是( )
A.∠AOD与∠1互为补角 B.∠1=∠3 C.∠1的余角等于7529 D.∠2=45°
8.如图,a∥b,M、N分别在a,b上,P为两平行线间一点,那么∠1+∠2+∠3=( )
A.180° B.360° C.270° D.540°
9.下图是甲、乙两车在某时段速度随时间变化的图象,下列结论错误的是( )
A.乙前4秒行驶的路程为48米 B.在0到8秒内甲的速度每秒增加4米/秒
C.两车到第3秒时行驶的路程相等 D.在4至8秒内甲的速度都大于乙的速度
10.在长方形ABCD内,将图①中两张边长分别为a和b(a>b)的正方形纸片按图②,图③两种方式放置(图②,图③中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图②中阴影部分的面积为S1,图③中阴影部分的面积为S2当AD-AB=2时,S2-S1的值为( )
A.2a B.2b C.2a-2b D.-2b
二、填空题(每小题3分,共18分)
11.计算:___________.
12.2020年6月23日9时43分,“北斗三号”最后一颗全球组网卫星发射成功,它的授时精度小于0.000 000 02秒,则0.000 000 02用科学记数法表示为____________.
13.随着国家计划生育政策的改变,家庭人口的组成也发生了改变某城市家庭人口数的一次统计结果表明:2口之家占20%,3口之家占50%,四口之家占20%,5口之家占10%,选用_______________来反映这些数据最合适(从折线统计图、条形统计图、扇形统计图中选一个).
14.如图,A,D,E三点在同一条直线上,在不添加辅助线的情况下,如果添加一个条件,使AB∥CD,则可以添加的条件为_____________.(任意添加一个符合题意的条件即可)
15.已知线段AB=10 cm,点D是线段AB的中点,直线AB上有一点C,并且BC=2 cm,则线段DC的长为____________.
16.下图是由同样大小的圆按一定规律排列组成的,第1个图形中一共有4个圆,第2个图形中一共有8个圆,第3个图形中一共有14个圆,第4个图形中一共有22个圆……按此规律排列下去,第9个图形中圆的个数是___________.
三、解答题(共62分)
17.(9分)
(1)计算:;
(2)计算:(a-b)3·(a-b)2·(b-a);
(3)先化简,再求值:3a(2a+b)-(a+3b)(a-3b),其中a=1,b=-.
18.(10分)如图,直线AB,CD交于点O,将一个三角板的直角顶点放置于点O处,使其两条直角边分别位于OC的两侧.若OC刚好平分∠BOF,∠BOE=2∠COE,求∠BOD的度数.
19.(10分)在“一带一路”的倡议下,我国已成为设施联通、贸易畅通的促进者,同时也带动了我国与沿线国家的货物交换的增速发展,图9是湘成物流园2016年通过“海、陆(汽车)、空、铁”四种模式运输货物的统计图:
请根据统计图解决下面的问题:
(1)该物流园2016年货运总量是多少万吨?
(2)该物流园2016年空运货物的总量是多少万吨?补全条形统计图;
(3)求扇形统计图中陆运货物量对应的扇形圆心角的度数.
20.(10分)小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又返回到刚经过的某书店,买到书后继续去学校.图10是他本次上学所用的时间与离家距离的关系示意图.根据图中提供的信息回答下列问题:
(1)小明家到学校的距离是多少米?小明在书店停留了多少分钟?
(2)上学途中,小明一共骑行了多少米?一共用了多少分钟?
(3)在整个上学的途中,哪个时间段小明骑车的速度最快?最快的速度是多少?
(4)小明出发多长时间离家的距离为1200米?
21.(10分)如图①,已知点M是线段AB上一点,点C在线段AM上,点D在线段BM上,C、D两点分别从M、B出发,以1cm/s、3cm/s的速度沿直线BA向左运动.
(1)若AB=10cm,2m<AM<4cm,当点C、D运动了2s时,求AC+MD的值;
(2)若点C、D在运动过程中,总有MD=3AC,则AM=________AB;
(3)如图②,若AM=AB,点N是直线AB上一点,且AN-BN=MN,求的值.
22.(13分)已知AB∥CD,∠ABE与∠CDE的平分线相交于点F.
(1)如图①,若∠E=80°,求∠BFD的度数;
(2)如图②,若∠ABM=∠ABF,∠CDM=∠CDF,试写出∠M与∠E之间的数量关系,并证明你的结论;
(3)如图②,若∠ABM=∠ABF,∠CDM=∠CDF,∠E=m,请直接用含有n,m的式子表示出∠M.
参考答案
一、选择题
1.D 2.D 3.D 4.B 5.D 6.B 7.C 8.B 9.C 10.B
二、填空题
11. -2019 12. 2×10-8 13.扇形统计图 14.答案不唯一,如∠A=∠EDC
15. 7 cm或3 cm 16. 92
三、解答题
17.解析(1)原式=-8x7y5÷(-x4y3)=16x3y2.
(2)原式=(a-b)3·(a-b)2·[-(a-b)]=-(a-b)6.
(3)原式=6a2+3ab-(a2-9b2)=5a2+3ab+9b2.
当a=1,b=-时,原式=5×12+3×1×(-)+9×(-)2=5.
18.解析 设∠COE=a,则∠BOE=2a,所以∠BOC=3a,
因为∠FOE=90°,所以∠BOF=90°+2a,
又因为OC平分∠BOF,所以∠BOC=∠BOF=45°+a,
所以3a=45°+a,解得a=22.5°,
所以∠BOC=67.5°,所以∠BOD=180°-∠BOC=112.5°.
19.解析 (1)该物流园2016年货运总量是120÷50%=240(万吨).
(2)该物流园2016年空运货物的总量是240×15%=36(万吨),补全条形统计图如图所示.
(3)扇形统计图中陆运货物量对应的扇形圆心角的度数为360°×(1-50%-30%-15%)=18°.
20.解析 (1)小明家到学校的距离是1500米,小明在书店停留了12-8=4(分钟).
(2)上学途中,小明一共骑行了1500+(200-600)×2=2700(米),一共用了14分钟.
(3)在整个上学的途中,12分钟至14分钟小明骑车的速度最快,最快的速度为(1500-600)÷(14-12)=450米/分钟.
(4)设t分钟时,小明离家的距离为1200米,
由题图得t=6或t-12=(1200-600)÷450,∴t=6或t=13,
故小明出发6分钟或13分钟时离家的距离为1200米.
21.解析 (1)当点C、D运动了2s时,CM=2cm,BD=6 cm.
因为AB=10cm,CM=2cm,BD=6cm,
所以AC+MD=AB-CM-BD=10-2-6=2cm.
(2)因为C,D两点的速度分别为1cm/s,3cm/s,所以BD=3CM.
又因为MD=3AC,所以BD+MD=3CM+3AC,即BM=3AM,所以AM=AB.
(3)当点N在线段AB上时,如图1,
因为AN-BN=MN,又因为AN-AM=MN,所以BN=AM=AB,
所以MN=AB,即.
当点N在线段AB的延长线上时,如图2,
因为AN-BN=MN,又因为AN-BN=AB,所以MN=AB,即=1.
综上所述,或1.
22.解析(1)如图,过E作EG∥AB,过F作FH∥AB,
因为AB∥CD,所以EG∥AB∥FH∥CD.
所以∠ABF=∠BFH,∠CDF=∠DFH,∠BE+∠BEG=180°,∠GED+∠CDE=180°,
所以∠ABE+∠BEG+∠GED+∠CDE=360°.
因为∠BED=∠BEG+∠DEG=80°,所以∠ABE+∠CDE=280°.
因为∠ABE和∠CDE的平分线相交于点F,所以∠ABF+∠CDF=140°.
所以∠BFD=∠BFH+∠DFH=140°.
(2)6∠M+∠E=360°.
证明:因为∠ABM=∠ABF,∠CDM=∠CDF,所以∠ABF=3∠ABM,∠CDF=3∠CDM,
因为∠ABE与∠CDE的平分线相交于点F,所以∠ABE=6∠ABM,∠CDE=6∠CDM,
所以6∠ABM+6∠CDM+∠E=360°.
易知∠M=∠ABM+∠CDM,所以6∠M+∠E=360°.
(3)由(2)的结论可得2n∠ABM+2n∠CDM+∠E=360°,∠M=∠ABM+∠CDM,
所以∠M=.
_21?????????è?????(www.21cnjy.com)_
同课章节目录
