18.2.1矩形第2课时 矩形的性质-2020-2021学年人教版八年级数学下册导学案(含详解)
文档属性
| 名称 | 18.2.1矩形第2课时 矩形的性质-2020-2021学年人教版八年级数学下册导学案(含详解) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 00:00:00 | ||
图片预览



文档简介
18.2.1矩形
第2课时 矩形的性质
学习目标:
知道直角三角形斜边中线的性质,并会进行简单的运用.
学习重点:直角三角形斜边中线的性质及其运用.
一、课前检测
已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.
求证:△AOB是等边三角形.(注意表达格式完整性与逻辑性)
拓展与延伸:本题若将“AC=2AB”改为“∠BOC=120°”,你能获得有关这个矩形的哪些结论?
二、温故知新
1.在Rt△ABC中,∠C=90°,∠A=30°,AB=10cm,则AC=______.
2.在Rt△ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
三、预习导航(预习教材第53页,标出你认为重要的关键词)
1.关于直角三角形,前面你有了哪些了解?
2.直角三角形斜边上的中线等于_______________.
用几何语言表示为:
四、自学自测
如图,矩形ABCD中,AB=2BC,且AB=AE,试求∠CBE的度数.
五、我的疑惑(反思)
要点探究
探究点1:直角三角形斜边上的中线的性质
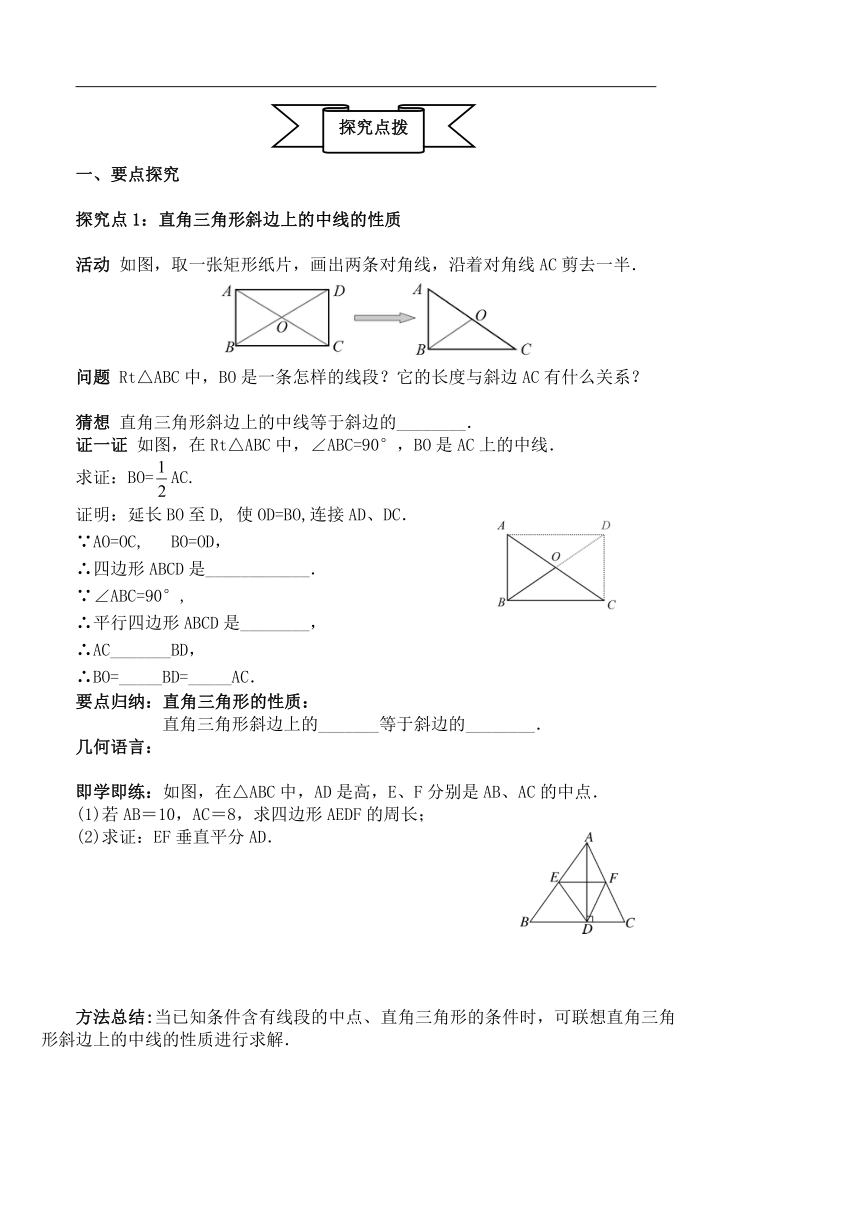
活动 如图,取一张矩形纸片,画出两条对角线,沿着对角线AC剪去一半.
问题 Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
猜想 直角三角形斜边上的中线等于斜边的________.
证一证 如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证:BO=AC.
证明:延长BO至D, 使OD=BO,连接AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是____________.
∵∠ABC=90°,
∴平行四边形ABCD是________,
∴AC_______BD,
∴BO=_____BD=_____AC.
要点归纳:直角三角形的性质:
直角三角形斜边上的_______等于斜边的________.
几何语言:
即学即练:如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
方法总结:当已知条件含有线段的中点、直角三角形的条件时,可联想直角三角形斜边上的中线的性质进行求解.
二、精讲点拨
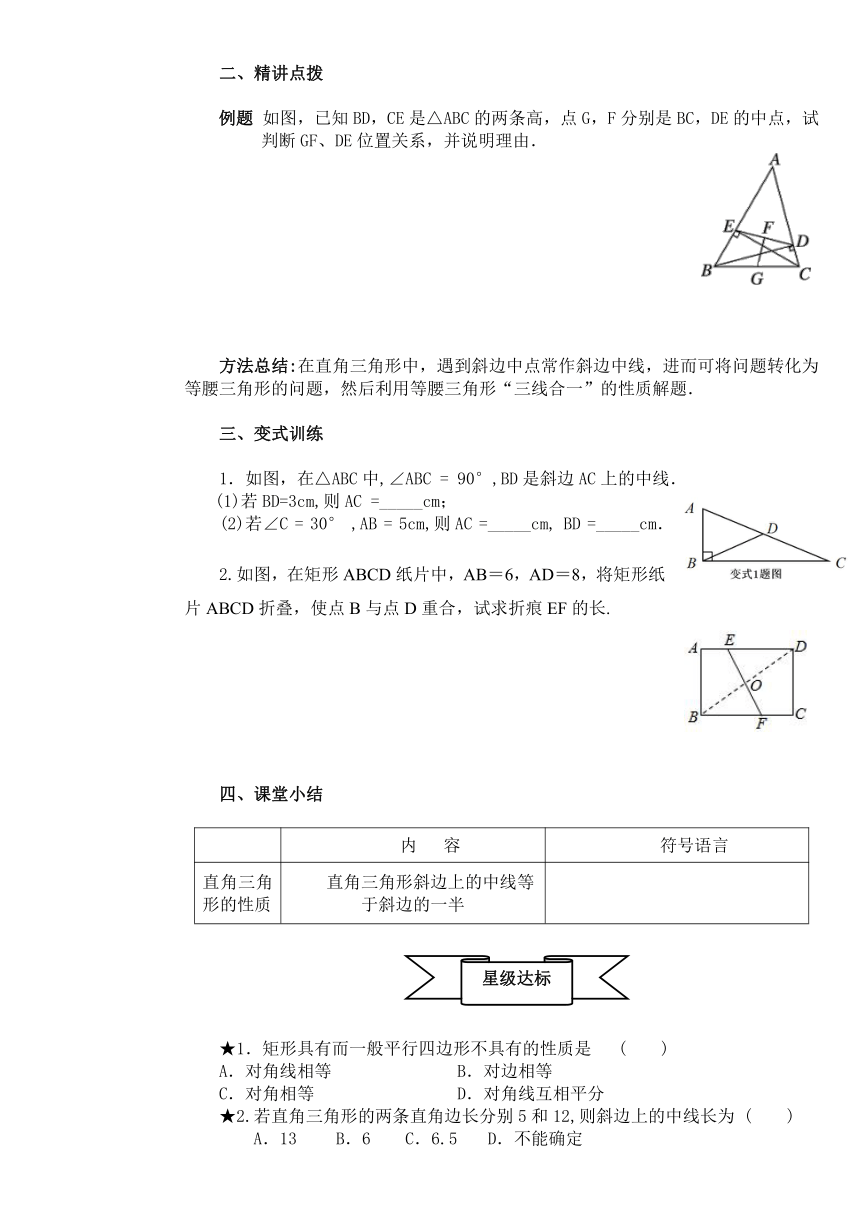
例题 如图,已知BD,CE是△ABC的两条高,点G,F分别是BC,DE的中点,试判断GF、DE位置关系,并说明理由.
方法总结:在直角三角形中,遇到斜边中点常作斜边中线,进而可将问题转化为等腰三角形的问题,然后利用等腰三角形“三线合一”的性质解题.
三、变式训练
1.如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3cm,则AC =_____cm;
(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD =_____cm.
2.如图,在矩形ABCD纸片中,AB=6,AD=8,将矩形纸片ABCD折叠,使点B与点D重合,试求折痕EF的长.
四、课堂小结
内 容 符号语言
直角三角形的性质 直角三角形斜边上的中线等于斜边的一半
★1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
★2.若直角三角形的两条直角边长分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
★3. 如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
★★4.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
★★5.如图,在△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=BE.求证:∠B=2∠BCE.
★★6.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4 ,求四边形ABED的面积.
★★★7.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.
我的反思(收获,不足)
分层作业
必做 (教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:根据矩形的对角线互相平分且相等可得OA=OB,再求出AB=AC,然后根据三条边都相等的三角形是等边三角形得证.
证明:△OAB是等边三角形.
理由如下:在矩形ABCD中,OA=OC,OB=OD,AC=BD,
∴OA=AC,OB=BD,
又∵AB=AC,
∴OA=OB=AB,
即△OAB是等边三角形.
拓展与延伸:本题若将“AC=2AB”改为“∠BOC=120°”获得的结论有:∠OAD=∠ODA=∠OBC=∠OCB=30°,AC=BD=2AB=2CD,△OAB,△OCD是等边三角形等.
证明略
温故知新
1.试题分析:根据30°角所对的直角边等于斜边的一半,即可求得AC的长.
详解:∵∠C=90°,∠B=30°,AB=10cm,
∴AC=AB=5,
故答案为:5.
2.试题分析:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,直角三角形两锐角互余,如图,取AB的中点D,连接CD,证明△ACD是等边三角形即可.
详解:如图,取AB的中点D,连接CD.
∵∠C=90°,AD=BD,
∴CD=AD=BD,
∵AB=2AC,
∴AC=AD=CD,
∴△ACD是等边三角形,
∴∠ADC=60°,
∵DC=DB,
∴∠B=∠DCB,
∵∠ADC=∠B+∠DCB,
∴∠B=30°,∴∠A=90°﹣∠B=90°﹣30°=60°.
自学自测
试题分析:根据矩形性质得出∠D=∠ABC=90°,AD=BC,DC∥AB,推出AE=2AD,得出∠DEA=30°=∠EAB,求出∠EBA的度数,即可求出答案.
详解:∵四边形ABCD是矩形,
∴∠D=∠ABC=90°,AD=BC,DC∥AB,
∵AB=AE,AB=2CB,
∴AE=2AD,
∴∠DEA=30°,
∵DC∥AB,
∴∠DEA=∠EAB=30°,
∵AE=AB,
∴∠ABE=∠AEB=(180°﹣∠EAB)=75°,
∵∠ABC=90°,∴∠EBC=90°﹣75°=15°.
即学即练:
试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得DE=AE=AB,DF=AF=AC,再根据四边形的周长的定义计算即可得解;
(2)根据到到线段两端点距离相等的点在线段的垂直平分线上证明即可.
详解:(1)∵AD是高,E、F分别是AB、AC的中点,
∴DE=AE=AB=×10=5,DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴E,F都在AD的垂直平分线上.
∴EF垂直平分AD.
精讲点拨
例题 试题分析:连接EG、FG,根据直角三角形斜边上的中线等于斜边的一半可得DG=EG=BC,再根据等腰三角形的三线合一证明即可.
证明:GF⊥DE.理由如下:
如图,连接EG、DG,
∵BD、CE分别是△ABC的AC、BC边上的高,点G是BC的中点,
∴DG=EG=BC,
∵点F是DE的中点,
∴GF⊥DE.
变式训练
1.试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半即可得出AC=2BD=6cm;
(2)先根据直角三角形30°角所对的直角边等于斜边的一半得出AC=2AB=10cm,再根据直角三角形斜边上的中线等于斜边的一半得出BD=AC=5cm.
详解:(1)∵Rt△ABC,∠ABC=90°,BD是斜边AC上的中线,BD=3cm,
∴AC=2BO=6cm;
∵Rt△ABC,∠ABC=90°,∠C = 30° ,AB = 5cm,
∴AC=2AB=10cm.
∵BD是斜边AC上的中线,
∴BD=AC=5cm.
故答案为(1)6;(2)10, 5.
2.试题分析:本题主要考查了轴对称变换,矩形的性质以及勾股定理的运用,连接BE,过E作EG⊥BC于G,设AE=x,根据勾股定理得到AE,进而得出BE的长,根据EG=AD,求出GF的长,运用勾股定理即可得到EF.
详解:连接BE,过E作EG⊥BC于G,
设AE=x,则DE=BE=8﹣x.
在Rt△ABE中,AB2+AE2=BE2,
∴x2+62=(8﹣x)2
解得x=, ∴AE=.
∴BE=DE=8﹣=,
∵∠DEF=∠BFE,∠DEF=∠BEF,
∴∠BFE=∠BEF,
∴BF=BE=,
∴GF=,
∴Rt△EFG中,EF==,
即EF的长为.
星级达标:
1.试题分析:由矩形的性质和平行四边形的性质即可得出结论.
详解:∵矩形的对边相等,对角相等,对角线互相平分且相等;
平行四边形的对边相等,对角相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:A.
2.试题分析:根据勾股定理可求得直角三角形斜边的长,再根据直角三角形斜边上的中线等于斜边的一半即可求解.
详解:∵直角三角形两直角边长为5和12,
∴斜边==13,
∴此直角三角形斜边上的中线的长==6.5.
故选:C.
3.试题分析:由BE⊥AC,D为AB中点,DE=5,根据直角三角形斜边的中线等于斜边的一半,即可求得AB的长,然后由勾股定理求得BE的长.
详解:∵BE⊥AC,∴∠AEB=90°,
∵D为AB中点,
∴AB=2DE=2×5=10,
∵AE=8,
∴BE==6.
故答案为:6.
4.试题分析:本题考查了勾股定理,矩形性质,三角形中位线的应用,关键是求出OD长.根据勾股定理求出AC,根据矩形性质得出∠ABC=90°,BD=AC,BO=OD,求出BD、OD,根据三角形中位线性质即可得解.
详解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=6cm,BC=8cm,
∴由勾股定理得:BD=AC==10(cm),
∴DO=5cm,
∵点E、F分别是AO、AD的中点,
∴EF=OD=2.5cm,
故答案为:2.5.
5.试题分析:根据直角三角形斜边上中线性质推出DE=BE=CD,根据等腰三角形性质推出∠B=∠EDB,∠BCE=∠DEC,根据三角形外角性质即可推出答案.
证明:连接ED.
∵AD是高,∴∠ADB=90°,
在Rt△ADB中,DE是AB边上的中线,
∴ED=,
∴∠B=∠EDB.
∵DC=BE,
∴ED=DC,
∴∠DEC=∠ECD,
∵∠EDB=∠DEC+∠ECD=2∠BCE,
∴∠B=2∠BCE.
6.试题分析:(1)根据矩形的对角线相等可得AC=BD,然后证明四边形ABEC是平行四边形,再根据平行四边形的对边相等可得AC=BE,从而得证;
(2)根据矩形的对角线互相平分求出BD的长度,再根据30°角所对的直角边等于斜边的一半求出CD的长度,然后利用勾股定理求出BC的长度,再利用梯形的面积公式列式计算即可得解.
详解:(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
(2)解:∵在矩形ABCD中,BO=4,
∴BD=2BO=2×4=8,
∵∠DBC=30°,
∴CD=BD=×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=4+4=8,
在Rt△BCD中,BC===4,
∴四边形ABED的面积=(4+8)×4=24.
7.试题分析:本题考查了矩形的判定和性质、勾股定理、三角形面积、垂线段最短等知识,解题的关键是熟练掌握基本知识.由勾股定理求出BC的长,再证明四边形DMAN是矩形,可得MN=AD,根据垂线段最短和三角形面积即可解决问题.
详解:线段MN存在最小值.
∵∠BAC=90°,且BA=3,AC=4,
∴BC==5,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD==,
∴MN的最小值为.
第2课时 矩形的性质
学习目标:
知道直角三角形斜边中线的性质,并会进行简单的运用.
学习重点:直角三角形斜边中线的性质及其运用.
一、课前检测
已知:如图,矩形ABCD的两条对角线相交于点O,且AC=2AB.
求证:△AOB是等边三角形.(注意表达格式完整性与逻辑性)
拓展与延伸:本题若将“AC=2AB”改为“∠BOC=120°”,你能获得有关这个矩形的哪些结论?
二、温故知新
1.在Rt△ABC中,∠C=90°,∠A=30°,AB=10cm,则AC=______.
2.在Rt△ABC中,∠C=90°,AB=2AC,求∠A、∠B的度数.
三、预习导航(预习教材第53页,标出你认为重要的关键词)
1.关于直角三角形,前面你有了哪些了解?
2.直角三角形斜边上的中线等于_______________.
用几何语言表示为:
四、自学自测
如图,矩形ABCD中,AB=2BC,且AB=AE,试求∠CBE的度数.
五、我的疑惑(反思)
要点探究
探究点1:直角三角形斜边上的中线的性质
活动 如图,取一张矩形纸片,画出两条对角线,沿着对角线AC剪去一半.
问题 Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
猜想 直角三角形斜边上的中线等于斜边的________.
证一证 如图,在Rt△ABC中,∠ABC=90°,BO是AC上的中线.
求证:BO=AC.
证明:延长BO至D, 使OD=BO,连接AD、DC.
∵AO=OC, BO=OD,
∴四边形ABCD是____________.
∵∠ABC=90°,
∴平行四边形ABCD是________,
∴AC_______BD,
∴BO=_____BD=_____AC.
要点归纳:直角三角形的性质:
直角三角形斜边上的_______等于斜边的________.
几何语言:
即学即练:如图,在△ABC中,AD是高,E、F分别是AB、AC的中点.
(1)若AB=10,AC=8,求四边形AEDF的周长;
(2)求证:EF垂直平分AD.
方法总结:当已知条件含有线段的中点、直角三角形的条件时,可联想直角三角形斜边上的中线的性质进行求解.
二、精讲点拨
例题 如图,已知BD,CE是△ABC的两条高,点G,F分别是BC,DE的中点,试判断GF、DE位置关系,并说明理由.
方法总结:在直角三角形中,遇到斜边中点常作斜边中线,进而可将问题转化为等腰三角形的问题,然后利用等腰三角形“三线合一”的性质解题.
三、变式训练
1.如图,在△ABC中,∠ABC = 90°,BD是斜边AC上的中线.
(1)若BD=3cm,则AC =_____cm;
(2)若∠C = 30° ,AB = 5cm,则AC =_____cm, BD =_____cm.
2.如图,在矩形ABCD纸片中,AB=6,AD=8,将矩形纸片ABCD折叠,使点B与点D重合,试求折痕EF的长.
四、课堂小结
内 容 符号语言
直角三角形的性质 直角三角形斜边上的中线等于斜边的一半
★1.矩形具有而一般平行四边形不具有的性质是 ( )
A.对角线相等 B.对边相等
C.对角相等 D.对角线互相平分
★2.若直角三角形的两条直角边长分别5和12,则斜边上的中线长为 ( )
A.13 B.6 C.6.5 D.不能确定
★3. 如图,△ABC中,E在AC上,且BE⊥AC.D为AB中点,若DE=5,AE=8,则BE的长为______.
★★4.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD的中点,若AB=6cm,BC=8cm,则EF=______cm.
★★5.如图,在△ABC中,AD是BC边上的高,CE是AB边上的中线,且DC=BE.求证:∠B=2∠BCE.
★★6.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.(1)求证:BD=BE;
(2)若∠DBC=30°,BO=4 ,求四边形ABED的面积.
★★★7.如图,在Rt△ABC中,∠BAC=90°,且BA=3,AC=4,点D是斜边BC上的一个动点,过D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN是否存在最小值?若存在,求出其最小值;若不存在,请说明理由.
我的反思(收获,不足)
分层作业
必做 (教材 智慧学习 配套) 选做
参考答案:
课前检测
试题分析:根据矩形的对角线互相平分且相等可得OA=OB,再求出AB=AC,然后根据三条边都相等的三角形是等边三角形得证.
证明:△OAB是等边三角形.
理由如下:在矩形ABCD中,OA=OC,OB=OD,AC=BD,
∴OA=AC,OB=BD,
又∵AB=AC,
∴OA=OB=AB,
即△OAB是等边三角形.
拓展与延伸:本题若将“AC=2AB”改为“∠BOC=120°”获得的结论有:∠OAD=∠ODA=∠OBC=∠OCB=30°,AC=BD=2AB=2CD,△OAB,△OCD是等边三角形等.
证明略
温故知新
1.试题分析:根据30°角所对的直角边等于斜边的一半,即可求得AC的长.
详解:∵∠C=90°,∠B=30°,AB=10cm,
∴AC=AB=5,
故答案为:5.
2.试题分析:本题考查了直角三角形30°角所对的直角边等于斜边的一半的性质,直角三角形两锐角互余,如图,取AB的中点D,连接CD,证明△ACD是等边三角形即可.
详解:如图,取AB的中点D,连接CD.
∵∠C=90°,AD=BD,
∴CD=AD=BD,
∵AB=2AC,
∴AC=AD=CD,
∴△ACD是等边三角形,
∴∠ADC=60°,
∵DC=DB,
∴∠B=∠DCB,
∵∠ADC=∠B+∠DCB,
∴∠B=30°,∴∠A=90°﹣∠B=90°﹣30°=60°.
自学自测
试题分析:根据矩形性质得出∠D=∠ABC=90°,AD=BC,DC∥AB,推出AE=2AD,得出∠DEA=30°=∠EAB,求出∠EBA的度数,即可求出答案.
详解:∵四边形ABCD是矩形,
∴∠D=∠ABC=90°,AD=BC,DC∥AB,
∵AB=AE,AB=2CB,
∴AE=2AD,
∴∠DEA=30°,
∵DC∥AB,
∴∠DEA=∠EAB=30°,
∵AE=AB,
∴∠ABE=∠AEB=(180°﹣∠EAB)=75°,
∵∠ABC=90°,∴∠EBC=90°﹣75°=15°.
即学即练:
试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半可得DE=AE=AB,DF=AF=AC,再根据四边形的周长的定义计算即可得解;
(2)根据到到线段两端点距离相等的点在线段的垂直平分线上证明即可.
详解:(1)∵AD是高,E、F分别是AB、AC的中点,
∴DE=AE=AB=×10=5,DF=AF=AC=×8=4,
∴四边形AEDF的周长=AE+DE+DF+AF=5+5+4+4=18;
(2)证明:∵DE=AE,DF=AF,
∴E,F都在AD的垂直平分线上.
∴EF垂直平分AD.
精讲点拨
例题 试题分析:连接EG、FG,根据直角三角形斜边上的中线等于斜边的一半可得DG=EG=BC,再根据等腰三角形的三线合一证明即可.
证明:GF⊥DE.理由如下:
如图,连接EG、DG,
∵BD、CE分别是△ABC的AC、BC边上的高,点G是BC的中点,
∴DG=EG=BC,
∵点F是DE的中点,
∴GF⊥DE.
变式训练
1.试题分析:(1)根据直角三角形斜边上的中线等于斜边的一半即可得出AC=2BD=6cm;
(2)先根据直角三角形30°角所对的直角边等于斜边的一半得出AC=2AB=10cm,再根据直角三角形斜边上的中线等于斜边的一半得出BD=AC=5cm.
详解:(1)∵Rt△ABC,∠ABC=90°,BD是斜边AC上的中线,BD=3cm,
∴AC=2BO=6cm;
∵Rt△ABC,∠ABC=90°,∠C = 30° ,AB = 5cm,
∴AC=2AB=10cm.
∵BD是斜边AC上的中线,
∴BD=AC=5cm.
故答案为(1)6;(2)10, 5.
2.试题分析:本题主要考查了轴对称变换,矩形的性质以及勾股定理的运用,连接BE,过E作EG⊥BC于G,设AE=x,根据勾股定理得到AE,进而得出BE的长,根据EG=AD,求出GF的长,运用勾股定理即可得到EF.
详解:连接BE,过E作EG⊥BC于G,
设AE=x,则DE=BE=8﹣x.
在Rt△ABE中,AB2+AE2=BE2,
∴x2+62=(8﹣x)2
解得x=, ∴AE=.
∴BE=DE=8﹣=,
∵∠DEF=∠BFE,∠DEF=∠BEF,
∴∠BFE=∠BEF,
∴BF=BE=,
∴GF=,
∴Rt△EFG中,EF==,
即EF的长为.
星级达标:
1.试题分析:由矩形的性质和平行四边形的性质即可得出结论.
详解:∵矩形的对边相等,对角相等,对角线互相平分且相等;
平行四边形的对边相等,对角相等,对角线互相平分;
∴矩形具有而平行四边形不具有的性质是对角线相等;
故选:A.
2.试题分析:根据勾股定理可求得直角三角形斜边的长,再根据直角三角形斜边上的中线等于斜边的一半即可求解.
详解:∵直角三角形两直角边长为5和12,
∴斜边==13,
∴此直角三角形斜边上的中线的长==6.5.
故选:C.
3.试题分析:由BE⊥AC,D为AB中点,DE=5,根据直角三角形斜边的中线等于斜边的一半,即可求得AB的长,然后由勾股定理求得BE的长.
详解:∵BE⊥AC,∴∠AEB=90°,
∵D为AB中点,
∴AB=2DE=2×5=10,
∵AE=8,
∴BE==6.
故答案为:6.
4.试题分析:本题考查了勾股定理,矩形性质,三角形中位线的应用,关键是求出OD长.根据勾股定理求出AC,根据矩形性质得出∠ABC=90°,BD=AC,BO=OD,求出BD、OD,根据三角形中位线性质即可得解.
详解:∵四边形ABCD是矩形,
∴∠ABC=90°,BD=AC,BO=OD,
∵AB=6cm,BC=8cm,
∴由勾股定理得:BD=AC==10(cm),
∴DO=5cm,
∵点E、F分别是AO、AD的中点,
∴EF=OD=2.5cm,
故答案为:2.5.
5.试题分析:根据直角三角形斜边上中线性质推出DE=BE=CD,根据等腰三角形性质推出∠B=∠EDB,∠BCE=∠DEC,根据三角形外角性质即可推出答案.
证明:连接ED.
∵AD是高,∴∠ADB=90°,
在Rt△ADB中,DE是AB边上的中线,
∴ED=,
∴∠B=∠EDB.
∵DC=BE,
∴ED=DC,
∴∠DEC=∠ECD,
∵∠EDB=∠DEC+∠ECD=2∠BCE,
∴∠B=2∠BCE.
6.试题分析:(1)根据矩形的对角线相等可得AC=BD,然后证明四边形ABEC是平行四边形,再根据平行四边形的对边相等可得AC=BE,从而得证;
(2)根据矩形的对角线互相平分求出BD的长度,再根据30°角所对的直角边等于斜边的一半求出CD的长度,然后利用勾股定理求出BC的长度,再利用梯形的面积公式列式计算即可得解.
详解:(1)证明:∵四边形ABCD是矩形,
∴AC=BD,AB∥CD,
又∵BE∥AC,
∴四边形ABEC是平行四边形,
∴AC=BE,
∴BD=BE.
(2)解:∵在矩形ABCD中,BO=4,
∴BD=2BO=2×4=8,
∵∠DBC=30°,
∴CD=BD=×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=4+4=8,
在Rt△BCD中,BC===4,
∴四边形ABED的面积=(4+8)×4=24.
7.试题分析:本题考查了矩形的判定和性质、勾股定理、三角形面积、垂线段最短等知识,解题的关键是熟练掌握基本知识.由勾股定理求出BC的长,再证明四边形DMAN是矩形,可得MN=AD,根据垂线段最短和三角形面积即可解决问题.
详解:线段MN存在最小值.
∵∠BAC=90°,且BA=3,AC=4,
∴BC==5,
∵DM⊥AB,DN⊥AC,
∴∠DMA=∠DNA=∠BAC=90°,
∴四边形DMAN是矩形,
∴MN=AD,
∴当AD⊥BC时,AD的值最小,
此时,△ABC的面积=AB×AC=BC×AD,
∴AD==,
∴MN的最小值为.
