2020-2021学年北师大版九下数学课堂检测附答案第3章 4 圆周角和圆心角的关系(word版含解析)
文档属性
| 名称 | 2020-2021学年北师大版九下数学课堂检测附答案第3章 4 圆周角和圆心角的关系(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 444.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-29 13:13:56 | ||
图片预览

文档简介
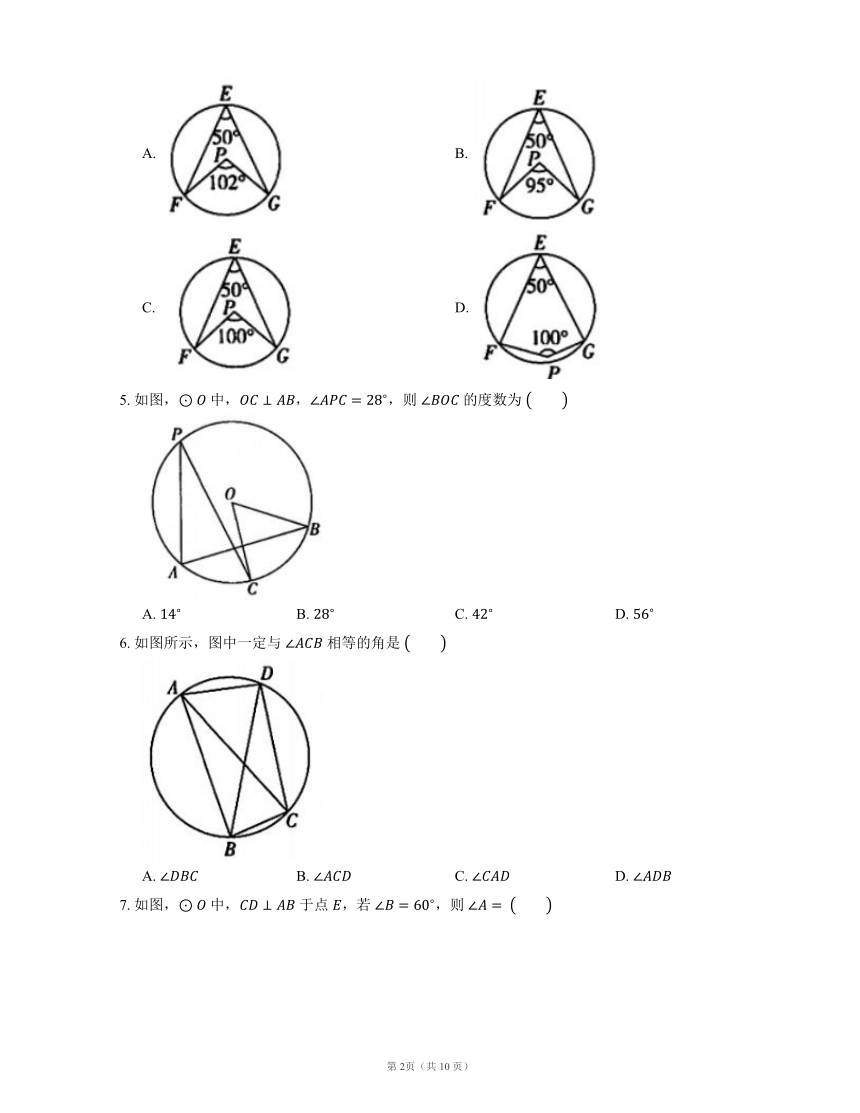
北师大版九下数学第3章
4
圆周角和圆心角的关系
一、选择题(共11小题;共66分)
1.
如图,,,
三点在
上,,则
的度数为
A.
B.
C.
D.
2.
如图,,
为
的两条弦,,则
的度数为
A.
B.
C.
D.
3.
下列图形中,
为圆周角的是
A.
B.
C.
D.
4.
已知
,,
为圆上的三点,,则下列四个选项中,
点可能是圆心的是
A.
B.
C.
D.
5.
如图,
中,,,则
的度数为
A.
B.
C.
D.
6.
如图所示,图中一定与
相等的角是
A.
B.
C.
D.
7.
如图,
中,
于点
,若
,则
A.
B.
C.
D.
8.
如图,
是
上一点,
是直径,,,点
在
上且平分
,则
的长为
A.
B.
C.
D.
9.
如图,若
是
的直径,
是
的弦,,则
的度数为
A.
B.
C.
D.
10.
如图所示,四边形
为
的内接四边形,,则
的大小是
A.
B.
C.
D.
11.
如图,由边长为
的小正方形构成的网格中,点
,,
都在格点上,以
为直径的圆经过点
,,则
的值为
A.
B.
C.
D.
二、填空题(共3小题;共15分)
12.
如图,有一圆形展厅,在其圆形边缘上的点
处安装了一台监视器,它的监控角度是
,为了监控整个展厅,最少需在圆形边缘上安装
?台这样的监视器.
13.
如图,点
,,,
分别在
上,,若
,则
的度数是
?.
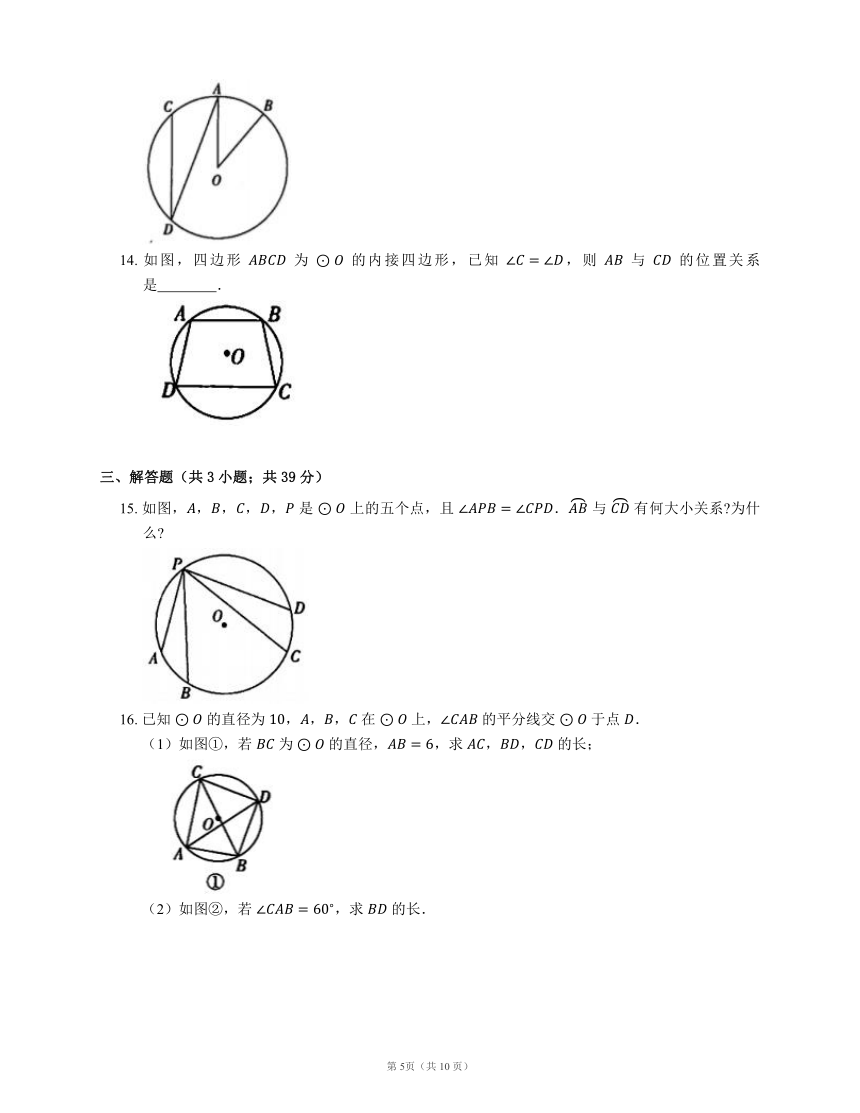
14.
如图,四边形
为
的内接四边形,已知
,则
与
的位置关系是
?.
三、解答题(共3小题;共39分)
15.
如图,,,,,
是
上的五个点,且
.
与
有何大小关系?为什么?
16.
已知
的直径为
,,,
在
上,
的平分线交
于点
.
(1)如图①,若
为
的直径,,求
,,
的长;
(2)如图②,若
,求
的长.
17.
如图,
的内接四边形
的两组对边的延长线分别交于点
,.
(1)若
,则
?
.
(2)当
,
时,求
的度数.
答案
第一部分
1.
A
【解析】,
.
2.
B
【解析】如图在优弧
上取点
,连接
,,
由圆周角定理得,,
由圆内接四边形的性质得,,
,
,
解得
.
3.
A
【解析】依据圆周角的概念来判断,点
必须在圆上,边
,
必须分别与圆还有另一个交点,故选A.
4.
C
【解析】若
点为圆心,则
.
观察C、D易知C符合题意.
5.
D
【解析】连接
,
因为在
中,,
所以
,
因为
,
所以
.
6.
D
【解析】
所对的弧是
,此弧所对的圆周角还有
,
与
相等的角是
.
7.
A
【解析】,
,
,
.
8.
D
【解析】
点
在
上且平分
,
,
,
是
的直径,
,
,,
,
在
中,,
,
(舍负).
故选D.
9.
A
【解析】如图,连接
,
为直径,
.
,
,
.
10.
B
【解析】
四边形
为
的内接四边形,,
,
由圆周角定理得
.故选B.
11.
A
【解析】如图,连接
,,
和
所对的弧都是
,
根据圆周角定理知,,
在
中,
,,
,
根据锐角三角函数的定义知,,
.故选A.
第二部分
12.
【解析】监视器的监控角度是
,即圆周角
,根据圆周角等于它所对弧上的圆心角的一半,可知对应的圆心角为
,因为
,所以要监控整个展厅,最少需在圆形边缘上安装
台这样的监视器.
13.
【解析】连接
,
,
,
.
14.
【解析】
四边形
为圆内接四边形,
,
又
,
,
.
第三部分
15.
与
相等.理由如下:
如图,连接
,,,,
,
,
.
16.
(1)
为
的直径,
,
在
中,,,
,
平分
,
,
,
在
中,,,,
.
??????(2)
如图,连接
,,
平分
,,
,
,
又
,
是等边三角形,
.
的直径为
,
,
.
17.
(1)
【解析】,,,,
.
四边形
是
的内接四边形,
,
.
??????(2)
在
中,,,
,
,
在
中,.
第6页(共10
页)
4
圆周角和圆心角的关系
一、选择题(共11小题;共66分)
1.
如图,,,
三点在
上,,则
的度数为
A.
B.
C.
D.
2.
如图,,
为
的两条弦,,则
的度数为
A.
B.
C.
D.
3.
下列图形中,
为圆周角的是
A.
B.
C.
D.
4.
已知
,,
为圆上的三点,,则下列四个选项中,
点可能是圆心的是
A.
B.
C.
D.
5.
如图,
中,,,则
的度数为
A.
B.
C.
D.
6.
如图所示,图中一定与
相等的角是
A.
B.
C.
D.
7.
如图,
中,
于点
,若
,则
A.
B.
C.
D.
8.
如图,
是
上一点,
是直径,,,点
在
上且平分
,则
的长为
A.
B.
C.
D.
9.
如图,若
是
的直径,
是
的弦,,则
的度数为
A.
B.
C.
D.
10.
如图所示,四边形
为
的内接四边形,,则
的大小是
A.
B.
C.
D.
11.
如图,由边长为
的小正方形构成的网格中,点
,,
都在格点上,以
为直径的圆经过点
,,则
的值为
A.
B.
C.
D.
二、填空题(共3小题;共15分)
12.
如图,有一圆形展厅,在其圆形边缘上的点
处安装了一台监视器,它的监控角度是
,为了监控整个展厅,最少需在圆形边缘上安装
?台这样的监视器.
13.
如图,点
,,,
分别在
上,,若
,则
的度数是
?.
14.
如图,四边形
为
的内接四边形,已知
,则
与
的位置关系是
?.
三、解答题(共3小题;共39分)
15.
如图,,,,,
是
上的五个点,且
.
与
有何大小关系?为什么?
16.
已知
的直径为
,,,
在
上,
的平分线交
于点
.
(1)如图①,若
为
的直径,,求
,,
的长;
(2)如图②,若
,求
的长.
17.
如图,
的内接四边形
的两组对边的延长线分别交于点
,.
(1)若
,则
?
.
(2)当
,
时,求
的度数.
答案
第一部分
1.
A
【解析】,
.
2.
B
【解析】如图在优弧
上取点
,连接
,,
由圆周角定理得,,
由圆内接四边形的性质得,,
,
,
解得
.
3.
A
【解析】依据圆周角的概念来判断,点
必须在圆上,边
,
必须分别与圆还有另一个交点,故选A.
4.
C
【解析】若
点为圆心,则
.
观察C、D易知C符合题意.
5.
D
【解析】连接
,
因为在
中,,
所以
,
因为
,
所以
.
6.
D
【解析】
所对的弧是
,此弧所对的圆周角还有
,
与
相等的角是
.
7.
A
【解析】,
,
,
.
8.
D
【解析】
点
在
上且平分
,
,
,
是
的直径,
,
,,
,
在
中,,
,
(舍负).
故选D.
9.
A
【解析】如图,连接
,
为直径,
.
,
,
.
10.
B
【解析】
四边形
为
的内接四边形,,
,
由圆周角定理得
.故选B.
11.
A
【解析】如图,连接
,,
和
所对的弧都是
,
根据圆周角定理知,,
在
中,
,,
,
根据锐角三角函数的定义知,,
.故选A.
第二部分
12.
【解析】监视器的监控角度是
,即圆周角
,根据圆周角等于它所对弧上的圆心角的一半,可知对应的圆心角为
,因为
,所以要监控整个展厅,最少需在圆形边缘上安装
台这样的监视器.
13.
【解析】连接
,
,
,
.
14.
【解析】
四边形
为圆内接四边形,
,
又
,
,
.
第三部分
15.
与
相等.理由如下:
如图,连接
,,,,
,
,
.
16.
(1)
为
的直径,
,
在
中,,,
,
平分
,
,
,
在
中,,,,
.
??????(2)
如图,连接
,,
平分
,,
,
,
又
,
是等边三角形,
.
的直径为
,
,
.
17.
(1)
【解析】,,,,
.
四边形
是
的内接四边形,
,
.
??????(2)
在
中,,,
,
,
在
中,.
第6页(共10
页)
