初三数学九下二次函数讲学案
图片预览



文档简介
初三数学(九下 )第二章二次函数讲学案
内容解读
二次函数的概念。
二次函数的图像及性质。
二次函数与一元二次方程、一元二次不等式的联系。
二次函数的应用
能力解读
会用描点法画出二次函数的图像,能从图像上认识二次函数的性质。
会根据公式确定图像的顶点、开口方向和对称轴。
会根据抛物线确定a、b、c的符号。
4.会用配方法把抛物线的解析式化为 的形式。
5.能利用二次函数解决简单的实际问题。
趋势方法
命题趋势
考察二次此函数的图像与性质,通过对实际问题情境的分析,确定二次函数的表达式并体会二次函数的意义,能用数形结合,归纳等数学思想,根据二次函数的表达式{图像}确定二次函数的开口方向,对称轴和顶点坐标,待定系数法求函数解析式。从图像反映的函数性质,求解析式中字母的取值范围等。
2011年,多个省市设计了以点、线、图形运动为基础的开放性探究题,有的在图形变化过程中,探索两个变量之间的关系,并能根据实际情况确定自变量的取值范围,进而探求符合条件的图形的性质或点的坐标。也有的让学生通过迁移探索在新的条件下结论是否仍然成立,展示信息中变与不变的辩证关系。
2012年可能延续2011年命题方向,继续在二次函数的应用性、探究性方面进行探索。
突破方法
正确理解和掌握二次函数的概念、图像、性质。
利用数形结合思想,借助函数图像及性质,形象直观的解决有关不等式最大(小)值、方程的解及图形位置关系等问题。
利用转化思想,通过一元二次方程根的判别式及根与系数的关系来解决抛物线与x轴交点的问题。
知识清单
常考点清单
1.形如y=ax2+bx+c(a、b、c为常数)的函数,当a≠0时是二次函数;当a ,b≠时是一次函数。
2. 二次函数y=ax2+bx+c(a≠0)图像是对称轴平行于y轴(或重合)的一条抛物线;对称轴是x= ,顶点坐标是(,)。
3.当a>0时,抛物线y= ax2+bx+c(a≠0)开口向上,当x=时,函数的最小值是 ;在对称轴左侧,y随 x的增大而减小,在对称轴右侧,y随x的增大而 。
当a<0时,抛物线y= ax2+bx+c(a≠0)开口向下,当x=时,函数的最大值是 ;在对称轴左侧,y随 x的增大而 ,在对称轴右侧,y随x的增大而 。
4.抛物线 可有 的图像平移而得到。
5. 抛物线y= ax2+bx+c(a≠0)与x轴有两个交点,则一元二次方程ax2+bx+c=0(a≠0)有 实数根 。
6. 抛物线y= ax2+bx+c(a≠0)与x轴有一个公共点,则一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根。
7. 抛物线y= ax2+bx+c(a≠0)与x轴无交点,则一元二次方程ax2+bx+c=0(a≠0) 实数根。
2011年中考题组
一、选择题(每小题3分,共30分)
1.如果y=(m-2)x是关于x的二次函数,则m=( )
A.-1 B.2 C.-1或2 D.m不存在
2.对于抛物线y=x2+2和y=x2的论断:①开口方向相同;②形状完全相同;③对称轴相同.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
3.y=x2-7x-5与y轴的交点坐标为( )
A.-5 B.(0,-5) C.(-5,0) D.(0,-20)
4.下列函数一定是关于x的二次函数的是( )
A.y=ax+bx+c B.y=x+bx+c
C.y=(a2+a)x2+bx+c D.y=(a2-a)x2+bx+c
5.下列函数关系中,可以看作二次函数y=ax2+bx+c(a≠0)模型的是( )
A.在一定距离内,汽车行驶的速度与行驶的时间的关系
B.我国人口的自然增长率为1%,这样我国总人口数随年份变化的关系
C.矩形周长一定时,矩形面积和矩形边长之间的关系
D.圆的周长与半径之间的关系
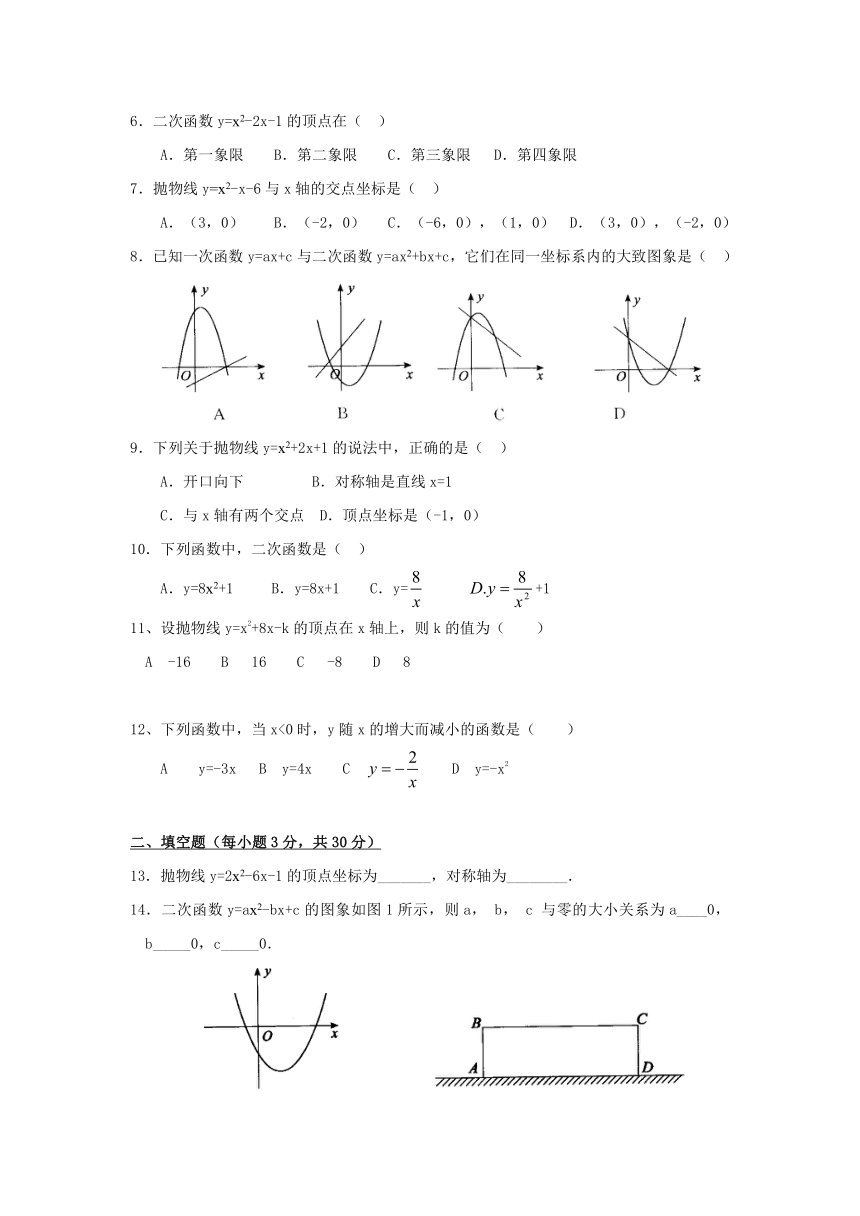
6.二次函数y=x2-2x-1的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.抛物线y=x2-x-6与x轴的交点坐标是( )
A.(3,0) B.(-2,0) C.(-6,0),(1,0) D.(3,0),(-2,0)
8.已知一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系内的大致图象是( )
9.下列关于抛物线y=x2+2x+1的说法中,正确的是( )
A.开口向下 B.对称轴是直线x=1
C.与x轴有两个交点 D.顶点坐标是(-1,0)
10.下列函数中,二次函数是( )
A.y=8x2+1 B.y=8x+1 C.y= HYPERLINK "http://" +1
11、设抛物线y=x2+8x-k的顶点在x轴上,则k的值为( )
A -16 B 16 C -8 D 8
12、下列函数中,当x<0时,y随x的增大而减小的函数是( )
A y=-3x B y=4x C D y=-x2
二、填空题(每小题3分,共30分) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
13.抛物线y=2x2-6x-1的顶点坐标为_______,对称轴为________.
14.二次函数y=ax2-bx+c的图象如图1所示,则a,b,c与零的大小关系为a____0,b_____0,c_____0.
( http: / / )
(1) (2)
15.若抛物线y=(m-1)x2+2mx+2m-1的图象的最低点的纵坐标为零,则m=_____.
16.已知二次函数y=ax2-4x-13a有最小值-17,则a=______.
17.二次函数y=x2+2的图象开口_______,对称轴是______,顶点坐标是_______.
18.如图2,用长60米的篱笆,靠墙围成一个长方形场地,在表示场地面积时,可以设_______为x米,也可以选择_______为x米,相应地面积S的解析式为_____或______.
19.抛物线y=x2+2x+4的图象可以看作是将y=x的图象经过_________平移得到的.
20.使函数y=x2-3x+2的值为零的x的值为_______.
21.函数y=2-3x2的图象,开口方向是________,对称轴是________,顶点坐标是_________.
22.无论m为任何实数,总在抛物线y=x2+2mx+m上的点是________.
三、解答下列各题(每题8分,共40分) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
23.已知抛物线y=x2-2ax+2a+b在x轴上截得的线段长为3,并且此抛物线的顶点坐标满足关系式:y=-x2,求a、b的值.
24.已知:如图所示,在△ABC中,BC=20,高AD=16,内接矩形EFGH的顶点E、F在BC上,G、H分别在AC、AB上,求内接矩形EFGH的最大面积.
25.已知正方形ABCD的边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶点的内接正方形的面积为y,求y与x的函数关系式,当x为何值时,内接正方形的面积最小?
26.已知一个二次函数y=ax2+bx+c的图象如图所示,请求出这个二次函数的关系式.
( http: / / )
27.某商店经营一种水产品,成本为每千克40元,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请回答下列问题:
(1)当销售单价为每千克55元时,计算销售量和月利润.
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式.
(3)销售单价定为多少元时,获得的利润最多?
28、已知抛物线的顶点为(1,-1),且过点(2,1),求这个函数的表达
29、已知一个二次函数的图象经过点(1,-1),(0,1),(-1,13),求这个二次函数的解析式;
30、已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上, 分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
(1)用含y的代数式表示AE.
(2)求y与x之间的函数关系式,并求出x的取值范围.
(3)设四边形DECF的面积为S,求出S的最大值.
标准答案
1.A 解析:令m2-m=2,解得m=2或m=-1,而m=2不合适,舍去.
2.D
3.B 解析:令x=0,求出y的值为-5.
4.B 5.C
6.D 解析:将二次函数进行配方为y=(x-1)2-2,顶点坐标为(1,-2).
7.D 解析:令y=0,求出x的值为-2与3,故交点坐标为(3,0),(-2,0).
8.C 9.D
10.A 解析:紧扣定义中的形式,B为一次函数,C为反比例函数,D虽是函数,但不是二次函数.11、A 12、A
13.(,-) x= 解析:将y=2x-6x-1配方为y=2(x- HYPERLINK "http://" )2-.
14.> < < 15. 16.1, 17.向上 y轴 (0,2)
18.AB BC S=-2x2+60x或S=-x2+30x
19.向左平移1个单位,再向上平移3个单位
20.1,2 21.向下 y轴 (0,2)
22.(,) 解:将y=x2+2mx+m进行整理得到y=x2+(2x+1)m,为使不受m的限制, 令2x+1=0,得出x=-,从而y=.
23.解:由题意知,抛物线的对称轴为x= HYPERLINK "http://" =a,
抛物线与x轴交点的横坐标为a-,a+.
抛物线的解析式也可以写成y=[x-(a-)][x-(a+)]=x2-2ax+a2-,
所以a2-=2a+b,令x=a,则y=- HYPERLINK "http://" ,所以顶点坐标为(a,-).
由于顶点坐标满足y=-x2,所以-=-a2,
故a=±,又2a+b=a2-=0,所以b=-2a,
所以a=,b=-3;或a=-,b=3.
24.80
25.y=2x2-8x+16.当x=2时,内接正方形的面积最小.
26.y=-x2+ HYPERLINK "http://" x+1
27.(1)450千克,6 750元;
(2)y=-10x2+1 400x-40 000;
(3)销售单价定为70元时,获得的利润最多是9 000元. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
30、(1)由已知得DECF是矩形,故EC=DF=y,AE=8-EC=8-y.
(2)∵DE∥BC,∴△ADE∽△ABC,∴,即.
∴y=8-2x(0D
C
B
F
E
A
内容解读
二次函数的概念。
二次函数的图像及性质。
二次函数与一元二次方程、一元二次不等式的联系。
二次函数的应用
能力解读
会用描点法画出二次函数的图像,能从图像上认识二次函数的性质。
会根据公式确定图像的顶点、开口方向和对称轴。
会根据抛物线确定a、b、c的符号。
4.会用配方法把抛物线的解析式化为 的形式。
5.能利用二次函数解决简单的实际问题。
趋势方法
命题趋势
考察二次此函数的图像与性质,通过对实际问题情境的分析,确定二次函数的表达式并体会二次函数的意义,能用数形结合,归纳等数学思想,根据二次函数的表达式{图像}确定二次函数的开口方向,对称轴和顶点坐标,待定系数法求函数解析式。从图像反映的函数性质,求解析式中字母的取值范围等。
2011年,多个省市设计了以点、线、图形运动为基础的开放性探究题,有的在图形变化过程中,探索两个变量之间的关系,并能根据实际情况确定自变量的取值范围,进而探求符合条件的图形的性质或点的坐标。也有的让学生通过迁移探索在新的条件下结论是否仍然成立,展示信息中变与不变的辩证关系。
2012年可能延续2011年命题方向,继续在二次函数的应用性、探究性方面进行探索。
突破方法
正确理解和掌握二次函数的概念、图像、性质。
利用数形结合思想,借助函数图像及性质,形象直观的解决有关不等式最大(小)值、方程的解及图形位置关系等问题。
利用转化思想,通过一元二次方程根的判别式及根与系数的关系来解决抛物线与x轴交点的问题。
知识清单
常考点清单
1.形如y=ax2+bx+c(a、b、c为常数)的函数,当a≠0时是二次函数;当a ,b≠时是一次函数。
2. 二次函数y=ax2+bx+c(a≠0)图像是对称轴平行于y轴(或重合)的一条抛物线;对称轴是x= ,顶点坐标是(,)。
3.当a>0时,抛物线y= ax2+bx+c(a≠0)开口向上,当x=时,函数的最小值是 ;在对称轴左侧,y随 x的增大而减小,在对称轴右侧,y随x的增大而 。
当a<0时,抛物线y= ax2+bx+c(a≠0)开口向下,当x=时,函数的最大值是 ;在对称轴左侧,y随 x的增大而 ,在对称轴右侧,y随x的增大而 。
4.抛物线 可有 的图像平移而得到。
5. 抛物线y= ax2+bx+c(a≠0)与x轴有两个交点,则一元二次方程ax2+bx+c=0(a≠0)有 实数根 。
6. 抛物线y= ax2+bx+c(a≠0)与x轴有一个公共点,则一元二次方程ax2+bx+c=0(a≠0)有两个相等的实数根。
7. 抛物线y= ax2+bx+c(a≠0)与x轴无交点,则一元二次方程ax2+bx+c=0(a≠0) 实数根。
2011年中考题组
一、选择题(每小题3分,共30分)
1.如果y=(m-2)x是关于x的二次函数,则m=( )
A.-1 B.2 C.-1或2 D.m不存在
2.对于抛物线y=x2+2和y=x2的论断:①开口方向相同;②形状完全相同;③对称轴相同.其中正确的有( )
A.0个 B.1个 C.2个 D.3个
3.y=x2-7x-5与y轴的交点坐标为( )
A.-5 B.(0,-5) C.(-5,0) D.(0,-20)
4.下列函数一定是关于x的二次函数的是( )
A.y=ax+bx+c B.y=x+bx+c
C.y=(a2+a)x2+bx+c D.y=(a2-a)x2+bx+c
5.下列函数关系中,可以看作二次函数y=ax2+bx+c(a≠0)模型的是( )
A.在一定距离内,汽车行驶的速度与行驶的时间的关系
B.我国人口的自然增长率为1%,这样我国总人口数随年份变化的关系
C.矩形周长一定时,矩形面积和矩形边长之间的关系
D.圆的周长与半径之间的关系
6.二次函数y=x2-2x-1的顶点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.抛物线y=x2-x-6与x轴的交点坐标是( )
A.(3,0) B.(-2,0) C.(-6,0),(1,0) D.(3,0),(-2,0)
8.已知一次函数y=ax+c与二次函数y=ax2+bx+c,它们在同一坐标系内的大致图象是( )
9.下列关于抛物线y=x2+2x+1的说法中,正确的是( )
A.开口向下 B.对称轴是直线x=1
C.与x轴有两个交点 D.顶点坐标是(-1,0)
10.下列函数中,二次函数是( )
A.y=8x2+1 B.y=8x+1 C.y= HYPERLINK "http://" +1
11、设抛物线y=x2+8x-k的顶点在x轴上,则k的值为( )
A -16 B 16 C -8 D 8
12、下列函数中,当x<0时,y随x的增大而减小的函数是( )
A y=-3x B y=4x C D y=-x2
二、填空题(每小题3分,共30分) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
13.抛物线y=2x2-6x-1的顶点坐标为_______,对称轴为________.
14.二次函数y=ax2-bx+c的图象如图1所示,则a,b,c与零的大小关系为a____0,b_____0,c_____0.
( http: / / )
(1) (2)
15.若抛物线y=(m-1)x2+2mx+2m-1的图象的最低点的纵坐标为零,则m=_____.
16.已知二次函数y=ax2-4x-13a有最小值-17,则a=______.
17.二次函数y=x2+2的图象开口_______,对称轴是______,顶点坐标是_______.
18.如图2,用长60米的篱笆,靠墙围成一个长方形场地,在表示场地面积时,可以设_______为x米,也可以选择_______为x米,相应地面积S的解析式为_____或______.
19.抛物线y=x2+2x+4的图象可以看作是将y=x的图象经过_________平移得到的.
20.使函数y=x2-3x+2的值为零的x的值为_______.
21.函数y=2-3x2的图象,开口方向是________,对称轴是________,顶点坐标是_________.
22.无论m为任何实数,总在抛物线y=x2+2mx+m上的点是________.
三、解答下列各题(每题8分,共40分) ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
23.已知抛物线y=x2-2ax+2a+b在x轴上截得的线段长为3,并且此抛物线的顶点坐标满足关系式:y=-x2,求a、b的值.
24.已知:如图所示,在△ABC中,BC=20,高AD=16,内接矩形EFGH的顶点E、F在BC上,G、H分别在AC、AB上,求内接矩形EFGH的最大面积.
25.已知正方形ABCD的边长为4,E为AB边上的一动点,(E与A,B点不重合),设AE=x,以E为顶点的内接正方形的面积为y,求y与x的函数关系式,当x为何值时,内接正方形的面积最小?
26.已知一个二次函数y=ax2+bx+c的图象如图所示,请求出这个二次函数的关系式.
( http: / / )
27.某商店经营一种水产品,成本为每千克40元,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,针对这种水产品的销售情况,请回答下列问题:
(1)当销售单价为每千克55元时,计算销售量和月利润.
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式.
(3)销售单价定为多少元时,获得的利润最多?
28、已知抛物线的顶点为(1,-1),且过点(2,1),求这个函数的表达
29、已知一个二次函数的图象经过点(1,-1),(0,1),(-1,13),求这个二次函数的解析式;
30、已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上, 分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
(1)用含y的代数式表示AE.
(2)求y与x之间的函数关系式,并求出x的取值范围.
(3)设四边形DECF的面积为S,求出S的最大值.
标准答案
1.A 解析:令m2-m=2,解得m=2或m=-1,而m=2不合适,舍去.
2.D
3.B 解析:令x=0,求出y的值为-5.
4.B 5.C
6.D 解析:将二次函数进行配方为y=(x-1)2-2,顶点坐标为(1,-2).
7.D 解析:令y=0,求出x的值为-2与3,故交点坐标为(3,0),(-2,0).
8.C 9.D
10.A 解析:紧扣定义中的形式,B为一次函数,C为反比例函数,D虽是函数,但不是二次函数.11、A 12、A
13.(,-) x= 解析:将y=2x-6x-1配方为y=2(x- HYPERLINK "http://" )2-.
14.> < < 15. 16.1, 17.向上 y轴 (0,2)
18.AB BC S=-2x2+60x或S=-x2+30x
19.向左平移1个单位,再向上平移3个单位
20.1,2 21.向下 y轴 (0,2)
22.(,) 解:将y=x2+2mx+m进行整理得到y=x2+(2x+1)m,为使不受m的限制, 令2x+1=0,得出x=-,从而y=.
23.解:由题意知,抛物线的对称轴为x= HYPERLINK "http://" =a,
抛物线与x轴交点的横坐标为a-,a+.
抛物线的解析式也可以写成y=[x-(a-)][x-(a+)]=x2-2ax+a2-,
所以a2-=2a+b,令x=a,则y=- HYPERLINK "http://" ,所以顶点坐标为(a,-).
由于顶点坐标满足y=-x2,所以-=-a2,
故a=±,又2a+b=a2-=0,所以b=-2a,
所以a=,b=-3;或a=-,b=3.
24.80
25.y=2x2-8x+16.当x=2时,内接正方形的面积最小.
26.y=-x2+ HYPERLINK "http://" x+1
27.(1)450千克,6 750元;
(2)y=-10x2+1 400x-40 000;
(3)销售单价定为70元时,获得的利润最多是9 000元. ( http: / / www.21cnjy.com / " \o "欢迎登陆21世纪教育网 )
30、(1)由已知得DECF是矩形,故EC=DF=y,AE=8-EC=8-y.
(2)∵DE∥BC,∴△ADE∽△ABC,∴,即.
∴y=8-2x(0
C
B
F
E
A
