小升初数学全能解法及训练课件 数列求和(15张PPT)
文档属性
| 名称 | 小升初数学全能解法及训练课件 数列求和(15张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 20:39:29 | ||
图片预览





文档简介
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
解法精讲
Knowledge network
01
典型例题
Question type analysis
02
举一反三
Real exercise
03
知识小结
Knowledge summary
04
解法精讲
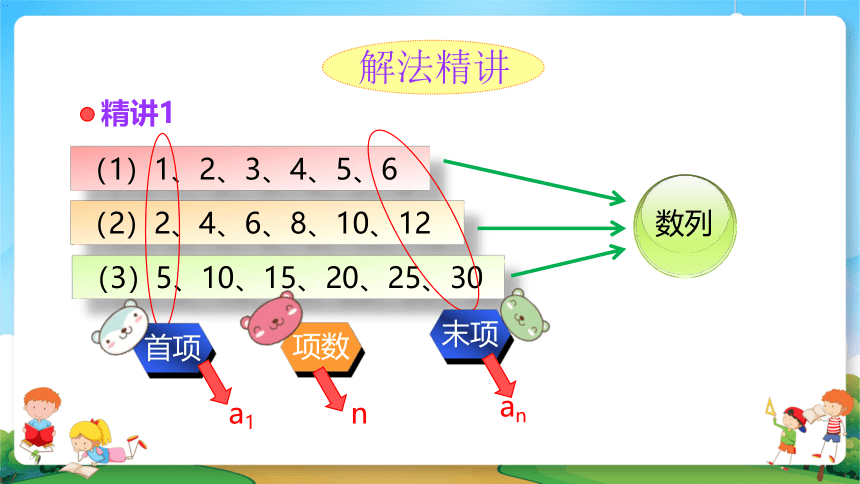
精讲1
(1)1、2、3、4、5、6
(2)2、4、6、8、10、12
(3)5、10、15、20、25、30
数列
首项
末项
项数
a1
an
n
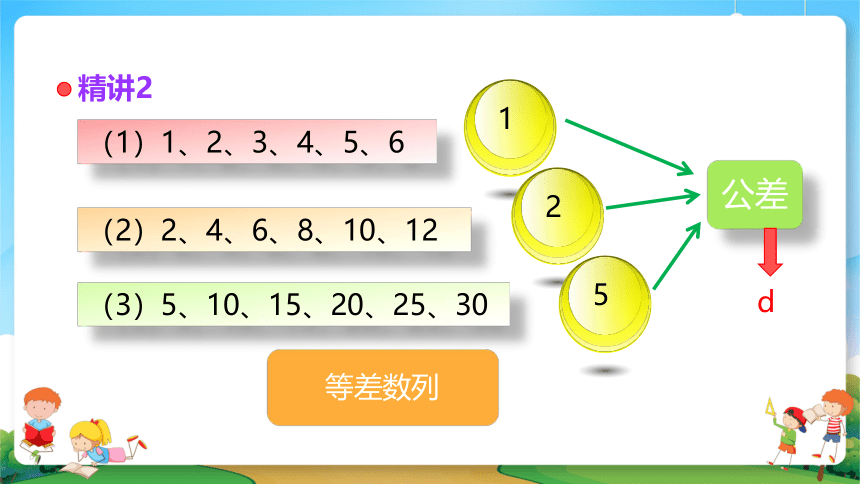
精讲2
(1)1、2、3、4、5、6
(2)2、4、6、8、10、12
(3)5、10、15、20、25、30
1
2
5
公差
等差数列
d
精讲3
数列:1、3、5、7、9、11……
首项+公差×(2-1)
第3项: 5=1+2 ×2
第4项: 7=1+2 ×3
第2项: 3=1+2
首项+公差×(3-1)
首项+公差×(4-1)
an=a1+(n-1)×d
精讲4
数列:6 、10 、14 、18 、22 、26 30 、34 、38
数列的和
6 + 10 + 14 + 18 + 22 + 26 + 30 + 34 + 38
38+ 34 + 30 + 26 + 22 + 18 + 14 + 10 + 6
44 44 44 44 44 44 44 44 44
(6+38)×9÷2
=198
S=(a1+an)n÷2
典例精析
例1
有一个数列:4、10、16、22······52,这个数列
共有多少项?
an=a1+(n-1)×d
n=(an-a1)÷d+1
等差
数列
典例精析
例1
有一个数列:4、10、16、22······52,这个数列
共有多少项?
(52-4)÷6+1
=48÷6+1
=8+1
=9(项)
答:这个数列共有9项。
例2
求数列2+4+6+······+2000的和。
S=(a1+an)n÷2
n=(an-a1)÷d+1
等差数列
例2
求数列2+4+6+······+2000的和。
n=(2000-2)÷2+1
=1998÷2+1
=999+1
=1000
S=(2000+2)×1000÷2
=2002×1000÷2
=2002000÷2
=1001000
举一反三
练习1
有一数列:101,203,105,207,109,211…
求这数列的前20项的和。
(101+137)×10÷2=1190
(203+239)×10÷2=2210
前20项的和是:
1190+2210=3400
奇数项一列,偶数
项一列;据等差数列求和
公式求解。
规律总结
+
练习2
求7800-124-128-132···-272-276的差。
124+128 + 132··· + 272 + 276
=(124+276)×39÷2
=7800
7800-7800=0
先运用等差公式
求出和,再用7800相减。
规律总结
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
2021/小升初数学/总复习/专题复习/教学课件
解法精讲
Knowledge network
01
典型例题
Question type analysis
02
举一反三
Real exercise
03
知识小结
Knowledge summary
04
解法精讲
精讲1
(1)1、2、3、4、5、6
(2)2、4、6、8、10、12
(3)5、10、15、20、25、30
数列
首项
末项
项数
a1
an
n
精讲2
(1)1、2、3、4、5、6
(2)2、4、6、8、10、12
(3)5、10、15、20、25、30
1
2
5
公差
等差数列
d
精讲3
数列:1、3、5、7、9、11……
首项+公差×(2-1)
第3项: 5=1+2 ×2
第4项: 7=1+2 ×3
第2项: 3=1+2
首项+公差×(3-1)
首项+公差×(4-1)
an=a1+(n-1)×d
精讲4
数列:6 、10 、14 、18 、22 、26 30 、34 、38
数列的和
6 + 10 + 14 + 18 + 22 + 26 + 30 + 34 + 38
38+ 34 + 30 + 26 + 22 + 18 + 14 + 10 + 6
44 44 44 44 44 44 44 44 44
(6+38)×9÷2
=198
S=(a1+an)n÷2
典例精析
例1
有一个数列:4、10、16、22······52,这个数列
共有多少项?
an=a1+(n-1)×d
n=(an-a1)÷d+1
等差
数列
典例精析
例1
有一个数列:4、10、16、22······52,这个数列
共有多少项?
(52-4)÷6+1
=48÷6+1
=8+1
=9(项)
答:这个数列共有9项。
例2
求数列2+4+6+······+2000的和。
S=(a1+an)n÷2
n=(an-a1)÷d+1
等差数列
例2
求数列2+4+6+······+2000的和。
n=(2000-2)÷2+1
=1998÷2+1
=999+1
=1000
S=(2000+2)×1000÷2
=2002×1000÷2
=2002000÷2
=1001000
举一反三
练习1
有一数列:101,203,105,207,109,211…
求这数列的前20项的和。
(101+137)×10÷2=1190
(203+239)×10÷2=2210
前20项的和是:
1190+2210=3400
奇数项一列,偶数
项一列;据等差数列求和
公式求解。
规律总结
+
练习2
求7800-124-128-132···-272-276的差。
124+128 + 132··· + 272 + 276
=(124+276)×39÷2
=7800
7800-7800=0
先运用等差公式
求出和,再用7800相减。
规律总结
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
同课章节目录
