小升初数学全能解法及训练课件 质数与合数(18张PPT)
文档属性
| 名称 | 小升初数学全能解法及训练课件 质数与合数(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 6.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-27 20:59:55 | ||
图片预览


文档简介
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
解法精讲
Knowledge network
01
典型例题
Question type analysis
02
举一反三
Real exercise
03
知识小结
Knowledge summary
04
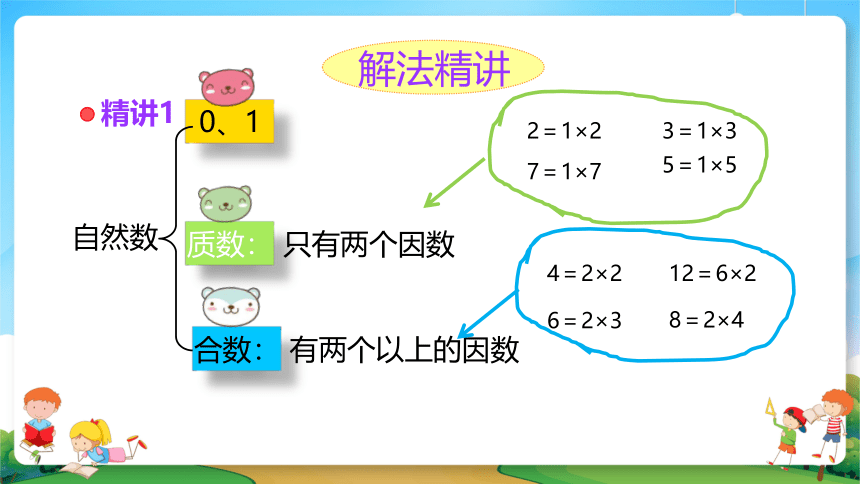
解法精讲
精讲1
自然数
0、1
质数:
只有两个因数
合数:
有两个以上的因数
2=1×2
3=1×3
7=1×7
6=2×3
4=2×2
5=1×5
12=6×2
8=2×4
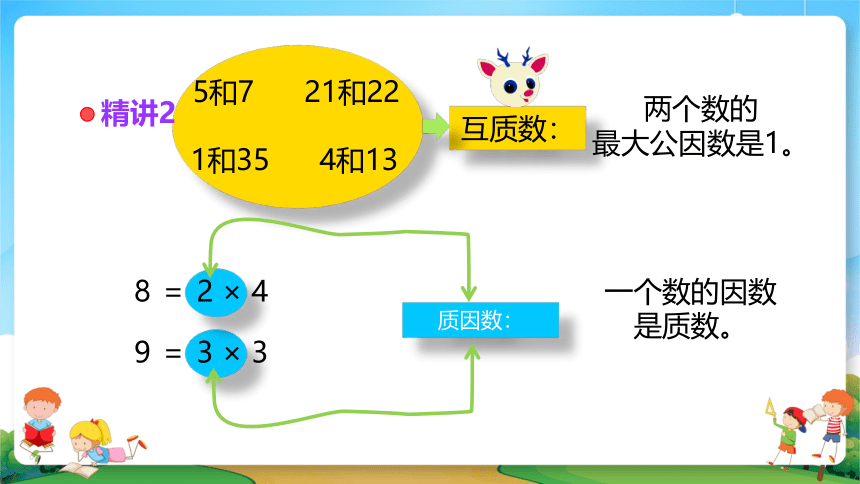
精讲2
质因数:
一个数的因数
是质数。
8 = 2 × 4
互质数:
两个数的
最大公因数是1。
5和7
4和13
21和22
1和35
9 = 3 × 3
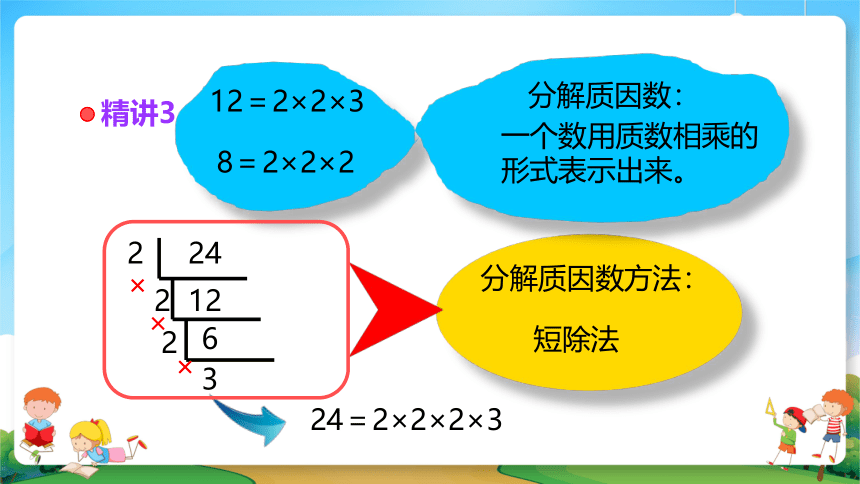
分解质因数方法:
短除法
24
2
12
2
6
2
3
×
×
24=2×2×2×3
×
分解质因数:
一个数用质数相乘的
形式表示出来。
12=2×2×3
8=2×2×2
精讲3
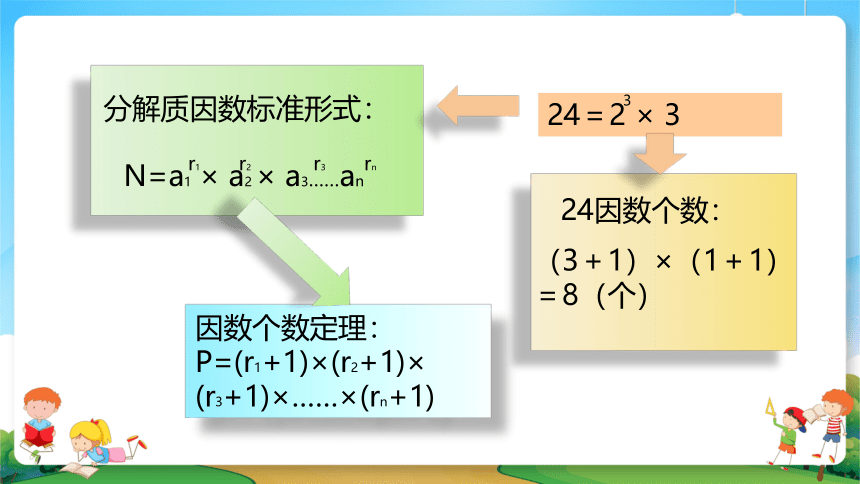
24因数个数:
分解质因数标准形式:
N=a1 × a2 × a3……an
r1
r2
r3
rn
因数个数定理:
P=(r1+1)×(r2+1)×
(r3+1)×……×(rn+1)
(3+1)×(1+1)
=8(个)
质数与全数
2是质偶数
一个特殊数
熟记100以内
的质数表
一张质数表
和差积商的
奇偶性
一种性质
典例精析
例1
两个质数的和是81,这两个质数的积是多少?
偶数+奇数
=奇数
2即是偶数,
又是质数。
典例精析
例1
两个质数的和是81,这两个质数的积是多少?
81-2=79
79×2=158
答:这两个质数的积是158。
例2
两个质数的和是60,两个质数积的最大值是多少?
例2
两个质数的和是60,两个质数积的最大值是多少?
60=7+53=13+47=19+41=23+37=29+31
7×53=371
13×47=611
19×41=119
23×37=851
29×31=899
答:两个质数积的最大值是899。
例3
240有多少个因数?
分解质因数
标准形式:
因数个数定理
例3
240有多少个因数?
240=2 × 3 × 5
4
1
1
(4+1)×(1+1)×(1+1)=20(个)
答:240有20个因数。
练习1
筐里有96个苹果,,如果不一次拿出,也没一个个
地拿,要求每次拿出的个数相同,拿完时,又正好
不多少,有多少种不同的拿法?
此题实际求96的因数个数,根据因数个数定理求解。
举一反三
96=2 × 3
5
(5+1)×(1+1)=12
12-2=10(种)
参考
答案
练习2
有7个不同的质数,它们的和是60,其中最小的质数是多少?
其中六个质数的和是偶数。
60-偶数=偶数
即第七个质数是偶数。
所以最小的质数是2。
参考
答案
2是唯一的质偶数,是解决质数与合数问题的突破口
规律总结
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
2021/小升初数学/总复习/专题复习/教学课件
解法精讲
Knowledge network
01
典型例题
Question type analysis
02
举一反三
Real exercise
03
知识小结
Knowledge summary
04
解法精讲
精讲1
自然数
0、1
质数:
只有两个因数
合数:
有两个以上的因数
2=1×2
3=1×3
7=1×7
6=2×3
4=2×2
5=1×5
12=6×2
8=2×4
精讲2
质因数:
一个数的因数
是质数。
8 = 2 × 4
互质数:
两个数的
最大公因数是1。
5和7
4和13
21和22
1和35
9 = 3 × 3
分解质因数方法:
短除法
24
2
12
2
6
2
3
×
×
24=2×2×2×3
×
分解质因数:
一个数用质数相乘的
形式表示出来。
12=2×2×3
8=2×2×2
精讲3
24因数个数:
分解质因数标准形式:
N=a1 × a2 × a3……an
r1
r2
r3
rn
因数个数定理:
P=(r1+1)×(r2+1)×
(r3+1)×……×(rn+1)
(3+1)×(1+1)
=8(个)
质数与全数
2是质偶数
一个特殊数
熟记100以内
的质数表
一张质数表
和差积商的
奇偶性
一种性质
典例精析
例1
两个质数的和是81,这两个质数的积是多少?
偶数+奇数
=奇数
2即是偶数,
又是质数。
典例精析
例1
两个质数的和是81,这两个质数的积是多少?
81-2=79
79×2=158
答:这两个质数的积是158。
例2
两个质数的和是60,两个质数积的最大值是多少?
例2
两个质数的和是60,两个质数积的最大值是多少?
60=7+53=13+47=19+41=23+37=29+31
7×53=371
13×47=611
19×41=119
23×37=851
29×31=899
答:两个质数积的最大值是899。
例3
240有多少个因数?
分解质因数
标准形式:
因数个数定理
例3
240有多少个因数?
240=2 × 3 × 5
4
1
1
(4+1)×(1+1)×(1+1)=20(个)
答:240有20个因数。
练习1
筐里有96个苹果,,如果不一次拿出,也没一个个
地拿,要求每次拿出的个数相同,拿完时,又正好
不多少,有多少种不同的拿法?
此题实际求96的因数个数,根据因数个数定理求解。
举一反三
96=2 × 3
5
(5+1)×(1+1)=12
12-2=10(种)
参考
答案
练习2
有7个不同的质数,它们的和是60,其中最小的质数是多少?
其中六个质数的和是偶数。
60-偶数=偶数
即第七个质数是偶数。
所以最小的质数是2。
参考
答案
2是唯一的质偶数,是解决质数与合数问题的突破口
规律总结
主讲教师:数学老师
2021/小升初数学/总复习/专题复习/教学课件
谢谢观赏
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
同课章节目录
